Đề giữa học kì 1 Toán 8 năm 2025 – 2026 trường THCS Tân Sỏi – Bắc Ninh

UBND XÃ YÊN THẾ
ĐỀ KIỂM TRA ĐÁNH GIÁ GIỮA HỌC KỲ I
TRƯỜNG THCS TÂN SỎI NĂM HỌC 2025 - 2026 MÔN: Toán 8
Thời gian làm bài: 90 phút, không kể thời gian giao đề
I. MA TRẬN ĐỀ KIỂM TRA
Mức độ đánh giá Tổng % điểm TT Chương/Chủ đề
Nội dung/đơn vị kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TNKQ TL TNKQ TL TNKQ TL TNKQ TL
Đa thức nhiều biến. Các Câu 1 Câu 2 Câu 2 Biểu thức
phép toán cộng, trừ, nhân, 7 câu a,b 1 câu a b 45% đại số
chia các đa thức nhiều biến 1 1,75đ 1đ 0,25đ 0,75 đ 0,75 đ
Hằng đẳng thức đáng nhớ 3 câu Câu 1 1 câu 0,75đ c 0,5đ 17,5% 0,5 đ 2 Định lí Định lí Pythagore 1 câu Pythagore 0,25đ 2,5% 3 Tính chất và dấu hiệu 5 câu 2 câu Câu 3 1 câu Câu 3 Tứ giác
nhậnbiết các tứ giác đặc biệt a b 35% 1,25đ 0,5đ 1đ 0,25đ 0,5đ Tổng: Số câu
16 câu 1 câu 3 câu 3 câu 2 câu 1câu 26 câu Điểm 4,0 đ 1đ 0,75đ 2,25đ 1,25đ 0,5đ 10 điểm Tỉ lệ % 50% 30% 15% 5% 100% Tỉ lệ chung 80% 20% 100%
II. ĐẶC TẢ ĐỀ KIỂM TRA
Số câu/ý hỏi theo mức độ nhận TT Chương/ Nội dung/Đơn vị thức Chủ đề kiến thức
Mức độ đánh giá NB TH VD VD cao
Nhận biết: Nhận biết được các khái 7TN
niệm về đơn thức, đa thức nhiều biến, đa thức thu gọn
Thông hiểu: Tính được giá trị của đa 1 Biểu thức
Đa thức nhiều biến. thức khi biết giá trị của các biến. 1TN, 1TL đại số
Các phép toán Vận dụng:
cộng, trừ, nhân,
– Thực hiện được việc thu gọn đơn 1TL
chia các đa thức thức, đa thức. nhiều biến
– Thực hiện được phép nhân đơn thức
với đa thức và phép chia hết một đơn
thức cho một đơn thức.
– Thực hiện được các phép tính: phép
cộng, phép trừ, phép nhân các đa thức
nhiều biến trong những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa
thức cho một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: Nhận biết được các khái 1 TN nhớ
niệm: đồng nhất thức, hằng đẳng thức.
Thông hiểu: Mô tả được các hằng đẳng 1TL
thức: bình phương của tổng và hiệu;
hiệu hai bình phương, lập phương của
một tổng và hiệu; tổng và hiệu hai lập phương.
Vận dụng cao: Vận dụng được hằng 1 TL
đẳng thức để tính giá trị biểu thức Định lí
Nhận biết: Nhận biết được tam giác là 1TN Pythagore
tam giác vuông khi biết độ dài 3 2 Định lí Pythagore cạnh của một tam giác.
Nhận biết: Nhận biết được dấu hiệu 5TN
để một hình thang là hình thang cân;
một tứ giác là hình bình hành; một
hình bình hành là hình chữ nhật; hình
bình hành là hình thoi; hình chữ nhật
Định nghĩa, Tính chất và là hình vuông. Thông hiểu: 2TN,1TL 3 Tứ giác
dấu hiệu nhậnbiết các tứ Áp dụng kiến thức nhận biết được một
giác đặc biệt
tứ giác có là hình thang vuông.
Vận dụng: Vận dụng định nghĩa, tính 1TN, 1TL
chất và dấu hiệu nhận biết hình bình
hành vào giải toán UBND XÃ YÊN THẾ
ĐỀ KIỂM TRA ĐÁNH GIÁ GIỮA HỌC KỲ I
TRƯỜNG THCS TÂN SỎI NĂM HỌC 2025 - 2026 MÔN: Toán 8 (Đề gồm 03 trang)
Thời gian làm bài: 90 phút, không kể thời gian giao đề
PHẦN I. TRẮC NGHIỆM (5,0 điểm)
Hãy lựa chọn chữ cái in hoa đứng trước câu trả lời đúng và ghi ra tờ giấy thi.
Câu 1: Trong các biểu thức sau , đơn thức nhiều biến là?
A. 2x − 2x +1. B. 2
− y + 5y + 2 . C. 2
12x + y . D. 2 4a .5b
Câu 2: Với A, B bất kỳ, khẳng định nào sau đây là đúng? A. 2 2 3
(A − B) = A − 2AB − B . B. 2 2 2
(A + B) = A + B C. 3 3 3
(A − B) = A − B D. 3 3 2 2 3
(A + B) = A + 3A B + 3AB + B .
Câu 3: Khẳng định nào sau đây là sai ?
A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.
B. Hình bình hành có hai góc đối bằng nhau.
C. Hình bình hành có hai đường chéo vuông góc với nhau.
D. Hình bình hành có hai cặp cạnh đối song song
Câu 4. Bậc của đơn thức 2 2 2 2
− x y z là: A. 5 B. 6 C. 7 D. 4
Câu 5: Tổng số đo các góc trong một tứ giác bằng : A. 3600 B. 1000 C. 1800 D. 900
Câu 6: Khai triển biểu thức (x + )3
1 ta được kết quả là: A. 3 2
x − 3x + 3x −1. B. 3 2
x + 3x + 3x +1 C. 3 2
x + 9x + 3x +1. D. 3 2
x − 9x + 3x −1.
Câu 7: Bậc của đa thức 5 2 2 5 3 2
P = 2x − x y − 2x + x − xy − 2025 bằng A. 5 B. 4 C. 3 D. 2
Câu 8: Đơn thức 3 2
9x yz chia hết cho đơn thức nào sau đây? A. 4 2 3x yz B. 3 2 5x y z C. 3 3 4 − x yz . D. 3 2 − x z
Câu 9: Chọn phương án sai trong các phương án sau:
A. Tứ giác có hai cạnh đối song song là hình thang
B. Hình thang có hai góc kề một đáy bằng nhau là hình thang cân
C. Hình thang cân có hai cạnh bên bằng nhau
D. Hình thang có hai cạnh bên bằng nhau là hình thang cân
Câu 10: Kết quả của phép tính (x + y)2 – (x – y)2 bằng: A. 2x2 B. 2y2 C. 4xy D. 0
Câu 11: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau: A. 3cm; 4cm; 5cm B. 6cm; 8cm; 9cm C. 2cm; 4cm; 5cm D. 5cm; 5cm; 7cm
Câu 12: Kết quả của phép nhân ( 2x2 -3yz + 4xy2).( -3xy) bằng :
A. 6x3y +9xy2z -12 x2y2
B. -6x3y +9xy2z -12 x2y3
C. 6x3y - 9xy2z -12 x2y2
D. 6x3y +9xy2z +12 x2y2
Câu 13: Trong các đơn thức sau, đơn thức nào đồng dạng với đơn thức 2 3 − x y ? . A. 2 1 − 2xy .
B. 3x .y . C. 2 x . y 3 . D. 2 2 3x y .
Câu 14: Ta có 2x + 6xy +... = (x +3y)2 thì đơn thức phải điền vào chỗ chấm là: A. 9y B. 2 4x C. 2 12x D. ( )2 3y
Câu 15: Hình bình hành ABCD có O là giao điểm của AC và BD. Biết OC = 3cm,
khẳng định nào là đúng?
A. BD = 6cm. B. OB = 3cm. C. OA = 6cm.
D. AC = 6cm .
Câu 16: Hình vuông có đường chéo bằng 4cm thì cạnh của nó bằng A. 2cm B. 8cm C. 8 c . m D. 4cm
Câu 17: Giá trị của đơn thức 2 2 3
2x y z tại x = 1, − y = 1, − z = 2 − là: A. 12 B. - 16 C. 16 D. - 12
Câu 18: Cho hình thang cân ABCD (AB// CD) có  0 D = 80 . Tìm  ABC A. 110o B. 80o C. 90o D. 100o Câu 19: Cho hình chữ nhật ABCD có AB = 8c ,
m BC = 6cm . Các điểm M,N,P,Q là A M B
trung điểm của các cạnh hình chữ nhật.
Tổng diện tích các tam giác trong hình bên Q N là: A. 2 24cm B. 2 6cm D C. C 2 12cm D. 2 4cm P
Câu 20: Tứ giác nào sau đây vừa là hình chữ nhật, vừa là hình thoi? A. Hình chữ nhật. B. Hình thang.
C. Hình vuông . D. Hình thoi.
PHẦN II. TỰ LUẬN (5,0 điểm). Câu 1. (1,5 điểm)
1. Thực hiện phép tính: a) x(xy - 2) b) ( 3 3 2 2
3x y − 6x y −12xy):3xy . 2. Tính nhanh 2 99 + 2.99 +1 Câu 2. (1,5 điểm) 1. Tìm đa thức A biết :
A + (x3 – xyz + 3xz2 ) = y 3 – xyz - 3xz2.
2. Rút gọn biểu thức: B = (x + )2
1 − (x − 2)(x + 2) Câu 3. (1,5 điểm)
Cho tam giác ABC vuông tại A, đường cao AH. Từ H kẻ HD vuông góc với AB, HE vuông góc với AC.
a. Chứng minh tứ giác ADHE là hình chữ nhật.
b. Gọi O là trung điểm của HC. Trên tia đối của tia OA lấy điểm G sao cho O là trung
của AG. Chứng minh ba điểm D, H, G thẳng hàng. Câu 4. (0,5 điểm)
Cho các số x, y thoả mãn 2 2
x + y − 3x − 3y + xy + 3 = 0 . Tính giá trị của biểu thức: 2024 2025 2026
Q = (x − y) + (x − 2) + y .
--------------------------------Hết-------------------------------
Họ và tên học sinh:........................................................................Số báo danh:.............. UBND XÃ YÊN THẾ HƯỚNG DẪN CHẤM
TRƯỜNG THCS TÂN SỎI
ĐỀ KIỂM TRA ĐÁNH GIÁ GIỮA HỌC KÌ I NĂM HỌC 2025-2026 MÔN: TOÁN LỚP 8
I. TRẮC NGHIỆM (5 điểm): Mỗi câu đúng 0,25 điểm Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án 1 D 6 B 11 A 16 C 2 D 7 B 12 B 17 B 3 C 8 D 13 C 18 D 4 A 9 D 14 D 19 A 5 A 10 C 15 D 20 C
II. TỰ LUẬN (5 điểm) Câu
Sơ lược các bước giải Điểm Bài 1. (1,5 điểm)
Câu 1 1. Thực hiện phép tính: a) x(xy - 2) b) ( 3 3 2 2
3x y − 6x y −12xy):3xy . 2. Tính nhanh: 2 99 + 2.99 +1 a) 2 x(xy - 2) = .
x xy - 2x = x y - 2x 0,5đ 1.a,b b) (1,0đ) ( 3 3 2 2 x y x y xy) xy = ( 3 3 x y xy) + ( 2 2 3 - 6 -12 :3 3 :3 6
− x y :3xy) + (-12xy :3xy) 0,25đ = 2 2
x y − 2xy − 4 0,25đ 2. Ta có: + + = + + = ( + )2 2 2 2 99 2.99 1 99 2.99.1 1 99 1 0,25đ (0,5đ) 2 = (100) = 10000 0,25đ Bài 2. (1,5 điểm)
1.Tìm đa thức A, biết
Câu 2 A + (x3 – xyz + 3xz2 ) = y 3 – xyz - 3xz2.
2. Rút gọn biểu thức: B = (x + )2
1 − (x − 2)(x + 2) .
𝐴𝐴 + (𝑥𝑥3 − 𝑥𝑥𝑥𝑥𝑥𝑥 + 3𝑥𝑥𝑥𝑥2) = 𝑥𝑥3 − 𝑥𝑥𝑥𝑥𝑥𝑥 − 3𝑥𝑥𝑥𝑥2. 0,25đ 1.
A = 𝑥𝑥3 − 𝑥𝑥𝑥𝑥𝑥𝑥 − 3𝑥𝑥𝑥𝑥2 − 𝑥𝑥3 + 𝑥𝑥𝑥𝑥𝑥𝑥 − 3𝑥𝑥𝑥𝑥2
(0,75đ) A = 𝑥𝑥3 − 6𝑥𝑥𝑥𝑥2 − 𝑥𝑥3 0,25đ
Vậy: A = 𝑥𝑥3 − 6𝑥𝑥𝑥𝑥2 − 𝑥𝑥3 0.25đ
B = (x + )2 − (x − )(x + ) = ( 2
x + x + ) − ( 2 2 1 2 2 2 1 x − 2 ) 0.25đ 2. 2 2
= x + 2x + 1 − x + 4 (0,75đ) = 2x + 5 0.25đ Vậy: B = 2x + 5 0.25đ Bài 3. (1,5 điểm)
Cho tam giác ABC vuông tại A, đường cao AH. Từ H kẻ HD vuông
Câu 3 góc với AB, HE vuông góc với AC.
a. Chứng minh tứ giác ADHE là hình chữ nhật.
b. Gọi O là trung điểm của HC. Trên tia đối của tia OA lấy điểm G sao
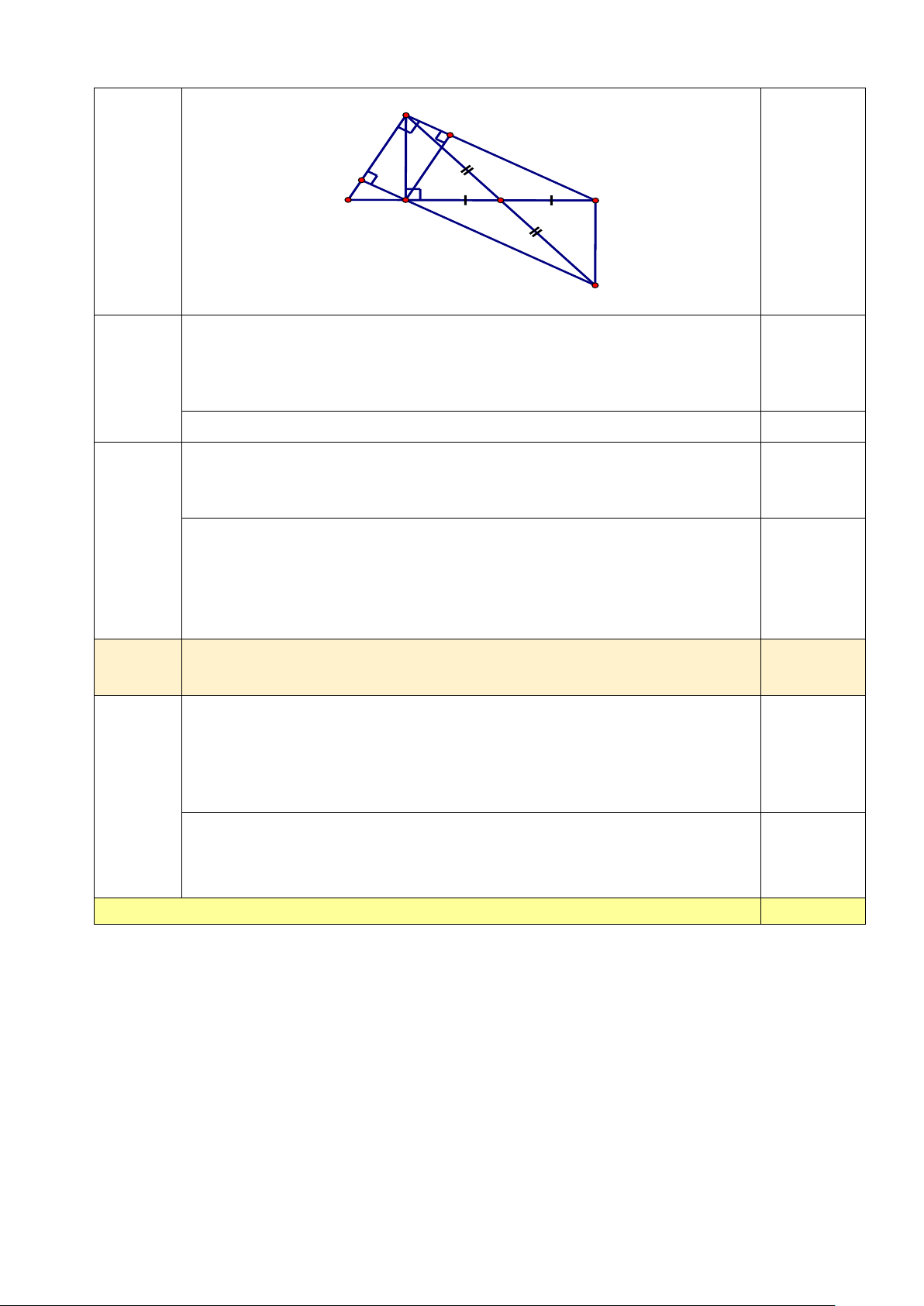
cho O là trung của AG. Chứng minh ba điểm D, H, G thẳng hàng. A E D B H O C G
a) Xét tứ giác ADHE có  90o DAE = (do ABC ∆ vuông tại A) 0,25đ 0,25đ
(1,0đ)  90o ADH =
(do HD ⊥ AB tại D)  90o AEH =
(do HE ⊥ AC tại E) 0,25đ
Suy ra tứ giác ADHE là hình chữ nhật (dấu hiệu nhận biết) 0,25đ
b) Từ giác AHGC có 2 đường chéo AG và HC cắt nhau tại O mà O lại
là trung điểm của AG và HC (theo đầu bài). Do đó, tứ giác AHGC là 0.25
hình bình hành, suy ra AC // HG .
(0,5đ) Do AC // HG mà HE ⊥ AC suy ra EH ⊥ HG nên  90o EHG = . Do tứ
giác ADHE là hình chữ nhật nên  90o DHE = . 0,25đ
Ta có  +  = 90O + 90O =180O DHE EHG hay  180o DHG = , suy ra 3
điểm D, H, G thẳng hàng.
Cho các số x, y thoả mãn 2 2 + − − + + = . Tính giá trị của Câu 4. x
y 3x 3y xy 3 0 biểu thức 2024 2025 2026
Q = (x − y) + (x − 2) + y . Ta có 2 2
x + y − 3x − 3y + xy + 3 = 0 2 2
2x + 2y − 6x − 6y + 2xy + 6 = 0 0.25đ 2 2 2
(x + y − 2) + (x −1) + (y −1) = 0
(0,5đ) Từ đó suy ra x = y = 1
Thay x = y =1 vào biểu thức Q ta được 2024 2025 2026 Q = (1−1) + (1− 2) +1 = 0 + ( 1 − ) +1 = 0 0.25đ Vậy Q = 0.
TỔNG ĐIỂM TOÀN BÀI 10 điểm
………………….Hết………………….. Duyệt của BGH
Duyệt của tổ chuyên môn Giáo viên ra đề Đỗ Thị Duyên Nguyễn Thị Minh Lê Thị Quyên
Document Outline

• II. ĐẶC TẢ ĐỀ KIỂM TRA
• Câu 15: Hình bình hành ABCD có O là giao điểm của AC và BD. Biết , khẳng định nào là đúng?
• A. . B. . C. . D. .