Đề giữa học kì 2 Toán 8 năm 2023 – 2024 trường THCS Giảng Võ – Hà Nội
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề kiểm tra giữa học kì 2 môn Toán 8 năm học 2023 – 2024 trường THCS Giảng Võ, quận Ba Đình, thành phố Hà Nội; kỳ thi được diễn ra vào ngày 13 tháng 03 năm 2024. Đề thi gồm 2 trang giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!
Preview text:
ỦY BAN NHÂN DÂN QUẬN BA ĐÌNH
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TRƯỜNG THCS GIẢNG VÕ NĂM HỌC 2023-2024 Môn: Toán 8 (Ca chiều) ĐỀ CHÍNH THỨC Ngày kiểm tra: 13/3/2024
Thời gian làm bài: 90 phút
(Đề kiểm tra gồm 02 trang)
Phần I. Trắc nghiệm (2,5 điểm)
Chọn đáp án đúng rồi viết vào giấy kiểm tra (Ví dụ: 1-A). P 2y 1
Câu 1. Đa thức P thỏa mãn là: 2 6y 2y A. 2 6y 3y B. 2 6y 3y C. 2 6y 3y D. 2 6y 2y 2 x 8x 16
Câu 2. Rút gọn biểu thức được kết quả là: 16 4x x 4 x 4 x 4 x 4 A. B. C. D. 4 4 4 16 1 3
Câu 3. Tổng của hai phân thức và là: x 3 2 x 6x 9 x x x 6 4 A. B. C. D. 2 (x 3) 2 (x 3) 2 (x 3) 2 (x 3) 3 2 1
Câu 4. Thực hiện phép tính : được kết quả là: 2 x x x 3x 2 3x 2 5 1 A. B. C. D. x x x x 2 x 4 5x 2 Câu 5. Trong đẳng thức : M 4, M là đa thức: 4x x x 2 1 x x 2 A. B. C. D. 4 4 4 4
Câu 6. Một hình chữ nhật có diện tích 2
200cm và chiều dài là x cm. Biểu thức biểu thị chu
vi của hình chữ nhật là: 400 200 200 A. 400x B. C. 2 x D. 2 200x x x x Câu 7. Cho A BC đồng dạng với D
EF theo tỉ số đồng dạng là 2; D EF đồng dạng với
MNP theo tỉ số đồng dạng là 2. Biết A 30 , tính số đo M. A. M 30 B. M 60 C. M 120 D. M 15
Câu 8. Bộ ba số đo nào dưới đây là độ dài ba cạnh của một tam giác vuông? A. 3c m, 5 c m, 6 c m B. 2c m, 4 c m, 6 c m C. 5c m, 1 c m, 2 c m D. 5c m, 1 2c m, 1 3c m
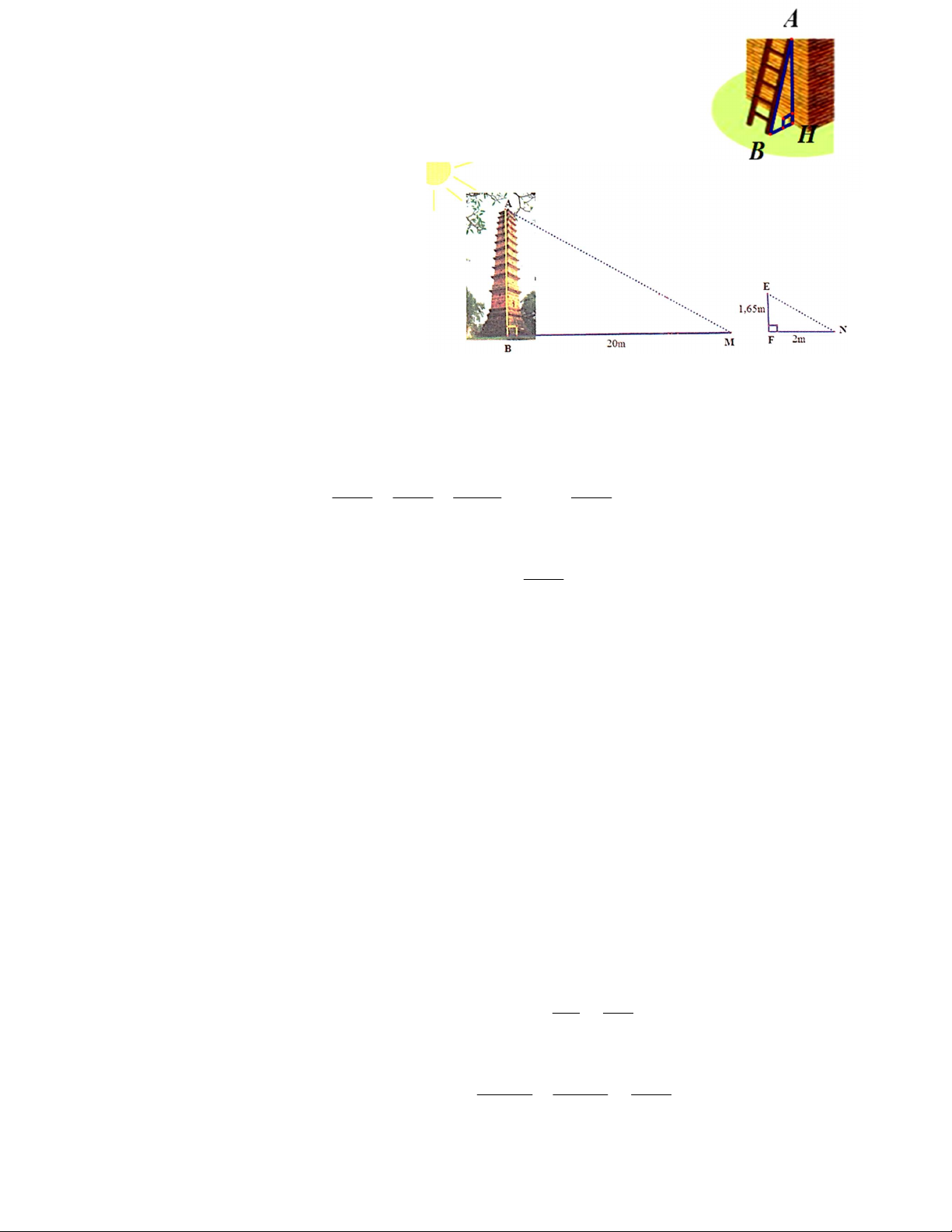
Câu 9. Một chiếc thang có chiều dài AB 2, 6m đặt cách một bức tường
khoảng cách BH như hình vẽ. Tính độ dài BH, nếu AH 2, 4m. A. 1m B. 0, 4m C. 2,4m D. 2m
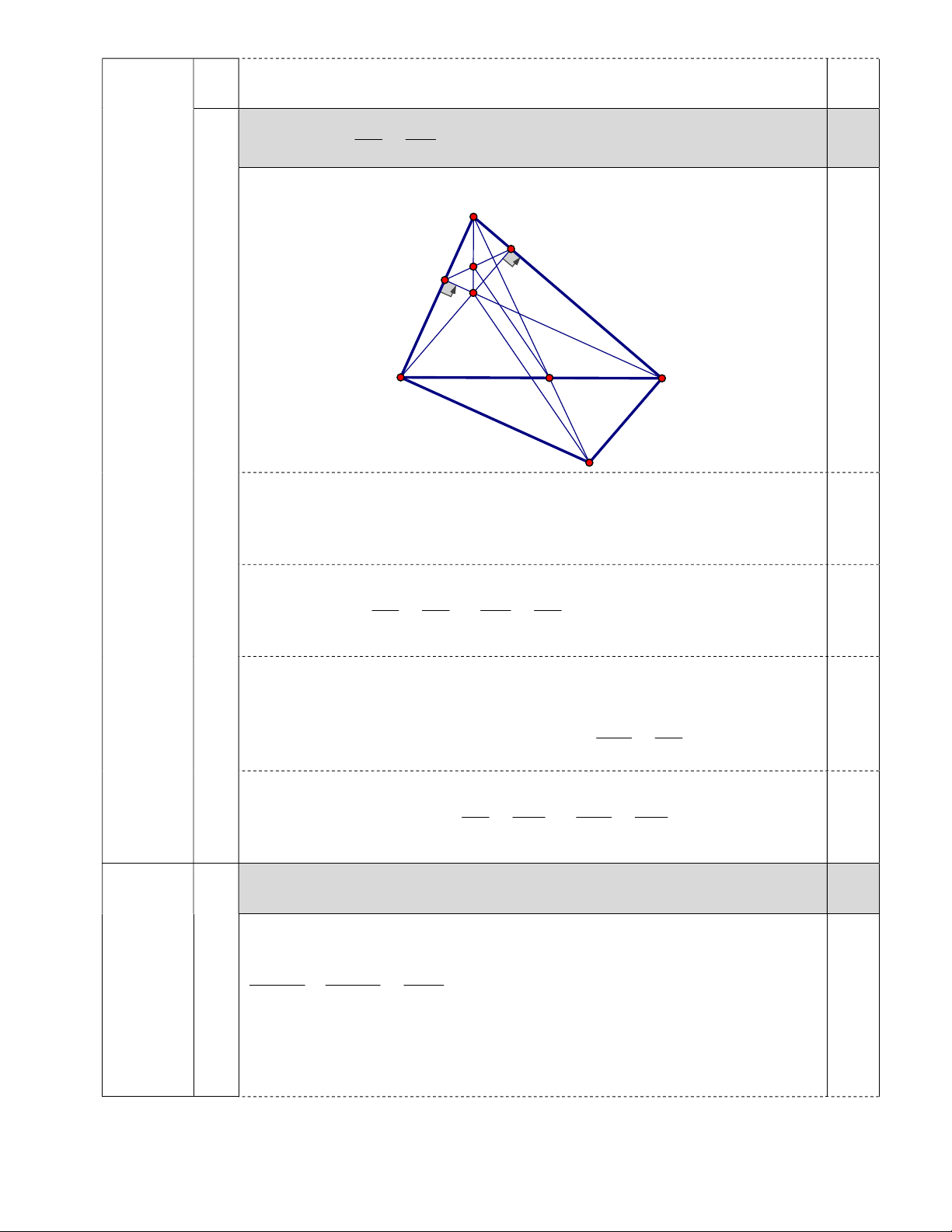
Câu 10. Bóng của tháp Bình Sơn
(Vĩnh Phúc) trên mặt đất có độ dài
20m được mô tả như hình vẽ. Cùng
thời điểm đó, một cột sắt EF cao
1,65m cắm vuông góc với mặt đất có
bóng dài 2m. Tính chiều cao của tháp,
biết tháp trên vuông góc với mặt đất và AM //EN. A. 33m B. 16, 5m C. 165m D. 8,25m
Phần II. Tự luận (7,5 điểm)
Học sinh trình bày lời giải vào giấy kiểm tra. Bài 1 (2,0 điểm) 2 x 1 x 2 x 2 Cho hai biểu thức A và B với x 2 , x 0. 2 x 2 x 2 x 4 x
a) Tính giá trị của biểu thức B tại x 3. 3
b) Cho biểu thức M A B. Chứng minh M . x 2
c) Tìm tất cả giá trị nguyên của x để biểu thức M nhận giá trị nguyên. Bài 2 (2,0 điểm)
Một ô tô và một xe máy cùng khởi hành từ địa điểm A và đi đến địa điểm B. Xe máy đi với
vận tốc là x (km/h), ô tô đi với vận tốc lớn hơn vận tốc của xe máy là 20 km/h. Biết quãng đường
AB dài 80km. (Giả định rằng vận tốc mỗi xe là không đổi trên toàn bộ quãng đường AB .)
a) Viết phân thức đại số biểu thị thời gian đi hết quãng đường AB của ô tô và xe máy.
b) Viết biểu thức đại số biểu thị hiệu thời gian đi hết quãng đường AB của ô tô và xe máy.
c) Biết rằng thời gian xe máy đi hết quãng đường AB là 2 giờ. Hỏi ô tô đến B sớm hơn xe máy bao nhiêu phút? Bài 3 (3,0 điểm)
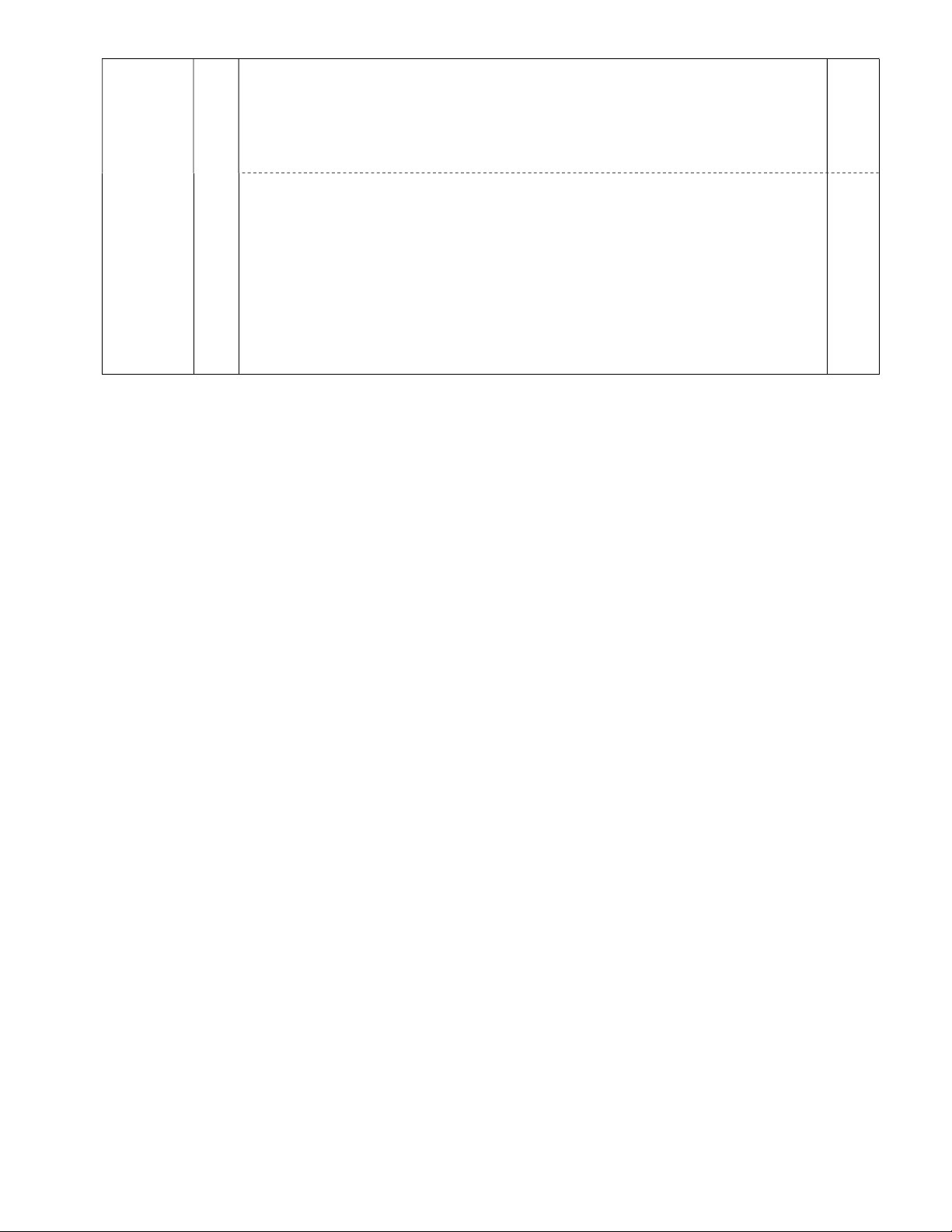
Cho tam giác ABC nhọn, có hai đường cao BE, CF cắt nhau tại điểm I. a) Chứng minh A EB đồng dạng với A FC. b) Chứng minh AFE ACB.
c) Vẽ hình bình hành BICK, đoạn thẳng AK cắt đoạn thẳng BC tại điểm N. Gọi M là FI CK
giao điểm của các đoạn thẳng AI và EF. Chứng minh và MN // IK. FA CA Bài 4 (0,5 điểm) 2 2 x z 2z
Cho các số thực dương x, , y z thỏa mãn . Chứng minh 2 yz x 2 2 2 2 x y x z y z hoặc y z.
---------------------------Hết---------------------------
HƯỚNG DẪN CHẤM KIỂM TRA GIỮA HỌC KÌ II HƯỚNG DẪN CHUNG
+) Điểm toàn bài để lẻ đến 0,25.
+) Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm.
+) Các tình huống phát sinh trong quá trình chấm do Hội đồng chấm thi quy định, thống nhất bằng biên bản.
I. Trắc nghiệm (2,5 điểm) Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A B C C A C A D A B
Mỗi câu đúng được 0,25 điểm. II. Tự luận (7,5 điểm) Bài Ý Đáp án Điểm
Tính giá trị của biểu thức B tại x 3. 0,5 a) Tính được 5 B . 0,5 3 3 Chứng minh M . 1,0 x 2 Ta có 2 x 1 x 2 x 2 M A B 2 x 2 x 2 x 4 x 0,25 Bài 1 2 x 1 x 2 x 2 x 2 x 2 x 2x 2 x 2,0 điểm b)
x x x 2 2 2 x 2 x 2 0,25 x 2x 2 x 2 2
x 2x x 2 x 2 x 2 x 2x 2 x 0,25 3x x 2 3 x 2x 2 x x 2 0,25
c) Tìm tất cả giá trị nguyên của x để biểu thức M nhận giá trị nguyên. 0,5
Lập luận được x 2 Ư 3 x 2 1 ; 3 . 0,25
Tìm được x 1; 3; 1;
5 . Đối chiếu với điều kiện xác định và kết luận 0,25 x 1 ; 3; 5 .
Viết phân thức đại số biểu thị thời gian đi hết quãng đường AB của ô tô 1,0 và xe máy. a) 80
Phân thức biểu thị thời gian đi hết quãng đường AB của xe máy là: . 0,5 x 80
Phân thức biểu thị thời gian đi hết quãng đường AB của ô tô là: . 0,5 x 20
Viết biểu thức đại số biểu thị hiệu thời gian đi hết quãng đường AB của 0,5 Bài 2 ô tô và xe máy. 2,0 điểm
b) Biểu thức đại số biểu thị hiệu thời gian đi hết quãng đường AB của ô tô 80 80 0,5 và xe máy là: . x x 20
Hỏi ô tô đến B sớm hơn xe máy bao nhiêu phút? 0,5
c) Tính được vận tốc xe máy là 40km/h. 0,25
Thay số vào biểu thức của câu b và tính được: xe ô tô đến B sớm hơn xe 0,25 máy là 40 phút. Chứng minh A EB đồng dạng với A FC. 1,25 A E F a) I Bài 3 3,0 điểm C B
Vẽ hình đúng đến câu a. 0,25 Lập luận được A EB đồng dạng với A
FC theo trường hợp g.g. 1,0 Chứng minh AFE ACB. 0,75 b) +) Lập luận được A EF đồng dạng với A
CB theo trường hợp c.g.c. 0,5 +) Suy ra AFE ACB. 0,25 FI CK Chứng minh và MN // IK. 1,0 FA CA A E M F I B N C K c) +) Lập luận được B IF ∽ C AF g.g. 0,25 BI IF CK IF +) Từ đó suy ra . 0,25 CA FA CA FA +) Lập luận được F AI ∽ C AK c g c . . FAI KAC. 0,25 AM FA +) Lập luận được F AM ∽ C AN g.g . AN CA FA AI AM AI +) Mà F AI ∽ C AK MN //IK. 0,25 CA AK AN AK Chứng minh 2 yz x hoặc y z. 0,5 Ta có: Bài 4 2 2 x z 2z 0,5 điểm 2 2 2 2 x y x z y z 0,25 4 2 2 2 2 2 2
x x z x z y z y z 2z 4 2 2 2 2 2 2
x x y x z y z 0 Suy ra: 4 2 2 2 2
x x z y z y z 2 2
x z y z 2z 4 2 2 2 2 x x z y z 2 2 2zx y 0 4 2 2 2 2
x x z y z y z 2 x z 2 2 z yz 2y 0 4 2 2 2 2
x x z y z y z 2
x z z yz 2y 0 y z 4 2 2 2 2 2 2 2
x x z y z 2x yz x z 0 y z 4 2 2 2 2 2 2 2
x x z y z 2x yz x z 0 y z 4 2 2 2 x y z 2x yz 0 0,25
y z x yz 2 2 0 Suy ra 2 yz x hoặc y z.
Nếu học sinh có cách giải khác đáp án mà đúng thì vẫn cho đủ điểm.