TRƯỜNG THCS HƯNG BÌNH
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
MÔN: TOÁN – LỚP 8 Thời gian: 90 phút
(không kể thời gian giao đề)
A. TRẮC NGHIỆM (3,0 điểm)
Câu 1. Cách viết nào sau đây không cho một phân thức A. 2 . B. x . C. x + 2 x − 4 . D. 1. x x +1 0
Câu 2 Cách viết nào dưới đây là một phân thức đại số? 5 3 − A. x . B. 12 . C. 2x −3 . D. 5 . x +1 7x − 4 0x x + 4 x +1
Câu 3. Điều kiện của x để giá trị của phân thức x −3 xác định là x + 4 A. x ≠ 3. B. x ≠ 4 − . C. x > 4 − . D. x ≠ 0 .
Câu 4 Hai phân thức A và C bằng nhau nếu B D A. . A D = . B C . B. . A D ≠ . B C . C. .
A B = C.D . D. . AC = . B D . 2
Câu 5 Giá trị của phân thức A = x −9 tại x = 5 là x − 3 A. 5 B. 7 C. 8 D. 9
Câu 6. Phân thức 2x bằng phân thức nào sau đây ? 3 − y
A. 2x . B. 2 − x . C. 2 − x . D. 3 − y . 3y 3y 3 − y 2x
Câu 7. Điều kiện của x để giá trị của phân thức x +1 xác định là x(x − 4) A. x ≠ 1 − . B. x ≠ 0 . C. x ≠ 4 .
D. x ≠ 0 và x ≠ 4
Câu 8 Giá trị của phân thức 2x −1 tại x= -1 và y = 0 là y + 3 A. 0 B. 1 − C. -1 D. 1 3
Câu 9. Trong các biểu thức dưới đây có bao nhiêu biểu thức là phân thức 2 x − 2 + 2x x 5 − 3; 3 ; ; x + 4 . 5 4 x + x 3x − 7 x −1 A. 1 B. 2 C. 3 D.4 ... 6x Câu 10. Cho 
Hãy chọn một đa thức thích hợp điền vào chỗ trống 2y 4 A. 3x B. 3 C. 3xy D. 3y A x +
Câu 11 Với x ≠ 5 đa thức A thỏa mãn 2 = là: x − 5 x − 5
A. A = x + 2. B. 2
A = x + 4 .x C. 2
A = x +16 .x D. 2 A = x + 4. 3x +1
Câu 12. Mẫu thức của phân thức 2x − 3 là. A. 3x+ 1 B. 3x C. 2x - 3 D. 2x
B. TỰ LUẬN (7,0 điểm)
Câu 13. (1 điểm) Rút gọn các biểu thức sau: 6x A − = (y ≠ 0) b) B =  2
1  1 với x ≠ 0 và x ≠ 1 8 − y   :  x x +1 x
Câu 14. (1,5 điểm) Giải các phương trình sau a) 0,5x + 3 = 0 b) 5 1 − x = 0 6 6
Câu 15. (1,0 điểm) Một tổ sản xuất dự định mỗi ngày làm 120 sản phẩm, trong một thời gian
nhất định. Khi thực hiện, mỗi ngày tổ sản xuất được 150 sản phẩm. Vì vậy, tổ đã hoàn thành
công việc sớm hơn 4 ngày so với kế hoạch. Hỏi ban đầu tổ dự định làm tất cả bao nhiêu sản phẩm?
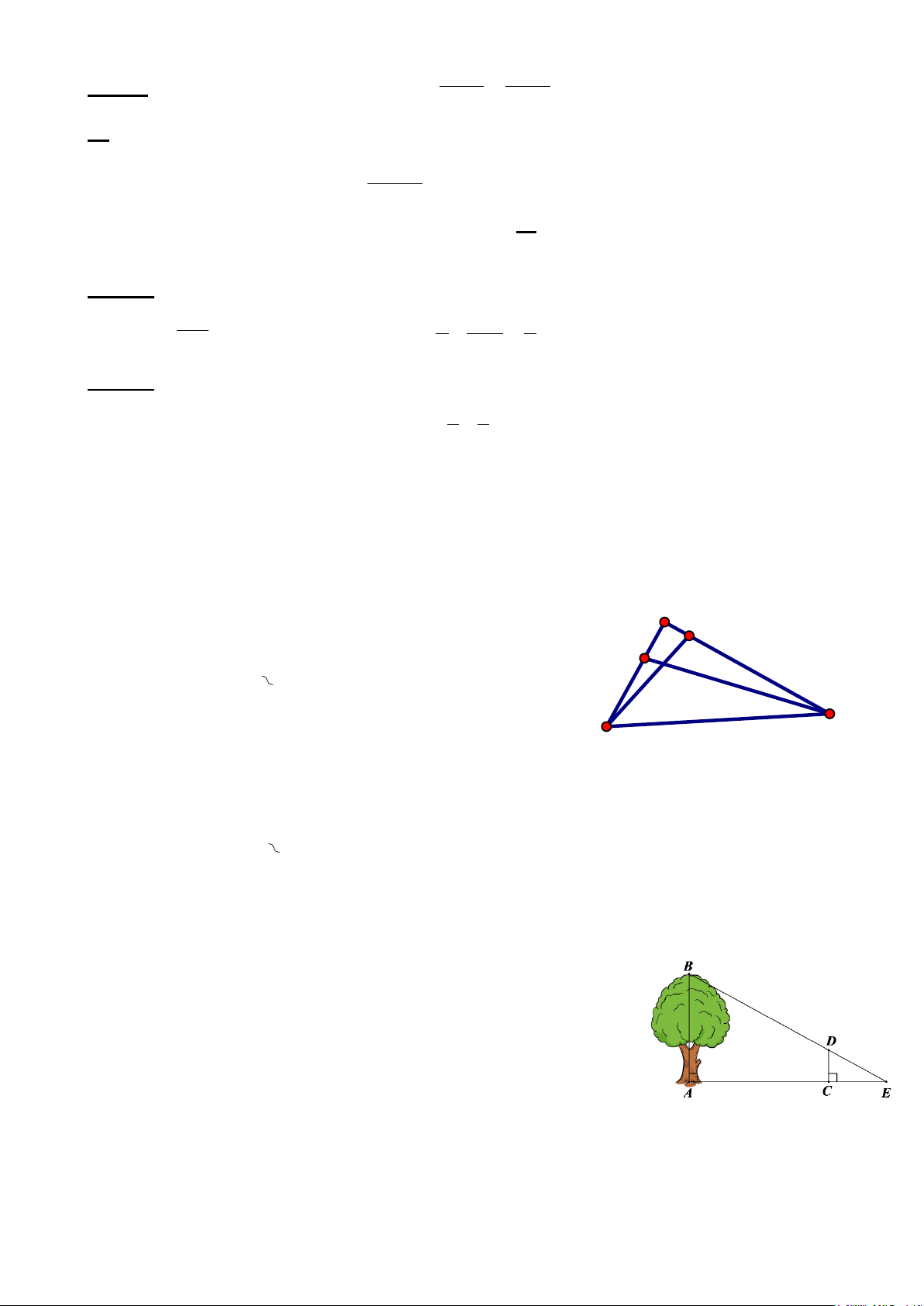
Câu 16. (1 điểm) Cho hình vẽ biết FG = 6cm; FH = 8cm; F GH=10cm; FI = 1,5cm; FK = 2cm I
a) Chứng minh ∆FGH là tam giác vuông K
b) Chứng minh ∆FIG ∆ FKH H G
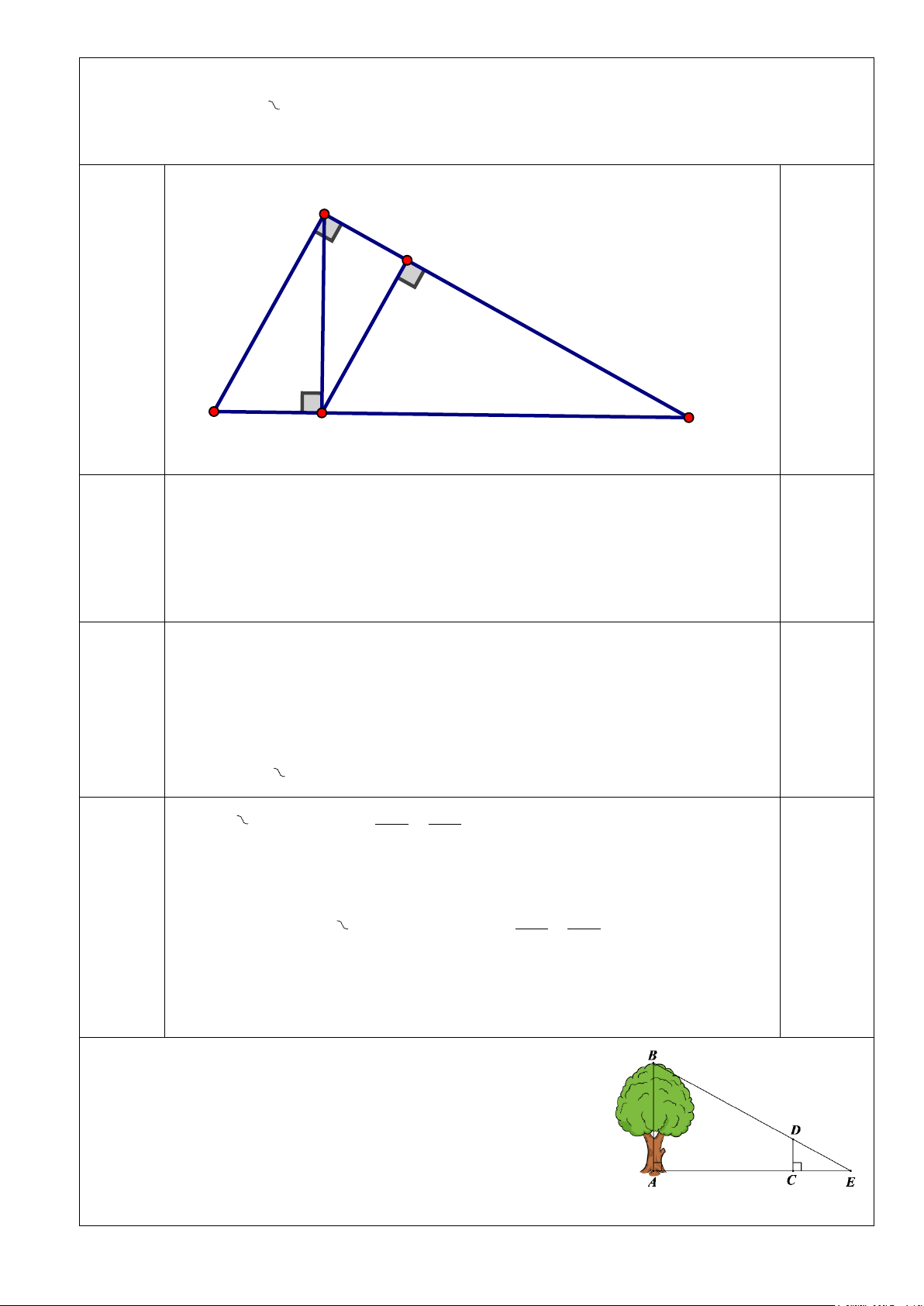
Câu 17. (2 điểm) Cho tam giác ABC vuông tại A, đường cao AH (H∈BC). Kẻ HD ⊥AC (D∈AC)
a) Cho AB = 3cm; BC = 5cm. Tính AC b)Chứng minh ∆ADH ∆AHC
c) Chứng minh AD.AC = BH.CH
Câu 18: (0,5 điểm) Để đo chiều cao của một cái cây
(AB), người ta dùng một cái cọc (CD) cắm xuống mặt
đất. Sau đó di chuyển cọc sao cho cọc song song với
cây, đồng thời đỉnh cây (B), đỉnh cọc (D) cùng với vị trí
quan sát (E) là 3 điểm thẳng hàng (xem hình vẽ). Biết
cọc cao 1,5 m, chân cọc (C) và gốc cây (A) lần lượt cách
vị trí quan sát (E) là 2,3 m và 10 m. Tính chiều cao của
cây. (Kết quả làm tròn đến chữ số thập phân thứ nhất).
---------Hết ---------
Đáp án và biểu điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 801 C D B A B A D B A C C D 802 C B A B A C D A D B D C 803 D A C B D B D C B A C A 804 C B A A B D A D C B C D Câu Đáp án Điểm
Câu 13. (1 điểm) Rút gọn các biểu thức sau: 6x A − = (y ≠ 0) b) B =  2
1  1 với x ≠ 0 và x ≠ 1 8 − y   :  x x +1 x 6x − 6x − : 2 3 − x A = = = (y ≠ 0) 0.5 8y 8y : 2 4y 2(x +1) ) − x b = .x 0.25 x(x +1) x + 2 x + 2 = .x = 0.25 x(x +1) x +1
Câu 14. (1,5 điểm) Giải các phương trình sau a) 0,5x + 3 = 0 b) 5 1 − x = 0 6 6 a) 0,5x = -3 0.25 x= -3:0,5 0.25 x = -6 0.25
Vậy phương trình có nghiệm là x = -6 b) 1 5 x = 0.25 6 6 5 1 x = : 0.25 6 6 x=5 0.25
Vậy phương trình có nghiệm là x = 5
Câu 15. (1,0 điểm) Một tổ sản xuất dự định mỗi ngày làm 120 sản phẩm. Khi thực hiện, mỗi
ngày tổ sản xuất được 150 sản phẩm, vì vậy tổ đã hoàn thành công việc sớm hơn 4 ngày so với
kế hoạch. Hỏi ban đầu tổ dự định làm tất cả bao nhiêu sản phẩm?
Gọi số sản phẩm ban đầu tổ dự định làm là x (x ∈ N*) 0.25 x 0.25
Thời gian tổ dự định hoàn thành công việc là 120 (ngày) x
Thời gian thực tế tổ hoàn thành công việc là 150 (ngày)
Vì tổ hoàn thành công việc sớm hơn 4 ngày so với kế hoạch nên ta có 0.25 phương trình x x − = 4 120 150 5x 4x 2400 0.25 − = 600 600 600 x= 2400 (thỏa mãn)
Vậy ban đầu tổ dự định làm 2400 sản phẩm
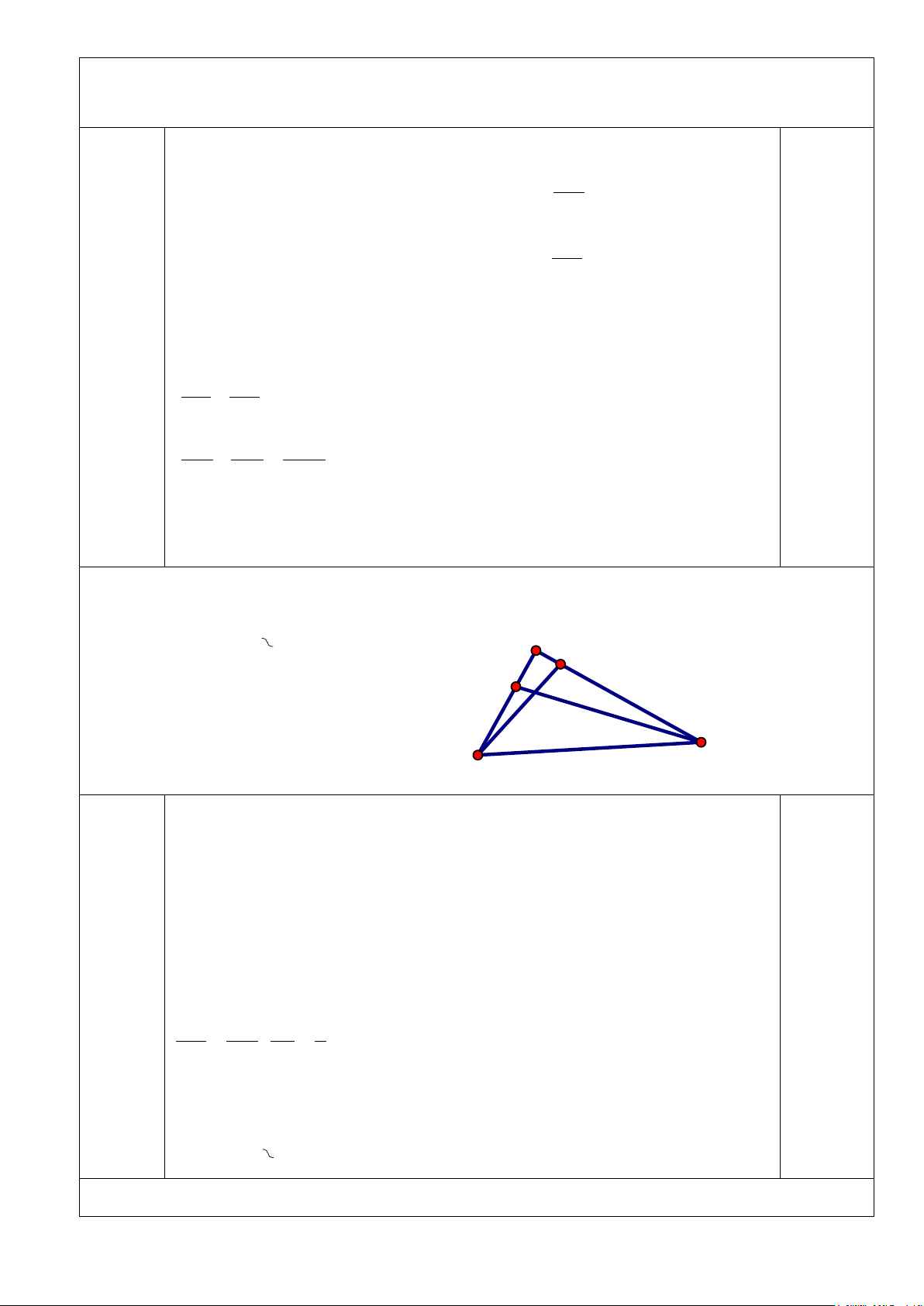
Câu 16. (1 điểm) Cho hình vẽ biết FG = 6cm; FH = 8cm; GH=10cm; FI = 1,5cm; FK = 2cm
a) Chứng minh ∆FGH là tam giác vuông F
b) Chứng minh ∆FIG ∆ FKH I K H G a Xét tam giác FGH có 0.25 GH2 = 102 = 100 FG2 + FH2 = 62 + 82 = 100 Suy ra GH2 = FG2 + FH2 0.25
Vậy tam giác FGH là tam giác vuông tại F b Xét ∆FIG và ∆ FKH có FI FG 1,5 6  = = FK FH  2 8    0.25  GFH Chung Vậy ∆FIG ∆ FKH (c.g.c) 0.25
Câu 17. (2 điểm) Cho tam giác ABC vuông tại A, đường cao AH (H∈BC). Kẻ HD ⊥AC (D∈AC)
a) Cho AB = 3cm; BC = 5cm. Tính Aca) b)Chứng minh ∆ADH ∆AHC
c) Chứng minh AD.AC = BH.CH 0.5 A D B H C a
∆ABC vuông tại A, áp dụng định lý Pythagore ta có 0.25 AC2 = BC2 - AB2 AC2 = 52 - 32 AC = 4cm 0.25 b Xét ∆ADH và ∆AHC có 0.25  =  0 D A H AHC = 90  HAC Chung Vậy ∆ADH ∆AHC (g.g) 0.25 c ∆ADH ∆AHC suy ra D A AH = AH AC Hay AH2 = AC.AD (1) 0.25
Chứng minh ∆BHA ∆AHC (g.g) suy ra H A BH 0.25 = CH AH Hay AH2 = BH.CH (2)
Từ (1) và (2) suy ra AD.AC = BH.CH
Câu 18: (0,5 điểm) Để đo chiều cao của một cái cây
(AB), người ta dùng một cái cọc (CD) cắm xuống mặt
đất. Sau đó di chuyển cọc sao cho cọc song song với
cây, đồng thời đỉnh cây (B), đỉnh cọc (D) cùng với vị
trí quan sát (E) là 3 điểm thẳng hàng (xem hình vẽ).
Biết cọc cao 1,5 m, chân cọc (C) và gốc cây (A) lần lượt cách vị trí quan sát (E) là 2,3 m
và 10 m. Tính chiều cao của cây. (Kết quả làm tròn đến chữ số thập phân thứ nhất). Xét ECD và ∆EAB có 0.25  =  0 ECD A E B = 90 Góc E chung Vậy ∆ECD ∆EAB (g.g) Suy ra EC CD = A E AB 2,3 1,5 0.25 = 10 AB 1,5.10 AB = ≈ 6,5(m) 2,3
Vậy chiều cao của cây là 6,5m
Xem thêm: ĐỀ THI GIỮA HK2 TOÁN 8
https://thcs.toanmath.com/de-thi-giua-hk2-toan-8
Document Outline

• Nghệ An - Đáp án kiểm tra giữa kỳ II 24-25 Hưng Bình
• GK2 - 8