












Preview text:
1. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 MÔN TOÁN – LỚP 10
Mức độ đánh giá Tổng % điểm (4-11) (12) TT Chương/Chủ đề
Nội dung/đơn vị kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao (1) (2) (3) TNKQ TL TNKQ TL TNKQ TL TNKQ TL
Mệnh đề toán học. Mệnh đề
phủ định. Mệnh đề đảo. Mệnh
đề tương đương. Điều kiện 1-3 0 4-6 0 0 0 0 0 12% 1 Tập hợp. Mệnh đề (8 tiết)
cần và đủ. (3,5 tiết)
Tập hợp. Các phép toán trên
tập hợp (4,5 tiết) 7-9 0 10-11 TL1a 12 TL1b 0 0 17%
Bất phương trình Bất phương trình bậc nhất 17 0 0 11% 2
và hệ bất phương hai ẩn và ứng dụng 3 tiết) 13-14 0 15-16
trình bậc nhất hai TL2a TL2b ẩn
Hệ bất phương trình bậc nhất (7 tiết)
hai ẩn và ứng dụng (4 tiết) 18 0 19-20 21 0 0 15%
Giá trị lượng giác của một
góc từ 0° đến 180°.(2,5 tiết) 22-24 0 25-28 0 0 0 0 0 26%
Hệ thức lượng Hệ thức lượng trong tam
3 trong tam giác. giác. Định lí côsin. Định lí Vectơ (7 tiết)
sin. Công thức tính diện tích 29-31 0 32-33 0 34, 35 TL3a 0 TL3b 19%
tam giác. Giải tam giác (4,5 tiết) Tổng 15 0 15 2 5 2 0 2 Tỉ lệ % 30% 40% 20% 10% 100% Tỉ lệ chung 70% 30% 100%
2. BẢN ĐẶC TẢ ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 MÔN TOÁN - LỚP 10
Số câu hỏi theo mức độ nhận thức
STT Chương/chủ đề Nội dung
Mức độ kiểm tra, đánh giá Nhận biêt Thông hiểu Vận dụng Vận dụng cao 1 Tập hợp.
Mệnh đề toán học. Nhận biết : Mệnh đề
Mệnh đề phủ định. – Phát biểu được các mệnh đề toán học, bao Mệnh đề đảo.
gồm: mệnh đề phủ định; mệnh đề đảo; mệnh Mệnh đề tương
đề tương đương; mệnh đề có chứa kí hiệu ∀,
đương. Điều kiện ∃; điều kiện cần, điều kiện đủ, điều kiện cần cần và đủ. và đủ. 3 (TN) 3 (TN) Thông hiểu: Câu 1, Câu 4,
– Thiết lập được các mệnh đề toán học, bao
gồm: mệnh đề phủ định; mệnh đề đảo; mệnh Câu 2, Câu 5,
đề tương đương; mệnh đề có chứa kí hiệu ∀, Câu 3 Câu 6
∃; điều kiện cần, điều kiện đủ, điều kiện cần và đủ.
– Xác định được tính đúng/sai của một mệnh
đề toán học trong những trường hợp đơn giản. Tập hợp. Các Nhận biết :
phép toán trên tập – Nhận biết được các khái niệm cơ bản về tập hợp
hợp (tập con, hai tập hợp bằng nhau, tập
rỗng) và biết sử dụng các kí hiệu ⊂, ⊃, ∅. 2 (TN) Thông hiểu: 3 (TN) + 1 (TN) Câu 10,
– Thực hiện được phép toán trên các tập hợp Câu 7, Câu 12 Câu 11
(hợp, giao, hiệu của hai tập hợp, phần bù của Câu 8, + 1 (TL)
một tập con) và biết dùng biểu đồ Ven để +1(TL) Câu 9 Câu 1b
biểu diễn chúng trong những trường hợp cụ Câu 1a thể. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với phép toán trên tập hợp (ví dụ: những bài
toán liên quan đến đếm số phần tử của hợp các tập hợp,...). 2 Bất phương
Bất phương trình, Nhận biết :
trình và hệ bất hệ bất phương
– Nhận biết được bất phương trình và hệ bất phương trình
trình bậc nhất hai phương trình bậc nhất hai ẩn.
bậc nhất hai ẩn ẩn và ứng dụng Thông hiểu:
– Biểu diễn được miền nghiệm của bất
phương trình và hệ bất phương trình bậc nhất
hai ẩn trên mặt phẳng toạ độ. + 4 (TN) Vận dụng: 3 (TN) Câu 15, 2 (TN)
– Vận dụng được kiến thức về bất phương Câu 13, Câu 16,
trình, hệ bất phương trình bậc nhất hai ẩn vào Câu 17, 1 (TL) Câu 14, Câu 19,
giải quyết một số bài toán thực tiễn (đơn Câu 21 Bài 2b Câu 18 Câu 20
giản, quen thuộc) (ví dụ: bài toán tìm cực trị + 1 (TL)
của biểu thức F = ax + by trên một miền đa Bài 2a giác,...). Vận dụng cao:
– Vận dụng được kiến thức về bất phương
trình, hệ bất phương trình bậc nhất hai ẩn vào
giải quyết một số bài toán thực tiễn (phức
hợp, không quen thuộc). 3
Hệ thức lượng Giá trị lượng giác Nhận biết : 6 (TN) trong tam giác. 6 (TN)
của một góc từ 0° – Nhận biết được giá trị lượng giác của một góc Câu 22, Câu 25, + 1 (TN)
đến 180°. Định lí từ 0° đến 180°. Câu 23, Câu 26, Câu 34,
côsin. Định lí sin. Thông hiểu: Câu 24, 1 (TL) Câu 27, Câu 35 Công thức tính
– Tính được giá trị lượng giác (đúng hoặc gần Câu 29, Bài 3b
diện tích tam giác. đúng) của một góc từ 0° đến 180° bằng máy tính Câu 28, + 1 (TL) Câu 30, Giải tam giác cầm tay. Câu 32, Bài 3a Câu 31
– Giải thích được hệ thức liên hệ giữa giá trị Câu 33
lượng giác của các góc phụ nhau, bù nhau.
– Giải thích được các hệ thức lượng cơ bản trong
tam giác: định lí côsin, định lí sin, công thức tính diện tích tam giác. Vận dụng:
– Mô tả được cách giải tam giác và vận dụng
được vào việc giải một số bài toán có nội dung
thực tiễn (đơn giản, quen thuộc) (ví dụ: xác định
khoảng cách giữa hai địa điểm khi gặp vật cản,
xác định chiều cao của vật khi không thể đo trực tiếp,...). Vận dụng cao:
- Vận dụng được cách giải tam giác vào việc giải
một số bài toán có nội dung thực tiễn (phức hợp,
không quen thuộc). Tổng 15TN 15TN+2TL 5TN+2TL 2TL Tỉ lệ % 30% 40% 20% 10% Tỉ lệ chung 70% 30% SỞ GD VÀ ĐT NINH BÌNH
KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT DÂN TỘC NỘI TRÚ NĂM HỌC 2023- 2024 Môn: TOÁN - Lớp 10
Thời gian: 90 phút( Không kể thời gian phát đề) ĐỀ SỐ 101
1. Trắc nghiệm (7 điểm)
Câu 1. Câu nào là một mệnh đề?
A. 13 là số nguyên tố. B. Bây giờ là mấy giờ?
C. Cảnh báo đường trơn, lái xe cẩn thận! D. Các em phải học hành chăm chỉ nhé!
Câu 2. Cho mệnh đề chứa biến P(n) 2
:"n +1 chia hết cho 10 ". Giá tri nào của n trong các giá trị sau
làm cho P(n) là mệnh đề đúng? A. n =1. B. n = 2 . C. n = 3. D. n =15.
Câu 3. Cho mệnh đề: “Nếu tam giác có hai góc bằng 60o thì tam giác đó là tam giác đều”.
Mệnh đề đảo của mệnh đề trên là:
A. Nếu tam giác có hai góc bằng 60o thì tam giác đó không là tam giác đều.
B. Nếu tam giác là tam giác đều thì tam giác đó có hai góc bằng 60o .
C. Tam giác là tam giác đều nếu và chỉ nếu tam giác đó có hai góc bằng 60o .
D. Nếu một tam giác là tam giác đều thì tam giác đó có hai góc bằng nhau.
Câu 4. Phủ định của mệnh đề P(x) 2 :" x
∃ ∈ , 5x − 3x =1" là A. 2 " x
∃ ∈ , 5x − 3x =1". B. 2 " x
∀ ∈ , 5x − 3x =1". C. 2 " x
∀ ∈ , 5x − 3x ≠ 1". D. 2 " x
∃ ∈ , 5x − 3x ≥1".
Câu 5. Cho A = {0;2;4; }
6 . Tập A có bao nhiêu tập con có 2 phần tử? A. 6 . B. 4 . C. 8 . D. 7 . Câu 6.
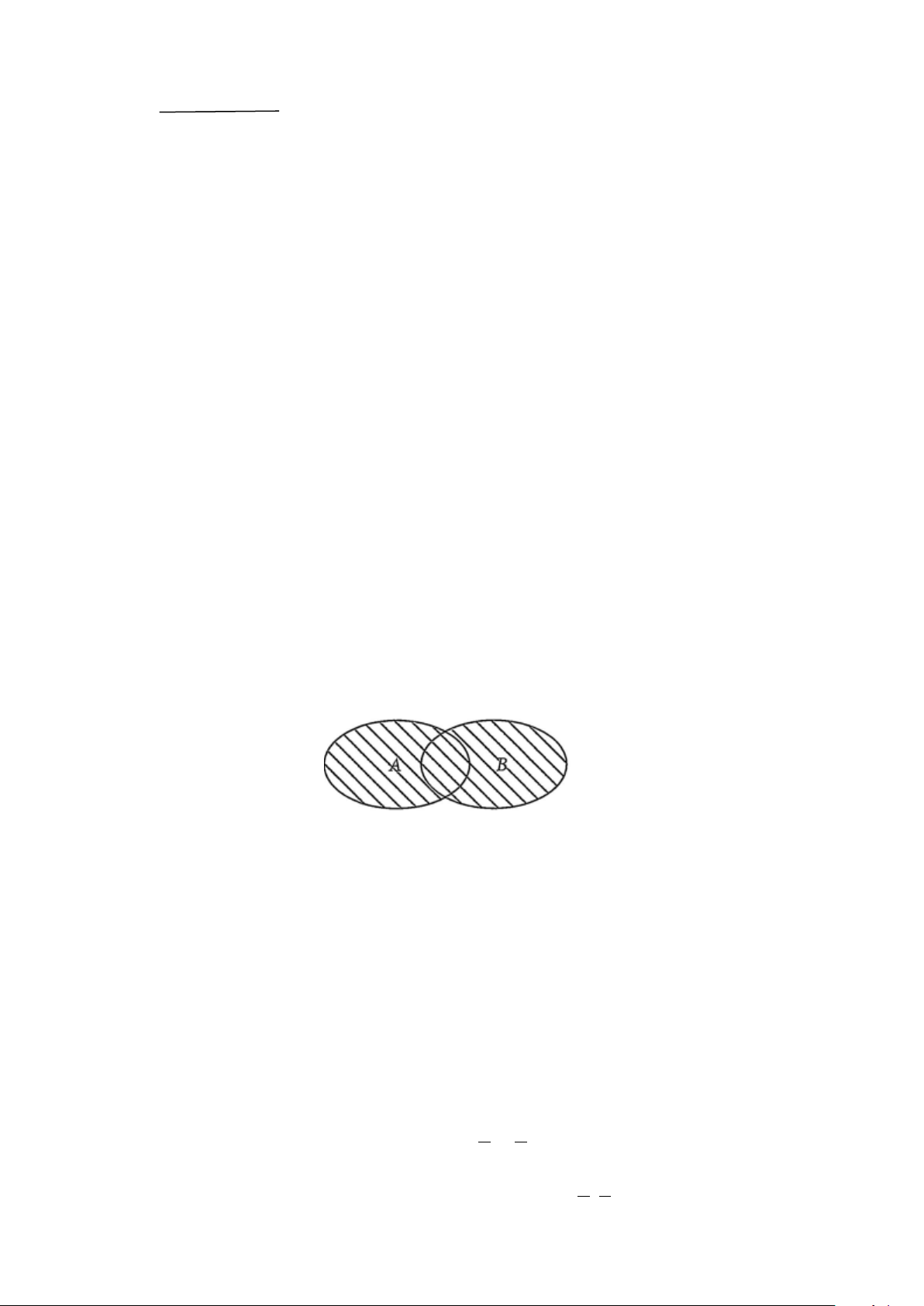
Cho biểu đồ Ven sau đây. Phần được gạch sọc biểu diễn tập hợp nào?
A. A \ B .
B. B \ A .
C. A∪ B .
D. A∩ B
Câu 7. Cho tập hợp X = {x∈, x < }
5 . Tập X được viết dưới dạng liệt kê là A. X = {1;2;3 } ;4 .
B. X = {0;1;2;3; } 4 .
C. X = {0;1;2;3;4; } 5 .
D. X = {1;2;3;4; } 5 .
Câu 8. Cho hai tập hợp A = { 2; − 1
− ;0;1;2;3;4;5}; B = { 4; − 3 − ; 2; − 1
− ;0;1}. Hợp của hai tập hợp A và B là:
A. A∪ B = { 4 − ; 3}
− B. A∪ B = { 2; − 1 − ;0;1;2;3;4;5}
C. A∪ B = { 2; − 1
− ;0;1} D. A∪ B = { 4; − 3 − ; 2; − 1 − ;0;1;2;3;4;5}
Câu 9. Cho tập E = ( 1;
− 5], tập F = [2;7) . Tìm tập hợp E ∩ F ? A. (2;5]. B. ( 1; − 2]. C. [2;5]. D. (2;5) .
Câu 10. Cho tập hợp 1
A = {1; ;2} và B = {2;3;4}. Khẳng định nào sau đây là đúng? 2
A. A∪ B = {2}. B. 1
A∪ B = {1; 2;3;4}. C. 1
A \ B = {1; ;3}. D. A∩ B = {1;2;3} 2 2
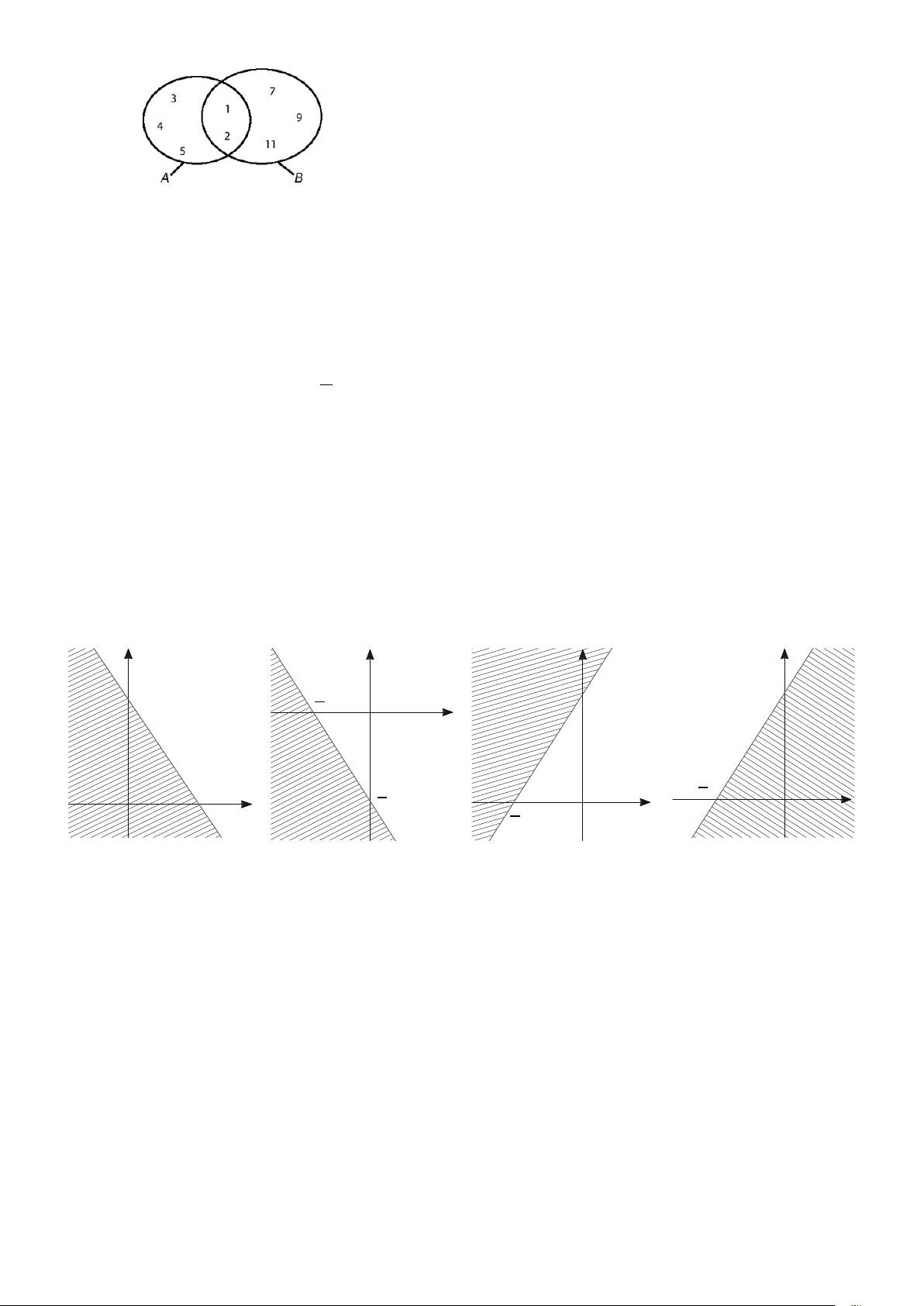
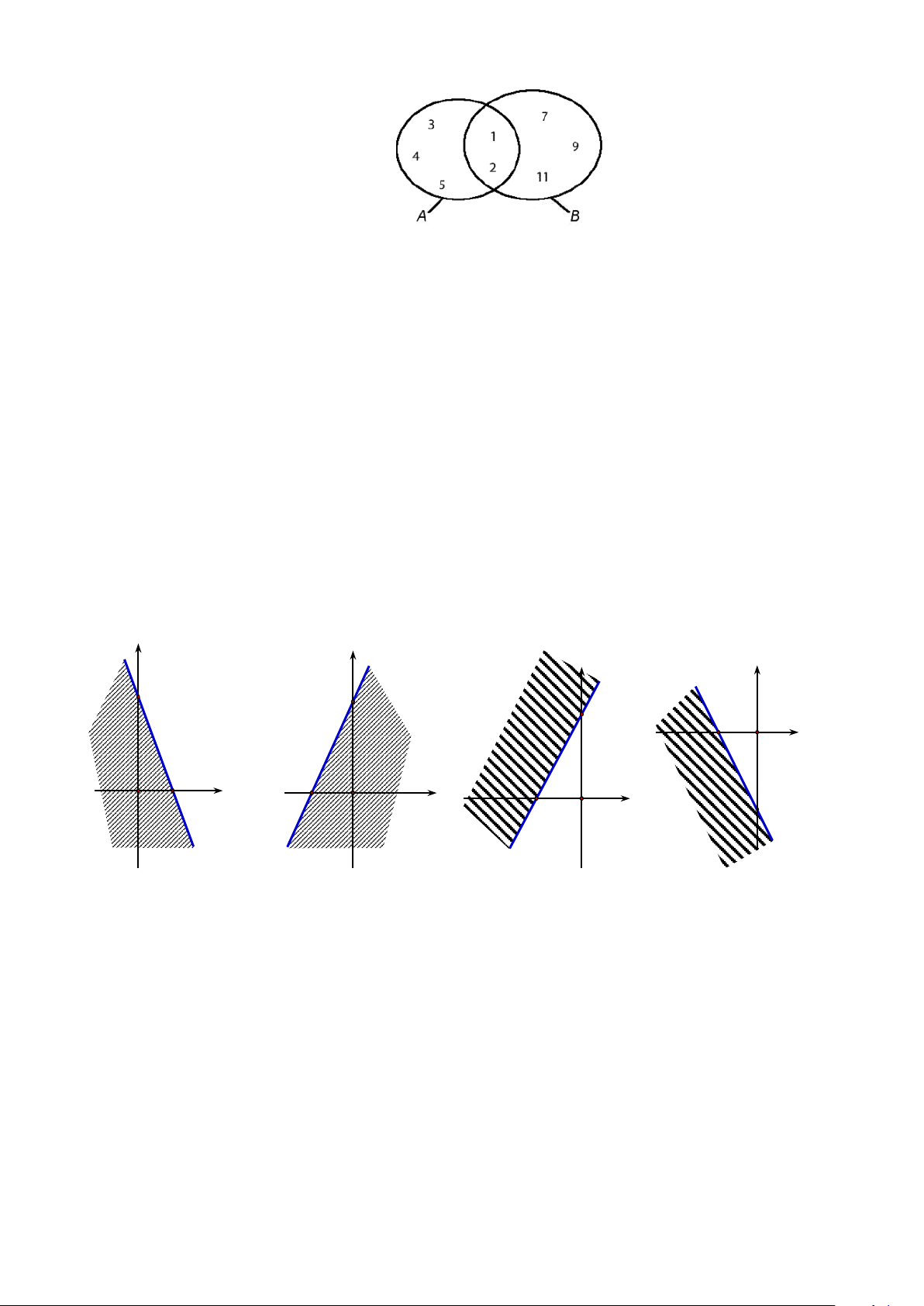
Câu 11. Cho hai tập hợp A và B được mô tả bởi biểu đồ VEN sau đây
Khẳng định nào sau đây là sai ?
A. B \ A = {7;9;1 } 1 .
B. A∩ B = {1; } 2 .
C. A∪ B = {3;4;5;7;9;1 } 1 .
D. A \ B = {3;4; } 5 .
Câu 12. Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn
Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh? A. 54 B. 40 C. 26 D. 68
Câu 13. Bất phương trình nào sau đây là bất phương phương trình bậc nhất hai ẩn? 1 A. 2 2
x + y ≤ 2007 . B. 2
x + 3y + 5 < 0. C. 2
2x + 3y ≥ 5 . D. + < . 2 2x 3y 5
Câu 14. Cho bất phương trình 2x + y > 3. Khẳng định nào sau đây là đúng?
A. Bất phương trình đã cho có nghiệm duy nhất.
B. Bất phương trình đã cho vô nghiệm.
C. Bất phương trình đã cho có vô số nghiệm.
D. Bất phương trình đã cho có tập nghiệm là (3;+∞) .
Câu 15. Cặp số nào là một nghiệm của bất phương trình 2x + 3y ≤ 5 ? A. (1;2) B. ( 2 − ;1) C. (5;3) D. ( 1; − 4)
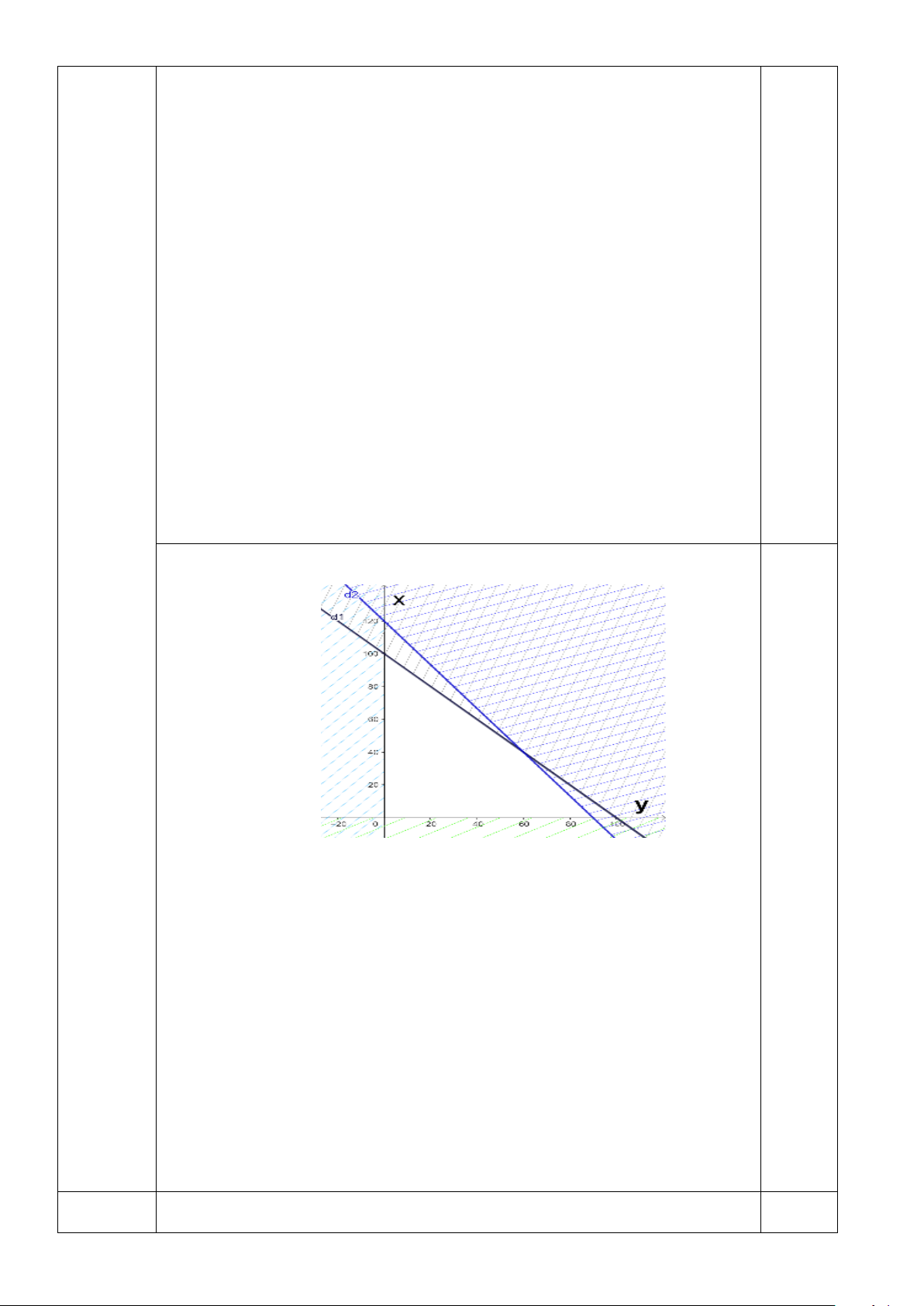
Câu 16. Miền nghiệm của bất phương trình 3x − 2y > 6
− được biểu diễn bởi phần không gạch chéo
trong hình nào được cho dưới đây ? y d y y d y 3 3 2 O 3 x d d 2 2 3 O x 2 x O x O Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 17. Bà Mai đi chợ bà muốn mua x kg gạo và y kg thịt lợn sao cho số tiền để mua không vượt quá
700.000 đồng. Biết giá một kg gạo là 3.000 đồng, một kg thịt là 200.000 đồng. Bất phương trình bậc nhất
hai ẩn x và y thoả mãn điều kiện trên là
A. 3x + 200y ≥ 700 . B. 3x + 200y ≤ 700 . C. x + y ≤ 700.000 . D. 3x + 200y = 700 .
Câu 18. Hệ bất phương trình nào sau đây không là hệ bất phương trình bậc nhất hai ẩn? 2 − x ≤ 0 3 y ≥ 0
4x − y ≥ 0 x + y ≥ 0 A. . B. . C. . D. . 5
x − 2y < 0 x − y ≥ 0
−x − 3y < 0 2
2x − 2y ≥ 0
x − y > 2 −
Câu 19. Cho hệ bất phương trình x −3y + 4 < 0. Mệnh đề nào sau đây là đúng? x + y ≥ 0 A. Điểm (
A 1;1) thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm O(0;0) thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm B(4;3) thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm C(3;2) thuộc miền nghiệm của hệ bất phương trình đã cho
Câu 20. Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? y > 0 y > 0 x > 0 x > 0 A. . B. . C. . D. . x + 2y < 2 2x + y < 2 2x + y < 2 x + 2y > 2
Câu 21. Biểu thức F( ;
x y) = y − x đạt giá trị nhỏ nhất tại điểm M có toạ độ ( ;
x y) thuộc miền nghiệm
2x − y ≥ 2
x − 2y ≤ 2
của hệ bất phương trình
. Tọa độ điểm M là: x + y ≤ 5 x ≥ 0 A. (4;1) B. 8 7 ; − C. 2 2 ;− D. (5;0) 3 3 3 3
Câu 22. Cho góc tù. Điều khẳng định nào sau đây là đúng? A. cosα > 0 B. cot α > 0.
C. sin α > 0. D. tan α > 0 .
Câu 23. Trong các đẳng thức sau đây đẳng thức nào là đúng? ° 3 ° 1 ° 3 A. os c 30 = B. os c 30 = C. ° 1 os c 30 = − . D. os c 30 = − 2 2 2 2
Câu 24. Trong các mệnh đề sau, mệnh đề sai là A. 0
cot(180 −α) = −cotα . B. 0
cos(180 −α) = cosα . C. 0
tan(180 −α) = − tanα . D. 0 sin(180 −α) = sinα .
Câu 25. Giá trị của cos30° sin 60° + bằng bao nhiêu? A. 3 . B. 3 . C. 3 . D. 1. 3 2
Câu 26. Giá trị của biểu thức ( 2 sin135°
3 sin120° cos90° )(3tan135° 2cot 45° + − + ) là: A. 2, − 5 B. 2,5 C. 2 D. 2 −
Câu 27. Cho hình bình hành ABCD như hình vẽ bên dưới. Biết rằng 3
cosα = . Khi đó cos β bằng 5 D C α β A B A. 2 . B. 3 − . C. 4 . D. 3 . 5 5 5 5 Câu 28. α + α Cho 1
tanα = . Giá trị của biểu thức 3sin 4cos A = là: 3 2sinα − 5cosα A. 15 − . B. 13 − . C. 15 . D. 13. 13 13
Câu 29. Cho tam giác ABC , mệnh đề nào sau đây đúng? A. 2 2 2
a = b + c + 2bccos A . B. 2 2 2
a = b + c − 2bccos A. C. 2 2 2
a = b + c − 2bccosC . D. 2 2 2
a = b + c − 2bccos B .
Câu 30. Cho tam giác ABC với các kí hiệu thông thường. Kết luận nào sau đây sai?
A. S = p( p − a)( p −b)( p − c) ⋅ B. 1
S = absin C ⋅ 2 C. abc
S = pr ⋅ D. S = ⋅ 4r
Câu 31. Cho tam giác ABC có góc ˆA 30° =
.Diện tích tam giác ABC là: A. 1 ab B. 1 bc C. 1 − ab D. 1 bc 4 2 2 4
Câu 32. Cho tam giác ABC có ˆ b 8c , m c 9c , m A 60° = = =
. Độ dài cạnh a là:
A. 73cm .
B. 217cm . C. 8cm . D. 113cm . Câu 33.
Cho tam giác ABC có độ dài cạnh AC = 24 góc ˆB 150° =
.Bán kính đường tròn ngoại
tiếp tam giác ABC là: A. 12. B. 8 3 . C. 24. D. 48.
Câu 34. Một mảnh đất hình tam giác có độ dài các cạnh là 10 , m 30 , m 36
m . Diện tích mảnh đất (làm tròn
kết quả đến hàng phần mười) là: A. 2 150 m . B. 2 180 m . C. 2 130,5 m . D. 2 135 m .
Câu 35. Ở giữa một cái hồ có một cái đảo nhỏ. Để tính khoảng cách từ điểm A trên đảo đến điểm B
trên bờ hồ, người ta chọn điểm C . Sau đó thực hiện đo các góc B , C và khoảng cách BC . Biết rằng
B 88 , C 85 và BC 50 m , tính khoảng cách từ A đến B (làm tròn kết quả đến hàng phần mười). C A 85° 50 88° B A. 415,4 m. B. 412,7 m. C. 410 m.
D. 408,7 2. Tự
luận (3,0 điểm)
Câu 1. (1,0 điểm)
a) Cho các tập hợp A ={1;2;3; } 7 và B = {2;4;6;7; }
8 . Tìm các tập hợp A∪ B, A \ . B .
b) Cho các tập hợp khác rỗng m + 3 A m 1; = − và B = ( ; −∞ 3
− ) ∪[3;+∞) . Gọi S 2 là tập hợp các giá
nguyên dương của m để A∩ B ≠ ∅ . Tìm số tập hợp con của S
Câu 2. (1,0 điểm)
a) Biểu diễn miền nghiệm của bất phương trình trình 3x + 2y ≥ 6 −
b) Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun mẫu mới trong dịp tết này với số
vốn đầu tư không quá 72 triệu đồng. Loại dài tay giá mua vào 800.000 đồng và lãi 150.000 đồng 1 áo,
loại ngắn tay giá mua vào 600.000 đồng và lãi 120.000 đồng 1 áo. Cửa hàng ước tính nhu cầu của khách
không quá 100 cái cho cả 2 loại. Lập phương án kinh doanh sao cho có lãi nhất.
Câu 3. (1,0 điểm)
a) Bạn Nam thả hai con diều cùng một lúc. Con diều thứ nhất Nam thả hết 216 m dây, con diều thứ hai
hết 218 m dây. Nam ước tính góc giữa hai đường dây diều là 30° (hình bên). Tính khoảng cách giữa hai con diều.
b) Trên biển, tàu B ở vị trí cách tàu A 53 km về hướng 0
N34 E . Sau đó, tàu B chuyển động thẳng đều
với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn
50km/h để đuổi kịp tàu B. Hỏi tàu A cần phải chuyển động theo hướng nào và sau bao lâu tàu A đuổi kịp tàu B?
--------------Hết--------------- SỞ GD VÀ ĐT NINH BÌNH
KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT DÂN TỘC NỘI TRÚ NĂM HỌC 2023- 2024
Môn: TOÁN - Lớp 10 ĐỀ SỐ 102
Thời gian: 90 phút (Không kể thời gian phát đề) 1. Trắc nghiệm
Câu 1. Trong các câu sau, câu nào không phải là một mệnh đề
A. Ăn phở rất ngon! B. 2
∃x∈, x +1> 0
C. Số 18 chia hết cho 6. D. 2 + 8 = 6.
Câu 2. Cho mệnh đề chứa biến P(x) 2
: ' x > 3x ' với x là số thực. Mệnh đề nào đúng? A. P(3) B. P(4) C. P(1) D. P(2)
Câu 3. Cho mệnh đề: “Nếu tam giác có hai góc bằng 60o thì tam giác đó là tam giác đều”.
Mệnh đề đảo của mệnh đề trên là:
A. Nếu tam giác có hai góc bằng 60o thì tam giác đó không là tam giác đều.
B. Nếu một tam giác là tam giác đều thì tam giác đó có hai góc bằng nhau.
C. Tam giác là tam giác đều nếu và chỉ nếu tam giác đó có hai góc bằng 60o .
D. Nếu tam giác là tam giác đều thì tam giác đó có hai góc bằng 60o .
Câu 4. Phủ định của mệnh đề 2
P(x) = ' x
∀ ∈ , x +1> 0' là: A. 2 ' x
∃ ∈ , x +1> 0' B. 2 '' x
∀ ∉ , x +1> 0'' C. 2 ' x
∀ ∉ , x +1≤ 0' D. 2 ' x
∃ ∈ , x +1≤ 0'
Câu 5. Cho A = { ;
a b;c;d} . Tập A có bao nhiêu tập con có 2 phần tử? A. 6 . B. 4 . C. 8 . D. 7 .
Câu 6. Cho biểu đồ Ven sau đây. Phần được gạch sọc biểu diễn tập hợp nào?
A. A \ B .
B. B \ A .
C. A∪ B .
D. A∩ B
Câu 7. Cho tập hợp X = {x∈, x ≤ }
4 . Tập X được viết dưới dạng liệt kê là A. X = {1;2;3 } ;4 .
B. X = {0;1;2;3; } 4 .
C. X = {0;1;2;3;4; } 5 .
D. X = {1;2;3;4; } 5 .
Câu 8. Cho hai tập hợp: A = {0;1;2;3;4;5;6;7;8; } 9 ; B = { 4; − 3 − ; 2; − 1 − ;0;1;2; } 3 .
Giao của hai tập hợp A và B là:
A. A∩ B = { 4; − 3 − ; 2; − 1
− ;0;1;2;3;4;5;6;7;8;9} B. A∩ B = {0;1;2;3;4}
C. A∩ B = {0;1;2;3} D. A∩ B = { 4 − ; 3 − ; 2 − ; 1 − }
Câu 9. Cho các tập số A = [ 2;
− 5]; B = (0;+∞). Khi đó A∩ B bằng?
A. A∩ B = [0;5]. B. A∩B = (0;5]. C. A∩B = ( 2;
− +∞]. D. A∩ B = (0;5).
Câu 10. Cho hai tập hợp A = {0;1;2; } 3 và 1 1 B 1; ;0; ;1;3 = − −
. Mệnh đề nào sau đây đúng? 2 2
A. A \ B = { 3 − ; } 2 .
B. A \ B = { } 2 . C. 1 1 A B ; ∪ = −
.D. A∩ B = { 1; − 0;1; } 3 . 2 2 Câu 11.
Cho hai tập hợp A và B được mô tả bởi biểu đồ VEN sau đây
Khẳng định nào sau đây là đúng ?
A. B \ A = {1,2,7;9;1 } 1 .
B. A∩ B = {1;2;3;4; } 5 .
C. A∪ B = {3;4;5;7;9;1 } 1 .
D. A \ B = {3;4; } 5 .
Câu 12. Trong kì thi học sinh giỏi cấp trường, lớp 10 A có 15 học sinh thi học sinh giỏi môn Ngữ văn,
20 học sinh thi học sinh giỏi môn Toán. Tìm số học sinh thi cả hai môn Ngữ văn và Toán biết
lớp 10 A có 40 học sinh và có 10 học sinh không thi cả môn Toán và Ngữ văn. A. 6. B. 5. C. 4. D. 3.
Câu 13. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 2
2x + 3y > 0 B. 2 2
x + y < 2 C. 2
x + y ≥ 0
D. x + 3y > 7
Câu 14. Cho bất phương trình 2x + y < 6. Khẳng định nào sau đây là đúng?
A. Bất phương trình đã cho có nghiệm duy nhất.
B. Bất phương trình đã cho vô nghiệm.
C. Bất phương trình đã cho có vô số nghiệm.
D. Bất phương trình đã cho có tập nghiệm là ( ; −∞ 6)
Câu 15. Cặp số nào là một nghiệm của bất phương trình 5
− x − y > 6 ? A. ( 1; − 1) B. ( 3 − ;0) C. (1;3) D. (4; 2 − )
Câu 16. Miền nghiệm của bất phương trình 3x + 2y > 6 là y y y y 3 3 3 2 − A. B. C. D. O x 2 x 2 − O O x 2 − O x 3
Câu 17. Ông Hùng muốn mua x con gà giống và y con vịt giống để nuôi sao cho số tiền để mua không
vượt quá 700.000 đồng. Biết giá một con gà giống là 15.000 đồng, một con vịt giống là 20.000
đồng. Bất phương trình bậc nhất hai ẩn x và y thoả mãn điều kiện trên là
A. 3x + 4y ≥140 .
B. 3x + 4y ≤140 .
C. x + y ≤ 700.000 . D. 3x + 4y =140 .
Câu 18. Hệ bất phương trình nào sau đây không là hệ bất phương trình bậc nhất hai ẩn? 2 − x ≤ 0 x ≥ 0
4x − y ≥ 0 x + y ≥ 0 A. . B. . C. . D. . 5
x − 2y < 0 2
x − 2y ≥ 0
−x − 3y < 0
2x − y ≥ 0
Câu 19. Điểm O(0;0) không thuộc miền nghiệm của hệ bất phương trình nào sau đây? x + 3y < 0 x + 3y ≥ 0
x + 3y − 6 < 0
x + 3y − 6 < 0 A. . B. . C. . D. .
2x + y + 4 > 0
2x + y − 4 < 0
2x + y + 4 > 0
2x + y + 4 ≥ 0
Câu 20: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? y 3 2 x O y > 0 y > 0 x > 0 x > 0 A. . B. . C. . D. 3
x + 2y < 6 3
x + 2y < 6 − 3
x + 2y < 6 3
x + 2y > 6 −
Câu 21. Biểu thức F( ;
x y) = y − 2x đạt giá trị nhỏ nhất tại điểm M có toạ độ ( ;
x y) thuộc miền nghiệm
x − y −1 ≤ 0
của hệ bất phương trình x + 4y + 9 ≥ 0 . Tọa độ điểm M là
x − 2y +3 ≥ 0
A. (5;4) . B. ( 1; − 2 − ). C. ( 5; − − ) 1 . D. (5;1)
Câu 22. Cho góc tù. Điều khẳng định nào sau đây là đúng? A. cosα < 0 B. cot α > 0.
C. sin α < 0 . D. tan α > 0 .
Câu 23. Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ° 3 sin150 = − . B. ° 3 cos150 = . C. ° 1 tan150 = − . D. cot150° = 3 2 2 3
Câu 24. Trong các mệnh đề sau, mệnh đề sai là A. 0
cot(180 −α) = −cotα . B. 0
cos(180 −α) = −cosα . C. 0
tan(180 −α) = tanα . D. 0 sin(180 −α) = sinα .
Câu 25. Giá trị của sin 45° cos 45° + là: A. 1 B. 2 C. 2 D. 2 2 2
Câu 26. Giá trị của biểu thức 2 ° ° 3 2022 5sin 30 3cos60 tan 135° + − là: 4 A. 2 B. 5 3 1 + C. 2 − D. 5 3 1 − 2 2 2 2
Câu 27. Cho hình bình hành ABCD như hình vẽ bên dưới. Biết rằng 4
cosα = . Khi đó cos β bằng 5 D C α β A B A. 4 . B. 3 − . C. 4 − . D. 3 . 5 5 5 5 Câu 28. Cho 1 α + α
cotα = . Giá trị của biểu thức 3sin 4cos A = là: 3 2sinα − 5cosα A. 15 − . B. 13 − . C. 15 . D. 13. 13 13 Câu 29.
Cho tam giác ABC có BC = a , AC = b , AB = c . Mệnh đề nào sau đây đúng? 2 2 2 2 2 2 2 2 2 2 2 2 A. cos
a − b − c A + − + + + − = ⋅ B. cos b c a A = ⋅ C. cos b c a A = ⋅D. cos b c a A = ⋅ 2bc 2bc 2bc bc
Câu 30. Cho tam giác ABC với các kí hiệu thông thường. Kết luận nào sau đây sai? A. abc S = ⋅ B. 1
S = absin C ⋅ 4R 2
C. S = p( p − a)( p −b)( p − c) ⋅ D. 1
S = pr ⋅ 2
Câu 31. Cho tam giác ABC có góc ˆA 150° =
. Diện tích tam giác ABC là: A. 1 ab B. 1 bc C. 1 − ab D. 1 bc 4 4 2 2
Câu 32. Cho tam giác ABC có ˆ b 2 , m c 4 , m A 120° = = =
. Độ dài cạnh a là: A. 37 m B. 28 m C. 37 m D. 28m
Câu 33. Một mảnh đất hình tam giác có độ dài các cạnh là a = 3 3 c , m b = 6 c , m c = 3 cm. Diện tích mảnh đất là: A. 2 3 3 cm B. 2 9 3 cm C. 2 4,5 3 cm D. 2 5 3 cm
Câu 34. Bác An cần đo khoảng cách từ một địa điểm A trên bờ hồ đến một địa điểm B ở giữa hồ. Bác
sử dụng giác kế để chọn một điểm C cùng nằm trên bờ với A sao cho °
BAC 30 , ACB 100° = =
và AC = 50 m . Khoảng cách AB bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
A. 98,48 m.
B. 98,47 m .
C. 64,27 m .
D. 64,28 m . Câu 35.
Cho tam giác ABC có độ dài cạnh BC = 20 góc ˆA 120° =
.Bán kính đường tròn ngoại tiếp
tam giác ABC là:
A. R = 20 3 B. 20 R =
C. R = 20 D. 3 R = 3 2 2. Tự luận
Câu 1. (1,0 điểm)
a) Cho các tập hợp A ={0;1;2;3;4; }5 và B ={2;3;4;5; }6. Tìm các tập hợp A∪ B, A \ .B
b) Cho các tập hợp khác rỗng m + 3 A m 1; = − và B = ( ; −∞ 3
− ) ∪[3;+∞) . Gọi S 2 là tập hợp các giá
nguyên dương của m để A∩ B ≠ ∅ . Tìm số tập hợp con của S
Câu 2. (1,0 điểm)
a) Biểu diễn miền nghiệm của bất phương trình trình 3x + y ≥ 2 − .
b) Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại một cần 2kg nguyên liệu và 30 giờ, đem
lại mức lợi nhuận 40 000 đồng. Mỗi sản phẩm loại hai cần 4kg nguyên liệu và 15 giờ đem lại mức lợi
nhuận là 30 000 đồng. Xưởng có 200kg nguyên liệu và 1200 giờ làm việc. Hỏi cần sản xuất mỗi loại sản
phẩm bao nhiêu để có mức lợi nhuận cao nhất?
Câu 3.(1,0 điểm)
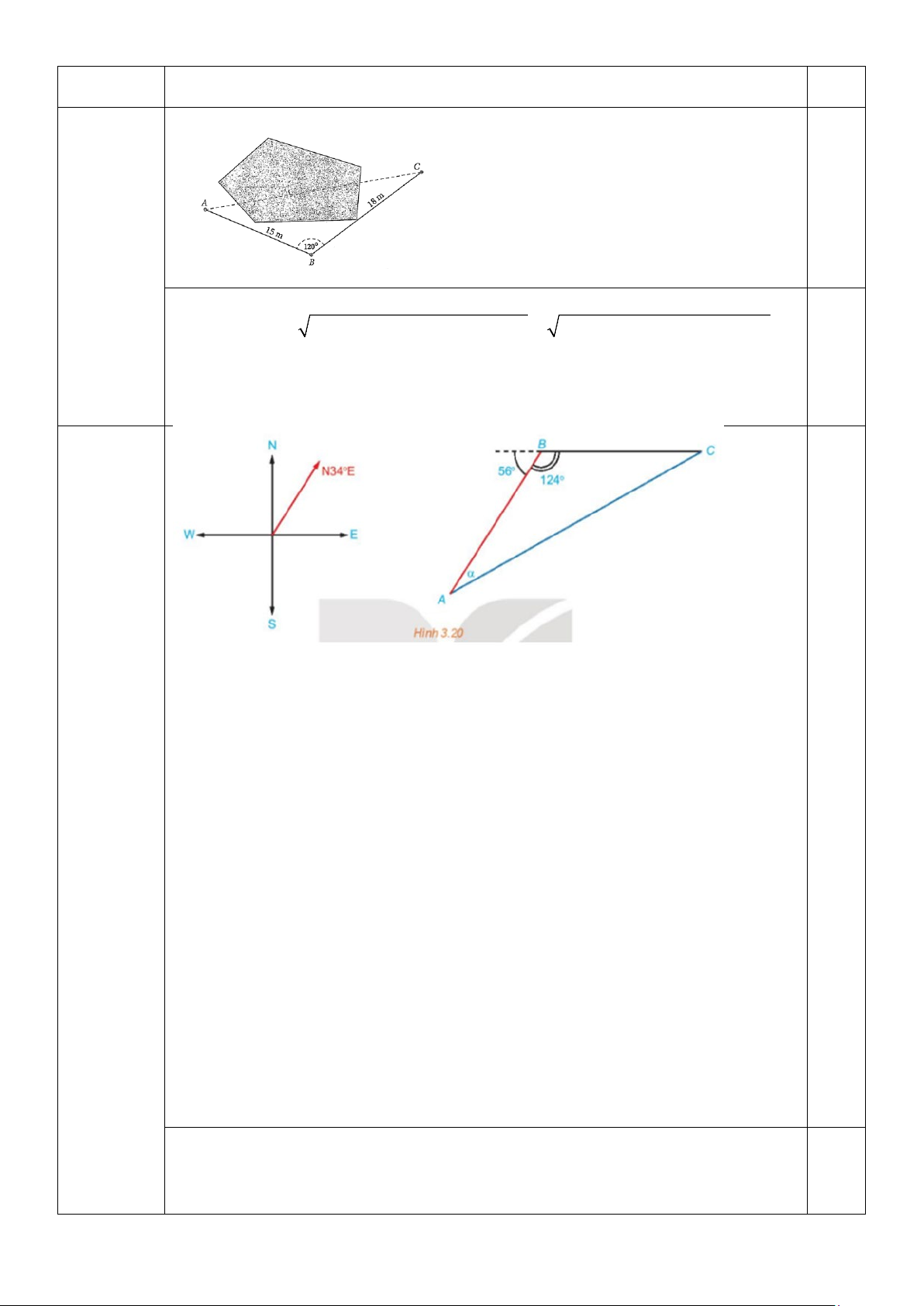
a) Để kéo dây điện từ cột điện vào nhà phải qua một cái ao, anh Nam không thể đo độ dài dây điện cần
mua trực tiếp được nên đã làm như sau: Lấy một điểm B như trong hình, người ta đo được độ dài từ B
đến A (nhà) là 15 m, từ B đến C (cột điện) là 18 m và ABC 120° =
. Hãy tính độ dài dây điện nối từ nhà ra đến cột điện.
b) Trên biển, tàu B ở vị trí cách tàu A 53 km về hướng 0
N34 E . Sau đó, tàu B chuyển động thẳng đều
với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn
50km/h để đuổi kịp tàu B. Hỏi tàu A cần phải chuyển động theo hướng nào và sau bao lâu tàu A đuổi kịp tàu B?
---------------Hết--------------
ĐÁP ÁN MÃ ĐỀ 101
1. TRẮC NGHIỆM (7,0 ĐIỂM). 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 A C B C A D B D C B C B D C B C B D
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 C B A C A B C A B A B D D A C C D 2. TỰ LUẬN (3,0 ĐIỂM). Câu Nội dung đáp án Điểm
Câu 1.a) a) A ={1;2;3; } 7 và B = {2;4;6;7; }
8 . Tìm các tập hợp A∪ B, A \ . B 0,25 (0,5 điểm) {
A∪ B = 1;2;3;4;6;7;8}.
A \ B = {1;3}. 0,25 Câu 1.b) Để A∩ B ≠ ∅ thì điều kiện là m + 3 (0,5 điểm) m −1< 2 m < 5 0,25 m −1 < 3 − ⇔ m < 2
− ⇔ m∈(−∞ − 2) ∪[3;5) . m+3 m ≥ ≥ 3 3 2 Vì *
m∈ ⇒ m∈{3; } 4 ⇒ S = {3; } 4 . 0,25
Số tập hợp con của S là 2 2 = 4 .
a) Vẽ đường thẳng (d ) :3x + 2y = 6. − . y 2 − O x 0,25 3
Câu 2.a) Lấy điểm O(0;0)∉d , ta có: 3.0+ 2.0 = 0 > 6. − (đúng) (0,5 điểm) 0,25
Ta thấy (0 ; 0) là nghiệm của bất phương trình đã cho.
Vậy miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa điểm O
(miền không bị gạch), kể cả d.
b) Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun
mẫu mới trong dịp tết này với số vốn đầu tư không quá 72 triệu đồng.
Loại dài tay giá mua vào 800.000 đồng và lãi 150.000 đồng 1 áo, loại
ngắn tay giá mua vào 600.000 đồng và lãi 120.000 đồng 1 áo. Cửa hàng
ước tính nhu cầu của khách không quá 100 cái cho cả 2 loại. Lập
phương án kinh doanh sao cho có lãi nhất.
Gọi x, y (x ≥ 0, y ≥ 0, x, y ∈) lần lượt là số áo dài tay và ngắn tay mà
cửa hàng nên mua để kinh doanh có lãi nhất. x ≥ 0 0,25
Câu 2.b) Theo yêu cầu bài toán, ta có hệ bất phương trình y ≥ 0 (*) x + y ≤100 (0,5 điểm) 8
x + 6y ≤ 720
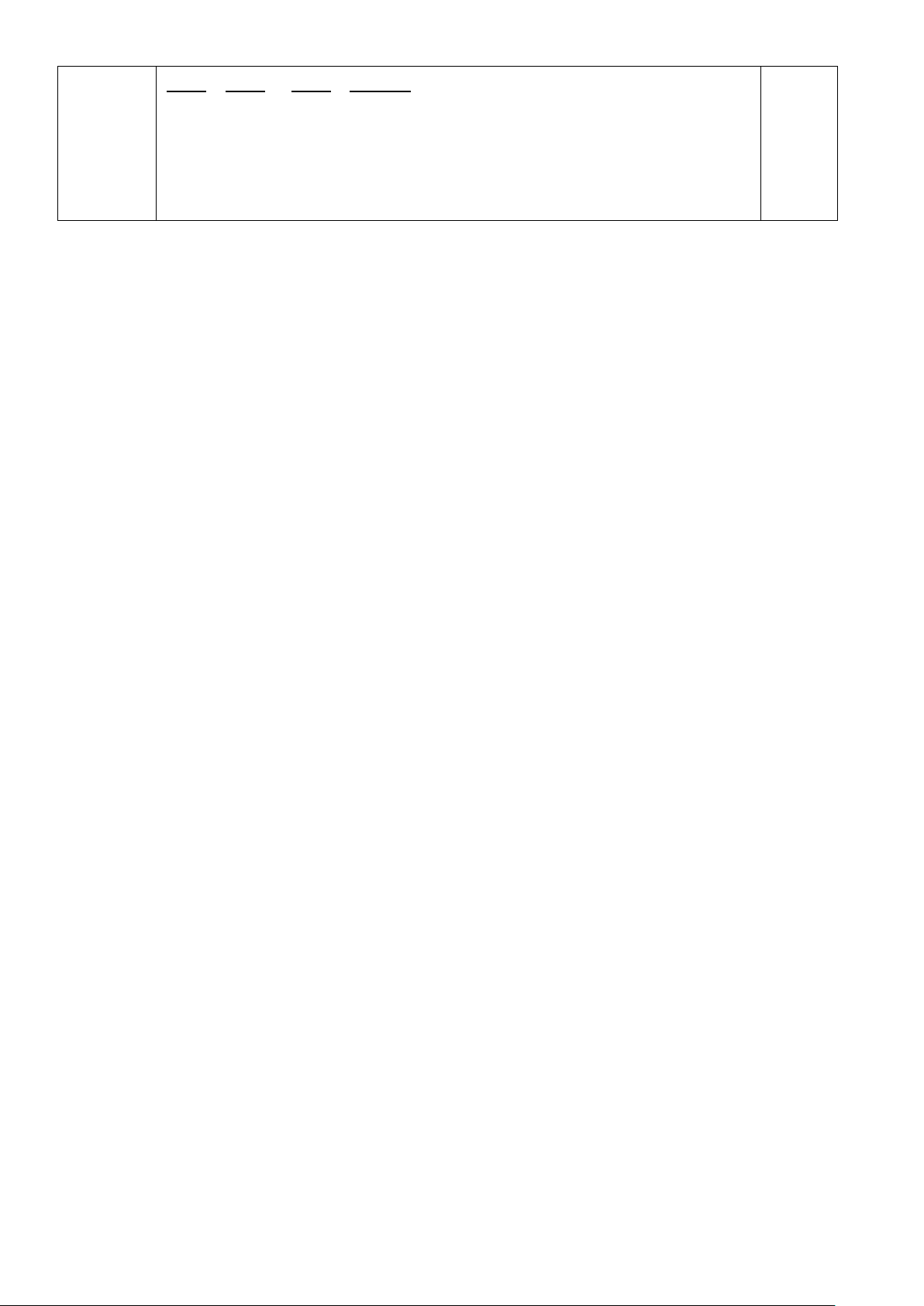
Ta cần tìm x, y để biểu thức F =150.000x +120.000y đạt GTLN trên miền nghiệm của (*)
Miền nghiệm là tứ giác OABC
Các điểm có tọa độ như sau: O(0;0) , (
A 0;100) , B(60;40), C(90;0)
Tại O(0;0) : F = 0 Tại (
A 0;100) : F =12.000.000
Tại B(60;40): F =13.800.000
Tại C(90;0): F =13.500.000 0.25
Vậy cửa hàng nên nhập 60 áo dài tay và 40 áo ngắn tay để kinh doanh
thì có lãi nhất và lãi thu được là 13.800.000 đồng. Xét A
∆ BC như hình vẽ, với AB =116 m; ˆ AC 218 , m A 30° = = . 0,25 Câu 3a (0,5 điểm)
Áp dụng Định lí côsin, ta có: 2 2 2
BC = AB + AC − 2AB ⋅ AC ⋅cos A 2 2
216 218 2.216.218.cos30o = + − ≈ 12621,19 0,25
Vậy khoảng cách giữa 2 diều là 112,35 m Câu 3b (0,5 điểm)
Gọi thời gian tàu A đuổi kịp tàu B ở vị trí C là x (h), với x > 0
Vì tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h đến C nên
quãng đường BC là 30x (km)
Vì tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu 0,25
B nên quãng đường AC là 50x (km) Xét ΔABC, có: 2 2 2
AC = BC + AB − 2A . B BC. os c B 2 2 2 0
⇔ 2500x = 900x + 53 − 2.53.30x. os c 124 2
⇔ 1600x −1778x − 2809 = 0 x ≈1,99 (t/m) ⇔ x ≈-0,88 (loai)
Do đó tàu A mất 1,99 giờ đuổi kịp tàu B. ⇒ BC = 30x = 59,7 AC = 50x = 99,5 0,25 Ta lại có: a b 59,7 99,5 = ⇒ = ⇒ 0 A 29,83 0 sin A sin B sin A sin124
⇒ AC hợp với phương nam một góc 0 0 0 34 + 29,83 = 63,83
Vậy tàu A chuyển động theo hướng N63,830E
ĐÁP ÁN MÃ ĐỀ 102
2. TRẮC NGHIỆM (7,0 ĐIỂM). 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 A B D D A C B C B B D B D C B A B B
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A A A A C C C A C D B D B D C D B 2. TỰ LUẬN (3,0 ĐIỂM). Câu Nội dung đáp án Điể m Câu 1.a)
a) Cho các tập hợp A ={0;1;2;3;4; }5 và B ={2;3;4;5; }6. Tìm các tập hợp (0,5 điểm) A∪ B, A \ . B 0,25 {
A∪ B = 0;1;2;3;4;6}. \ A B = {0;1}. 0,25 Câu 1.b) Để A∩ B ≠ ∅ thì điều kiện là m + 3 (0,5 điểm) m −1< 2 m < 5 0,25 m −1 < 3 − ⇔ m < 2
− ⇔ m∈(−∞ − 2) ∪[3;5) . m+3 m ≥ ≥ 3 3 2 Vì *
m∈ ⇒ m∈{3; } 4 ⇒ S = {3; } 4 . 0,25
Số tập hợp con của S là 2 2 = 4 .
a) Vẽ đường thẳng (d ) :3x + y = 2. − . 0,25
Câu 2.a) Lấy điểm O(0;0)∉d , ta có: 3.0 + 0 = 0 > 2. − (đúng) (0,5 điểm) 0,25
Ta thấy (0 ; 0) là nghiệm của bất phương trình đã cho.
Vậy miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa điểm O
(miền không bị gạch), kể cả d.
b) ) Gọi x (x ≥ 0) là số kg loại một cần sản xuất,
y ( y ≥ 0) là số kg loại hai cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x + 4y, thời gian là 30x +15y có mức lợi
nhuận là 40000x + 30000 . y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 1200 giờ làm việc,
suy ra 2x + 4y ≤ 200 hay x + 2y −100 ≤ 0;
30x +15y ≤1200 hay 2x + y −80 ≤ 0. 0,25
x + 2y −100 ≤ 0
2x + y −80 ≤ 0
Bài toán trở thành: Tìm ;
x y thoả mãn hệ (*) sao cho Câu 2.b) x ≥ 0 y ≥ 0 (0,5 điểm) L( ;
x y) = 40000x + 30000y đạt giá trị lớn nhất.
Biểu diễn miền nghiệm của hệ (*) là miền tứ giác OABC với
O(0;0), A(40;0), B(0;50),C (20;40). Ta có
L(0;0) = 0, L(40;0) =1600000,
L(0;50) =1500000, L(20;40) = 2000000.
Do đó giá trị lớn nhất của L( ;
x y) là 2 000 000 khi ( ; x y) = (20;40). 0.25
Vậy nên sản xuất 20kg sản phẩm loại một và 40kg sản phẩm loại hai để có mức lợi nhuận cao nhất. Xét A
∆ BC như hình vẽ, với = 15 ; = 18 ; ˆ =120o AB m BC m B Câu 3a 0,25 (0,5 điểm)
Áp dụng định lí côsin cho tam giác ABC ta có: 2 2 2 2 AC AB BC 2AB BC cos B 15 18 2 15 18 cos120° = + − ⋅ ⋅ = + − ⋅ ⋅ ⋅ ≈ 28 0,25
Vậy độ dài dây điện nối từ nhà ra cột điện dài 28,62 m. Câu 3b (0,5 điểm)
Gọi thời gian tàu A đuổi kịp tàu B ở vị trí C là x (h), với x > 0
Vì tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h đến C nên quãng đường BC là 30x (km)
Vì tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B 0,25
nên quãng đường AC là 50x (km) Xét ΔABC, có: 2 2 2
AC = BC + AB − 2A . B BC. os c B 2 2 2 0
⇔ 2500x = 900x + 53 − 2.53.30x. os c 124 2
⇔ 1600x −1778x − 2809 = 0 x ≈1,99 (t/m) ⇔ x ≈-0,88 (loai)
Do đó tàu A mất 1,99 giờ đuổi kịp tàu B. ⇒ BC = 30x = 59,7 0,25 AC = 50x = 99,5 Ta lại có: a b 59,7 99,5 = ⇒ = ⇒ 0 A 29,83 0 sin A sin B sin A sin124
⇒ AC hợp với phương nam một góc 0 0 0 34 + 29,83 = 63,83
Vậy tàu A chuyển động theo hướng N63,830E