










Preview text:
SỞ GIÁO DỤC &ĐÀO TẠO PHÚ
THI GIỮA HỌC KỲ I THỌ MÔN THI: TOÁN Năm học 2025-2026
TRƯỜNG THPT NAM LƯƠNG SƠN
Thời gian làm bài : 90 phút Đề chính thức
(Đề thi có 3 trang) Mã đề: 101
Họ tên :............................................................... Số báo danh : ...............................................................
PHẦN I. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu
12. Mỗi câu hỏi học sinh chỉ chọn một phương án. Câu 1:
Góc có số đo π đổi sang độ là: 24 A. 0 8 . B. 0 8 30 .′ C. 0 7 . D. 0 7 30 .′
Câu 2: Trong các công thức sau, công thức nào đúng? + A. ( − ) tan a tan tan b a b = .
B. tan (a – b) = tan a − tan . b 1− tan a tan b + C. ( + ) tan a tan tan b a b = .
D. tan (a + b) = tan a + tan . b 1− tan a tan b
Câu 3: Tập xác định của hàm số y = cot x là: A. π \ kπ ,k + ∈ .
B. \{k2π,k ∈ } . 2 C. π \ k2π ,k + ∈ .
D. \{kπ,k ∈ } . 2
Câu 4: Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép nhóm sau:
Giá trị đại diện của nhóm [30;40) là: A. 40 . B. 9. C. 35. D. 30. u
Câu 5: Cho cấp số nhân (u , biết u =12 , 3 = 243 . Tìm u . n ) 1 u 9 8 4 4 2 A. u = u = u = 9 . B. . C. u = 78732 . D. . 6563 9 2187 9 9 2187 + Câu 6: Cho dãy số ( n u với 1 u = . Tính u . n ) n n 3 A. 5 . B. 5. C. 4 . D. 6 . 4 3 5 Câu 7:
Nghiệm của phương trình 1 cos x là 2 A. x
k2
B. x k2
C. x k D. 2 x k2 6 3 6 3
Câu 8: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở
bảng sau (đơn vị: triệu đồng) Nhóm chứa trung vị là Mã đề: 101 Trang 1/3 A. [7;9) . B. [9;1 ) 1 . C. [13;15). D. [11;13) .
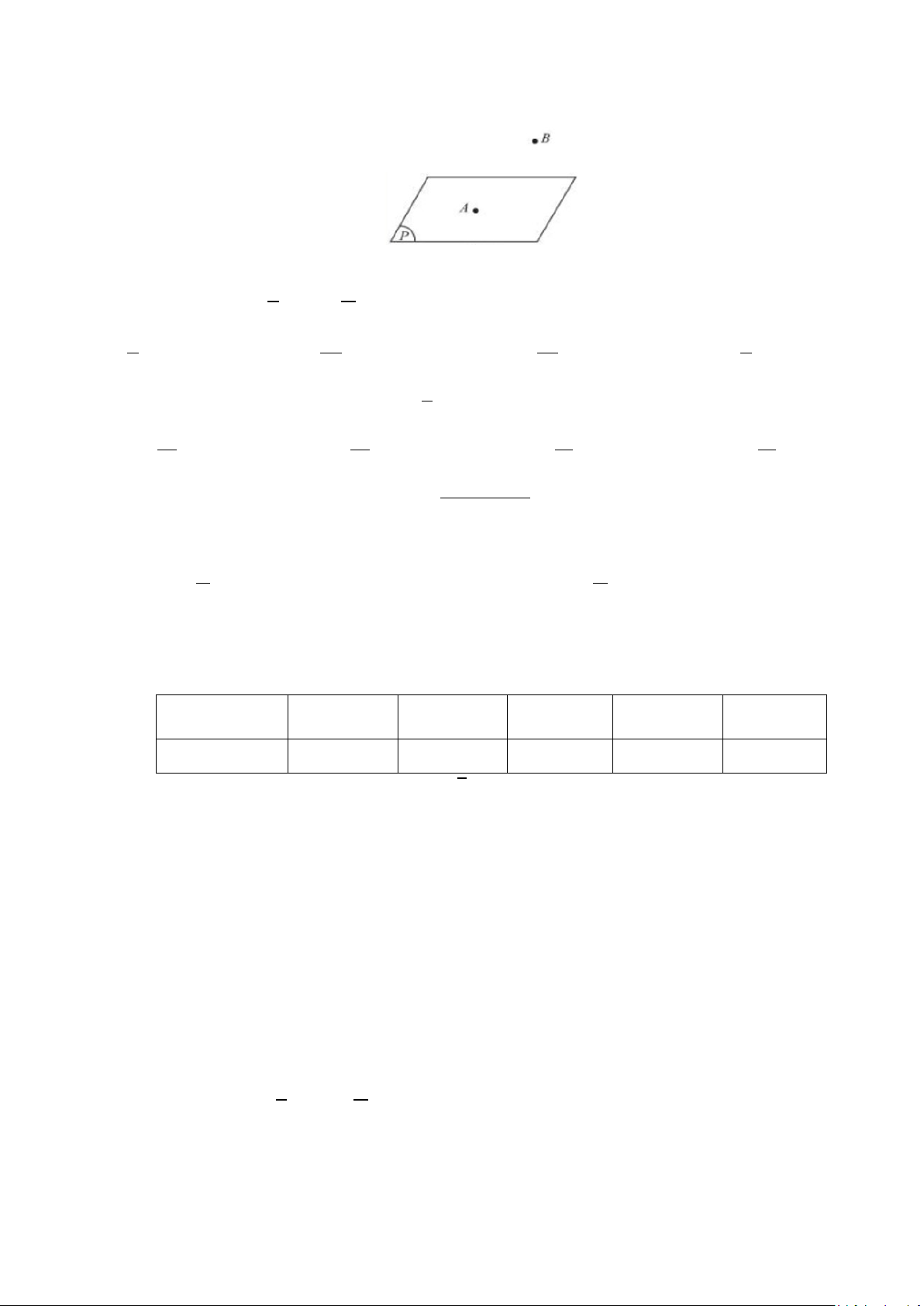
Câu 9: Cho hai điểm ,
A B và mặt phẳng (P) như hình vẽ bên dưới. Khẳng định nào sau đây đúng?
A. A ⊂ (P).
B. A∈ (P).
C. B ∈ (P).
D. B ⊄ (P). π Câu 10: Cho 4 cos x , x ;0 = ∈ −
. Giá trị của sin 2x là 5 2 A. 1 . B. 24 . C. 24 − . D. 1 − . 5 25 25 5
Câu 11: Cho một cấp số cộng (u có 1
u = , u = 26. Tìm công sai d n ) 1 3 8 A. 3 d = . B. 10 d = . C. 11 d = . D. 3 d = . 10 3 3 11
Câu 12: Tìm tập xác định D của hàm số 1 y = . sin x − cos x
A. D = \{k2π | k ∈ } .
B. D = \{kπ | k ∈ } . C. π π D \ kπ | k = + ∈ .
D. D = \ + kπ | k ∈ . 4 2
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a),
b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).
Câu 1: Kết quả đo chiều cao (đơn vị: mét) của 100 cây keo 3 năm tuổi tại một nông trường được cho ở bảng sau:
Chiều cao (m) [8,4;8,6) [8,6;8,8) [8,8;9,0) [9,0;9,2) [9,2;9,4) Số cây 5 12 25 44 14
a) Số trung bình của mẫu số liệu ghép nhóm là x = 8,9(m) .
b) Mẫu số liệu ghép nhóm trên có 5 nhóm số liệu.
c) Hiệu giữa tứ phân vị thứ ba và tứ phân vị thứ nhất bằng 2,06 .
d) Số cây keo có chiều cao khoảng 9,1(m) là nhiều nhất.
Câu 2: Cho cấp số cộng (u biết số hạng đầu u = 2 và công sai d = 3. n ) 1
Các mệnh đề sau đúng hay sai?
a) Đặt S = u + u +...+ u + u + u +...+ u + u + u +...+ u . Khi đó S = 7372 . 10 11 20 30 31 50 60 61 80
b) Số 610 là tổng của n số hạng đầu của cấp số cộng (u . Khi đó n∈[18;22]. n )
c) Số 152 là số hạng thứ n của cấp số cộng (u . Khi đó n∈[45;50] . n )
d) Số hạng tổng quát của cấp số cộng là u = − + n . n 1 3
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4. π Câu 1: Cho biết 3
cosα = ,0 < α < . Giá trị sinα bằng bao nhiêu? 5 2
Câu 2: Chị Nụ gửi tiết kiệm 200 triệu đồng với lãi suất 0,5% một tháng. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẻ được nhập vào vốn ban đầu. Hỏi số tiền chị Nụ
nhận được sau hai tháng là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị) Mã đề: 101 Trang 2/3
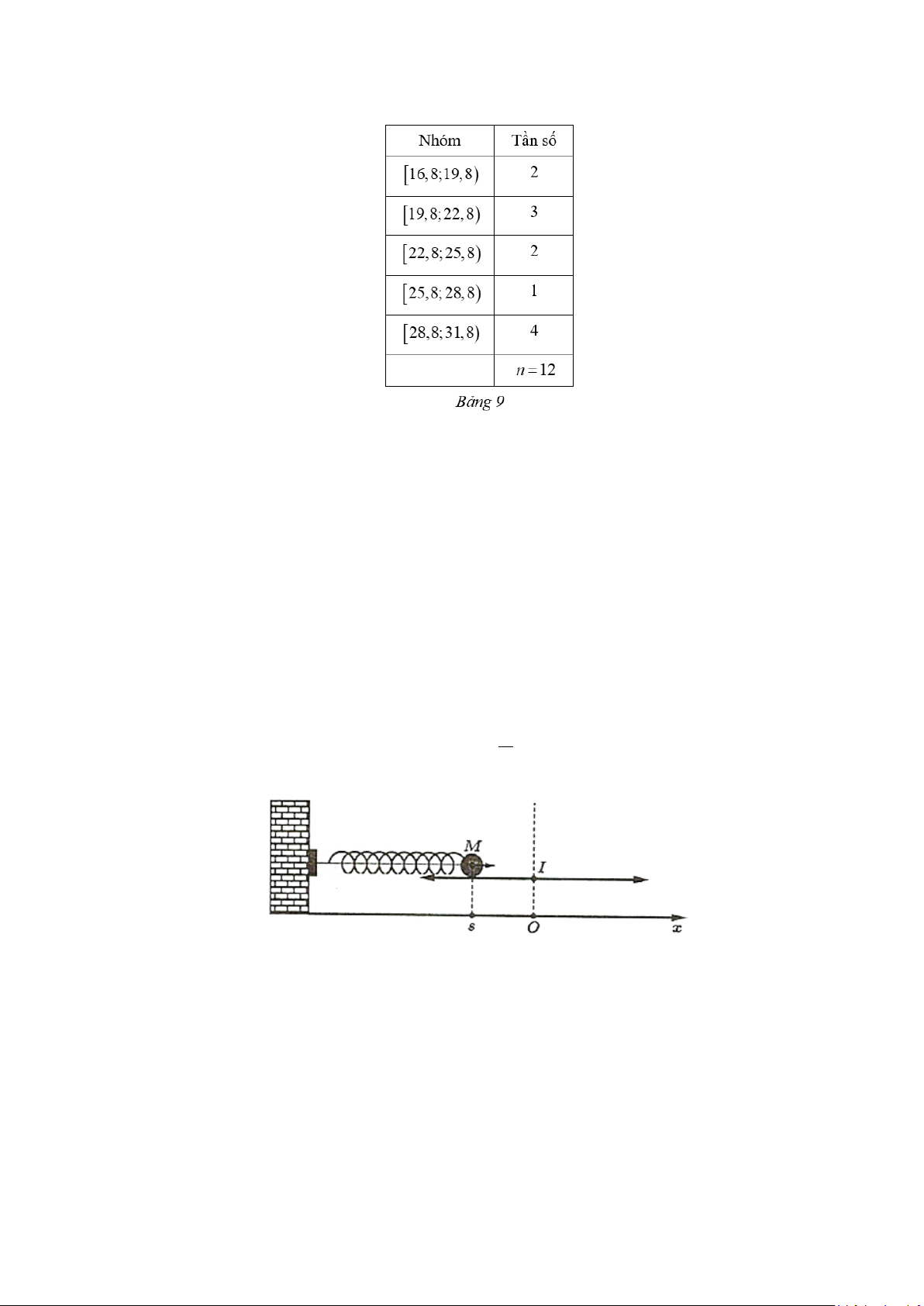
Câu 3: Bảng 9 biểu diễn mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình các tháng năm 2011
tại Hà Nội (đơn vị: độ C) (Nguồn: Niên giám Thống kê 2021, NXB Thống kê, 2022). Số trung bình cộng
của mẫu số liệu đó bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)? u =10
Câu 4: Tính tổng của số hạng đầu u1 và công sai d của cấp số cộng (u biết rằng: 4 n ) u +u = 26 4 6
PHẦN IV. (3,0 điểm).Tự luận
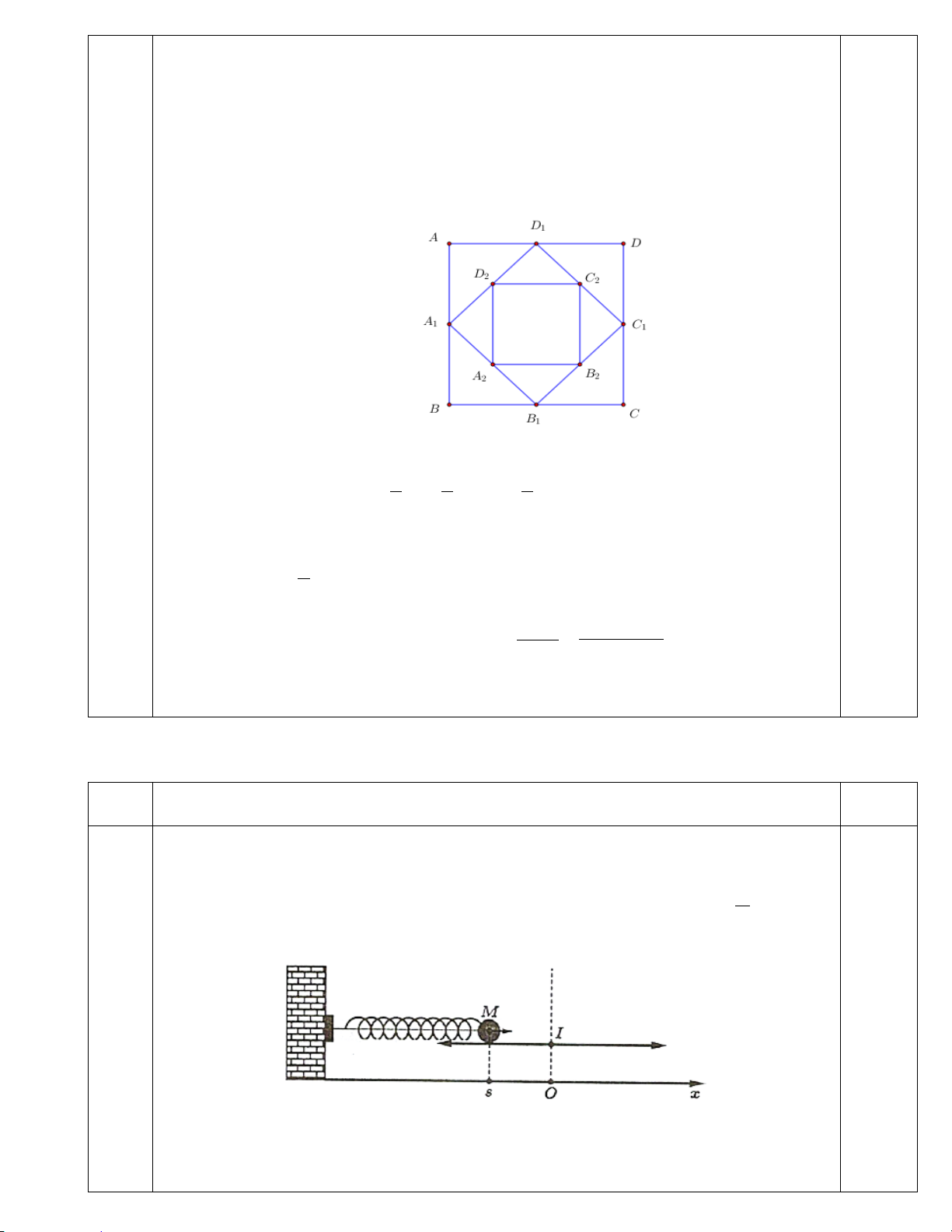
Câu 1: Cho hình vuông ABCD có cạnh bằng 4 và có diện tích S A B C D
1 . Nối 4 trung điểm 1 , 1 , 1 , 1
theo thứ tự của 4 cạnh AB , BC , CD , DA ta được hình vuông thứ hai có diện tích S2 . Tiếp tục làm
như thế, ta được hình vuông thứ ba là A B C D S
2 2 2 2 có diện tích 3 , …và cứ tiếp tục làm như thế, ta tính
được các hình vuông lần lượt có diện tích S S S
S = S + S + S +...+ S
4 , 5 ,…, 100 . Tính tổng 1 2 3 100 .
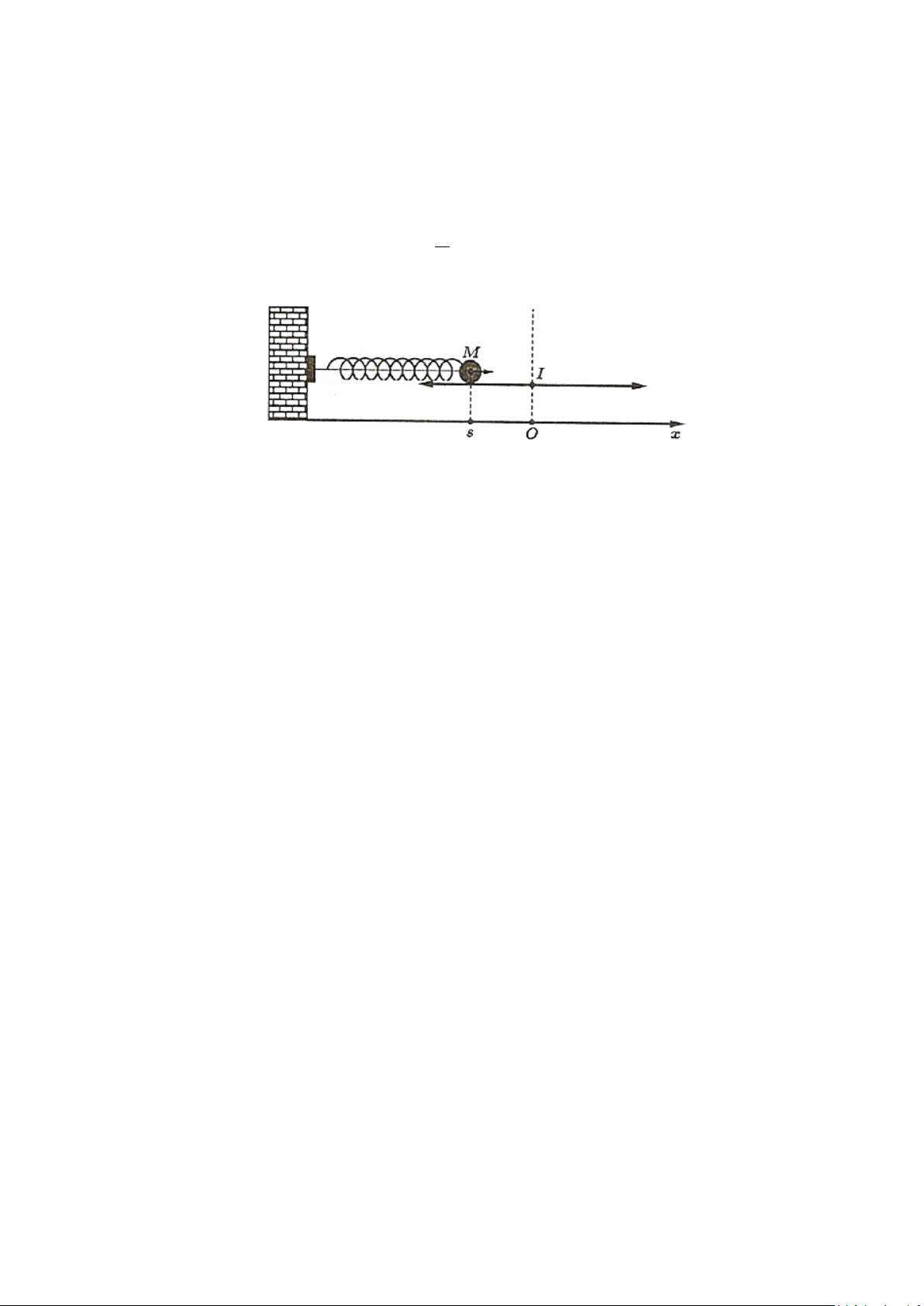
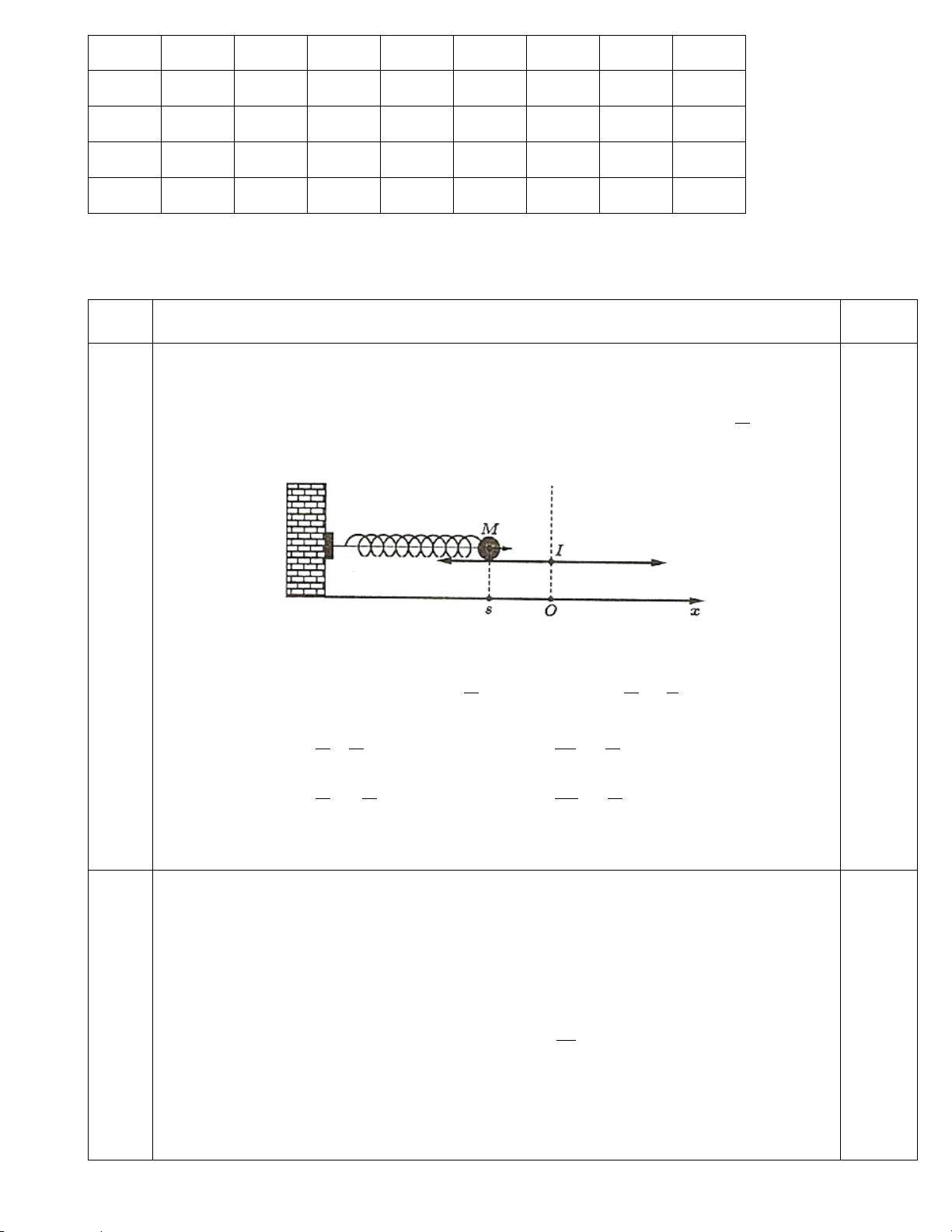
Câu 2: Một vật M được gắn vào đầu lò xo và dao động quanh vị trí cân bằng I , biết rằng O là hình
chiếu vuông góc của I trên trục Ox , toạ độ điểm M trên Ox tại thời điểm t (giây) là đại lượng s (đơn vị: π
cm ) được tính bởi công thức s 8,6cos 8t = +
. Tại mấy thời điểm trong khoảng 2 giây đầu 2
tiên thì s = 4,3 cm?
Câu 3: Bánh xe của người đi xe đạp quay được 10 vòng trong 5 giây. Tính độ dài quãng đường mà người đi
xe đã đi được trong 1 phút( đơn vị tính bằng mét và làm tròn kết quả đến hàng đơn vị, lấy π = 3,14 ),
biết rằng đường kính của bánh xe đạp là 0,68m. Hết Mã đề: 101 Trang 3/3
SỞ GIÁO DỤC& ĐÀO TẠO PHÚ
THI GIỮA HỌC KỲ I THỌ MÔN THI: TOÁN Năm học 2025-2026
TRƯỜNG THPT NAM LƯƠNG SƠN
Thời gian làm bài : 90 phút Đề chính thức
(Đề thi có 3 trang) Mã đề: 201
Họ tên :............................................................... Số báo danh : ...............................................................
PHẦN I. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu
12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1: Tìm tập xác định D của hàm số 1 y = . sin x − cos x A. π D \ kπ | k = + ∈ .
B. D = \{k2π | k ∈ } 2 . C. D = π
\{kπ | k ∈ } . D. D \ kπ | k = + ∈ . 4 Câu 2: Cho π tanα = 2 . Tính tan α − . 4 A. 1. B. 1 . C. 2 . D. 1 − . 3 3 3
Câu 3: Tập xác định của hàm số y = 2sin x là A. [0;2] . B. [ 1; − ] 1 . C. . D. [ 2; − 2].
Câu 4: Trong các công thức sau, công thức nào đúng?
A. cos(a + b) = cos . a cosb + sin . a sin b .
B. sin (a −b) = sin . a cosb − cos . a sin b .
C. cos(a −b) = cos . a sin b + sin . a sin b .
D. sin (a + b) = sin . a cosb − cos . a sin b .
Câu 5: Cho dãy số ( u ) với u = − . Mệnh đề nào sau đây đúng? n ( 5)n n A. u = 20 − . B. u = 625 − . C. u = 20. D. u = 625 . 4 4 4 4
Câu 6: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút)
[0;20) [20;40) [40;60) [60;80) [80;100) Số học sinh 5 9 12 10 6
Giá trị đại diện của nhóm [20;40) là A. 20 . B. 30. C. 10. D. 40 .
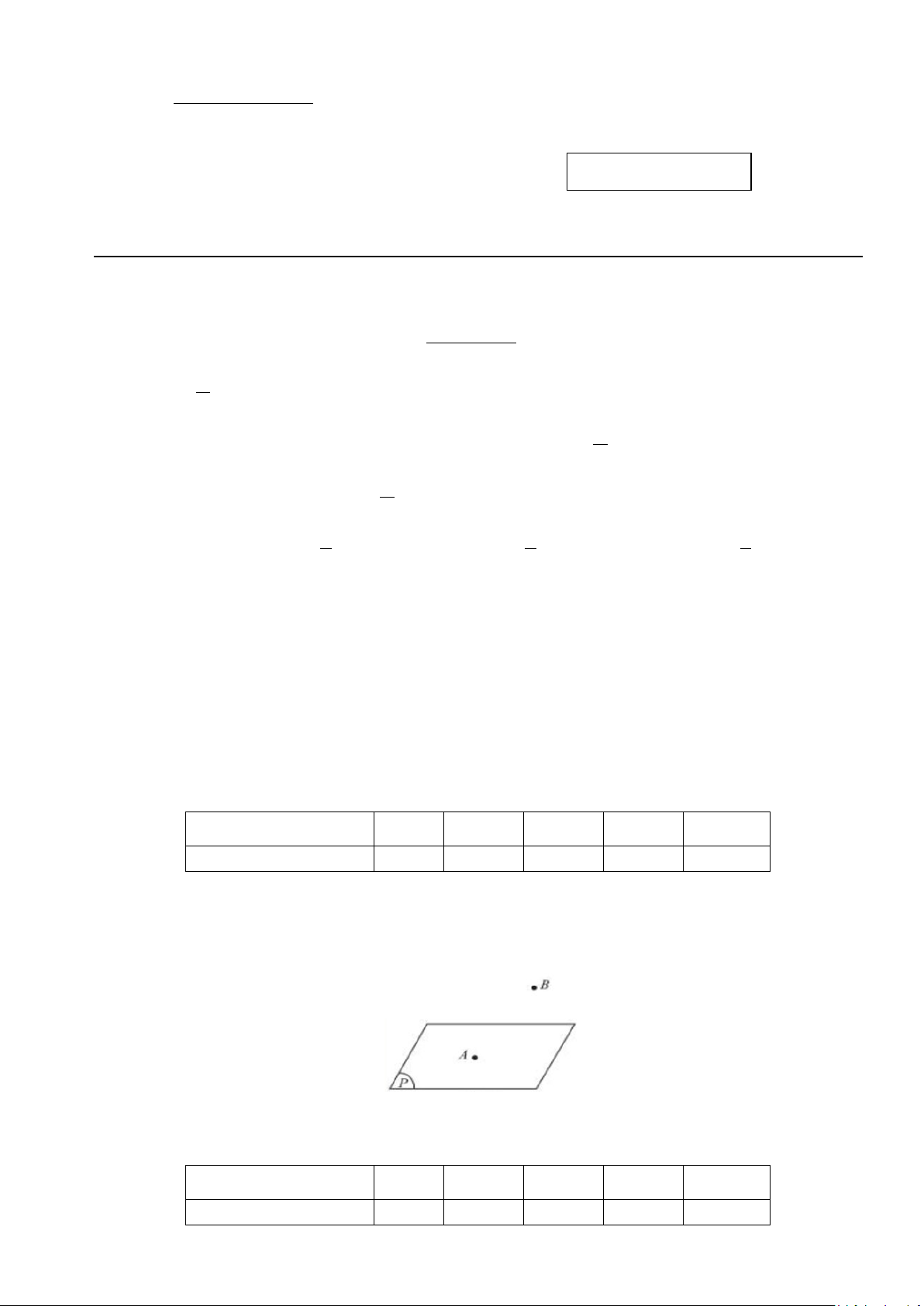
Câu 7: Cho hai điểm ,
A B và mặt phẳng (P) như hình vẽ bên dưới. Khẳng định nào sau đây đúng?
A. B ⊄ (P).
B. A ⊂ (P).
C. B ∈ (P).
D. A∈ (P).
Câu 8: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút)
[0;20) [20;40) [40;60) [60;80) [80;100) Số học sinh 5 9 12 10 6 Mã đề: 201 Trang 1/3 Nhóm chứa trung vị là A. [20;40) . B. [60;80) . C. [40;60). D. [0;200). Câu 9: Góc có số đo 0 120 đổi sang rađian là: A. 3π . B. 2π . C. π . D. π . 2 3 10 4
Câu 10: Phương trình 3 sin x = có nghiệm là: 2 x π = + k2π x π = + kπ A. π π x = ± + k2π . B. 3 . C. 6 .
D. x = + kπ . 3 2 x π = + k2 5π 3 3 π x = 6 + kπ
Câu 11: Cho cấp số cộng (u u = 2 u = 6 n ) với 1 và 2
. Công sai của cấp số cộng đã cho là A. 4 − . B. 4 . C. 3. D. 8. u
Câu 12: Cho cấp số nhân (u , biết u =12 , 3 = 243 . Tìm u . n ) 1 u 9 8 4 2 4 A. u = u = u = 9 . B. . C. u = 78732 . D. . 6563 9 2187 9 9 2187
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a),
b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).
Câu 1: Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng ,
A B được cho ở bảng sau: Cân nặng (gam)
[150;155) [155;160) [160;165) [165;170) [170;175)
Số quả cam ở lô hàng A 2 6 12 4 1
Số quả cam ở lô hàng B 1 3 7 10 4
a) Nhóm chứa mốt của số liệu ở lô hàng A là [155;160) .
b) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A .
c) Nhóm chứa mốt của số liệu ở lô hàng B là [160;165) .
d) Giá trị đại diện nhóm [150;155) bằng 152,5
Câu 2: Cho cấp số cộng ( 3 1
u có số hạng đầu u = , công sai d = . Khi đó các mệnh đề dưới đây n ) 1 2 2 đúng hay sai:
a) Số 5 là số hạng thứ 8 của cấp số cộng đã cho.
b) Số 15 là một số hạng của cấp số cộng đã cho. 4
c) Công thức số hạng tổng quát của cấp số cộng đã cho là n u = 1+ . n 3
d) Tổng 100 số hạng đầu của cấp số cộng (u trên bằng 2620 . n )
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1: Cho mẫu số liệu ghép nhóm về thống kê huyết áp của 20 người, ta có bảng số liệu sau:
Tìm trung vị của mẫu số liệu ghép nhóm trên (Kết quả làm tròn đến hàngđơn vị ). π Câu 2: Cho biết 3
sinα = , < α < π .Giá trị cosα bằng bao nhiêu? 5 2 u − u = 20
Câu 3: Tính tổng của số hạng đầu u1 và công sai d của cấp số cộng (u biết rằng: 3 1 n ) u +u = 54 2 5 Mã đề: 201 Trang 2/3
Câu 4: Chị Hoa gửi tiết kiệm 300 triệu đồng với lãi suất 0,5% một tháng. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẻ được nhập vào vốn ban đầu. Hỏi số tiền chị Hoa
nhận được sau hai tháng là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị)
PHẦN IV. (3,0 điểm).Tự luận Câu 1:
Một vật M được gắn vào đầu lò xo và dao động quanh vị trí cân bằng I , biết rằng O là hình chiếu
vuông góc của I trên trục Ox , toạ độ điểm M trên Ox tại thời điểm t (giây) là đại lượng s (đơn vị: π
cm ) được tính bởi công thức s 4,8cos 8t = +
. Tại mấy thời điểm trong khoảng 2 giây đầu tiên thì 2 s = 2,4cm?
Câu 2: Cho hình vuông ABCD có cạnh bằng 4 và có diện tích S A B C D
1 . Nối 4 trung điểm 1 , 1 , 1 , 1
theo thứ tự của 4 cạnh AB , BC , CD , DA ta được hình vuông thứ hai có diện tích S2 . Tiếp tục làm
như thế, ta được hình vuông thứ ba là A B C D S
2 2 2 2 có diện tích 3 , …và cứ tiếp tục làm như thế, ta tính
được các hình vuông lần lượt có diện tích S S S
S = S + S + S +...+ S
4 , 5 ,…, 100 . Tính tổng 1 2 3 100 .
Câu 3: Bánh xe của người đi xe đạp quay được 15 vòng trong 5 giây. Tính độ dài quãng đường mà
người đi xe đã đi được trong 1 phút( đơn vị tính bằng mét và làm tròn kết quả đến hàng đơn vị, lấy
π = 3,14 ), biết rằng đường kính của bánh xe đạp là 0,68m. Hết Mã đề: 201 Trang 3/3
SỞ GD&ĐT PHÚ THỌ
ĐÁP ÁN ĐỀ THI GIỮA KÌ 1
TRƯỜNG THPT NAM LƯƠNG SƠN
NĂM HỌC 2025 – 2026 Môn: TOÁN - LỚP 11 PHẦN I
(Mỗi câu trả lời đúng thí sinh được 0,25 điểm) 201 202 203 204 Mã đề 101 102 103 104 D D C D 1 D A D A B A C C 2 C D A D C B A C 3 D A D C B C D C 4 C D D B D A D D 5 B C B D B C C D 6 C C B D D C C A 7 D C A B C A A A 8 B D B A B D B D 9 B C B A B A C C 10 C B B B B D A C 11 C A B D D D A A 12 C B B D PHẦN II
Điểm tối đa của 01 câu hỏi là 1 điểm.
Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
Thí sinh lựa chọn chính xác cả 04 ý trong 1 câu hỏi được 1 điểm. 201 202 203 204 Mã đề 101 102 103 104 SĐSĐ SSSĐ ĐĐSS SĐĐS 1 SĐSĐ SĐĐS
SĐĐĐ ĐSĐĐ ĐSSS SSĐĐ SSSĐ SSĐS 2 ĐĐSĐ ĐĐĐS SĐSĐ ĐSSĐ PHẦN III
(Mỗi câu trả lời đúng thí sinh được 0,5 điểm) 201 202 203 204 Mã đề 101 102 103 104 0,8 24,8 24,8 0,8 102 -0,8 -0,8 12 1 202 202 0,8 4 -0,8 102 102 303 2 24,8 4 202 24,8 12 303 12 102 3 4 0,8 4 202 303 12 303 -0,8 4
PHẦN IV. Tự Luận (3 điểm):
Mã đề: 101;102;103;104 Câu Nội dung Điểm
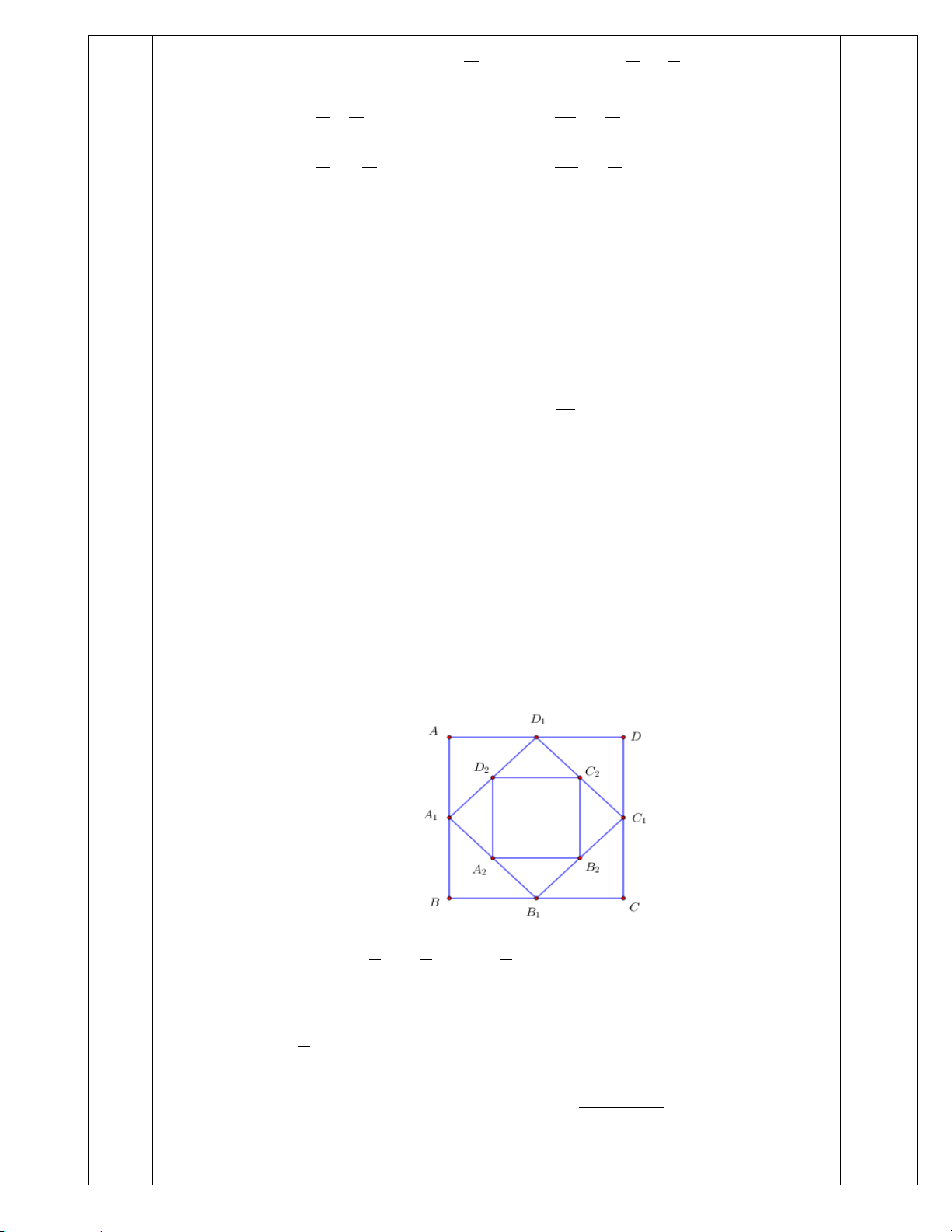
Câu 1 Một vật M được gắn vào đầu lò xo và dao động quanh vị trí cân bằng I , biết rằng O là
hình chiếu vuông góc của I trên trục Ox , toạ độ điểm M trên Ox tại thời điểm t (giây) là đại lượng π
s (đơn vị: cm ) được tính bởi công thức s 8,6cos 8t = + . Tại 2
mấy thời điểm trong khoảng 2 giây đầu tiên thì s = 4,3 cm? Lời giải Khi s = 4,3 thì π π 1 8,6cos 8t + = 4,3 ⇒ cos8t + = 2 2 2 0,5 π π π π 8t + = + k2π t = − + k 2 3 48 4 ⇔ (k ∈) ⇔ (k ∈). π π 5π π 0,5
8t + = − + k2π t = − + k 2 3 48 4
Câu 2 Bánh xe của người đi xe đạp quay được 10 vòng trong 5 giây. Tính độ dài quãng đường
mà người đi xe đã đi được trong 1 phút( đơn vị tính bằng mét và làm tròn kết
quả đến hàng đơn vị, lấy π = 3,14 ), biết rằng đường kính của bánh xe đạp là 0,68m. Lời giải 0,25
Chu vi bánh xe: C = π.d = 3,14.0,68(m) 10
Trong 1 giây bánh xe quay được số vòng: = 2 0,25 5
Số vòng bánh xe quay được trong 1 phút là: 60.2 =120 (vòng) 0,25
Vậy quãng đường mà người đi xe đã đi được trong 1 phút là:
S = 3,14.0,68.120 ≈ 256(m) 0,25
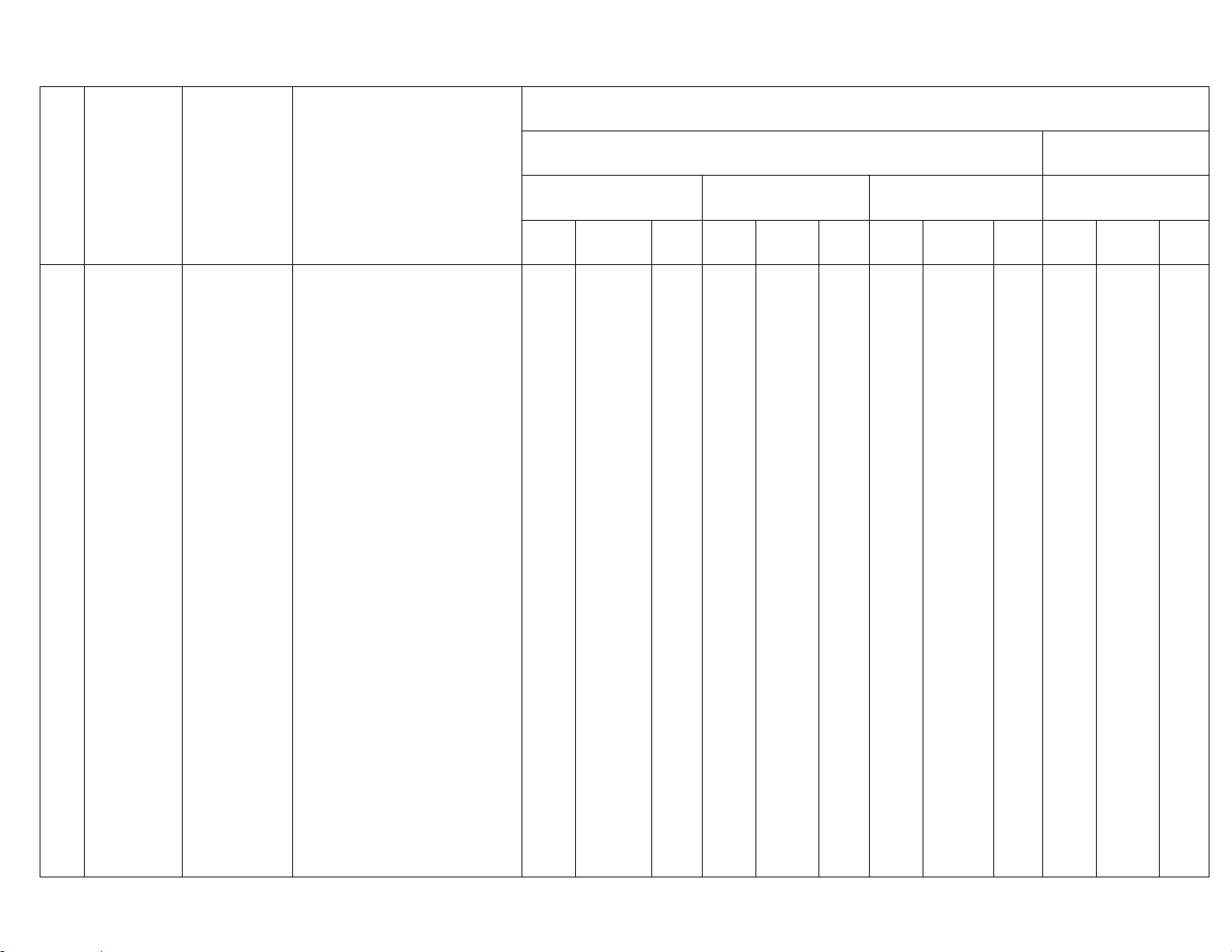
Câu 3 Cho hình vuông ABCD có cạnh bằng 4 và có diện tích S A B C
1 . Nối 4 trung điểm 1 , 1 , 1 , D
1 theo thứ tự của 4 cạnh AB , BC , CD , DA ta được hình vuông thứ hai có diện tích S A B C D
2 . Tiếp tục làm như thế, ta được hình vuông thứ ba là 2 2 2 2 có diện tích S
3 , …và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích S S S
S = S + S + S +...+ S
4 , 5 ,…, 100 . Tính tổng 1 2 3 100 . Lời giải 1 1 1 0,5 Ta có 2
S = 4 S = 4 = S S = .S 1 ; 2 2 1 ; ,… 2 2 3 2 2 Do đó S S S S u = S = 4
1 , 2 , 3 ,…, 100 là cấp số nhân với số hạng đầu 2 1 1 và công 0,25 1 bội q = . 2 n 2 4 ( 100 2 − ) 1
Suy ra S = S + S + S +...+ S 1− q = = 1 2 3 100 = S . 32 . 1 1− q 99 2 0,25
Mã đề: 201;202;203;204 Câu Nội dung Điểm
Câu 1 Một vật M được gắn vào đầu lò xo và dao động quanh vị trí cân bằng I , biết rằng O là
hình chiếu vuông góc của I trên trục Ox , toạ độ điểm M trên Ox tại thời điểm t (giây) là đại lượng π
s (đơn vị: cm ) được tính bởi công thức s 4,8cos 8t = + . Tại 2
mấy thời điểm trong khoảng 2 giây đầu tiên thì s = 2,4cm? Lời giải 0,5 Khi s = 2,4 thì π π 1 4,8cos 8t + = 2, 4 ⇒ cos8t + = 2 2 2 π π π π 8t + = + k2π t = − + k 0,5 2 3 48 4 ⇔ (k ∈) ⇔ (k ∈). π π 5π π
8t + = − + k2π t = − + k 2 3 48 4
Câu 2 Bánh xe của người đi xe đạp quay được 15 vòng trong 5 giây. Tính độ dài quãng đường
mà người đi xe đã đi được trong 1 phút( đơn vị tính bằng mét và làm tròn kết
quả đến hàng đơn vị, lấy π = 3,14 ), biết rằng đường kính của bánh xe đạp là 0,68m. Lời giải 0,25
Chu vi bánh xe: C = π.d = 3,14.0,68(m) 0,25 15
Trong 1 giây bánh xe quay được số vòng: = 3 5 0,25
Số vòng bánh xe quay được trong 1 phút là: 60.3 =180 (vòng)
Vậy quãng đường mà người đi xe đã đi được trong 1 phút là: 0,25
S = 3,14.0,68.180 ≈ 384(m)
Câu 3 Cho hình vuông ABCD có cạnh bằng 4 và có diện tích S A B C
1 . Nối 4 trung điểm 1 , 1 , 1 , D
1 theo thứ tự của 4 cạnh AB , BC , CD , DA ta được hình vuông thứ hai có diện tích S A B C D
2 . Tiếp tục làm như thế, ta được hình vuông thứ ba là 2 2 2 2 có diện tích S
3 , …và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích S S S
S = S + S + S +...+ S
4 , 5 ,…, 100 . Tính tổng 1 2 3 100 . Lời giải 1 1 1 Ta có 2
S = 4 S = 4 = S S = .S 1 ; 2 2 1 ; ,… 2 2 3 2 2 0,5 Do đó S S S S u = S = 4
1 , 2 , 3 ,…, 100 là cấp số nhân với số hạng đầu 2 1 1 và công 1 bội q = . 0,25 2 n 2 4 ( 100 2 − ) 1
Suy ra S = S + S + S +...+ S 1− q = = 1 2 3 100 = S . 32 . 1 1− q 99 2 0,25
MA TRẬN ĐỀ GIỮA HỌC KÌ I – MÔN TOÁN 11 – NĂM HỌC 2025-2026
Mức độ đánh giá Tỉ Nội TNKQ Tự luận Tổng lệ Chương/ dung/đơn TT Nhiều lựa chọn Đúng - Sai Trả lời ngắn % chủ đề vị kiến thức điể Hiể Hiể Hiể
Biết Hiểu VD Biết Hiểu VD Biết VD Biết VD Biết VD m u u u Giá trị lượng giác 11, 1 1 1 1 1 1 của góc 5% lượng giác
Hàm số lượng Công thức 7,7 1 giác và lượng giác 1 1 1 1 % phương trình lượng giác Hàm số 3,8 1 1 lượng giác % Phương 11, trình 1 1 1 1 2 5% lượng giác 3,8 Dãy số 1 1 % Dãy số. cấp số 23,
cộng và cấp số Cấp số 1 1 2 1 1 2 2 2 2 nhân cộng 1% Cấp số 7,7 nhân 1 1 1 1 1 % Các số đặc trưng đo xu thế trung tâm 27, 3 1 1 1 2 1 1 2 4 1 của mẫu số % liệu ghép nhóm Đường thẳng và Quan hệ song 3,8 mặt phẳng 4 song trong trong 1 1 không gian % không gian.. Tổng số câu 8 4 2 4 2 2 2 1 2 10 11 5
Tổng số điểm 2,0 1,0 2,0 1,0 1,0 1,0 2,0 2,5 4,5 3 Tỉ lệ % 30 20 20 30 25 45 30
BẢN ĐẶC TẢ ĐỀ GIỮA HỌC KÌ I – MÔN TOÁN 11 – NĂM HỌC 2025-2026
Số câu hỏi ở các mức độ đánh giá Nội Chương/ dung/đơn TNKQ Tự luận TT
Yêu cầu cần đạt chủ đề vị kiến Nhiều lựa chọn Đúng - Sai Trả lời ngắn thức
Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Nhận biết:
– Nhận biết được các khái
niệm cơ bản về góc lượng
giác: khái niệm góc lượng
giác; số đo của góc lượng
giác; hệ thức Chasles cho
các góc lượng giác; đường tròn lượng giác. Hàm số
– Nhận biết được khái lượng
1.1. Giá trị niệm giá trị lượng giác của giác và
lượng giác một góc lượng giác. 1 phương của một 1 1 1 trình
góc lượng Thông hiểu: lượng giác
– Mô tả được bảng giá trị giác
lượng giác của một số góc
lượng giác thường gặp; hệ
thức cơ bản giữa các giá trị
lượng giác của một góc
lượng giác; quan hệ giữa
các giá trị lượng giác của
các góc lượng giác có liên quan đặc biệt: bù nhau, phụ nhau, đối nhau, hơn kém nhau π.
– Mô tả được các phép
biến đổi lượng giác cơ
bản: công thức cộng; công
thức góc nhân đôi; công
thức biến đổi tích thành
tổng và công thức biến đổi tổng thành tích. Vận dụng:
– Giải quyết được một
số vấn đề thực tiễn gắn
với hàm số lượng giác
(ví dụ: một số bài toán có liên quan đến dao
động điều hoà trong Vật lí,...). Nhận biết:
– Nhận biết được các công
thức lượng giác đã học Thông hiểu: 1.2. Công
thức lượng – Mô tả được các phép 1 1 giác
biến đổi lượng giác cơ bản: công thức cộng;
công thức góc nhân đôi;
công thức biến đổi tích
thành tổng và công thức
biến đổi tổng thành tích. Nhận biết:
– Nhận biết được các khái
niệm về hàm số chẵn, hàm 1.3. Hàm
số lẻ, hàm số tuần hoàn. số lượng 1 giác
– Nhận biết được các đặc
trưng hình học của đồ thị
hàm số chẵn, hàm số lẻ, hàm số tuần hoàn. Nhận biết:
– Nhận biết được công
thức nghiệm của phương
trình lượng giác cơ bản: 1.4.
sin x = m; cos x = m; tan x Phương
= m; cot x = m bằng cách
trình lượng vận dụng đồ thị hàm số 1 1 1
giác cơ bản lượng giác tương ứng. Thông hiểu:
Giải được phương trình lượng giác ở dạng cơ bản Nhận biết:
– Nhận biết được dãy số
hữu hạn, dãy số vô hạn. 2.Dãy số.
– Nhận biết được tính chất Cấp số cộng.
2.1. Dãy số tăng, giảm, bị chặn của 1 2 Cấp số
dãy số trong những trường nhân hợp đơn giản. Nhận biết:
– Nhận biết được một dãy số là cấp số cộng. Thông hiểu:
– Giải thích được công
2.2. Cấp số thức xác định số hạng tổng cộng
quát của cấp số cộng. 1 1 2 1 1 Vận dụng:
– Tính được tổng của n số
hạng đầu tiên của cấp số cộng. Thông hiểu:
– Giải thích được công
thức xác định số hạng tổng quát của cấp số nhân. Vận dụng:
– Tính được tổng của n số
2.3. Cấp số hạng đầu tiên của cấp số nhân nhân. 1 1 1
– Giải quyết được một số
vấn đề thực tiễn gắn với
cấp số nhân để giải một
số bài toán liên quan đến
thực tiễn (ví dụ: một số vấn đề trong Sinh học,
trong Giáo dục dân số,...). Nhận biết:
– Nhận biết được mối liên hệ
giữa thống kê với những
3.1. Mẫu kiến thức của các môn học số liệu
khác trong Chương trình lớp
ghép nhóm 11 và trong thực tiễn Thông hiểu:
– Hiểu được cách lập mẫu số liệu ghép nhóm Nhận biết:
– Nhận biết được mối liên hệ 3. Các số
giữa thống kê với những đặc trưng đo
kiến thức của các môn học xu thế
khác trong Chương trình lớp trung 11 và trong thực tiễn . 3 tâm của Thông hiểu: mẫu số
– Hiểu được ý nghĩa và vai liệu ghép
trò của các số đặc trưng nói nhóm
3.2. Các số trên của mẫu số liệu trong đặc trưng thực tiễn
của mẫu số Vận dụng: 1 1 1 2 1 1 liệu ghép nhóm
- Tính được các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm: số trung bình cộng (hay số trung
bình), trung vị (median),
tứ phân vị (quartiles), mốt (mode). 4.1. Đường thẳng và
4.Đường mặt phẳng – Nhận biết được các thẳng và trong quan hệ liên thuộc cơ mặt không
bản giữa điểm, đường 4 phẳng gian.
thẳng, mặt phẳng trong 1 trong Cách xác không
định mặt không gian. gian phẳng. Hình chóp và hình tứ diện Tổng số câu 8 4 2 4 2 2 2 1 2 Tổng số điểm 2,0 1,0 2,0 1,0 1,0 1,0 2,0 Tỉ lệ % 30 20 20 30
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 11
https://toanmath.com/de-thi-giua-hk1-toan-11





