Đề giữa học kỳ 1 Toán 9 năm 2025 – 2026 trường THCS Nguyễn Gia Thiều – TP HCM

UBND PHƯỜNG PHƯỚC THẮNG
TRƯỜNG THCS NGUYỄN GIA THIỀU
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 NĂM HỌC 2025- 2026 MÔN TOÁN 9
Mức độ đánh giá Tổng % (4-11) điểm (12) TT Chương/
Nội dung/ Đơn vị kiến (1) Chủ đề thức
Nhận biết Thông hiểu Vận dụng (2) (3) TN TN KQ TL K TL TN Q KQ TL Phương trình quy về 1 1
phương trình bậc nhất một 20 Phương ẩn 1đ 1đ
trình và hệ Phương trình bậc nhất hai 1 1
phương ẩn và hệ phương trình bậc 10 trình nhất hai ẩn 1đ
Giải bài toán bằng cách lập 1
phương trình, hệ phương 10 trình 1đ Bất 1 1
phương Bất đẳng thức 10 0,5 đ 0,5 đ 2 trình bậc
nhất một Bất phương trình bậc nhất 1 10 ẩn một ẩn 1đ
Toán thực tế về tỉ số lượng
giác của góc nhọn. Một số 1 10
hệ thức giữa cạnh và góc 1 đ
Hệ thức trong tam giác vuông lượng 3 Vẽ trong tam
giác vuông Tỉ số lượng giác của góc hình 2
nhọn. Một số hệ thức giữa 0,5 đ 30
cạnh và góc trong tam giác 1,5đ vuông; hình học phẳng 1 1đ Tổng câu 2 6 2 12 Tổng điểm 1,5 5,5 3,0 10 Tỉ lệ % 15% 55% 30% 100% Tỉ lệ chung 70% 30% 100%
BẢN ĐẶC TẢ MỨC ĐỘ ĐÁNH GIÁ GIỮA HỌC KÌ I MÔN TOÁN – LỚP 9 Nội dung/
Số câu hỏi theo mức độ TT Chương/ nhận thức
Chủ đề Đơn vị kiến
Mức độ đánh giá thức Nhận Thông Vận biết hiểu dụng Phương
Nhận biết: Biết cách giải phương trình
trình quy về tích dạng cơ bản phương
Thông hiểu: Giải được phương trình tích, B1a B1b trình bậc
phương trình chứa ẩn ở mẫu đưa về 1,0đ 1,0đ
nhất một ẩn phương trình bậc nhất. Phương Phương
trình và trình và hệ Thông hiểu: Biết giải hệ phương trình cơ 1 hệ hai phương phương trình bậc bản B1c 1,0đ trình nhất hai ẩn Giải bài toán bằng cách
lập phương Vận dụng: Vận dụng để giải bài toán trình, hệ
thực tế bằng cách lập hệ phương trình. B3 1,0đ phương trình
Nhận biết:Nhận biết được tính chất bất B2a đẳng thức 0,5đ Bất Bất đẳng phương thức
Vận dụng cao:Vận dụng được tính chất 2 trình bậc
bất đẳng thức chứng minh đẳng thức ở bài B6 0,5đ nhất một toán thực tế ẩn Bất phương trình bậc
Thông hiểu: Giải được bất phương trình
nhất một ẩn bậc nhất một ẩn B2b 1,0đ Toán thực tế về tỉ số
Thông hiểu: Biết tính chiều cao của một lượng giác
vật theo hệ thức giữa cạnh và góc trong B4 của góc tam giác vuông. 1,0đ nhọn Hệ thức Vẽ hình lượng
Thông hiểu: Vẽ được hình, tính được độ
Tỉ số lượng dài cạnh, số đo góc (0,5) 3 trong B5a
tam giác giác của góc 1,0đ vuông nhọn. Một
Vận dụng: Dựa vào tỉ số lượng giác, tìm số hệ thức B5b
giữa cạnh và số đo 1 góc 1,0đ góc trong
- Giải được tam giác vuông, tính độ dài tam giác cạnh, số đo góc .. vuông Vận dụng cao B5c
- Áp dụng hệ thức lượng, tỉ số lượng giác 0,5đ
của góc nhọn chứng minh các đẳng thức… Tổng 2 6 4 Tổng điểm(%) 1,5đ 5,5đ 3đ 15% 55% 30% Tỉ lệ chung 7,0đ 3,0đ 70% 30%
UBND PHƯỜNG PHƯỚC THẮNG
ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ I
TRƯỜNG THCS NGUYỄN GIA THIỀU
NĂM HỌC 2025 – 2026 MÔN: TOÁN 9 Mã đề 001 THỜI GIAN: 90 phút
(Không kể thời gian phát đề) ĐỀ BÀI:
Bài 1: (3,0 điểm) Giải các phương trình, hệ phương trình sau: x − 2y = 11 a) ( 1 2 3
x +3)(2x −5)= 0 b) + = c) 2 x − 2 x + 2 x − 4  5x + 3y = 3
Bài 2: (1,5 điểm) a) Cho a > b , chứng tỏ rằng 4a + 5 > 4b + 5
b) Giải bất phương trình sau: x + 5 ≤ 3x −9
Bài 3: (1,0 điểm) Trong kỳ thi tốt nghiệp THPT môn toán lớp 9, một phòng thi của trường
có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát cho, cuối
buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 59 tờ giấy thi. Hỏi trong
phòng thi có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy
thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.
Bài 4: (1,0 điểm) Ca nô dù bay là một trò chơi
thể thao biển được ưa chuộng, trong đó người
chơi được đeo dù và được ca nô kéo bay lên để
thưởng ngoạn cảnh biển từ trên cao như Hình
vẽ. Nếu biết độ dài AC của dây kéo là 160 (m)
và góc ACB tạo bởi dây và phương ngang là
250, làm thế nào để tính được độ cao AB của
người chơi so với mặt biển? (làm tròn kết quả đến hàng phần mười).
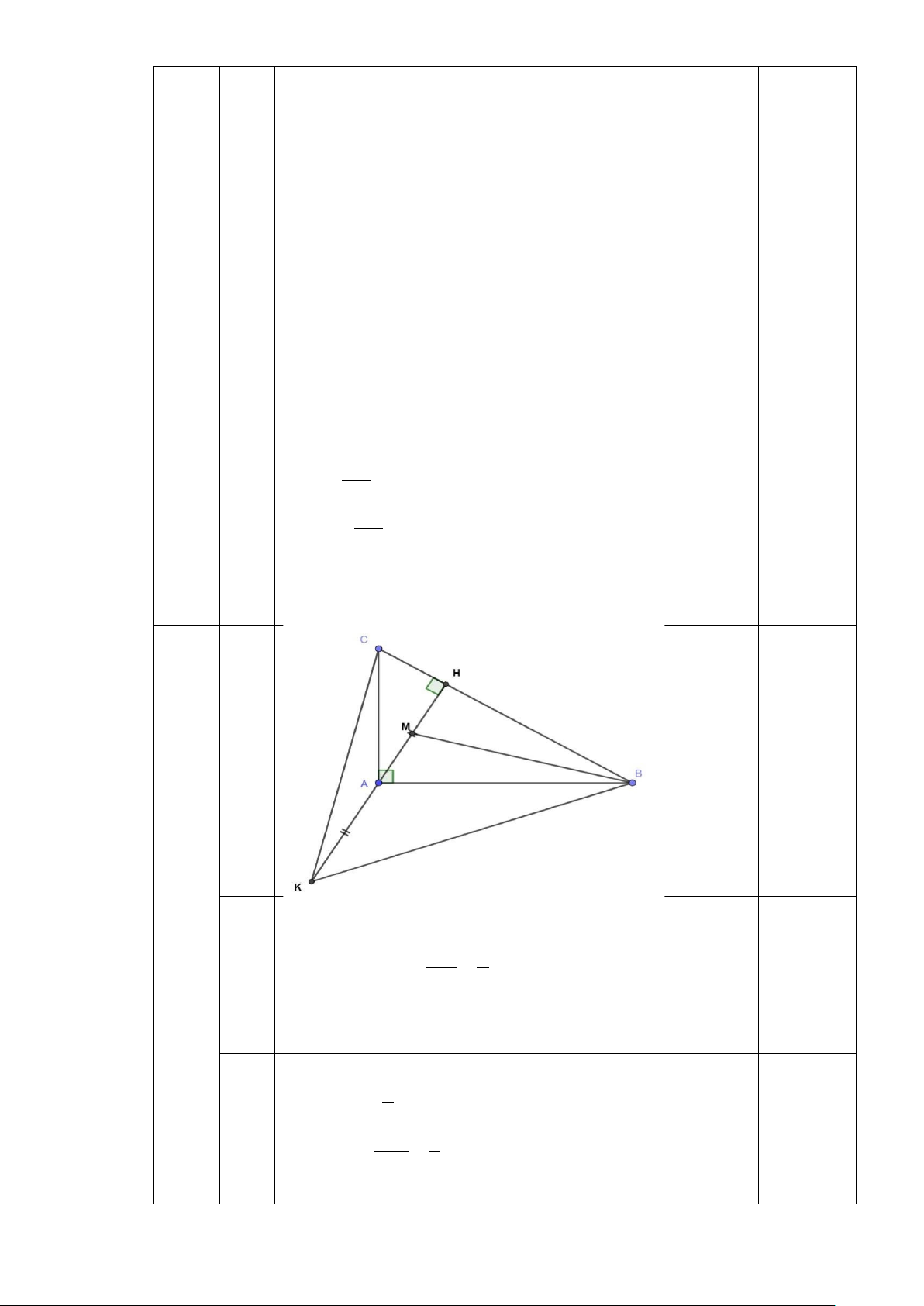
Bài 5: (3,0 điểm) Cho tam giác ABC vuông tại A (AB < AC), có AH là đường cao.
Biết AB = 6cm và BH = 3,6 cm.
a) Tính độ dài AH và số đo góc ABH (làm tròn số đo góc đến độ).
b) Gọi M là trung điểm AH. Tính số đo góc MBH (kết quả làm tròn đến độ).
c) Trên tia HA lấy điểm K sao cho A là trung điểm HK. Chứng minh HK.HM =  
sin BKH.sinCKH (Học sinh không dùng số liệu để chứng minh câu c). . KB KC
Bài 6: (0,5 điểm) Một rạp chiếu phim có 120 ghế, giá vé hiện tại là 100 nghìn đồng mỗi vé.
Với giá vé này, tất cả các ghế đều được bán hết cho mỗi suất chiếu. Ban quản lý rạp phim
đang xem xét việc tăng giá vé để tối ưu hóa doanh thu. Sau khi thử nghiệm, rạp phim nhận
thấy cứ mỗi lần tăng giá thêm 5 nghìn đồng, số ghế bị bỏ trống sẽ tăng thêm 4 ghế. Hỏi mức
giá vé mới là bao nhiêu để rạp phim đạt doanh thu lớn nhất?
-------------------------Hết-------------------------
UBND PHƯỜNG PHƯỚC THẮNG
ĐÁP ÁN ĐỀ KIỂM TRA GIỮA KÌ I
TRƯỜNG THCS NGUYỄN GIA THIỀU MÔN TOÁN LỚP 9
NĂM HỌC 2025 – 2026 Bài Ý Đáp án Điểm a
(x +3)(2x −5)= 0 TH1: x + 3 = 0
TH2 : 2x − 5 = 0 0,5 5 x = −3 x = 0,25x2 2 1 2 3 + = ĐKXĐ: x ≠ 2 ± 2 x − 2 x + 2 x − 4 0,25 x + 2 + 2(x − 2) = 3 0,25
x + 2 + 2x − 4 = 3 b 3x − 5 = 0 0,25 3x = 5 5 x = 0,25 1 3 (3,0)
Vậy phương trình có nghiệm 5 x = 3 c x − 2y = 11 0,25x4  5x + 3y = 3 5  x −10y = 55 5   x + 3y = 3  13 − y = 52  x − 2y = 11 y = 4 −  x − 2y = 11 x = 3  y = 4 − a a > b 4a > 4b 0,25
4a + 5 > 4b + 5 0,25 2 b
x + 5 ≤ 3x − 9 x − 3x ≤ 9 − − 5 0,5 2 − x ≤ 14 − 0,25 0,25 x ≤ 7 a
Gọi số học sinh làm bài 2 tờ giấy thi là x (x ∈ ℕ*) (học 0,25 sinh) 3
Số học sinh làm bài 3 tờ giấy thi là y (y ∈ ℕ*) (học sinh)
Vì có 24 thí sinh dự thi mà có 3 thí sinh làm 1 tờ giấy thi nên ta có phương trình: x + y + 3 = 24 0,25 x + y = 21 (1)
Vì tổng số tờ giấy thi là 59 tờ và có 3 thí sinh làm 1 tờ giấy
thi nên ta có phương trình: 2x + 3y + 3 = 59 0,25 2x + 3y = 56 (2) x − 2y = 11
Từ (1) và (2), ta có hệ phương trình:  5x + 3y = 3
Giải hệ phương trình ta được x = 7 và y =14 0,25
Vậy có 7 thí sinh làm bài 2 tờ giấy thi và có 14 thí sinh làm 3 tờ giấy thi. 4
Gọi chiều cao của người chơi cách mặt biển là AB. 0,25
Xét tam giác ABC vuông tại B, ta có: sin = AB C 0,25 AC 0 sin 25 = AB 160 AB ≈ 67,6m 0,25
Vậy chiều cao của người chơi cách mặt biển khoảng 67,6m. 0,25 Vẽ hình đến câu a 0,5 5 a
Xét tam giác ABH vuông tại H 0,25 Tính được AH = 4,8cm 0,25 Ta có: AH 4 sin ABH = = AB 5 0,25  0,25 0 ABH = 53 b Vì M là trung điểm AH 1 MA 0,25
= MH = AH = 2,4cm 2 0,25  HM 2 0,25 tan MBH = = HB 3 0,25  0 MBH = 34 c   sin .sin = HK . HC BKH CKH 0,25 KB KC 2 . = HB HC = HA . KB KC . KB KC 0,25 1 2 . HA HA 2 HK. = = HM . KB KC . KB KC 6
Gọi số lần tăng giá là x (lần) ( * x ∈ N )
Giá tiền 1 vé sau x lần tăng là (100 + 5x) (nghìn đồng)
Số ghế đã bán sau x lần tăng giá là 120 – 4x (ghế) 0,25
Tổng số tiền thu được: A = (100 + 5x)(120 − 4x) (nghìn đồng)
Để có doanh thu lớn nhất thì A đạt giá trị lớn nhất 2 A = 20
− x + 200x +12000 2 2 = 20( −
x −10x + 5 ) +12500 = 20 − (x −5)2 +12500 Ta có : 20x  52  0
20x  52 12500  12500 A  12500 0,25
A đạt giá trị lớn nhất khi x = 5.
Vậy mức giá mới cho một vé là 100  25  125 (nghìn
đồng) thì rạp phim sẽ đạt doanh thu lớn nhất.
Lưu ý: HS có cách giải khác, đúng vẫn cho điểm theo bước.
UBND PHƯỜNG PHƯỚC THẮNG
TRƯỜNG THCS NGUYỄN GIA THIỀU
KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ I MÔN TOÁN – LỚP 9
Mức độ đánh giá Tổng % T (4-11) điểm T Chương/
Nội dung/ Đơn vị kiến (12) (1 Chủ đề thức Nhận biết Thông hiểu Vận dụng ) (2) (3) TNKQ TL TNKQ TL TN KQ TL Giải phương trình tích,
phương trình chứa ẩn ở 1 1 20
Phương mẫu đưa về pt bậc nhất 1 (1,0 đ) (1,0 đ) trình và hệ ẩn 1 phương 1 10 trình Giải hệ phương trình (1,0 đ)
Giải bài toán bằng cách lập 1
phương trình, hệ phương 10 trình (1,0 đ) 1 1
Bất phương Bất đẳng thức 10 (0,5 đ) (0,5 đ) 2 trình bậc
nhất một ẩn Giải bất phương trình bậc 1 10 nhất một ẩn (1,0 đ)
Toán thực tế về tỉ số lượng
giác của góc nhọn. Một số 1 10
hệ thức giữa cạnh và góc (1.0 đ)
Hệ thức trong tam giác vuông lượng trong 3 Vẽ tam giác vuông
Tỉ số lượng giác của góc hình 2
nhọn. Một số hệ thức giữa (0,5 đ) 30
cạnh và góc trong tam giác (1,5 đ) vuông; hình học phẳng 1 (1,0 đ) Tổng câu 2 6 4 Tổng điểm 1,5 5,5 3,0 Tỉ lệ % 15% 55% 20% 100 Tỉ lệ chung 70% 30% 100
UBND PHƯỜNG PHƯỚC THẮNG
TRƯỜNG THCS NGUYỄN GIA THIỀU
BẢN ĐẶC TẢ MỨC ĐỘ ĐÁNH GIÁ GIỮA HỌC KÌ I MÔN TOÁN – LỚP 9 Nội dung/
Số câu hỏi theo mức độ nhận thức TT Chương/
Chủ đề Đơn vị kiến
Mức độ đánh giá thức
Nhận biết Thông hiểu Vận dụng Phương
trình quy về - Nhận biết: giải được phương trình tích.
phương trình - Thông hiểu: Giải phương trình chứa ẩn ở Bài 1a Bài 1b
bậc nhất một mẫu đưa về phương trình bậc nhất. Phương ẩn trình và Phương 1 hệ
trình và hệ Thông hiểu:
phương hai phương – Giải được hệ phương trình bậc nhất hai Bài 1c trình trình bậc ẩn. nhất hai ẩn Cách giải hệ
hai phương Vận dụng: Vận dụng để giải hệ hai trình
bậc phương trình bậc nhất hai ẩn bằng phương Bài 4
nhất hai ẩn pháp thế, cộng đại số Nhận biết: Bất Bất
đẳng - Nhận biết được tính chất bất đẳng thức Bài 2a phương thức Vận dụng cao 2 trình bậc
- Vận dụng được tính chất bất đẳng thức Bài 6 nhất một
giải quyết bài toán thực tiễn ẩn
Bất phương Thông hiểu: trình
bậc - Giải được bất phương trình bậc nhất một Bài 2b nhất một ẩn ẩn
Tỉ số lượng Thông hiểu:
giác của góc - Biết tính chiều cao của một vật theo hệ
thức giữa cạnh và góc trong tam giác Bài 3 Hệ thức nhọn vuông. lượng
Thông hiểu: Giải tam giác vuông 3 trong Vẽ hình (0,5) Bài 5a
tam giác Một số hệ Vận dụng: vuông thức
giữa - Áp dụng các tính chất, hệ thức chứng Bài 5b cạnh và góc trong tam minh đẳng thức
giác vuông Vận dụng cao
- Áp dụng hệ thức lượng, tỉ số lượng giác Bài 5c
của góc nhọn chứng minh các đẳng thức… Tổng 2 6 4 Tỉ lệ % 15 55 30 Tỉ lệ chung 70 30
UBND PHƯỜNG PHƯỚC THẮNG
ĐỀ KIỂM TRA GIỮA KÌ I
TRƯỜNG THCS NGUYỄN GIA THIỀU MÔN TOÁN LỚP 9
NĂM HỌC 2025 – 2026 Mã đề 002
Thời gian làm bài: 90 phút ĐỀ BÀI:
Bài 1: (3,0 điểm) Giải các phương trình, hệ phương trình sau: a) (  x + y = 2x − + ) 1 (x −3) = 0 b) 1 4 3x 3 − = c) 3 3 2
x − 3 x + 3 x − 9  2x − y = 7
Bài 2: (1,5 điểm) a) Cho a > b , chứng tỏ rằng 2 + 5a > 2 + 5b
b) Giải bất phương trình sau: 5(x −3) + 6 > 6(x − ) 1
Bài 3: (1,0 điểm) Cho hình vẽ, tính
chiều cao của tháp canh trong hình
(kết quả làm tròn đến chữ số thập phân thứ hai)
Bài 4: (1,0 điểm) Một ô tô và một xe máy ở hai điểm A và B cách nhau 180km, khởi hành
cùng một lúc đi ngược chiều nhau và gặp nhau sau 2 giờ. Biết vận tốc của ô tô lớn hơn vận
tốc của xe máy là 10km/h. Tính vận tốc của ô tô và xe máy.
Bài 5: (3,0 điểm) Cho tam giác ABC vuông tại A, đường cao AH (H ∈ BC).
a) Biết AB = 6cm, AC = 8cm. Giải tam giác ABC (góc làm tròn đến phút).
b) Chứng minh rằng: BH. BC = AB2
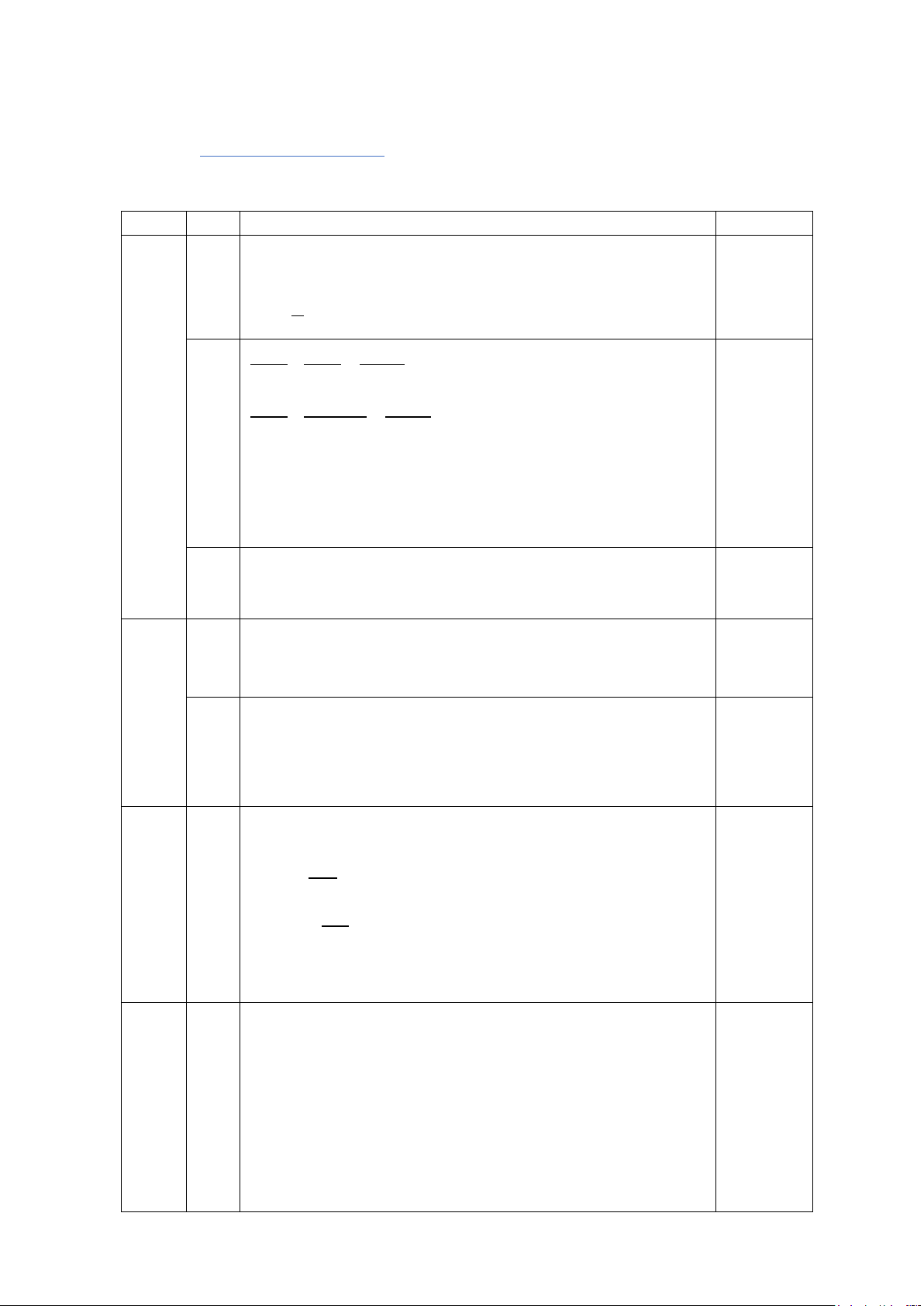
c) Trên cạnh AC lấy điểm D. Vẽ AK vuông góc với BD tại K. Chứng minh  =  BAH BKH
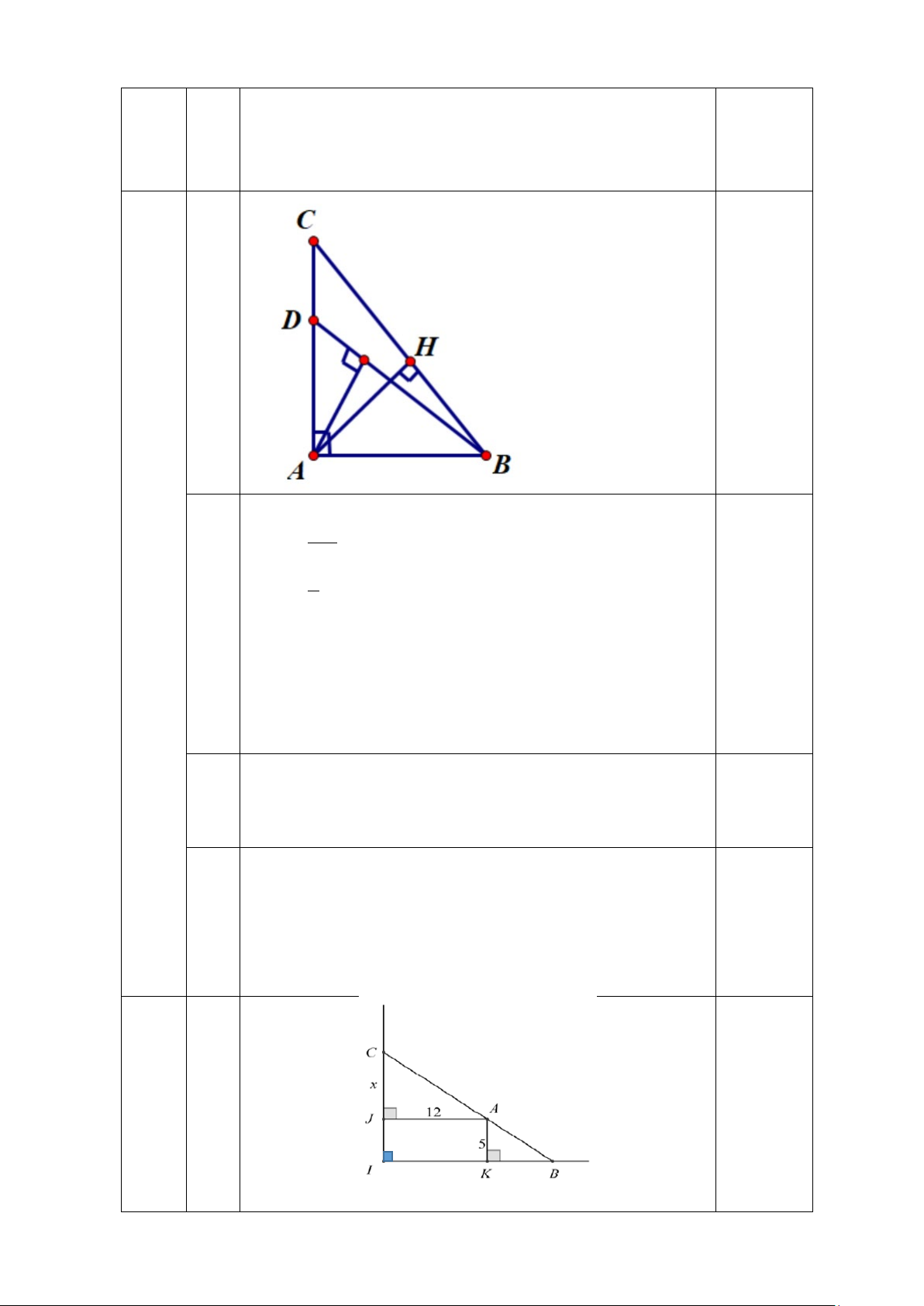
Bài 6: (0,5 điểm) Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng
lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc
và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Hỏi diện tích nhỏ nhất có thể giăng là bao
nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
-------------------------Hết-------------------------
Họ và tên thí sinh:…………………………………..……………..SBD………………………
Chữ kí của giám thị…………………………………………………………………………….
UBND PHƯỜNG PHƯỚC THẮNG
ĐÁP ÁN ĐỀ KIỂM TRA GIỮA KÌ I
TRƯỜNG THCS NGUYỄN GIA THIỀU MÔN TOÁN LỚP 9
NĂM HỌC 2025 – 2026 Bài Ý Đáp án Điểm a
(2x + )1(x −3) = 0
2x +1 = 0 hoặc x − 3 = 0 1 0,5
x = − hoặc x = 3 2 0,25x2 1 4 3x − 3 − = ĐKXĐ: x ≠ 3 ± 0,25 2
x − 3 x + 3 x − 9 x + 3 4(x − 3) 1 3x − 3 − = 2 (3,0) x − 3 x + 3 x − 9 b
x + 3− 4x +12 = 3x − 3 0,25 6 − x +18 = 0 0,25 x = 3(l) 0,25
Vậy phương trình vô nghiệm c
3x + y = 3  5x =10  x = 2  x = 2 0,5 
2x y 7 2x y 7  0,25x2 2.2 y 7  − = − = − = y = 3 − a a > b 5a > 5b 0,25
2 + 5a > 2 + 5b 0,25 2 b
5(x −3) + 6 > 6(x − ) 1
5x −15 + 6 > 6x − 6 0,5 0,25 −x > 3 0,25 x < 3 − 3
Gọi chiều cao của tháp canh là AB. 0,25
Xét tam giác ABC vuông tại B, ta có: tan AB C = 0,25 BC 0 tan 60 AB = 5,8 AB ≈10,05m 0,25
Vậy chiều cao của tháp canh khoảng 10,05m 0,25
Gọi vận tốc của ô tô và xe máy lần lượt là x và y (km/h, 0,25 x, y>0)
Quãng đường đi được của ô tô sau 2h là 2x (km) 0,25
Quãng đường đi được của xe máy sau 2h là 2y (km) 4 Theo bài ta có hpt: 2x + 2y =180 0,25   x − y =10 0,25
Giải hpt ta được: x = 50  y = 40
Vậy vận tốc của ô tô là 50km/h, vận tốc của xe máy là 40km/h Vẽ hình đến câu a 0,5 a
Xét tam giác ABC vuông tại A, ta có: 0,25 tan AC B = AB 8 5 tan B = 6 0,25  0 ' B ≈ 53 8 =>  0,25 0 0 ' 0 '
C = 90 − 53 8 = 36 52 2 2 2
BC = AB + AC 2 2 2 BC = 6 + 8 =100 BC =10 0,25 b
Chứng minh được: tam giác ABH đồng dạng tam giác 0,25x3 CBA Suy ra BH. BC = AB2 0,25 c
Chứng minh được: BK. BD = AB2 Suy ra BH. BC = BK. BD 0,25
Chứng minh được tam giác BKH đồng dạng với tam giác BCD Chứng minh  =  BAH BCA Suy ra  =  BAH BKH 0,25 6
Đặt tên các điểm như hình vẽ
Đặt CJ = x,(x > 0).
Chứng minh hai tam giác AJC và BKA là hai tam giác đồng dạng, suy ra: CJ JA x 12 60 = ⇔ = ⇔ KB = . AK KB 5 KB x
Diện tích của khu nuôi cá là: 1 S (x )  60 5 . 12 = + +  . 2  x  1  300 S(x)  60 12x 60 = + + + 2 x    150
S(x) = 6x + + 60 0,25 x 2   Ta có: 150  6x −  ≥ 0  với mọi x > 0 x    Suy ra: 150 150 6x + ≥ 2 6 . x = 60 x x Dấu bằng xảy ra khi 150 2 6 x =
⇔ x = 25 ⇔ x = 5 . x Nên 150
S(x) = 6x + + 60 ≥ 60 + 60 = 120 x
Suy ra diện tích nhỏ nhất có thể giăng là 2 120 m , đạt 0,25
được khi x = 5m.
Lưu ý: HS có cách giải khác, đúng vẫn cho điểm theo bước.
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 9
https://thcs.toanmath.com/de-thi-giua-hk1-toan-9
Document Outline

• TOÁN 9_GK1_MÃ ĐỀ 001
  • Bài 6: (0,5 điểm) Một rạp chiếu phim có 120 ghế, giá vé hiện tại là 100 nghìn đồng mỗi vé. Với giá vé này, tất cả các ghế đều được bán hết cho mỗi suất chiếu. Ban quản lý rạp phim đang xem xét việc tăng giá vé để tối ưu hóa doanh thu. Sau khi thử nghi...
  • -------------------------Hết-------------------------
• TOÁN 9_GK1_MÃ ĐỀ 002
  • Bài 5: (3,0 điểm) Cho tam giácvuông tại , đường cao
  • a) Biết AB = 6cm, AC = 8cm. Giải tam giác ABC (góc làm tròn đến phút).
  • b) Chứng minh rằng: BH. BC = AB2
  • Bài 6: (0,5 điểm) Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Hỏi diện tích nhỏ ...
  • Chữ kí của giám thị…………………………………………………………………………….
• XEM THEM - GIUA KY 1 - TOAN 9