Đề giữa kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Kẻ Sặt – Hải Dương

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra giữa học kỳ 1 môn Toán 10 năm học 2024 – 2025 trường THPT Kẻ Sặt, tỉnh Hải Dương. Đề thi có đáp án chi tiết và hướng dẫn chấm điểm mã đề 101 – 102.Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

4 2 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 10

Môn: Toán 10

Thông tin:

11 trang 1 ngày trước

Tác giả:

Profile Lê Phương
1
SỞ GD&ĐT HẢI DƯƠNG
TRƯỜNG THPT KẺ SẶT
ĐỀ CHÍNH THỨC
( Đề thi có04 .trang)
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
NĂM HỌC 2024 - 2025
MÔN:TOÁN KHỐI 10
Thời gian làm bài:90 phút không kể thời gian phát đề
Họ và tên học sinh:……………………….Lớp:……Số báo danh………..
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 16
Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1. Mệnh đề là:
A. Câu cảm thán B. Một khẳng định chỉ có thể đúng hoặc sai
C. Một khẳng định luôn đúng D. Câu nghi vấn hoặc câu cầu khiến
Câu 2. Câu nào trong các câu sau không phải là mệnh đề?
A.
π
có phải là một số vô tỷ không? B.
225+=
.
C.
2
là một số hữu tỷ. D.
4
2
2
=
.
Câu 3. Phủ định của mệnh đề: “
2
:1
nn∀∈ +
không chia hết cho 3” là:
A. “
2
:1nn∀∈ +
chia hết cho 3” B. “
2
:1nn∃∈ +
không chia hết cho 3”.
C. “
2
:1nn∃∈ +
chia hết cho 3”. D. “
không chia hết cho 3”.
Câu 4. Mệnh đề nào sau đây sai ?
A. Tam giác ABC đều
AB AC⇔=
và
0
A 60=
.
B.
63nn⇔
và
2n
.
C.
ABCD
là hình chữ nhật
AC BD
⇔=
.
D.
2
3 3,n n nN
⇔ ∀∈
.
Câu 5. Giá trị của
oo
cos60 sin 30+
bằng bao nhiêu?
A.
3
2
B.
3
C.
3
3
D.
1
Câu 6.Trong các đẳng thức sau, đẳng thức nào đúng?
A.
( )
o
sin 180 cos
αα
−=−
. B.
( )
o
sin 180 sin
αα
−=−
.
C.
( )
o
sin 180 sin
αα
−=
. D.
(
)
o
sin 180 cos
αα
−=
.
Câu 7. Cho
1
cos
2
x =
. Tính biểu thức
22
3sin 4cosPxx= +
A.
13
4
. B.
7
4
. C.
11
4
. D.
15
4
.
Câu 8. Hãy liệt kê các phần tử của tập hợp
{ }
sao cho 8M xN x= ∈ lµ íc cña
.
A.
{ }
1; 4;16;64M =
. B.
{ }
0;1; 4;16; 64M =
.
Mã đề:101
2
C.
{ }
1; 2; 4;8M =
. D.
{ }
0;1; 2; 4;8M =
.
Câu 9. Trong các tập hợp sau, tập hợp nào là tập rỗng?
A.
{ }
2
5 60∈ + −=
x xx
. B.
{ }
2
3 5 20∈ − +=x xx
.
C.
{ }
2
10∈ + −=
x xx
. D.
{ }
2
5 10∈ + −=x xx
.
Câu 10. Cho
[ ]
( 2;1), 3; 5AB=−=−
. Khi đó
AB∩
là tập hợp nào sau đây?
A.
( 2;1)−
. B.
[ ]
2;5−
. C.
[ ]
2;1−
. D.
(
]
2;5−
.
Câu 11. Cho tập
X
có biểu diễn trên trục số như hình sau:
Khẳng định nào sau đây đúng.
A.
X
là khoảng,
( )
5;X = − +∞
. B.
X
là khoảng,
( )
;5X = −∞ −
.
C.
X
là nửa khoảng,
(
]
;5X
= −∞ −
. D.
X
là nửa khoảng,
(
]
;5
X = −∞ −
.
Câu 12. Cho tập hợp
[ ]
3; 5
A = −
. Viết lại tập hợp
A
bằng cách chỉ ra tính chất đặc trưng.
A.
{ }
35
Ax x∈−
= ≤≤
. B.
{ }
35Ax x∈−= <<
.
C.
{ }
35Ax x∈−= ≤≤
. D.
{ }
35Ax x∈−= ≤≤
.
Câu 13. Cặp số
( )
1; –1
là nghiệm của bất phương trình nào sau đây?
A.
–3 0xy+>
. B.
–– 0xy<
.
C.
3 10xy+ +<
. D.
.
Câu 14. Miền nghiệm của bất phương trình
32 6
xy− <−
là
A.
B.
O
x
y
2−
3
O
2
3
y
x
3
C.
D.
Câu 15. Miền nghiệm của hệ bất phương trình
≤
−≥
−
≥
≥
+
6
82
3
9
3
y
xy
y
x
yx
là phần mặt phẳng chứa điểm nào
sau đây?
A.
( )
0;0
. B.
( )
1; 2
. C.
( )
2;1
. D.
( )
8; 4
.
Câu 16.Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình
nào trong bốn hệ A, B, C, D?
A.
0
32 6
y
xy
>
+<
. B.
0
32 6
y
xy
>
+ <−
.
C.
0
32 6
x
xy
>
+<
. D.
0
32 6
x
xy
>
+ >−
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1.Cho tam giác
ABC
có
ˆ
7 , 5 , 120
°
= = =b cm c cm A
. Khi đó:
a)
127 a cm=
c)
cos 0,21B ≈
b)
cos 0,91C ≈
d)
6, 03( )R cm≈
Câu 2. Cho các tập hợp
{0;1; 2; 3; 4}; {0;1; 2}; { 3; 0;1; 2}= = = −A BC
. Khi đó:
a)
\ {3; 4}AB=
c)
( \ ) { 3; 0;1; 4}A CB∪=−
b)
( )\ACB∩=∅
d)
{1; 3; 4}
A
CB=
O
2
3
y
x
O
x
2
−
3
y
O
x
y
2
−
3
4
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2
Câu 1: Bạn An kinh doanh hai mặt hàng hanhmade là vòng tay và vòng đeo cổ. Mỗi vòng tay
làm trong 4 giờ, bán được 40 000 đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 000. Mỗi
tuần bạn an bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong một
tuần An cần dùng để bán được ít nhất 400 000 đồng.
Câu 2. Cho hai tập hợp
(
] [
]
; 3 4;A
= −∞ − ∪ +∞
và
[
)
1; 2 ,m m mZ−+ ∈
. Tìm tổng các giá trị
của m để
AB∩=∅
.
PHẦN IV.Tự luận:
Câu 1:
Cho hai tập hợp
{ }
27
A xR x
= ∈ −< <
và
( ;5)B
= −∞
. Tìm các tập hợp
,.ABAB∩∪
Câu 2:Cho góc
α
thỏa mãn
tan 2
α
=
. Tính giá trị của biểu thức
2
22
3sin 2cos .sin 1
3cos 4sin
P
α αα
αα
−+
=
−
.
Câu 3: Từ vị trí
A
người ta quan sát một cây cao (hình vẽ). Biết
4AH m=
,
20HB m=
,
45BAC
= °
. Tính chiều cao của cây ( kết quả làm tròn đến chữ số hàng phần trăm).
------------Hết----------
- Thí sinh không được sử dụng tài liệu;
- Giám thị không giải thích gì thêm.
1
SỞ GD&ĐT HẢI DƯƠNG
TRƯỜNG THPT KẺ SẶT
ĐỀ CHÍNH THỨC
( Đề thi có04 .trang)
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
NĂM HỌC 2024 - 2025
MÔN:TOÁN KHỐI 10
Thời gian làm bài:90 phút không kể thời gian phát đề
Họ và tên học sinh:……………………….Lớp:……Số báo danh………..
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 16
Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1.Trong các đẳng thức sau, đẳng thức nào đúng?
A.
( )
o
sin 180 cos
αα
−=−
. B.
( )
o
sin 180 sin
αα
−=−
.
C.
( )
o
sin 180 sin
αα
−=
. D.
( )
o
sin 180 cos
αα
−=
.
Câu 2. Cho
1
cos
2
x
=
. Tính biểu thức
22
3sin 4 cosPxx= +
A.
13
4
. B.
7
4
. C.
11
4
. D.
15
4
.
Câu 3. Hãy liệt kê các phần tử của tập hợp
{ }
sao cho 8M xN x= ∈ lµ íc cña
.
A.
{ }
1; 4;16;64M =
. B.
{ }
0;1; 4;16; 64M =
.
C.
{ }
1; 2; 4;8M =
. D.
{ }
0;1; 2; 4;8M =
.
Câu 4. Trong các tập hợp sau, tập hợp nào là tập rỗng?
A.
{ }
2
5 60∈ + −=x xx
. B.
{
}
2
3 5 20
∈ − +=
x xx
.
C.
{ }
2
10∈ + −=
x xx
. D.
{ }
2
5 10
∈ + −=
x xx
.
Câu 5. Cho
[ ]
( 2;1), 3; 5AB
=−=−
. Khi đó
AB∩
là tập hợp nào sau đây?
A.
( 2;1)−
. B.
[ ]
2;5−
. C.
[ ]
2;1−
. D.
(
]
2;5−
.
Câu 6. Mệnh đề là:
A. Câu cảm thán B. Một khẳng định chỉ có thể đúng hoặc sai
C. Một khẳng định luôn đúng D. Câu nghi vấn hoặc câu cầu khiến
Câu 7. Câu nào trong các câu sau không phải là mệnh đề?
A.
π
có phải là một số vô tỷ không? B.
225+=
.
C.
2
là một số hữu tỷ. D.
4
2
2
=
.
Câu 8. Phủ định của mệnh đề: “
2
:1nn∀∈ +
không chia hết cho 3” là:
A. “
2
:1nn∀∈ +
chia hết cho 3” B. “
2
:1
nn∃∈ +
không chia hết cho 3”.
C. “
2
:1nn∃∈ +
chia hết cho 3”. D. “
không chia hết cho 3”.
Câu 9. Mệnh đề nào sau đây sai ?
A. Tam giác ABC đều
AB AC⇔=
và
0
A 60=
.
Mã đề:102
2
B.
63nn⇔
và
2n
.
C.
ABCD
là hình chữ nhật
AC BD⇔=
.
D.
2
3 3,
n n nN
⇔ ∀∈
.
Câu 10. Giá trị của
oo
cos60 sin 30+
bằng bao nhiêu?
A.
3
2
B.
3
C.
3
3
D.
1
Câu 11. Cho tập
X
có biểu diễn trên trục số như hình sau:
Khẳng định nào sau đây đúng.
A.
X
là khoảng,
( )
5;X
= − +∞
. B.
X
là khoảng,
( )
;5X
= −∞ −
.
C.
X
là nửa khoảng,
(
]
;5
X = −∞ −
. D.
X
là nửa khoảng,
(
]
;5X
= −∞ −
.
Câu 12. Cho tập hợp
[
]
3; 5A = −
. Viết lại tập hợp
A
bằng cách chỉ ra tính chất đặc trưng.
A.
{
}
35
Ax x
∈−= ≤≤
. B.
{ }
35Ax x∈−= <<
.
C.
{ }
35Ax x∈−= ≤≤
. D.
{ }
35
Ax x∈−= ≤≤
.
Câu 13.Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình
nào trong bốn hệ A, B, C, D?
A.
0
32 6
y
xy
>
+<
. B.
0
32 6
y
xy
>
+ <−
.
C.
0
32 6
x
xy
>
+<
. D.
0
32 6
x
xy
>
+ >−
.
Câu 14. Cặp số
( )
1; –1
là nghiệm của bất phương trình nào sau đây?
A.
–3 0xy+>
. B.
–– 0xy<
.
C.
3 10xy+ +<
. D.
.
Câu 15. Miền nghiệm của bất phương trình
32 6xy− <−
là
O
2
3
y
x
3
A.
B.
C.
D.
Câu 16. Miền nghiệm của hệ bất phương trình
≤
−≥
−≥
≥+
6
82
3
93
y
xy
yx
yx
là phần mặt phẳng chứa điểm nào
sau đây?
A.
( )
0;0
. B.
( )
1; 2
. C.
( )
2;1
. D.
( )
8; 4
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho các tập hợp
{0;1; 2; 3; 4}; {0;1; 2}; { 3; 0;1; 2}= = = −A BC
. Khi đó:
a)
\ {3; 4}
AB=
c)
( \ ) { 3; 0;1; 4}A CB∪=−
b)
( )\ACB∩=∅
d)
{1; 3; 4}
A
CB=
Câu 2.Cho tam giác
ABC
có
ˆ
7 , 5 , 120
°
= = =b cm c cm A
. Khi đó:
a)
127 a cm=
c)
cos 0,21B
≈
b)
cos 0,91C ≈
d)
6, 03( )R cm≈
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2
Câu 1. Cho hai tập hợp
(
] [ ]
; 3 4;A = −∞ − ∪ +∞
và
[
)
1; 2 ,m m mZ−+ ∈
. Tìm tổng các giá trị
của m để
AB∩=∅
.
O
x
2−
3
y
O
x
y
2−
3
O
x
y
2−
3
O
2
3
y
x
4
Câu 2: Bạn An kinh doanh hai mặt hàng hanhmade là vòng tay và vòng đeo cổ. Mỗi vòng tay
làm trong 4 giờ, bán được 40 000 đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 000. Mỗi
tuần bạn an bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong một
tuần An cần dùng để bán được ít nhất 400 000 đồng.
PHẦN IV.Tự luận:
Câu 1:
Cho hai tập hợp
{ }
27
A xR x
= ∈ −< <
và
( ;5)
B = −∞
. Tìm các tập hợp
,.ABAB∩∪
Câu 2,Cho góc
α
thỏa mãn
tan 2
α
=
. Tính giá trị của biểu thức
2
22
3sin 2cos .sin 1
3cos 4sin
P
α αα
αα
−+
=
−
.
Câu 3: Từ vị trí
A
người ta quan sát một cây cao (hình vẽ). Biết
4AH m=
,
20HB m=
,
45BAC
= °
. Tính chiều cao của cây ( kết quả làm tròn đến chữ số hàng phần trăm).
------------Hết----------
- Thí sinh không được sử dụng tài liệu;
- Giám thị không giải thích gì thêm.
ĐA- HD CHẤM
ĐỀ KIỂM TRA GIỮA KỲ I
NĂM HỌC: 2024 - 2025
MÔN: TOÁN - LỚP: 10
Phần
I II
Số câu
16
2
Câu\Mã đề
101
102
1
B
C
2
A A
3
B A
4
C C
5
D A
6
C B
7
A A
8
A B
9
C C
10
A D
11
B B
12
A A
13
C C
14
B C
15
D B
16
C C
1
SSDD DDSS
2
DDSS SSDD
1
32 2
2
2 32
SỞ GD&ĐT HẢI DƯƠNG
TRƯỜNG THPT KẺ SẶT
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 10
https://toanmath.com/de-thi-giua-hk1-toan-10
1
SỞ GD& ĐT HẢI DƯƠNG
TRƯỜNG THPT KẺ SẶT
(Đáp án - Thang điểm có 02 trang)
ĐÁP ÁN – THANG ĐIỂM
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
NĂM HỌC: 2024 - 2025
MÔN: TOÁN - KHỐI 10
MÃ ĐỀ: 101+102
IV. Tự luận (3,0 điểm)
Câu
Ý
Nội dung
Điểm
1
Cho hai tập hợp
{ }
27A xR x= ∈ −< <
và
( ;5)
B
= −∞
. Tìm các tập hợ
p
,.
ABAB∩∪
Ta có
( 2;7)A = −
0,25
( 2;5)
AB∩=−
0,5
( ;7)
AB∪ = −∞
0,25
2
Cho góc
α
thỏa mãn
tan 2
α
=
. Tính giá trị của biểu thức
2
22
3sin 2cos .sin 1
3cos 4sin
P
α αα
αα
−+
=
−
.
Ta có
tan 2
α
=
nên
cos 0
α
≠
.
Chia cả tử và mẫu của
P
cho
2
cos
α
ta được
22
2
3tan 2 tan 1 tan
1
3 4 tan
P
αα α
α
− ++
= = −
−
0.5
0.5
2
3
Áp dụng định lí Pitago ta có
4 26
AB =
Kẻ đường cao AK,
K BC∈
.
45
°
C
K
B
H
A
Trong tam giác ABK có
1
4 cos
26
BK B=⇒=
. Khi đó góc
0
79B ≈
Do đó
0
56C
≈
Áp dụng định lí sin cho tam giác ABC ta có
0
0
.sin 4 26.sin 45
17,4
sin sin sin sin 56
AB BC AB A
BC m
CA C
= ⇔= = ≈
Vậy cây cao gần 17,4m
0,25
0,25
0,25
0,25
GIÁO VIÊN RA ĐỀ
Lê Quang Hòa
BAN GIÁM HIỆU
PHÓ HIỆU TRƯỞNG
Vũ Văn Phước
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


SỞ GD&ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THPT KẺ SẶT NĂM HỌC 2024 - 2025 MÔN:TOÁN KHỐI 10 ĐỀ CHÍNH THỨC
Thời gian làm bài:90 phút không kể thời gian phát đề
( Đề thi có04 .trang)
Họ và tên học sinh:……………………….Lớp:……Số báo danh……….. Mã đề:101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 16
Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1. Mệnh đề là:
A. Câu cảm thán B. Một khẳng định chỉ có thể đúng hoặc sai
C. Một khẳng định luôn đúng D. Câu nghi vấn hoặc câu cầu khiến
Câu 2. Câu nào trong các câu sau không phải là mệnh đề?
A. π có phải là một số vô tỷ không? B. 2 + 2 = 5 .
C. 2 là một số hữu tỷ. D. 4 = 2 . 2
Câu 3. Phủ định của mệnh đề: “ 2 n
∀ ∈  : n +1 không chia hết cho 3” là: A. “ 2 n
∀ ∈  : n +1 chia hết cho 3” B. “ 2 n
∃ ∈  : n +1 không chia hết cho 3”. C. “ 2 n
∃ ∈  : n +1 chia hết cho 3”. D. “ ∃ 2
n∈ : n +1 không chia hết cho 3”.
Câu 4. Mệnh đề nào sau đây sai ?
A. Tam giác ABC đều ⇔ AB = AC và  0 A = 60 .
B. n6 ⇔ n3 và n2 .
C. ABCD là hình chữ nhật ⇔ AC = BD . D. 2
n3 ⇔ n 3, n ∀ ∈ N .
Câu 5. Giá trị của o o
cos60 + sin 30 bằng bao nhiêu? A. 3 B. 3 C. 3 D. 1 2 3
Câu 6.Trong các đẳng thức sau, đẳng thức nào đúng? A. ( o sin 180 −α ) = −cosα . B. ( o sin 180 −α ) = −sinα . C. ( o sin 180 −α ) = sinα . D. ( o sin 180 −α ) = cosα . Câu 7. Cho 1
cos x = . Tính biểu thức 2 2
P = 3sin x + 4 cos x 2 A. 13 . B. 7 . C. 11. D. 15 . 4 4 4 4
Câu 8. Hãy liệt kê các phần tử của tập hợp M = {x∈ N sao cho x lµ ­íc cña } 8 .
A. M = {1;4;16;6 }
4 . B. M = {0;1;4;16;6 } 4 . 1
C. M = {1;2;4; } 8 .
D. M = {0;1;2;4; } 8 .
Câu 9. Trong các tập hợp sau, tập hợp nào là tập rỗng? A. { 2
x ∈  x + 5x − 6 = } 0 . B. { 2
x ∈ 3x − 5x + 2 = } 0 . C. { 2
x ∈ x + x −1 = } 0 . D. { 2
x ∈  x + 5x −1 = } 0 .
Câu 10. Cho A = ( 2 − ;1), B = [ 3
− ;5] . Khi đó A∩ B là tập hợp nào sau đây? A. ( 2 − ;1) . B. [ 2; − 5] . C. [ 2; − ] 1 . D. ( 2; − 5].
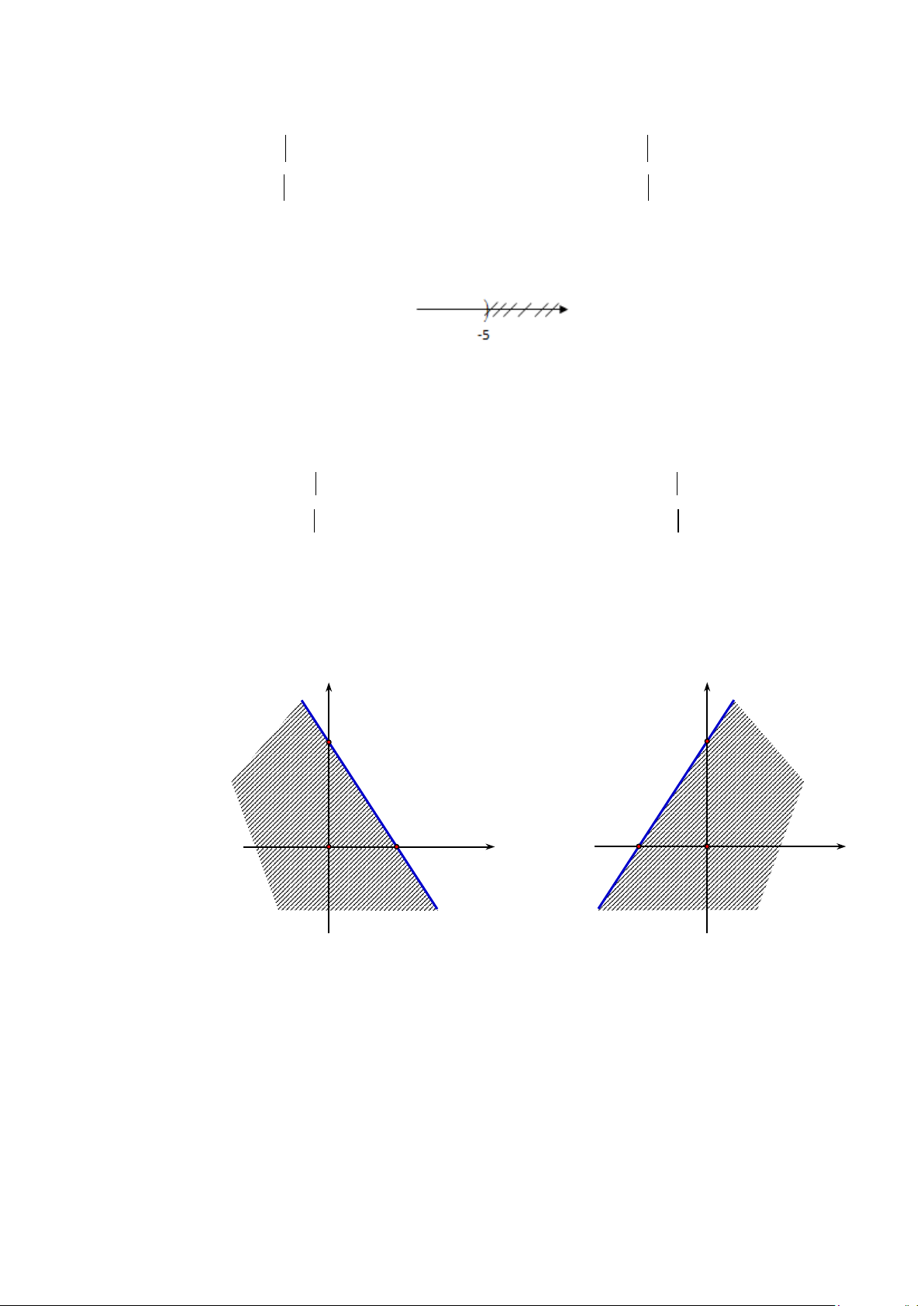
Câu 11. Cho tập X có biểu diễn trên trục số như hình sau:
Khẳng định nào sau đây đúng.
A. X là khoảng, X = ( 5 − ;+ ∞) .
B. X là khoảng, X = (−∞;−5).
C. X là nửa khoảng, X = (−∞;−5] .
D. X là nửa khoảng, X = (−∞;−5].
Câu 12. Cho tập hợp A = [ 3
− ;5]. Viết lại tập hợp A bằng cách chỉ ra tính chất đặc trưng.
A. A = {x∈ −3 ≤ x ≤ } 5 .
B. A = {x∈ −3 < x < } 5 .
C. A = {x∈ −3 ≤ x ≤ } 5 .
D. A = {x∈ −3 ≤ x ≤ } 5 .
Câu 13. Cặp số (1; – )
1 là nghiệm của bất phương trình nào sau đây?
A. x + y – 3 > 0.
B. –x – y < 0.
C. x + 3y +1< 0 .
D. –x – 3y –1< 0 .
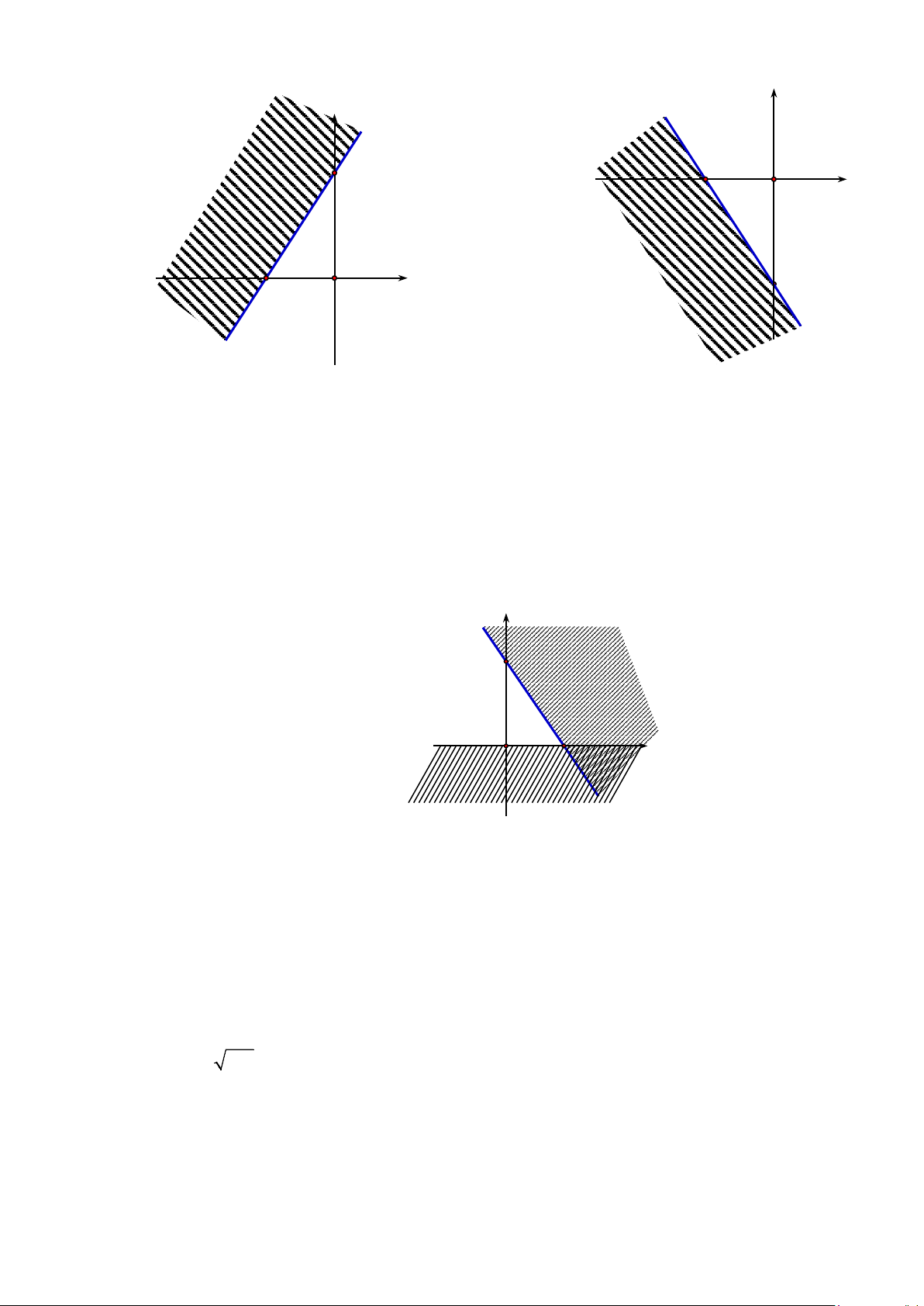
Câu 14. Miền nghiệm của bất phương trình 3x − 2y < 6 − là y y 3 3 A. B. 2 x 2 − O O x 2 y y 2 − 3 O x C. D. 3 2 − O x 3x + y ≥ 9  x ≥ y −3
Câu 15. Miền nghiệm của hệ bất phương trình 
là phần mặt phẳng chứa điểm nào
2y ≥ 8 − x  y ≤ 6 sau đây? A. (0;0) . B. (1;2) . C. (2; ) 1 . D. (8;4).
Câu 16.Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình
nào trong bốn hệ A, B, C, D? y 3 2 x Oy > 0 y > 0 A. . B. . 3  
x + 2y < 6 3
x + 2y < 6 − x > 0 x > 0 C. . D. . 3  
x + 2y < 6 3
x + 2y > 6 −
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1.Cho tam giác ABC có ˆ b 7 c , m c 5 c , m A 120° = = = . Khi đó:
a) a = 127 cm
c) cosB ≈ 0,21
b) cosC ≈ 0,91
d) R ≈ 6,03( cm)
Câu 2. Cho các tập hợp A ={0;1;2;3;4}; B ={0;1;2};C ={ 3 − ;0;1;2}. Khi đó:
a) A \ B = {3;4}
c) A∪ (C \ B) = { 3 − ;0;1;4}
b) (A∩C) \ B = ∅ d) C B = A {1;3;4} 3
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2
Câu 1: Bạn An kinh doanh hai mặt hàng hanhmade là vòng tay và vòng đeo cổ. Mỗi vòng tay
làm trong 4 giờ, bán được 40 000 đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 000. Mỗi
tuần bạn an bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong một
tuần An cần dùng để bán được ít nhất 400 000 đồng.
Câu 2. Cho hai tập hợp A = ( ; −∞ − ]
3 ∪[4;+∞] và[m −1;m + 2),m∈ Z . Tìm tổng các giá trị
của m để A ∩ B = ∅ . PHẦN IV.Tự luận: Câu 1:
Cho hai tập hợp A = {x∈ R 2 − < x < } 7 và B = ( ;
−∞ 5) . Tìm các tập hợp A∩ B, A∪ . B 2
Câu 2:Cho góc α thỏa mãn α − α α + tanα 3sin 2cos .sin 1
= 2 . Tính giá trị của biểu thức P = . 2 2 3cos α − 4sin α
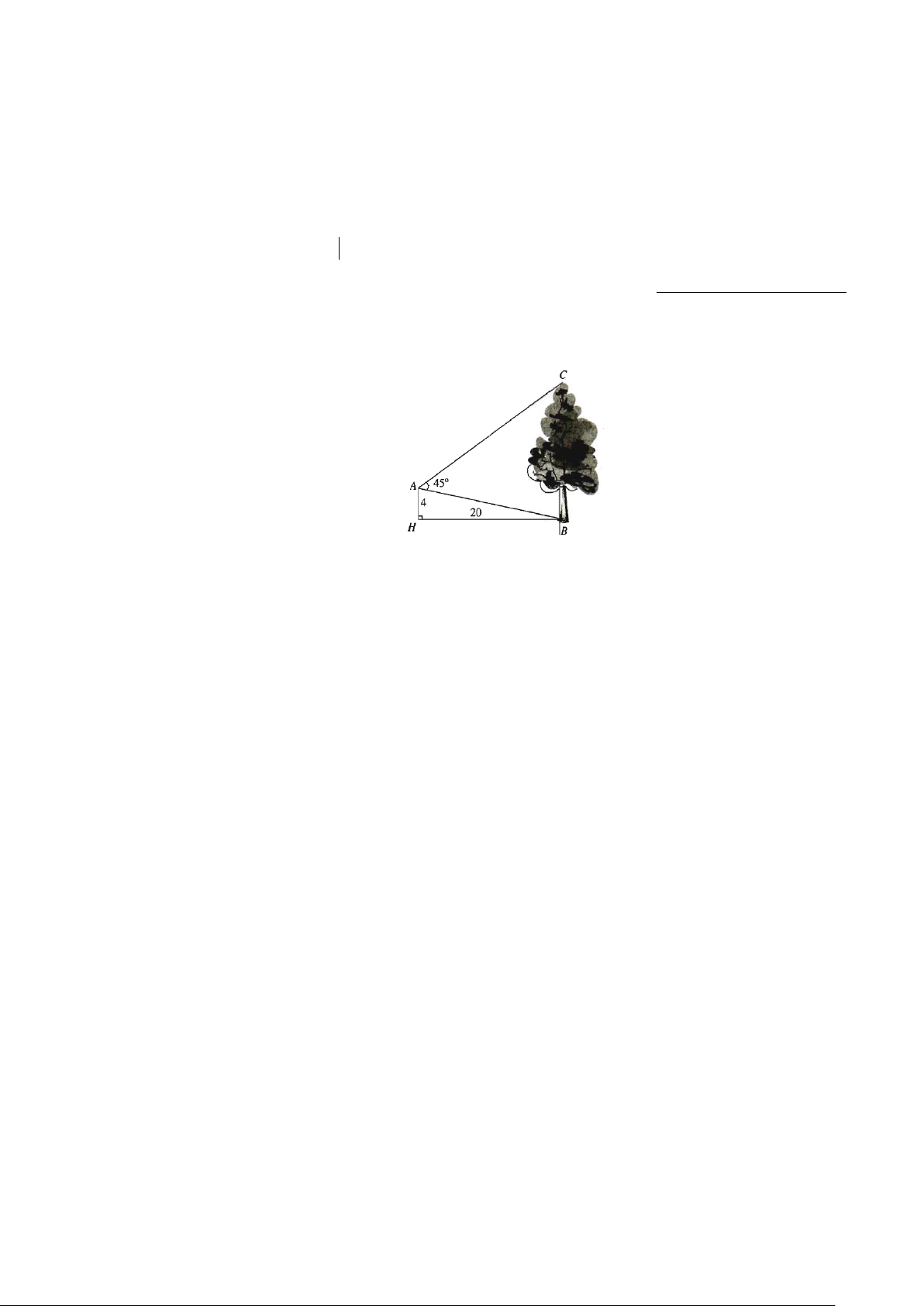
Câu 3: Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết AH = 4m , HB = 20m , 
BAC = 45° . Tính chiều cao của cây ( kết quả làm tròn đến chữ số hàng phần trăm).
------------Hết----------
- Thí sinh không được sử dụng tài liệu;
- Giám thị không giải thích gì thêm. 4
SỞ GD&ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THPT KẺ SẶT NĂM HỌC 2024 - 2025 MÔN:TOÁN KHỐI 10 ĐỀ CHÍNH THỨC
Thời gian làm bài:90 phút không kể thời gian phát đề
( Đề thi có04 .trang)
Họ và tên học sinh:……………………….Lớp:……Số báo danh……….. Mã đề:102
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 16
Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1.Trong các đẳng thức sau, đẳng thức nào đúng? A. ( o sin 180 −α ) = −cosα . B. ( o sin 180 −α ) = −sinα . C. ( o sin 180 −α ) = sinα . D. ( o sin 180 −α ) = cosα . Câu 2. Cho 1
cos x = . Tính biểu thức 2 2
P = 3sin x + 4 cos x 2 A. 13 . B. 7 . C. 11. D. 15 . 4 4 4 4
Câu 3. Hãy liệt kê các phần tử của tập hợp M = {x∈ N sao cho x lµ ­íc cña } 8 .
A. M = {1;4;16;6 }
4 . B. M = {0;1;4;16;6 } 4 .
C. M = {1;2;4; } 8 .
D. M = {0;1;2;4; } 8 .
Câu 4. Trong các tập hợp sau, tập hợp nào là tập rỗng? A. { 2
x ∈  x + 5x − 6 = } 0 . B. { 2
x ∈ 3x − 5x + 2 = } 0 . C. { 2
x ∈ x + x −1 = } 0 . D. { 2
x ∈  x + 5x −1 = } 0 .
Câu 5. Cho A = ( 2 − ;1), B = [ 3
− ;5] . Khi đó A∩ B là tập hợp nào sau đây? A. ( 2 − ;1) . B. [ 2; − 5] . C. [ 2; − ] 1 . D. ( 2; − 5].
Câu 6. Mệnh đề là:
A. Câu cảm thán B. Một khẳng định chỉ có thể đúng hoặc sai
C. Một khẳng định luôn đúng D. Câu nghi vấn hoặc câu cầu khiến
Câu 7. Câu nào trong các câu sau không phải là mệnh đề?
A. π có phải là một số vô tỷ không? B. 2 + 2 = 5 .
C. 2 là một số hữu tỷ. D. 4 = 2 . 2
Câu 8. Phủ định của mệnh đề: “ 2 n
∀ ∈  : n +1 không chia hết cho 3” là: A. “ 2 n
∀ ∈  : n +1 chia hết cho 3” B. “ 2 n
∃ ∈  : n +1 không chia hết cho 3”. C. “ 2 n
∃ ∈  : n +1 chia hết cho 3”. D. “ ∃ 2
n∈ : n +1 không chia hết cho 3”.
Câu 9. Mệnh đề nào sau đây sai ?
A. Tam giác ABC đều ⇔ AB = AC và  0 A = 60 . 1
B. n6 ⇔ n3 và n2 .
C. ABCD là hình chữ nhật ⇔ AC = BD . D. 2
n3 ⇔ n 3, n ∀ ∈ N .
Câu 10. Giá trị của o o
cos60 + sin 30 bằng bao nhiêu? A. 3 B. 3 C. 3 D. 1 2 3
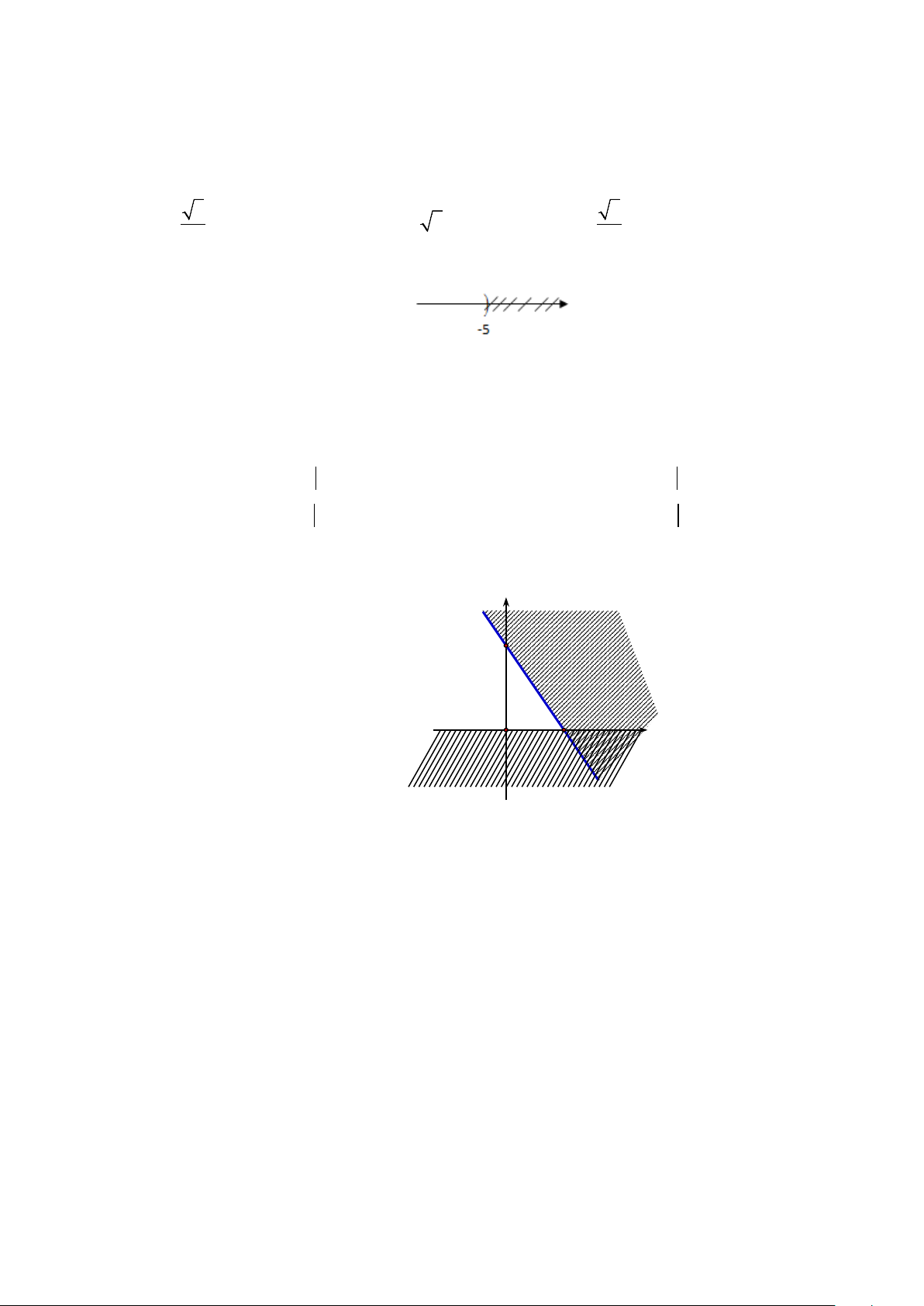
Câu 11. Cho tập X có biểu diễn trên trục số như hình sau:
Khẳng định nào sau đây đúng.
A. X là khoảng, X = ( 5 − ;+ ∞) .
B. X là khoảng, X = (−∞;−5).
C. X là nửa khoảng, X = (−∞;−5] .
D. X là nửa khoảng, X = (−∞;−5].
Câu 12. Cho tập hợp A = [ 3
− ;5]. Viết lại tập hợp A bằng cách chỉ ra tính chất đặc trưng.
A. A = {x∈ −3 ≤ x ≤ } 5 .
B. A = {x∈ −3 < x < } 5 .
C. A = {x∈ −3 ≤ x ≤ } 5 .
D. A = {x∈ −3 ≤ x ≤ } 5 .
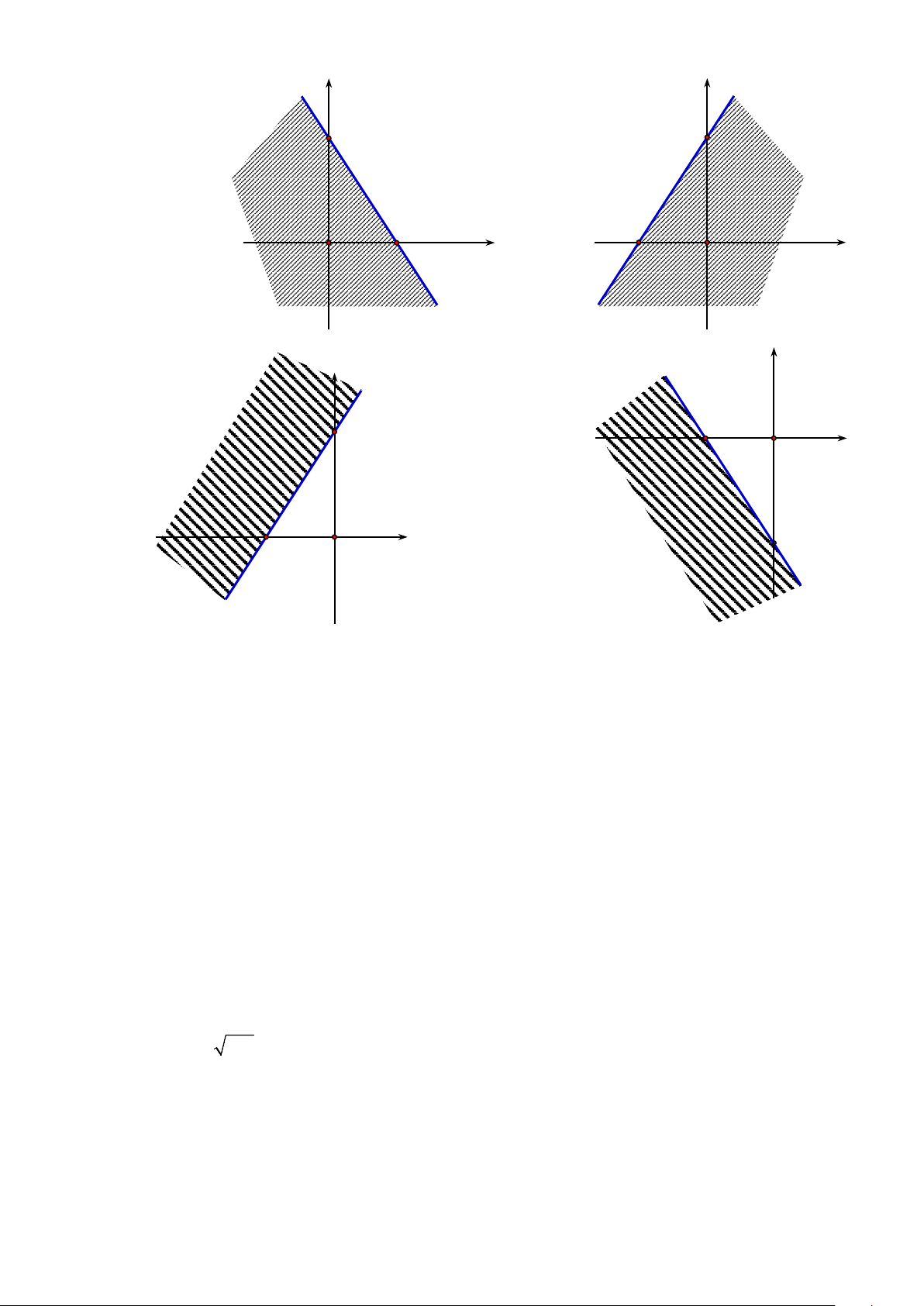
Câu 13.Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình
nào trong bốn hệ A, B, C, D? y 3 2 x Oy > 0 y > 0 A. . B. . 3  
x + 2y < 6 3
x + 2y < 6 − x > 0 x > 0 C. . D. . 3  
x + 2y < 6 3
x + 2y > 6 −
Câu 14. Cặp số (1; – )
1 là nghiệm của bất phương trình nào sau đây?
A. x + y – 3 > 0.
B. –x – y < 0.
C. x + 3y +1< 0 .
D. –x – 3y –1< 0 .
Câu 15. Miền nghiệm của bất phương trình 3x − 2y < 6 − là 2 y y 3 3 A. B. 2 x 2 − O O x y y 2 − 3 O x C. D. 3 2 − O x 3x + y ≥ 9  x ≥ y −3
Câu 16. Miền nghiệm của hệ bất phương trình 
là phần mặt phẳng chứa điểm nào
2y ≥ 8 − x  y ≤ 6 sau đây? A. (0;0) . B. (1;2) . C. (2; ) 1 . D. (8;4).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho các tập hợp A ={0;1;2;3;4}; B ={0;1;2};C ={ 3 − ;0;1;2}. Khi đó:
a) A \ B = {3;4}
c) A∪ (C \ B) = { 3 − ;0;1;4}
b) (A∩C) \ B = ∅ d) C B = A {1;3;4}
Câu 2.Cho tam giác ABC có ˆ b 7 c , m c 5 c , m A 120° = = = . Khi đó:
a) a = 127 cm
c) cosB ≈ 0,21
b) cosC ≈ 0,91
d) R ≈ 6,03( cm)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2
Câu 1. Cho hai tập hợp A = ( ; −∞ − ]
3 ∪[4;+∞] và[m −1;m + 2),m∈ Z . Tìm tổng các giá trị
của m để A ∩ B = ∅ . 3
Câu 2: Bạn An kinh doanh hai mặt hàng hanhmade là vòng tay và vòng đeo cổ. Mỗi vòng tay
làm trong 4 giờ, bán được 40 000 đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 000. Mỗi
tuần bạn an bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong một
tuần An cần dùng để bán được ít nhất 400 000 đồng. PHẦN IV.Tự luận: Câu 1:
Cho hai tập hợp A = {x∈ R 2 − < x < } 7 và B = ( ;
−∞ 5) . Tìm các tập hợp A∩ B, A∪ . B 2
Câu 2,Cho góc α thỏa mãn α − α α + tanα 3sin 2cos .sin 1
= 2 . Tính giá trị của biểu thức P = . 2 2 3cos α − 4sin α
Câu 3: Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết AH = 4m , HB = 20m , 
BAC = 45° . Tính chiều cao của cây ( kết quả làm tròn đến chữ số hàng phần trăm).
------------Hết----------
- Thí sinh không được sử dụng tài liệu;
- Giám thị không giải thích gì thêm. 4
SỞ GD&ĐT HẢI DƯƠNG ĐA- HD CHẤM
TRƯỜNG THPT KẺ SẶT
ĐỀ KIỂM TRA GIỮA KỲ I NĂM HỌC: 2024 - 2025 MÔN: TOÁN - LỚP: 10 Phần I II Số câu 16 2 Câu\Mã đề 101 102 1 B C 2 A A 3 B A 4 C C 5 D A 6 C B 7 A A 8 A B 9 C C 10 A D 11 B B 12 A A 13 C C 14 B C 15 D B 16 C C 1 SSDD DDSS 2 DDSS SSDD 1 32 2 2 2 32
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 10
https://toanmath.com/de-thi-giua-hk1-toan-10
SỞ GD& ĐT HẢI DƯƠNG
ĐÁP ÁN – THANG ĐIỂM
TRƯỜNG THPT KẺ SẶT
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
(Đáp án - Thang điểm có 02 trang)
NĂM HỌC: 2024 - 2025
MÔN: TOÁN - KHỐI 10 MÃ ĐỀ: 101+102
IV. Tự luận (3,0 điểm) Câu Ý Nội dung Điểm
Cho hai tập hợp A = {x∈ R 2 − < x < } 7 và B = ( ;
−∞ 5) . Tìm các tập hợp 1
A∩ B, A∪ . B Ta có A = ( 2; − 7) 0,25
A∩ B = ( 2; − 5) 0,5 A∪ B = ( ; −∞ 7) 0,25
Cho góc α thỏa mãn tanα = 2 . Tính giá trị của biểu thức 2 2 3sin α − 2cosα.sinα +1 P = . 2 2 3cos α − 4sin α
Ta có tanα = 2 nên cosα ≠ 0 . 0.5
Chia cả tử và mẫu của P cho 2 cos α ta được 2 2 0.5 3tan α − 2 tanα +1+ tan α P = = 1 − 2 3− 4 tan α 1
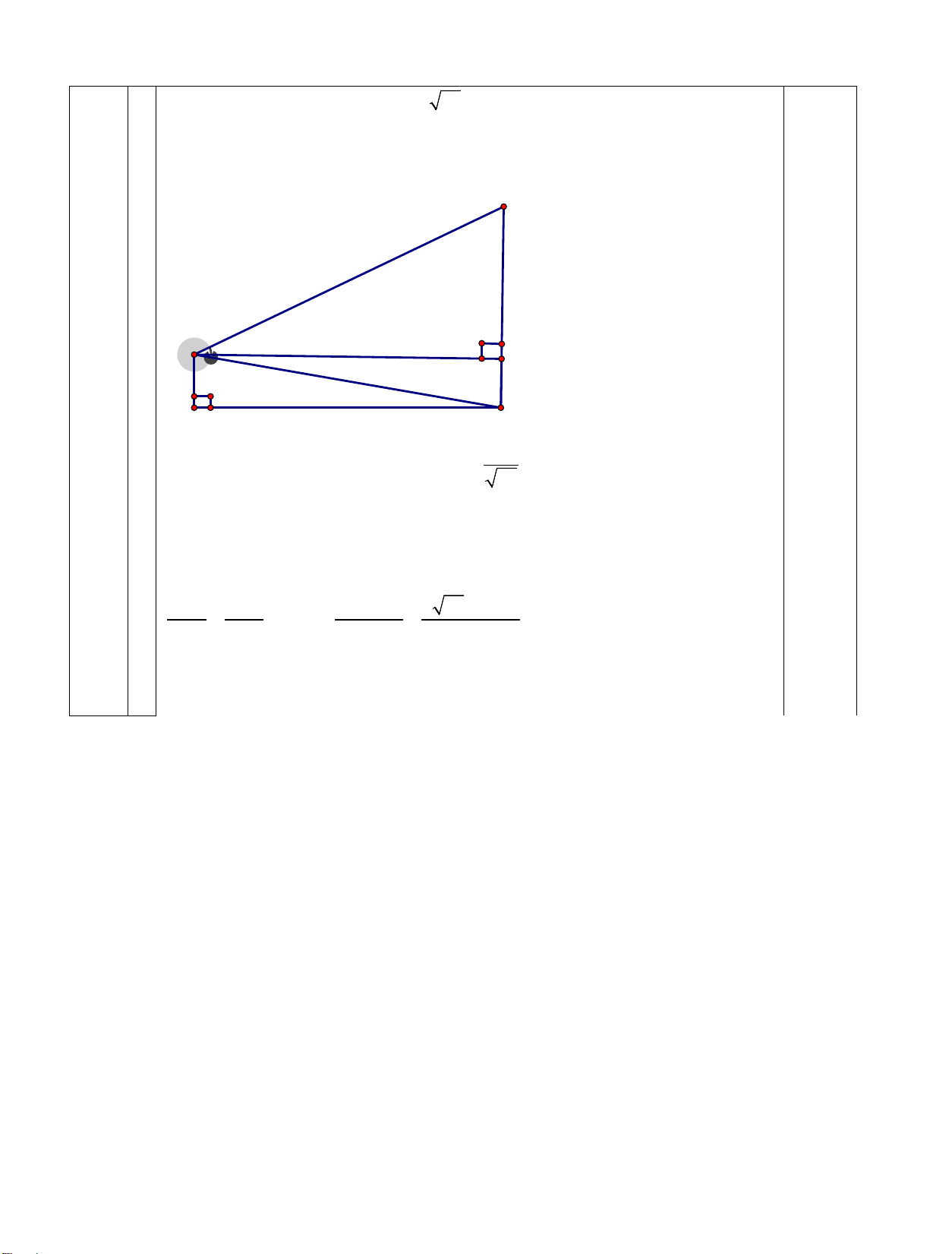
Áp dụng định lí Pitago ta có AB = 4 26 0,25
Kẻ đường cao AK, K ∈ BC . C A 45° K 3 H B Trong tam giác ABK có 1
BK = 4 ⇒ cos B = . Khi đó góc  0 B ≈ 79 26 0,25 Do đó 0 C ≈ 56
Áp dụng định lí sin cho tam giác ABC ta có 0 AB BC A .
B sin A 4 26.sin 45 = ⇔ BC = = ≈ 17,4m 0,25 0 sin C sin A sin C sin 56 Vậy cây cao gần 17,4m 0,25 GIÁO VIÊN RA ĐỀ BAN GIÁM HIỆU PHÓ HIỆU TRƯỞNG Lê Quang Hòa Vũ Văn Phước 2
Document Outline

  • KTGHKI_TOÁN 10_ MĐ 101
  • KTGHKI_TOÁN 10_ MĐ 102
  • KTGKI_ DA,HDC-TOÁN K10
    • Sheet1
  • KTGKI-ĐA,HDC-TOÁN K10 -MĐ101+102