SỞ GD&ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA GIỮA KỲ I - NĂM HỌC 2024-2025
TRƯỜNG THPT NGUYỄN VĂN CỪ
MÔN: TOÁN - Lớp: 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề ( Đề có 03 trang)
Họ và tên thí sinh: .................................................................... Mã đề 101
Số báo danh: .............................................................................
PHẦN I. Trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 16. Mỗi câu hỏi
học sinh chỉ chọn một phương án.
Câu 1. Đổi sang đơn vị radian góc có số đo 216° ta được A. 4π . B. 6π . C. 3π . D. 7π . 3 5 5 6
Câu 2. Phương trình sin x = m có nghiệm khi và chỉ khi 2 1 1 A. m ∈[ 2; − 2] . B. m∈[ 1; − ] 1 . C. m  ;  ∈ −  . D. m ∈  . 2 2  
Câu 3. Cho dãy số (u biết 2n + 5 u =
Số 7 là số hạng thứ mấy của dãy số? n . n ) , 5n − 4 12 A. 8. B. 9. C. 10. D. 6.
Câu 4. Tập xác định của hàm số sin = x y là: 1− cos x A. kπ D  \  |  = k ∈ .
B. D =  \{k2π | k ∈ }  . 2    C. D π
=  \{kπ | k ∈ }  . D. D  \  kπ |  = + k ∈ . 2   
Câu 5. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , I lần lượt là trung điểm của SA,
BC , điểm G nằm giữa S và I sao cho SG 3
= . Giao điểm của đường thẳng MG với mặt phẳng SI 5 ( ABCD) là
A. Giao điểm của đường thẳng MG và đường thẳng AB .
B. Giao điểm của đường thẳng MG và đường thẳng AI .
C. Giao điểm của đường thẳng MG và đường thẳng BC .
D. Giao điểm của đường thẳng MG và đường thẳng CD .
Câu 6. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , N lần lượt là trung điểm của AD
và BC . Giao tuyến của (SMN ) và (SAC) là đường thẳng
A. SO (O là tâm của hình bình hành ABCD ). B. SF ( F là trung điểm của CD ).
C. SK ( K là trung điểm của AB ). D. SD .
Câu 7. Cho mặt phẳng (α ) và đường thẳng d ⊄ (α ) . Khẳng định nào sau đây là sai?
A. Nếu d ∩(α ) = A và d′ ⊂ (α ) thì d và d′ hoặc cắt nhau hoặc chéo nhau.
B. Nếu d // (α ) thì trong (α ) tồn tại đường thẳng ∆ sao cho ∆ // d .
C. Nếu d // c; c ⊂ (α ) thì d // (α ) .
D. Nếu d // (α ) và b ⊂ (α ) thì b // d . Trang 1 /3– Mã đề 101
Câu 8. Công thức nào sau đây đúng? A. cos( α  π − ) = −cosα . B. cos α  + =   sinα.  2  C. sin (π  π +α ) = sinα. D. cos α  − =   sinα.  2 
Câu 9. Phương trình  π cot  x + =   3 có nghiệm là :  3  A. π
x = + kπ (k ∈)
. B. x = kπ (k ∈) . 3 C. π π
x = + kπ (k ∈) .
D. x = − + kπ (k ∈) . 6 6
Câu 10. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của SB. Giao
điểm của DM và (SAC) là
A. Giao điểm của DM và SO.
B. Giao điểm của DM và AC.
C. Giao điểm của DM và SC.
D. Giao điểm của DM và SA. π
Câu 11. Cho α thỏa mãn 3 π < α <
. Hãy chọn kết quả đúng trong các kết quả sau đây. 2
A. cosα < 0.
B. sinα > 0.
C. cotα < 0. D. tanα < 0.
Câu 12. Khẳng định nào sau đây đúng? A.  π  3 1  π cos x − = cos x −    sin x . B. 3 1 cos x − = cos x +   sin x .  3  2 2  3  2 2 C.  π  1 3  π cos x − = cos x +    sin x . D. 1 3 cos x − = cos x −   sin x .  3  2 2  3  2 2
Câu 13. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.
B. Hai đường thẳng có một điểm chung thì chúng có vô số điểm chung khác.
C. Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.
D. Hai đường thẳng song song khi và chỉ khi chúng không điểm chung.
Câu 14. Trong các dãy số (u
u sau, dãy số nào là dãy số tăng?
n ) cho bởi số hạng tổng quát n
A. u = 2 .n B. u = ( 2 − )n C. 2 u = D. 3 u = n . n . n . n 3n n
Câu 15. Công thức lượng giác nào dưới đây đúng? A. 1 cos cos cos a + b  a b a b 1  .cos −  + = .
B. cos a + cosb = cos(a + b).cos(a −b). 2 2  2      2
C. cos a + cosb = 2cos(a + b).cos(a −b). D. cos cos
2cos a + b  a b a b .cos −  + =  . 2  2     
Câu 16. Phương trình 3 + tan x = 0 có nghiệm là: A. π 2π π
x = + k2π; x = + k2π ( k ∈).
B. x = − + kπ (k ∈) . 3 3 3 C. π 4π π
x = − + k2π; x =
+ k2π (k ∈).
D. x = + kπ (k ∈) . 3 3 3
PHẦN II. Trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, học sinh chọn đúng hoặc sai.
Câu 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy điểm P sao
cho BP = 2PD. Khi đó :
a) MN // ( ABD) . Trang 2 /3– Mã đề 101 b) MP//CD .
c) Gọi I = CD ∩(MNP) , ba điểm I, N, P thẳng hàng.
d) Giao tuyến của hai mặt phẳng (MNP) và ( ABD)là đường thẳng qua điểm P và song song với AB. Câu 2: Cho 3
sinα = và 90° < α <180° . Xét tính đúng, sai của các mệnh đề sau: 5 a) 4 cosα − = . 5 b) 2 2 sin 2α + cos 2α = 2
c) sin 3α − sinα = 3sinα 2 2cos α −1 α − α d) Biểu thức cot 2 tan − = = a E
(với a là phân số tối giản và * a,b∈ ). tanα + 3tan (90° −α ) b b
Khi đó a + b = 55 .
PHẦN III. Trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 2
Câu 1: Một vận động viên bắn súng nằm trên mặt đất theo phương vuông góc với một bức tường thẳng
đứng để ngắm bắn các mục tiêu khác nhau trên bức tường đó. Vận động viên bắn trúng một mục tiêu
cách mặt đất 30m tại một góc ngắm (góc hợp bởi phương ngắm với phương ngang). Nếu vẫn giữ nguyên
phương nằm bắn đó và giảm góc ngắm đi một nửa thì vận động viên bắn trúng mục tiêu cách mặt đất
12m. Tính khoảng cách từ vận động viên đến bức tường. (Kết quả được làm tròn đến hàng phần mười)
Câu 2: Cho hàm số: y = cos 2x − 2cos x + 4 có giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M và m .
Tính tích M.m ? PHẦN IV. Tự luận Câu 1: Cho 5 π sinα =
và < α < π . Tính giá trị của cosα và tan 2α . 13 2
Câu 2: a) Giải phương trình: 3 cos5x = . 2
b) Tìm nghiệm của phương trình:  π tan  x + =   1 trên đoạn [ π − ;2π ].  5 
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD.
a) Chứng minh rằng: MN // (SBC) .
b) Gọi G ; G lần lượt là trọng tâm các tam giác ACD và tam giác SCD. 1 2
Chứng minh G G // SAC . 1 2 ( )
----------------HẾT---------------
Học sinh không được sử dụng tài liệu. Trang 3 /3– Mã đề 101 SỞ GD&ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA GIỮA KỲ I - NĂM HỌC 2024-2025
TRƯỜNG THPT NGUYỄN VĂN CỪ
MÔN: TOÁN - Lớp: 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề ( Đề có 03 trang)
Họ và tên thí sinh: .................................................................... Mã đề 102
Số báo danh: .............................................................................
PHẦN I. Trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 16. Mỗi câu hỏi
học sinh chỉ chọn một phương án.
Câu 1. Trong các dãy số (u
u sau, dãy số nào là dãy số tăng?
n ) cho bởi số hạng tổng quát n A. 2 u = B. 3 u = C. u = ( 2 − )n D. u = n 2 .n n . n . n . 3n n
Câu 2. Công thức lượng giác nào dưới đây đúng?
A. cos a + cosb = 2cos(a + b).cos(a −b). B. cos cos
2cos a + b  a b a b .cos −  + =  . 2  2      C. 1 cos  a + b   a −
a + cosb = cos(a + b).cos(a − b). D. 1 cos cos cos b a b  .cos  + = . 2 2 2  2     
Câu 3. Cho dãy số (u biết 2n + 5 u =
Số 7 là số hạng thứ mấy của dãy số? n . n ) , 5n − 4 12 A. 10. B. 8. C. 9. D. 6.
Câu 4. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , N lần lượt là trung điểm của AD
và BC . Giao tuyến của (SMN ) và (SAC) là đường thẳng A. SD .
B. SO (O là tâm của hình bình hành ABCD ).
C. SK ( K là trung điểm của AB ).
D. SF ( F là trung điểm của CD ).
Câu 5. Phương trình sin x = m có nghiệm khi và chỉ khi 2 1 1 A. m ∈[ 2; − 2] .
B. m ∈  . C. m  ;  ∈ −  . D. m∈[ 1; − ] 1 . 2 2   π
Câu 6. Cho α thỏa mãn 3 π < α <
. Hãy chọn kết quả đúng trong các kết quả sau đây. 2
A. cosα < 0.
B. cotα < 0.
C. sinα > 0. D. tanα < 0.
Câu 7. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.
B. Hai đường thẳng có một điểm chung thì chúng có vô số điểm chung khác.
C. Hai đường thẳng song song khi và chỉ khi chúng không điểm chung.
D. Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.
Câu 8. Phương trình 3 + tan x = 0 có nghiệm là: A. π π
x = − + kπ (k ∈) .
B. x = + kπ (k ∈) . 3 3 C. π 4π π π
x = − + k2π; x = + k2π (k ∈ 2 ).
D. x = + k2π; x = + k2π ( k ∈). 3 3 3 3
Câu 9. Tập xác định của hàm số sin = x y là: 1− cos x A. π D  \  kπ |  = + k ∈ .
B. D =  \{k2π | k ∈ }  . 2    Trang 1 /3– Mã đề 102 C. D kπ
=  \{kπ | k ∈ }  . D. D  \  |  = k ∈ . 2   
Câu 10. Cho mặt phẳng (α ) và đường thẳng d ⊄ (α ) . Khẳng định nào sau đây là sai?
A. Nếu d // (α ) và b ⊂ (α ) thì b // d .
B. Nếu d // (α ) thì trong (α ) tồn tại đường thẳng ∆ sao cho ∆ // d .
C. Nếu d // c; c ⊂ (α ) thì d // (α ) .
D. Nếu d ∩(α ) = A và d′ ⊂ (α ) thì d và d′ hoặc cắt nhau hoặc chéo nhau.
Câu 11. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của SB. Giao
điểm của DM và (SAC) là
A. Giao điểm của DM và SA.
B. Giao điểm của DM và SO.
C. Giao điểm của DM và AC.
D. Giao điểm của DM và SC.
Câu 12. Phương trình  π cot  x + =   3 có nghiệm là :  3  A. π
x = + kπ (k ∈) .
B. x = kπ (k ∈) . 3 C. π π
x = + kπ (k ∈) .
D. x = − + kπ (k ∈) . 6 6
Câu 13. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , I lần lượt là trung điểm của SA ,
BC , điểm G nằm giữa S và I sao cho SG 3
= . Giao điểm của đường thẳng MG với mặt phẳng SI 5 ( ABCD) là
A. Giao điểm của đường thẳng MG và đường thẳng CD .
B. Giao điểm của đường thẳng MG và đường thẳng BC .
C. Giao điểm của đường thẳng MG và đường thẳng AI .
D. Giao điểm của đường thẳng MG và đường thẳng AB .
Câu 14. Đổi sang đơn vị radian góc có số đo 216° ta được A. 3π . B. 7π . C. 4π . D. 6π . 5 6 3 5
Câu 15. Khẳng định nào sau đây đúng? A.  π  1 3  π cos x − = cos x +    sin x . B. 3 1 cos x − = cos x −   sin x .  3  2 2  3  2 2 C.  π  1 3  π cos x − = cos x −    sin x . D. 3 1 cos x − = cos x +   sin x .  3  2 2  3  2 2
Câu 16. Công thức nào sau đây đúng? A.  π cos α  − =   sinα. B. cos( α − ) = −cosα  2  C.  π cos α  + =   sinα.
D. sin (π +α ) = sinα.  2 
PHẦN II. Trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, học sinh chọn đúng hoặc sai.
Câu 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, BC. Trên đoạn BD lấy điểm P sao
cho BP = 2PD. Khi đó : a) MP//CD .
b) MN // ( ABD) . Trang 2 /3– Mã đề 102
c) Gọi I = CD ∩(MNP) , ba điểm I, N, P thẳng hàng.
d) Giao tuyến của hai mặt phẳng (MNP) và ( ABD)là đường thẳng qua P và song song với AB. Câu 2: Cho 3
sinα = và 90° < α <180° . Xét tính đúng, sai của các mệnh đề sau: 5 a) 4 cosα − = . 5 b) 2 2 sin 2α + cos 2α = 2
c) sin 3α − sinα = 3sinα 2 2cos α −1 α − α d) Biểu thức cot 2 tan − = = a E
(với a là phân số tối giản và * a,b∈ ). tanα + 3tan (90° −α ) b b
Khi đó a + b = 55 .
PHẦN III. Trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 2
Câu 1: Một vận động viên bắn súng nằm trên mặt đất theo phương vuông góc với một bức tường thẳng
đứng để ngắm bắn các mục tiêu khác nhau trên bức tường đó. Vận động viên bắn trúng một mục tiêu
cách mặt đất 30m tại một góc ngắm (góc hợp bởi phương ngắm với phương ngang). Nếu vẫn giữ nguyên
phương nằm bắn đó và giảm góc ngắm đi một nửa thì vận động viên bắn trúng mục tiêu cách mặt đất
12m. Tính khoảng cách từ vận động viên đến bức tường. (Kết quả được làm tròn đến hàng phần mười)
Câu 2: Cho hàm số: y = cos 2x − 2cos x + 4 có giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M và m .
Tính tích M.m ? PHẦN IV. Tự luận Câu 1: Cho 3 π
cosα = và 3 < α < 2π . Tính giá trị của sinα và tan 2α 4 2
Câu 2: a) Giải phương trình: 1 sin 6x = . 2
b) Tìm nghiệm của phương trình:  π tan  x − =   3 trên đoạn [0;3π ] .  4 
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, K lần lượt là trung điểm của AB và CD.
a) Chứng minh rằng: IK // (SAD).
b) Gọi G ; G lần lượt là trọng tâm các tam giác BCD và SCD. Chứng minh G G // SBD . 1 2 ( ) 1 2
----------------HẾT---------------
Học sinh không được sử dụng tài liệu. Trang 3 /3– Mã đề 102 Phần I II III Số câu 16 2 2 Câu\Mã đề 101 102 103 104 105 106 107 108 1 B D A B B C C B 2 B B C B A B B D 3 A B B A D A C B 4 B B A C B C B C 5 B D A A D D C D 6 A A C D B A C A 7 D D B A D B D C 8 D A B B D B C B 9 D B C D D B D C 10 A A B B A A B C 11 A B C A C C C C 12 C D D D A A C B 13 A C B D A C A D 14 A D A B B C A D 15 D A A B A C D D 16 B A C A C B B B 1
DSDD SDDD DSDD SDDD DSDD SDDD DSDD SDDD 2
DSSS DSSS DSSS DSSS DSSS DSSS DSSS DSSS 1 26,8 26,8 26,8 26,8 26,8 26,8 26,8 26,8 2 17,5 17,5 17,5 17,5 17,5 17,5 17,5 17,5
TRƯỜNG THPT NGUYỄN VĂN CỪ
ĐÁP ÁN ĐỀ KIỂM TRA GIỮA KỲ I NĂM HỌC 2024 - 2025
Môn: TOÁN – Lớp: 11 Phần IV. Tự luận ĐỀ 1 Câu Ý Nội dung Điểm Câu 1 Cho 5 π sinα =
và < α < π . Tính giá trị của biểu thức 1.0 1.0 đ 13 2  12 0.25 2 cosα =  Ta có 2 2  5  144 cos α =1− sin α =1− = 13  ⇒  13    169 c 1 os 2 α = −  3 1
Do π < α < π nên cosα < 0 . Vậy 12 cosα = − 0.25 2 13 Khi đó sinα 5 tanα − = = 0.25 cosα 12 2 tanα 120 tan 2α − = = 0.25 2 1− tan α 119 Câu 2 0.5
1.0 đ a) Giải phương trình sau: 3 cos5x = 2 3 π 0.25 cos5x = ⇔ cos5x = cos 2 6 π
⇔ 5x = ± + k2π 6 π k2π ⇔ x = ± + (k ∈) 0.25 30 5
b) Tìm nghiệm của phương trình:  π 0.5 tan x  + =   1 trên đoạn [ π − ;2π ]  5   π   π  π 0.25 tan x + = 1 ⇔ tan x + =     tan  5   5  4 π π ⇔ x + = + kπ 5 4π ⇔ x = + kπ (k ∈) 20 Do π x ∈[ π − ;2π ] nên 21 39 π kπ 2π − − ≤ + ≤ ⇔ ≤ k ≤ 0.25 20 20 20
Mà k nguyên nên k ∈{ 1, − 0, } 1 19 − π π 21π
Vậy phương trình có 3 nghiệm thỏa mãn là ; ; 20 20 20 Câu 3
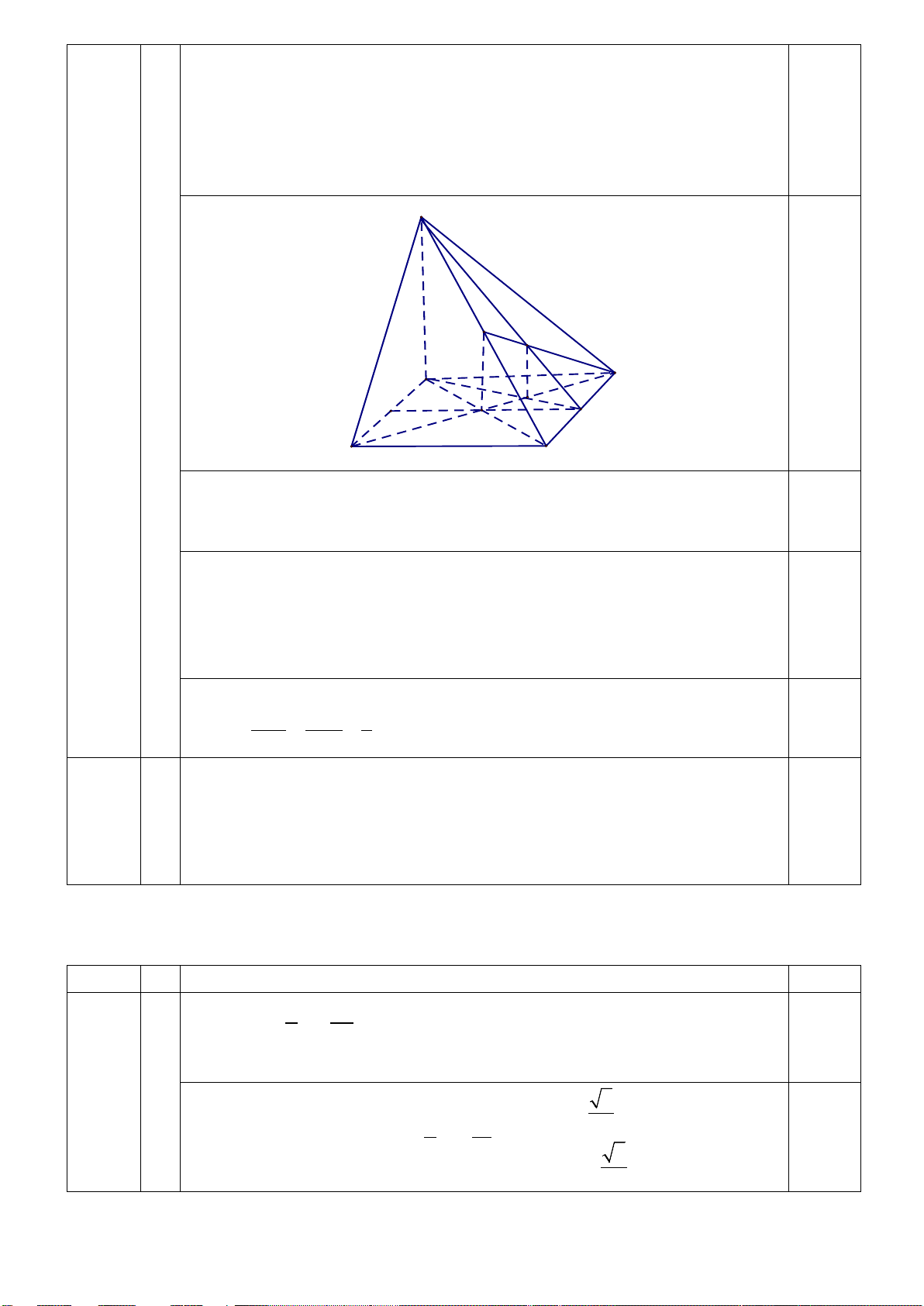
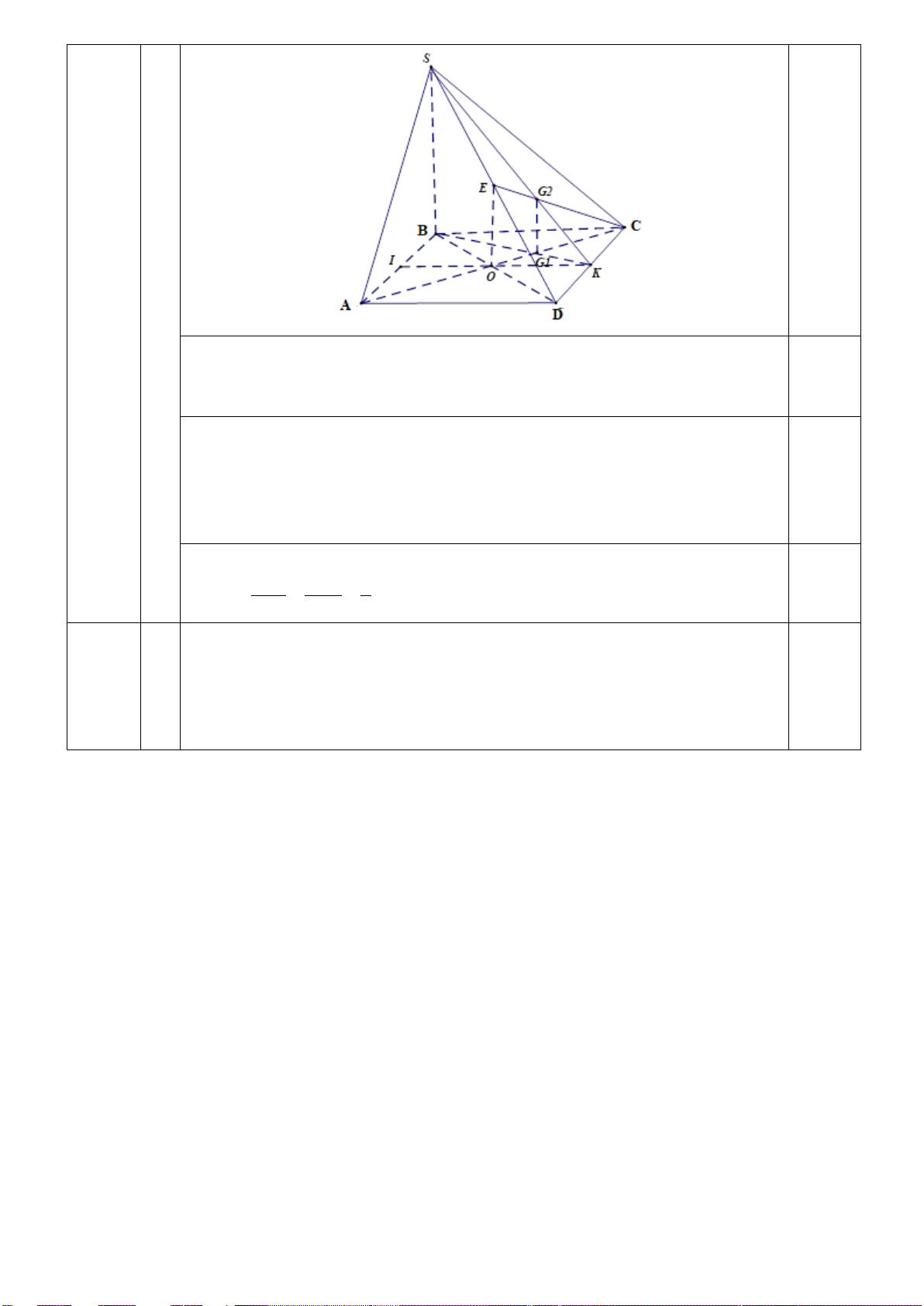
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là 1.0 1 1.0 đ
trung điểm của AB và CD.
a) Chứng minh rằng: MN // (SBC) .
b) Gọi G ; G lần lượt là trọng tâm các tam giác ACD và tam giác 1 2
SCD. Chứng minh G G // SAC . 1 2 ( ) S E G2 A D M G1 O N B C VẼ HÌNH 0.25
+) Do ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD nên MN //BC +) Có 0.25 MN //BC  BC (SBC)  ⊂
 ⇒ MN // (SBC) MN (SBC) ⊄ 
+ Theo tính chất trọng tâm tam giác ta có 0.25 1 NG 2 NG 1 = = ⇒ 1 G 2 G //SA NA NS 3 +) Có 0.25 G G //SA  1 2 SA (SAC)  ⊂  ⇒ 1 G 2 G // (SAC)  1 G 2 G ⊄ (SAC)
Học sinh làm các cách khác nhau mà đúng thì vẫn cho điểm tối đa. ĐỀ 2 Câu Ý Nội dung Điểm Câu 1 π 1.0 1.0 đ Cho 3
cosα = và 3 < α < 2π . Tính giá trị của sinα và tan 2α 4 2  7 0.25 2 sinα = Ta có 2 2 α =1− cos α =1  3  7 sin − = 4  ⇒  4    6 1  7 sinα = −  4 2 0.25
Do 3π < α < 2π nên sinα < 0. Vậy 7 sinα = − 2 4 0.25 Khi đó sinα − 7 tanα = = cosα 3 2 tanα tan 2α = = 3 − 7 0.25 2 1− tan α Câu 2 Giải phương trình sau: 1 sin 6x = 0.5 1.0 đ a) 2 1 π sin 6x 0.25 = ⇔ sin 6x = sin 2 6  π 6x = + k2π  6 ⇔  5π 6x = + k2π  6  π kπ 0.25 x = + (k ∈)  36 3 ⇔   5π kπ x = + (k ∈)  36 3
b) Tìm nghiệm của phương trình:  π tan 0.5 x  − =   3 trên đoạn [ π − ;2π ]  4   π   π  π 0.25 tan x − = 3 ⇔ tan x − =     tan  4   4  3 π π
⇔ x − = + kπ 4 3 7π ⇔ x = + kπ (k ∈) 12 Do π x ∈[0;3π ] nên 7 7 29 0 kπ 3π − ≤ + ≤ ⇔ ≤ k ≤ 0.25 12 12 12
Mà k nguyên nên k ∈{0,1, } 2 7π 19π 31π
Vậy phương trình có 3 nghiệm thỏa mãn là ; ; 12 12 12 Câu 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, K lần lượt là 1.0 1.0 đ
trung điểm của AB và CD.
a) Chứng minh rằng: IK // (SAD)
b) Gọi G ; G lần lượt là trọng tâm các tam giác BCD và SCD. Chứng 1 2
minh G G // SBD 1 2 ( ) 3 VẼ HÌNH 0.25
+) Do ABCD là hình bình hành và I, K lần lượt là trung điểm của AB, CD nên IK //AD +) Có 0.25 IK //AD  AD (SAD) ⊂
 ⇒ IK // (SAD) IK (SAD)  ⊄ 
Theo tính chất trọng tâm tam giác ta có 0.25 1 KG 2 KG 1 = = ⇒ 1 G 2 G //SB KB KS 3 +) Có 0.25 G G //SB  1 2 SB (SBD)  ⊂  ⇒ 1 G 2 G // (SBD)  1 G 2 G ⊄ (SBD)
Học sinh làm các cách khác nhau mà đúng thì vẫn cho điểm tối đa. 4
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 11
https://toanmath.com/de-thi-giua-hk1-toan-11
Document Outline

• Toán 11- GK1- Mã 101
• Toán 11- GK1- Mã 102
• Toán 11_Đáp án trắc nghiệm KTGKI 2024-2025 (mẫu chấm)
  • GK1- Toan 11
• Toán 11- Đáp án Tự luận KT GKI -2024-2025
• XEM THEM - GIUA KY 1 - TOAN 11