


Preview text:
SỞ GD&ĐT KON TUM ĐỀ KIỂM TRA HỌC KÌ I TRƯỜNG THPT CHUYÊN NTT NĂM HỌC 2021-2022 Môn: TOÁN CHUYÊN Lớp: 11 Ngày kiểm tra: 18/12/2021 ĐỀ CHÍNH THỨC
Thời gian: 90 phút (không kể thời gian phát đề)
(Đề gồm có 07 câu, 01 trang) Đề bài
Câu 1 (3.0 điểm). Tính các giới hạn sau: 2n 5 1 2.3n x 1 2 a) lim ; b) lim ; c) lim ; 4n 3 3n 2n 2 x 3 x 9
Câu 2 (3.0 điểm). Tính đạo hàm của các hàm số sau: 5 2 1 2 x 2x 3 a) 4 3 y x x x ; b) y ; c) 2 y x x 3 ; 4 3 10 x 1
Câu 3 (1.0 điểm). Trong mặt phẳng tọa độ Oxy , cho đường tròn (C) có phương trình
x 2 y 2 1 2 6 và điểm (
A 4;5) . Xác định phương trình đường tròn (C ') là ảnh của (C)
qua phép tịnh tiến theo AO .
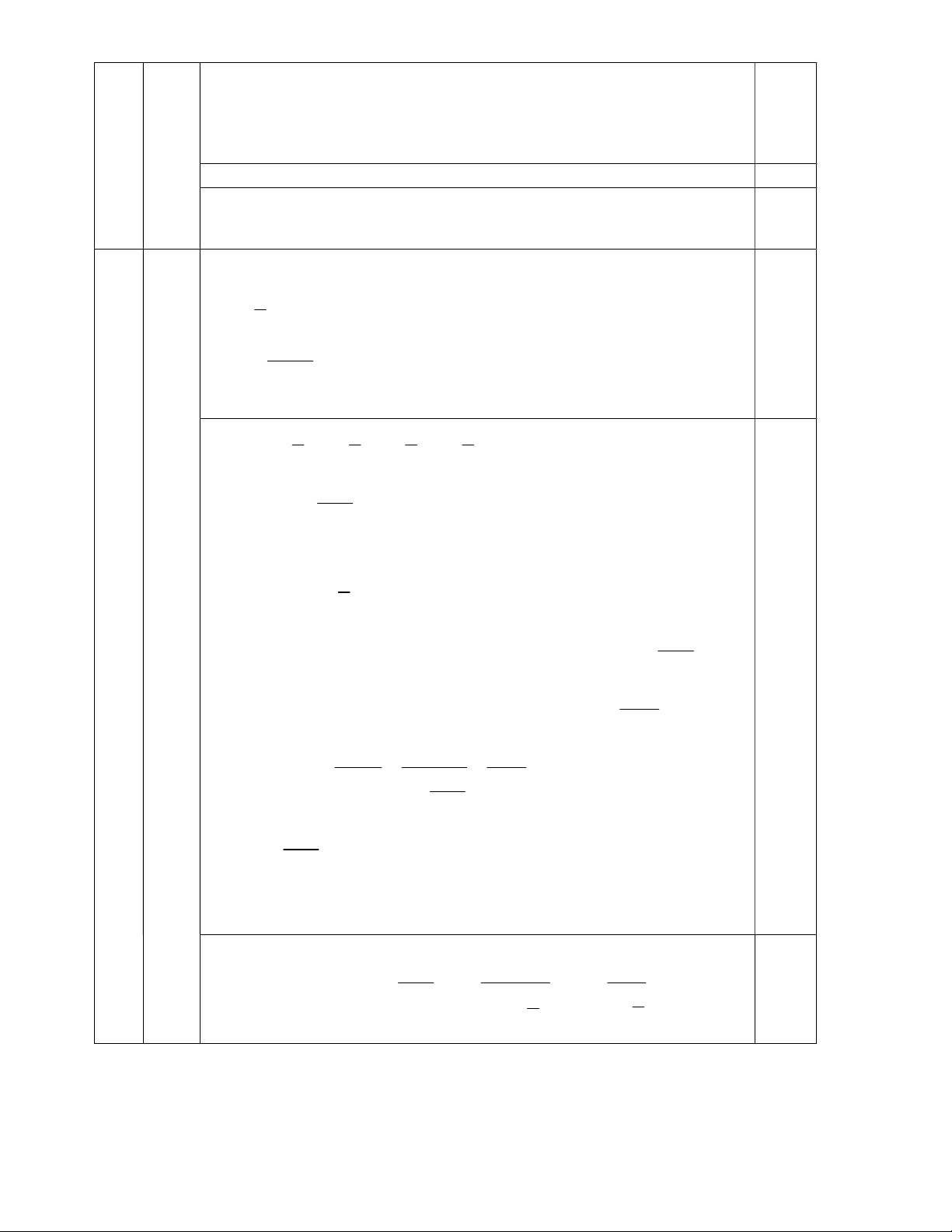
Câu 4 (1.5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . SA
vuông góc với mặt phẳng đáy và SA a 2 .
a) Chứng minh CD vuông góc với mặt phẳng (SAD) và tính theo a diện tích tam giác SCD .
b) Xác định và tính góc giữa đường thẳng SC với mặt phẳng (ABCD) . x 1
Câu 5 (0.5 điểm). Cho hàm số y f (x)
có đồ thị (C) . Viết phương trình tiếp tuyến của x 2
đồ thị (C) tại giao điểm của đồ thị (C) với trục hoành.
Câu 6 (0.5 điểm). Học kì 1 năm học 2021-2022 lớp 11 Toán có tổng cộng 11 học sinh đạt giải
trong các cuộc thi, trong đó: 3 học sinh đạt giải nhất, 5 học sinh đạt giải nhì và 3 học sinh đạt giải
ba. Giáo viên chủ nhiệm chọn ngẫu nhiên 2 học sinh. Hỏi giáo viên chủ nhiệm có bao nhiêu cách
chọn để 2 học sinh đó có ít nhất một em đạt giải nhất. 1 u 1 2
Câu 7 (0.5 điểm). Cho dãy số u xác định bởi công thức truy hồi , với n 1. Biết n 1 u n 1 2 u n
dãy số u có giới hạn hữu hạn khi n . Tìm giới hạn đó. n
----------------- HẾT ----------------- Trang 1
SỞ GD&ĐT KON TUM ĐỀ KIỂM TRA HỌC KÌ I TRƯỜNG THPT CHUYÊN NTT NĂM HỌC 2021-2022 Môn: TOÁN CHUYÊN Lớp: 11 ĐỀ CHÍNH THỨC
Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ CHÍNH THỨC MÔN: TOÁN CHUYÊN, LỚP: 11
(Bản hướng dẫn gồm 04 trang ) I. HƯỚNG DẪN CHUNG.
- Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số điểm từng
phần như Hướng dẫn quy định. Việc chi tiết hoá thang điểm (nếu có) so với thang điểm trong
Hướng dẫn phải đảm bảo không sai lệch với hướng dẫn chấm và được thống nhất thực hiện trong Tổ chấm.
- Tổng điểm của mỗi phần không làm tròn; tổng điểm của toàn bài được làm tròn đến 01 chữ số thập phân.
II. ĐÁP ÁN VÀ THANG ĐIỂM Câu ý Đáp án Điểm
Câu 1 (3.0 điểm). Tính các giới hạn sau: 1 4n x 2 a) 3 2 lim n n 3; b) lim ; c) lim ; n 1 4 3n x 2 2 x 5 3 5 n 2 2n 5 lim lim n 4n 3 3 n 4 0.5 n a) 1.0 5 2 n 1 lim 0.25 3 3.0 4 n Đ 1 0.25 2 n 1 3 2 1 2.3n n lim 3 lim 3n 2n 0.5 n 2n 3 1 3n b) 1.0 1 2 3n lim 0.25 2 n 1 3 2 0.25 Trang 2 x 1 2
x12 x12 lim lim 2 x 3 x 9 x3 2x 9 x12 x 3 0.5 lim x 3
x 3 x 3 x 1 2 c) 1.0 1 lim
x3 x 3 x 1 2 0.25 1 0.25 24
Tính đạo hàm của các hàm số sau: 5 2 1 2 x 2x 3 a) 4 3 y x x x ; b) y ; 4 3 10 x 1 c) 2 y x x 3 ; 5 4 2 3 1 5 3 2 2 y ' x x x ' .4.x .3.x 1 0.5 a) 1.0 4 3 10 4 3 3 2 5x 2x 1 0.5 2 x 2x 3 2 y x 1 x 1 x 1 2 2 (3.0 b) y ' 1 0.5 x 2 1 Đ) 1.0 2 x 2x 1 0.5 x 2 1 y x 2 x x 2 ' '. 3 . x 3' 2x 3 ' 2 1. x 3 . x 0.5 2 2 x 3 c) 1.0 2 2 x x 3 0.25 2 x 3 2 2x 3 0.25 2 x 3
Câu 3 (1.0 điểm). Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có
phương trình x 2 y 2 1 2 6 và điểm ( A 4;5) . Xác định 3 (1.0
phương trình đường tròn (C’) là ảnh của (C) qua phép tịnh tiến theo Đ) AO . AO =(4;5) 0.25 Trang 3
Đường tròn (C) có tâm I(1;2) bán kính R = 6
I’(x;y) là ảnh của I qua phép tịnh tiến AO II '= AO x 1 4 x 5 0.25 I’(5;7)
y 2 5 y 7
Đường tròn (C’) có tâm là I’ và bán kính là R’ = 6 . 0.25
(C’) có phương trình x 2 y 2 5 7 6 . 0.25 a S (1,0) H A D O B C Chỉ ra CD SA (vì SA (ABCD)) 0.5
CD AD (vì ABCD là hình vuông) CD (SAD) 4
Suy ra CD SD hay tam giác SCD vuông tại D. 0.25 1.5đ SD = 2 2 SA AD a 6 . 1 Kết luận 2 S S . D CD a 6 . SCD 2 0.25
Lập luận SA (ABCD) AC là hình chiếu. 0.25 b
(0,5) Chỉ ra góc cần tìm là góc nhọn SCA . Tính được AC = 2a 2 . 0.25 SA Suy ra 1 tan SCA hay 0 SCA 26 34'. AC 2 SA Suy ra 1 tan SCA hay 0 SCA 26 34'. AC 2 x 1 Cho hàm số y f (x)
có đồ thị (C). Viết phương trình tiếp tuyến x 2
của đồ thị (C) tại giao điểm của đồ thị (C) và trục hoành.
Gọi M là giao điểm của đồ thị (C) và trục hoành. Suy ra M 1 ;0 3 f '(x) 5 x 22 0.25 0.5 1 đ f '( 1 ) 3
Phương trình tiếp tuyến của đồ thị (C) tại M 1 ;0 là: y f ' 1 x 1 0 0.25 1 1 y x 3 3 6
Câu 6 (0.5 điểm). Học kì 1 năm học 2021-2022 lớp 11toan có tổng Trang 4 1.0đ
cộng 11 học sinh đạt giải trong các cuộc thi, trong đó: có 3 học sinh
giải nhất, 5 học sinh đạt giải nhì và 3 học sinh đạt giải ba. Giáo viên
chủ nhiệm chọn ngẫu nhiên 2 học sinh. Hỏi giáo viên chủ nhiệm có
bao nhiêu cách chọn để 2 học sinh đó có ít nhất một em đạt giải nhất.
Th1: cả 2 học sinh được chọn đều là giải nhất có 3 cách chọn 0.25
Th2: gồm 1 học sinh giải nhất và 1 học sinh không phải giải nhất có: 3.8=24 cách 0.25 Vậy có 27 cách
Câu 7 (0.5 điểm). Cho dãy số u xác định bởi công thức truy hồi n 1 u 1 2
, với n 1. Biết u có giới hạn hữu hạn khi n . n 1 u n 1 2 u n Tìm giới hạn đó. 1 2 3 4
Ta có u ,u ,u ,u 1 2 3 4 2 3 4 5 n Dự đoán * u ,n (2) n n 1
Chứng minh dự đoán trên bằng quy nạp: 1 - Với n = 1, u (đúng) 1 2 7 k 0.5đ
- Giả sử đẳng thức (2) đúng với n k,k 1 nghĩa là u . k k 1 0.25 k 1
- Cần chứng minh (2) đúng với n= k +1,tức là u k 1 k 2 1 1 k 1 Thật vậy: u . k 1 2 k u k k 2 2 k 1 n Vậy * u , n n n 1
Nếu học sinh bỏ qua phần chứng minh quy nạp mà giải đúng các bước
còn lại thì điểm tối đa là 0,25đ toàn bài n n 1 Từ đó ta có: limu lim lim lim 1 n n 1 1 1 0.25 n 1 1 n n
----------------- HẾT ----------------- Trang 5




