Đề ôn tập cuối kì 1 toán 11

ĐỀ MINH HỌA KIỂM TRA CUỐI KÌ 1
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. − Câu 1. x
Tập xác định của hàm số cos 2 y = là s inx +1    A. D = \ −
+ k2 | k   . B. D =
\ k2 | k  .  2  C. D =
\ k | k   . D. D = .
Câu 2. Tất cả các nghiệm của phương trình 3 sin x = là 2   x = +  k x = + k2  A. 3  (k ). 3 B.  (k ).  2  2 x = +  k x = + k2  3  3 x = + k2 
C. x = + k (k  ) . 3 D.  (k ) . 3 x = − + k2  3
Câu 3. Cho dãy số (a có * a = 2
− ; a = a + 2, n
. Công thức số hạng tổng quát của (a là n ) n ) 1 n 1 + n A. 2n − 4 B. n−2 C. 2n − 2 D. 2 − n + 4
Câu 4. Trong các dãy số (u ) có công thức số hạng tổng quát như sau, dãy số nào là cấp số nhân? n + n − A. n u = 3n −1. B. 4 2 u =
. C. u = 3.4n . D. ( 1) u = . n n n 5 n 3n +1 2025 Câu 5. Tính lim được kết quả bằng 2n + 3 2025 A. . B. 0 . C. 2025 . D. + . 2
Câu 8. Giá trị của giới hạn 2 lim x − 4 là x→ 2 A. 1. B. 2 − . C. 2. D. 3.
Câu 7. Cho hình chóp S.ABCD có đáy là hình vuông tâm O , M là trung điểm của SC . Mệnh đề nào sau đây sai?
A. OM (SAC) .
B. OM (SAB) .
C. OM (SAD) .
D. (SAB) (SAD) = SA.
Câu 8. Cho hình chóp S.ABC có M , N lần lượt là trung điểm của AB, BC . Gọi I là giao
điểm của AN và MC . Giao tuyến của hai mặt phẳng (SAN) và (SMC) là đường thẳng A. MN . B. SI . C. SB . D. SM .
Câu 9. Cho cấp số cộng (u với u = 3 và u = 7 . Giá trị của u bằng n ) 2 3 4 A.10. B. 4. C.15. D. 11.
Câu 10. Phương trình 2. o
c sx − 3 = 0 có tập nghiệm là  5   2 
A. S =  + k2 ;
+ k2 , k   .
B. S =  + k2 ;−
+ k2 , k   .  6 6   3 3     1 
C. S =  + k2 ;− + k2 , k   .
D. S =  + k2 , k   .  6 6  6 
Câu 11. Chiều cao của một số học sinh được thống kê trong bảng tần số ghép nhóm sau
Giá trị đại diện của nhóm 160;170) là A. 155. B. 165. C. 150. D. 55.
Câu 12: Khi thống kê chiều cao của học sinh khối 12 trong một trường trung học phổ thông, ta thu được
mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu ghép nhóm trên là
A. 150;156) .
B. 162;168) .
C. 168;174) . D. 180;186) .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai.  2 − x + 5  khi x  1 − Câu 1. Cho hàm số 2
f (x) = 2x − x − 3
. Các mệnh đề sau đúng hay sai?  2
x − 4x + m khi x  1 − 1
a) lim f (x) = − .
b) lim f (x) = 5 .
c) lim f (x) = . +  − + 3  x ( → − ) 1 x ( → − ) 1 0 2 x→   2  d) Biết rằng khi a m =
với a là phân số tối giản, b  0 thì hàm số f ( x) liên tục tại điểm x = 1 − . Khi đó b b 0
ta có a +b = 79. Câu 2.
Cho hình chóp S.ABCD , có đáy ABCD là một hình bình hành tâm O . Gọi I , K lần lượt là
trung điểm của SB và SD . Khi đó:
a) SO là giao tuyến của (SAC) và (SBD).
b) Giao điểm J của SA với (CKB) thuộc đường thẳng đi qua K và song song với DC .
c) Giao tuyến của (OI )
A và (SCD) là đường thẳng đi qua C và song song với SD .
d) CD // IJ .
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 4. u  = 1 −
Câu 1. Cho dãy số (u , biết 1 
với n 1. Tính u n ) u = u + 3  50 n 1 + n
Câu 2. Các bệnh truyền nhiễm có thể lây lan rất nhanh. Giả sử có tám người bị bệnh trong tuần đầu tiên
của một đợt dịch, và mỗi người bị bệnh sễ lây bệnh cho năm người vào cuối tuần tiếp theo. Tính
đến hết tuần thứ chín của đợt dịch, có bao nhiêu người đã bị lây bởi căn bệnh này?
Câu 3. Kết quả đo chiều cao ( theo đơn vị mét) của 81 cây keo lá tràm sau 5 năm tuổi ở một khu rừng
trồng được thống kê theo bảng sau. Chiều cao 1;5) 5;9) 9;13) 13;17) 17;2 )1 21;  25 Giá trị đại diện 3 7 11 15 19 23 Số cây 5 11 23 24 14 4
Giá trị  = Q − Q của mẫu số liệu ghép nhóm trên (làm tròn đến hàng đơn vị) Q 3 1
Câu 4. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm CD, N là trung điểm của đoạ SK
n AM . Mặt phẳng (P) đi qua N song song với mặt phẳng (SAB) cắt SC tại K . Tỉ số KC bằng bao nhiêu? PHẦN IV. Tự luận 
Câu 1. Giải phương trình 2sin(x + ) − 3 = 0 . 5
Câu 2. Một công ty tuyển một chuyên gia về công nghệ thông tin với mức lương năm đầu là 240 triệu
đồng và cam kết sẽ tăng thêm 5% lương mỗi năm so với năm liền trước đó. Tính tổng số lương mà chuyên
gia đó nhận được sau khi làm việc cho công ty 10 năm (làm tròn đến triệu đồng). 1 1 1 Câu 3. Cho u = + ... . Tính lim(3+ u n ) n 1.2 2.3 . n (n + ) 1
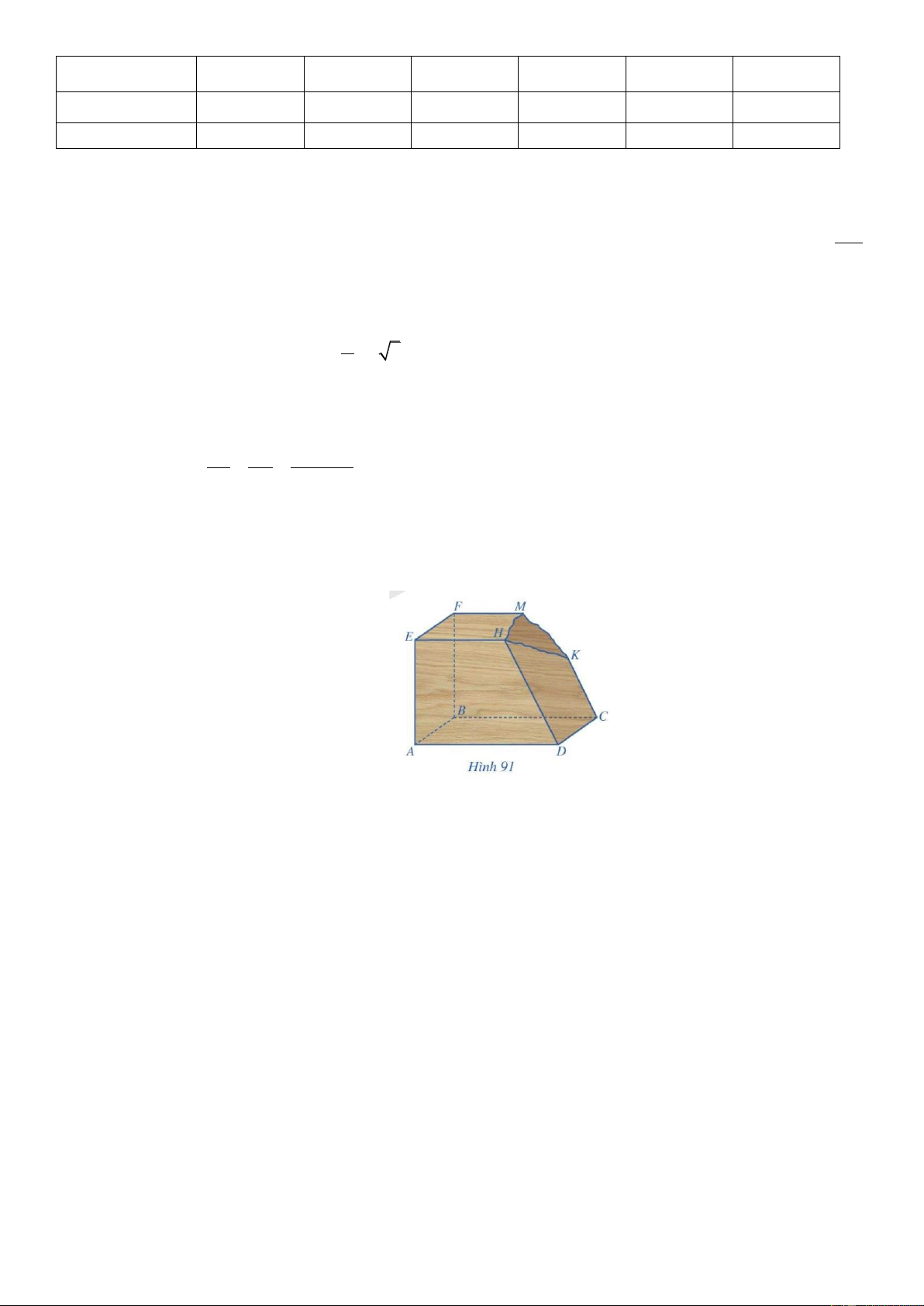
Câu 4. Một khối gỗ có các mặt đều là một phần của mặt phẳng với ( ABCD) / / (EFMH ),CK / /DH . Khối
gỗ bị hỏng một góc (Hình 91). Bác thợ mộc muốn làm đẹp khối gỗ bằng cách cắt khối gỗ theo mặt
phẳng (R) đi qua K và song song với mặt phẳng ( ABCD) .
Gọi I, J lần lượt là giao điểm DH , BF với mặt phẳng (R) . Biết BF = 70 cm, DH = 85 cm ,
CK = 50 cm . Tính FJ .