Đề học kì 1 Toán 9 năm 2023 – 2024 phòng GD&ĐT Nghĩa Hưng – Nam Định
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề khảo sát chất lượng cuối học kì 1 môn Toán 9 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Nghĩa Hưng, tỉnh Nam Định; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem.
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KÌ I NGHĨA HƯNG
NĂM HỌC 2023 – 2024
Môn: Toán – Lớp 9
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Phần 1- Trắc nghiệm khách quan (2 điểm):
Hãy chọn phương án đúng và viết chữ cái đứng trước phương án đó vào bài làm:
Câu 1: Điều kiện để biểu thức 3 - √1 − x có nghĩa là: A. x ≥ 1; B. x > 1; C. x ≤ 1; D. x < 1.
Câu 2: Biểu thức √327 − �11 − 6√2 có giá trị bằng: A. √2; B. - √2; C. 6 + √2; D. 6 - √2;
Câu 3: Giá trị của m để hai hàm số (x là biến số) y = (m – 1)x + 2 và y = mx – 1 cùng đồng biến trên R là: A. m > 1; B. m > 0; C. 0 < m < 1; D. m < 0.
Câu 4: Hoành độ giao điểm của đồ thị hai hàm số y = 2x – 3 và y = 3x – 2 là A. x = 1; B. x = - 1; C. x = 3 ; D. x = 2 2 3
Câu 5: Giá trị của m để đường thẳng y = (m – 2)x + m – 3 đi qua điểm A(2; - 1) là: A. m = - 2; B. m = 2; C. m = 3; D. m = - 3.
Câu 6: Cho ∆ABC vuông tại A, đường cao AH biết AH = 6cm, BH = 4cm. Khi đó độ dài đoạn thẳng HC bằng: A. 13cm; B. 10cm; C. 9cm; D. 3cm.
Câu 7: Cho ∆ABC vuông tại A biết AB = 2cm, ABC
� = 600. Bán kính đường tròn ngoại
tiếp ∆ABC có độ dài bằng A. 8cm; B. 4cm; C. 2cm; D. 1cm.
Câu 8: Cho đường tròn (O) có AB và AC là hai tiếp tuyến (B,C là tiếp điểm). Kết luận nào
sau đây “sai” ? A. ∆ABC cân tại A
B. AO là đường phân giác của BAC �
C. AO đi qua trung điểm của BC D. AB2 = AO2 + OB2
Phần 2. Tự luận (8 điểm). Câu 1. (2,0 điểm):
1, Tìm x, biết √4x − 8 + 3�x−2 = 6 9
2, Rút gọn các biểu thức a) 3 - 5− √5 - √20 ; √5−2 √5−1
b) �2√x + 1 � . x−√x với x ≥ 0; x ≠ 1 x−1 √x−1 3√x+1
Câu 2.(2,0 điểm): Cho hàm số y = 2x – 3
a) Vẽ đồ thị hàm số trên hệ trục toạ độ Oxy
b) Tìm m biết hàm số y = mx + m2 – m – 5 (x là biến số) đồng biến và đồ thị của nó cắt
đường thẳng y = 2x – 3 tại điểm có hoành độ bằng 1 2
Câu 3. (3 điểm): Cho đường tròn (O, R), đường kính BC, lấy điểm A trên đường tròn (O)
sao cho AB < AC. Vẽ OM ⊥ AC tại M
a) Tính OM nếu biết: R = 5cm; AC = 6cm
b) Tiếp tuyến tại C của đường tròn (O) cắt tia OM tại D. Chứng minh: DC2 = DM . DO
c) Gọi N là giao điểm của BD và đường tròn (O). Chứng minh: NBO � + NMO � = 1800 Câu 4.(1 điểm):
a) Giải phương trình: 3x2 + √𝑥𝑥2 + 1 = 1
b) Cho a ≥ 0, b ≥ 0, a2 + b2 ≤ 2.
Tìm giá trị lớn nhất của biểu thức: A = a�b(a + 2b) + b�a(b + 2a)
--------------Hết------------- 3 PHÒNG GD&ĐT HƯỚNG DẪN CHẤM NGHĨA HƯNG
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9
HỌC KÌ I - NĂM HỌC 2023 – 2024 Môn: Toán
Phần 1- Trắc nghiệm khách quan (2 điểm):
Mỗi câu lựa chọn đúng đáp án được 0,25 điểm Câu 1 2 3 4 5 6 7 8 Phương án đúng C A A B B C C D
Phần 2 - Tự luận (8 điểm):
Câu 1. (2 điểm): ĐK: x ≥ 2 = 6 1) √4x − 8 + 3�x−2 9 0,5điểm
⟺ 2√x − 2 + 3 √x − 2 = 6 3
⟺ 2√x − 2 + √x − 2 = 6 0,25 ⟺ 3√x − 2 = 6 ⟺ √x − 2 = 2 0,25 ⟺ x – 2 = 4 ⟺ x = 6 (tm). Kết luận 2a) 3 0,75
- 5− √5 - √20 = 3�√5+2� - √5�√5−1� - √4.5 √5−2 √5−1 5−4 √5−1 0,25 điểm
= 3�√5 + 2� − √5 − 2√5 0,25
= 3√5 + 6 − √5 − 2√5 = 6 0,25 2b) 0,75
với x ≥ 0; x ≠ 1 ta có �2√x + 1 � . x−√x x−1 3 điểm √x−1 √x+1 = � 2√x
+ 1 � . x−√x = 2√x+√𝑥𝑥+1 . x−√x �√x+1��√x−1� √x−1 3√x+1
�√x+1��√x−1� 3√x+1 0,25 = 3√x + 1 . √x�√x−1� �√x+1��√x−1� 3√x+1 0,25 = √x √x+1 0,25
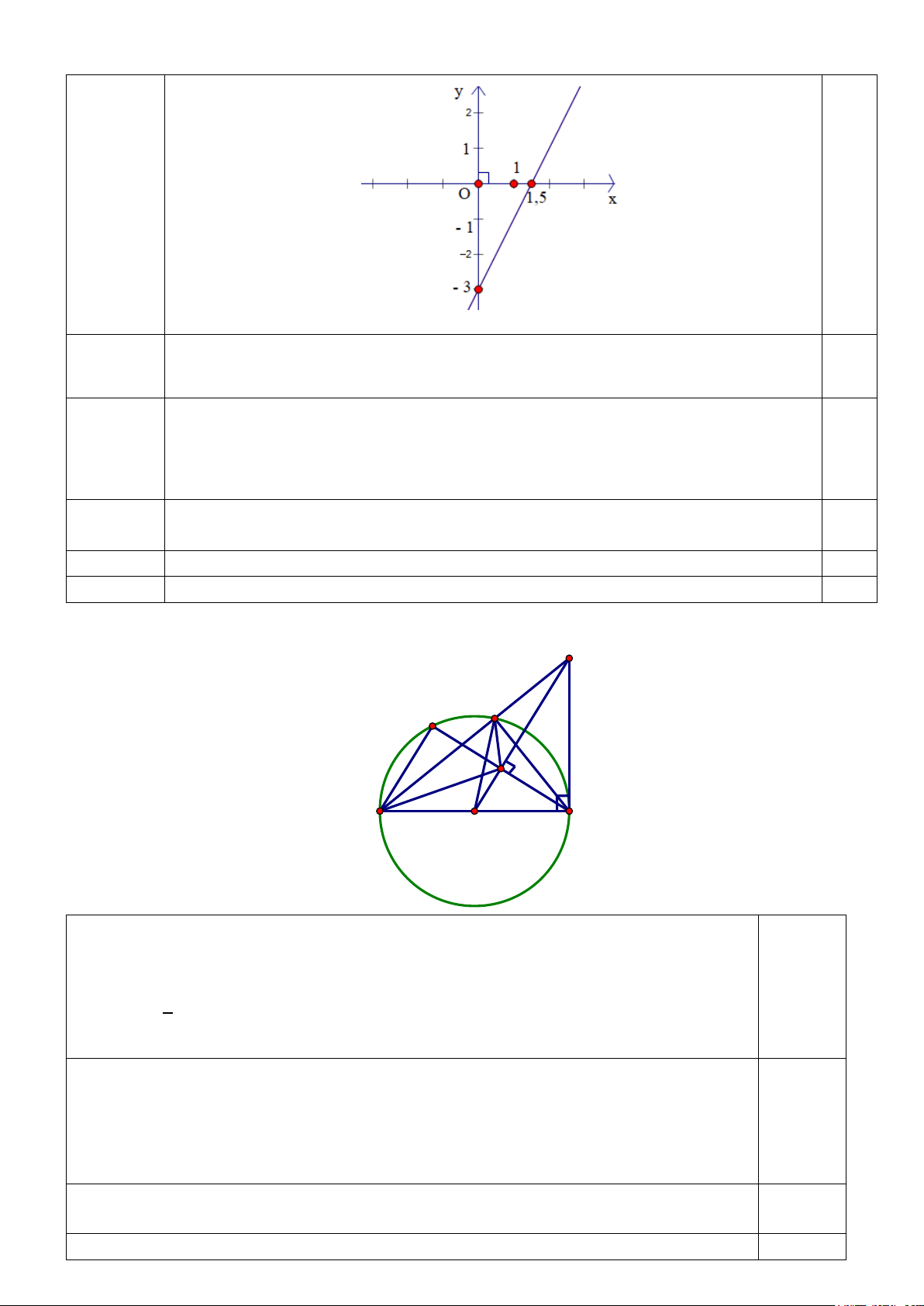
Câu 2. (2 điểm): a,
Cho x = 0 ⟹ y = - 3 ta có điểm (0; - 3) thuộc Oy
0,75điểm Cho y = 0 ⟹ x = 3 ta có điểm (3; 0) thuộc Ox 2 2 0,25
Đồ thị hàm số là đường thẳng đi qua hai điểm (0; - 3) và (3; 0) 2 4 0,5 b,
Thay x = 1 vào công thức y = 2x – 3 ta được y = 2.1 – 3 = - 1 1,25điểm 0,25
Ta có điểm (1; -1) có hoành độ bằng 1 thuộc đường thẳng y = 2x - 3
Đồ thị của hàm số y = mx + m2 – m – 5 cắt đường thẳng y = 2x – 3 tại
điểm của hoành độ bằng 1
⟹ Đồ thị của hàm số y = mx + m2 – m – 5 đi qua điểm (1; -1) 0,25 ⟹ x = 1; y = - 1
Thay x = 1; y = - 1 vào công thức y = mx + m2 – m – 5 ta được:
m. 1 + m2 – m – 5 = - 1 ⟺ m2 = 4 ⟺ m = 2; m = - 2 (*) 0,25
Mặt khác hàm số y = mx + m2 – m – 5 đồng biến nên m > 0 (**) 0,25
Từ (*) và (**)⟹ m = 2. KL 0,25 Câu 3.(3 điểm): D N A M B O C
Xét đường tròn (O), OM ⊥ AC (gt) 0,5đ
⟹ M là trung điểm của AC (Quan hệ vuông góc giữa đường kính và dây cung) ⟹ CM = 1 AC 2
Mà AC = 6cm (gt) nên CM = 3cm
Có OM ⊥ AC (gt) ⟹ ∆OCM vuông tại M
⇒ OC2 = OM2 + MC2 (Định lí Pitago)
Mà OC = 5cm (gt); MC = 3cm(cmt) 0,5đ Nên ta có 52 = OM2 + 32 ⇒ OM = 4(cm)
b) Xét đường tròn (O) có: CD là tiếp tuyến (gt) 0,25
⟹ CD ⊥ OC (....)⟹ ∆OCD vuông tại C (*)
OM ⊥ AC ⟹ CM là đường cao của ∆OCD (**) 0,25 5
Từ (*) và (**)⟹ CD2 = DM . DO 0,25
c, Xét đường tròn (O) có: ∆BCN nội tiếp đường tròn, cạnh BC là đường kính ⟹ ∆BCN vuông tại N 0,25 ⟹ CN ⊥ BD
⟹ CN là đường cao của ∆BCD (1)
CD ⊥ OC ⟹ ∆BCD vuông tại C (2)
Từ (1) và (2) ⟹ DN . DB = CD2 0,25
Mặt khác CD2 = DM . DO (cmt) ⟹ DN . DB = DM . DO 0,25
Chứng minh ∆DMN ∞ ∆DBO 0,25 ⟹ DMN � = DBO � Lại có DMN � + NMO � = 1800 0,25 ⟹ NBO � + NMO � = 1800 Câu 4.(1 điểm):
a) Giải phương trình: 3x2 + √𝑥𝑥2 + 1 = 1 Điều kiện: Mọi x ∈ R 3x2 + √𝑥𝑥2 + 1 = 1
⟺ 3(x2 + 1) + √𝑥𝑥2 + 1 = 4
Đặt √𝑥𝑥2 + 1 = t (t ≥ 1) phương trình trở thành 0,25
3t2 + t – 4 = 0 ⟺ t = 1 (tm t ≥ 1); t = 4 (tm t ≥ 1) 3
* t = 1 ta có: √𝑥𝑥2 + 1 = 1 ⟺ x = 0
* t = 4 ta có: √𝑥𝑥2 + 1 = 4 ⟺ x = √7; x = −√7 0,25 3 3 3 3 Kết luận
b) Cho a ≥ 0, b ≥ 0, a2 + b2 ≤ 2. Tìm GTLN của biểu thức A = a�b(a + 2b + b�a(b + 2a) Với a ≥ 0, b ≥ 0 ta có
A . √3 = a�3b(a + 2b + b�3a(b + 2a) 0,25
≤ a. 3b+(a+2b) + b. 3a+(b+2a) = a2+b2 + 5ab 2 2 2 ≤ a2+b2 + 5. a2+b2 ≤ 6 2 2 ⟹ A ≤ 2√3 0,25
Dấu “=” xảy ra khi và chỉ khi a = b = 1
Vậy GTLN của A bằng 2√3 khi a = b = 1
Document Outline
- Phần 1- Trắc nghiệm khách quan (2 điểm):