Đề học kì 2 Toán 7 năm 2023 – 2024 phòng GD&ĐT Vũ Thư – Thái Bình

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KÌ II HUYỆN VŨ THƯ Năm học 2023-2024 Môn: Toán 7 Đề chính thức
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM (3,0 điểm)
Chọn chữ cái đứng trước câu trả lời đúng trong mỗi câu sau:
Câu 1: Biết x và y là hai đại lượng tỉ lệ thuận và khi x = 2 thì y = - 4. Hệ số tỉ lệ a trong công thức y = ax là: A. - 2 B. - 8 C. 2 D. 6 Câu 2: Cho x y = và x - y = 3. Ta có: 3 2 A. x = - 9 ; y = - 6 B. x = 9 ; y = 6 C. x = 6 ; y = 9 D. x = 5 ; y = 6
Câu 3: Bảng sau cho biết kết quả xếp loại học tập của học sinh khối 7 của một trường THCS: Xếp loại Tốt Khá Đạt Chưa đạt Số học sinh 72 162 90 36
Tỉ lệ phần trăm học sinh đạt loại Tốt so với học sinh cả khối 7 là: A. 20% B. 16% C. 18% D. 14%
Câu 4: Một thùng kín đựng các quả bóng có cùng kích thước, trong đó có 20 quả bóng màu
đỏ và 20 quả bóng màu xanh. Lấy ngẫu nhiên một quả bóng trong thùng. Xác suất của biến
cố “Lấy được quả bóng màu xanh” bằng: A. 1 B. 1 C. 1 D. 1 3 2 20 40
Câu 5: Giá trị của đa thức 2
F(x) = x − 2x +1 tại x = - 1 là: A. 0 B. 1 C. 4 D. 5
Câu 6: Cho đa thức P(x) = ax2 + bx + c với a, b, c là các số thực. Biết đa thức P(x) chia hết
cho đa thức x - 1. Giá trị của biểu thức S = a + b + c là: A. S = 1 B. S = - 1 C . S = 0 D. S = 3
Câu 7: Trực tâm của một tam giác là giao điểm của ba đường nào? A. Ba đường trung trực.
B. Ba đường trung tuyến. C. Ba đường phân giác. D. Ba đường cao.
Câu 8: Cho ΔABC có AB < AC < BC. Ta có: A.  <   A B < C B.    C < B < A C.    B < A < C D.   <  B < C A
Câu 9: Cho ΔABC = ΔDEF. Biết  0 A = 60 ;  0 C = 40 . Số đo E là: A. 600 B. 400 C. 800 D. 1000
Câu 10: Cho ΔABC có trung tuyến AM và trọng tâm G. Ta có: Toán 7_ Trang 1 A. 1 AG = AM B. 2 GM = GA C. 1 GA = GM D. 1 GM = AM 3 3 3 3
Câu 11: Thể tích hình lập phương có cạnh dài 5 cm là: A. 25 cm3 B. 125 cm2 C. 125 cm3 D. 20 cm3
Câu 12: Số đỉnh của hình lăng trụ đứng tam giác là: A. 3 B. 4 C. 5 D. 6
PHẦN II: TỰ LUẬN (7,0 điểm)
Bài 1: (1,5 điểm) a) Tìm x biết x 3 − = . 6 4
b) Một hộp có 16 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, . . ., 15, 16.
Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất
của biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5”.
Bài 2: (2,5 điểm)
a) Thu gọn rồi tìm bậc, hệ số cao nhất, hệ số tự do của đa thức F(x) biết: ( ) 2 3 3 2
F x = 4x + 2 + 4x − 2x − 4x − x + 3x − 3.
b) Tìm đa thức H(x) = A(x) − B(x) biết: ( ) 4 3 A x = x + 4x + 3x − 2 và ( ) 4 3 B x = x − 2x + x +1.
c) Rút gọn rồi tìm nghiệm của đa thức M(x) = 3x(2x + ) 1 + (2 − x)(6x + 3).
Bài 3: (3,0 điểm)
Cho tam giác ABC cân tại A. Kẻ tia phân giác của  BAC cắt BC tại M.
a) Chứng minh ΔABM = ΔACM.
b) Qua M kẻ đường thẳng song song với AC cắt AB tại K. Chứng minh: KA = KM và K là trung điểm của AB.
c) Gọi H là giao điểm của AM và CK. BH cắt AC tại E. Chứng minh: AB + BC > 2BE.
_________________ Hết_________________
Họ và tên thí sinh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh . . . . . . . . . . . . . . . . . . . Toán 7_ Trang 2
ĐÁP ÁN BIỂU ĐIỂM
I.TRẮC NGHIỆM: (3,0 điểm) Mỗi phương án chọn đúng được 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A B A B C C D B C D C D
II. TỰ LUẬN: (7,0 điểm) Bài Nội dung Điểm Bài 1 a) Tìm x biết x 3 − = . (1,5 6 4
điểm) - Từ x 3 − = suy ra 4.x = - 3. 6 6 4 0,25 - Tìm được x = 9 − . 2 0,25
b) Một hộp có 16 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,
2, 3, . . ., 15, 16. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên
một thẻ trong hộp. Tính xác suất của biến cố “Số xuất hiện trên thẻ được rút
ra là số chia hết cho 5”.
- Số phần tử của tập hợp gồm các kết quả có thể xảy ra là 16
- Có ba kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số 0,5
chia hết cho 5” là: 5; 10; 15.
- Vậy xác suất của biến cố là 3 . 0,5 16
Bài 2 a) Thu gọn rồi tìm bậc, hệ số cao nhất, hệ số tự do của đa thức F(x) biết: (2,5 ( ) 2 3 3 2
F x = 4x + 2 + 4x − 2x − 4x − x + 3x − 3.
điểm) - Ta có F(x) = 4x2 + 2 + 4x3 - 2x - 4x3 - x2 + 3x - 3
= (4x3 - 4x3) + (4x2 - x2) + (3x - 2x) + (2 - 3) 0,25 = 3x2 + x - 1 0,25
Đa thức F(x) có: bậc là 2 ; hệ số cao nhất là 3; hệ số tự do là - 1. 0,25
b) Tìm đa thức H(x) = A(x) − B(x) biết: ( ) 4 3 A x = x + 4x + 3x − 2 và ( ) 4 3 B x = x − 2x + x +1. - Ta có H(x) = A(x) - B(x)
= (x4 + 4x3 + 3x - 2) - (x4 - 2x3 + x + 1) 0,25 Toán 7_ Trang 3
= x4 + 4x3 + 3x - 2 - x4 + 2x3 - x - 1 0,25 = 6x3 + 2x - 3 Vậy H(x) = 6x3 + 2x - 3. 0,25
(HS có thể đặt theo cột dọc để tính A(x) - B(x))
c) Rút gọn rồi tìm nghiệm của đa thức M(x) = 3x(2x + ) 1 + (2 − x)(6x + 3).
Ta có: M(x) = 3x( 2x + 1) + (2 - x)(6x + 3)
= 6x2 + 3x + 12x + 6 - 6x2 - 3x 0,5 = 12x + 6 0,25
- Tìm được nghiệm của đa thức M(x) là x = 1 − 2 0,25 Bài 3
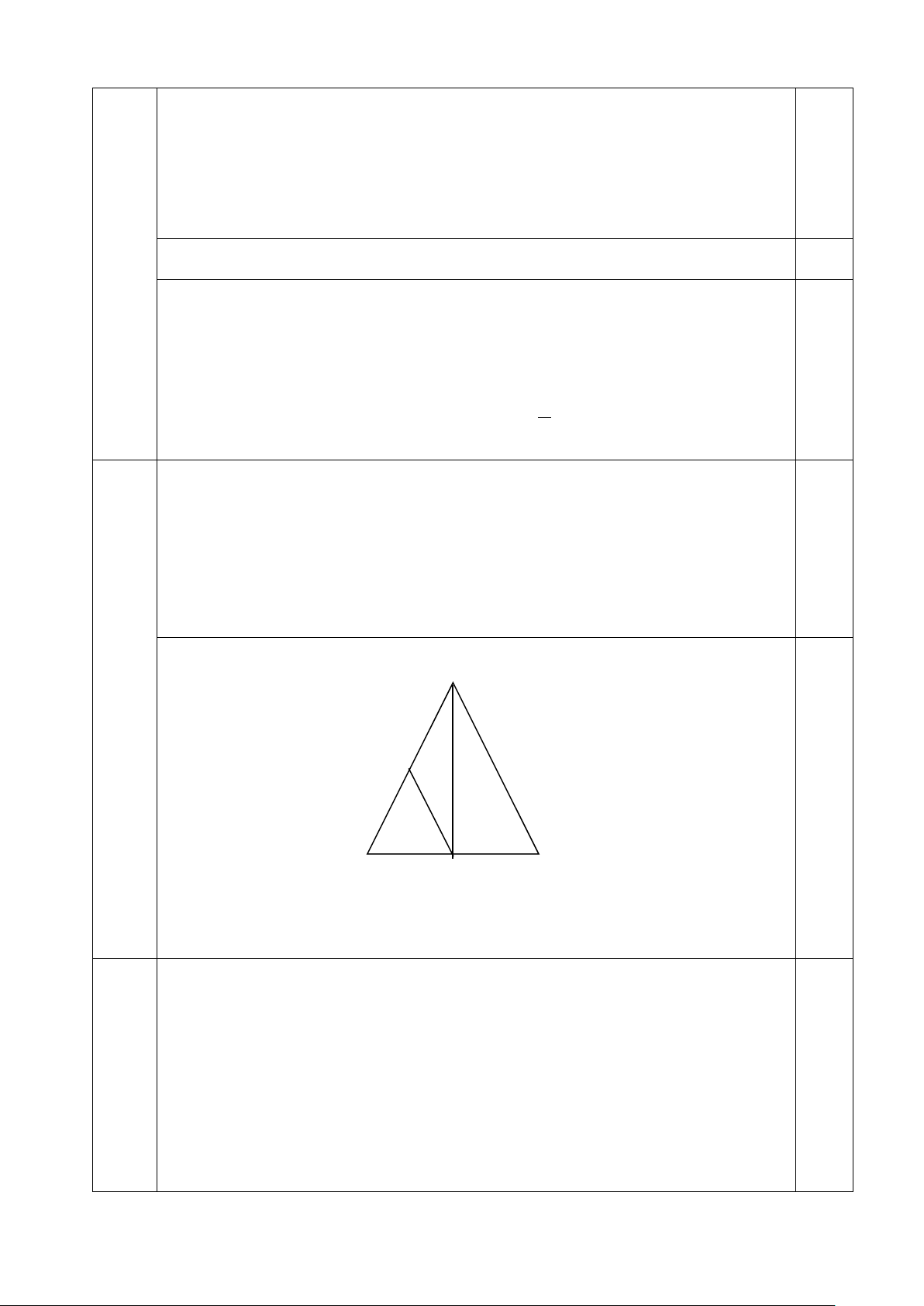
Cho tam giác ABC cân tại A. Kẻ tia phân giác của  BAC cắt BC tại M.
(3,0 a) Chứng minh ΔABM = ΔACM.
điểm) b) Qua M kẻ đường thẳng song song với AC cắt AB tại K. Chứng minh:
KA = KM và K là trung điểm của AB.
c) Gọi H là giao điểm của AM và CK. BH cắt AC tại E. Chứng minh: AB + BC > 2BE. A K B C M
- Vẽ hình đúng đến câu a. 0,25 a) Xét ΔABM và ΔACM có:
AB = AC ( hai cạnh bên của tam giác cân ABC) 0,5  BAM = 
CAM ( vì AM là phân giác của  BAC ) AM chung.
Suy ra ΔABM = ΔACM ( c.g.c) 0,25 Toán 7_ Trang 4 b) * Vì KM // AC suy ra  KMA =  CAM ( so le trong) 0,25  CAM = 
BAM ( vì AM là phân giác của  BAC ) Suy ra  KMA =  BAM 0,25 ⇒ AKM ∆ cân tại K ⇒ KA = KM. 0,25 * Vì KM // AC suy ra  KMB=  ACB ( đồng vị) 0,25 Mà  ACB= 
ABC ( hai góc ở đáy của tam giác cân ABC) suy ra  KMB=  ABC ⇒ BK ∆ M cân tại K. ⇒ KB = KM. 0,25
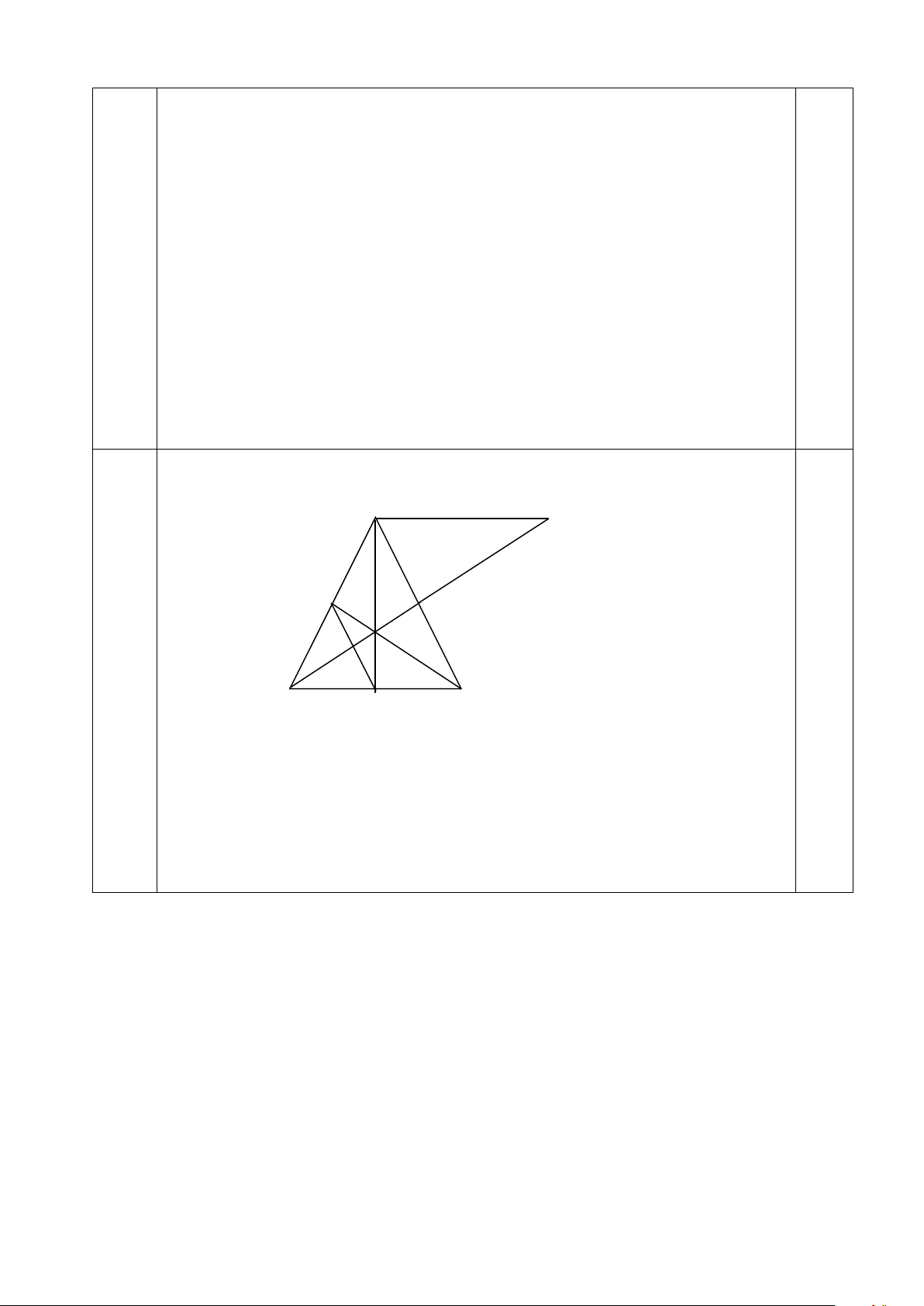
Mà KM = KA suy ra KA = KB ⇒ K là trung điểm của AB. 0,25 c) A F K H E B C M
- Trên tia BE lấy F sao cho E là trung điểm của BF. - Chứng minh BC = AF. 0,25
Áp dụng bất đẳng thức tam giác cho tam giác ABF có AB + AF > BF Suy ra AB + BC > 2BE. 0,25
Lưu ý: - Học sinh giải cách khác đúng vẫn cho điểm tối đa.
- Điểm bài khảo sát làm tròn đến 1 chữ số thập phân sau dấu phẩy. Toán 7_ Trang 5