Đề học kỳ 1 Toán 8 năm 2022 – 2023 trường THCS Đông Ninh – Thanh Hóa
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề thi khảo sát chất lượng cuối học kỳ 1 môn Toán 8 năm học 2022 – 2023 trường THCS Đông Ninh, tỉnh Thanh Hóa; đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm.
Preview text:
PHÒNG GD&ĐT ĐÔNG SƠN
BÀI THI KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I
TRƯỜNG THCS ĐÔNG NINH
NĂM HỌC: 2022 - 2023
Môn: Toán – Lớp 8 (Thời gian làm bài 90 phút)
Họ và tên học sinh: ……………………………………………………………………………… Lớp: 8……….. Số báo danh Giám thị 1 Giám thị 2 Số phách Điểm Giám khảo 1 Giám khảo 2 Số phách ĐỀ BÀI
Bài 1: (1,5 điểm) Phân tích các đa thức sau thành nhân tử:
a) 4x2 + 6xy b) x2.(x - 3) + 4.(3 - x)
Bài 2. (2,5 điểm)
1. Chứng tỏ rằng biểu thức sau không phụ thuộc vào giá trị của biến: 2 2
M (x 2)(x 2x 4) x(x 1) x
2. Cho đa thức A = 2x3 - 6x2 + 2x + a và đa thức B = x - 2. 1
a) Tính giá trị của đa thức B khi x 2
b) Tìm a để A chia hết cho B 2 2 2 x 1
Bài 3. (2,0 điểm) Cho A :
x 2, x 1) 2 2
2 x x 4 x x 2x (với
a) Rút gọn biểu thức A.
b) Tìm giá trị nguyên của x để A nhận giá trị nguyên.
Bài 4. (3,0 điểm)
Cho tam giác ABC vuông tại A (ABa) Tứ giác AMNC là hình gì? Vì sao?
b) Trên tia đối của tia MN lấy điểm D sao cho MN = MD. Chứng minh tứ giác
ADBN là hình thoi. Tính diện tích hình thoi ADBN, biết AB = 6cm, AC = 8cm.
c) Gọi E, F lần lượt là trung điểm của MN, AC. Chứng minh B, E, F thẳng hàng.
Bài 5. (1 điểm) Tìm tất cả các cặp số nguyên (x ; y) thoả mãn: 2 2
x y 3 x . y Bài làm
........................................................................................................................................................................................................................................................
........................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................
........................................................................................................................................................................................................................................................
........................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................
........................................................................................................................................................................................................................................................
........................................................................................................................................................................................................................................................
...................................................................................................................................................................................................................................................
ĐÁP ÁN VÀ BIỂU ĐIỂM ĐỀ HỌC KÌ 1 TOÁN 8 năm 2022 - 2023 Bài Phần Nội dung Điểm 2 a)
4x 6xy 2x(2x 3y) 0,75 Bài 1 2 2 b) x .x
3 4.3 x x .x 3 4.x 2
3 (x 3)(x 4) (x 3)(x 2)(x 2) 0,75 2 2
M (x 2)(x 2x 4) x(x 1) x 1đ 3 3 1.
M x 8 x x x M 8 V
ậy giá trị biểu thức M không phu thuộc giá trị của biến.
a) Thay x = -1/2 vào B ta được B = -1/2 – 2 = -5/2 0,5
b) Xét: 2x3 - 6x2 + 2x + a x - 2 2x3- 4x2 2x2 - 2x - 2 Bài 2: -2x2 + 2x + a 2.5 đ -2x2 + 4x 1.0 - 2x + a 1.5 - 2x + 4 a - 4
Để đa thức 2x3 - 6x2 + 2x + a chia hết cho đa thức x - 2 thì đa thức dư
phải bằng 0 nên => a - 4 = 0 => a = 4
Cách 2: Đặt f(x) = 2x3 - 6x2 + 2x + a chia hết cho đa thức x – 2 thì
f(2) = 0 2.23 – 6.22 + 2.2 + a = 0 - 4 + a = 0 a = 4. 2 2 2 x 1 A : 2 2
2 x x 4 x x 2x 2 2 2 x 1 A :
2 x (x 2)(x 2) x x(x 2) a 2(x 2) 2 2(x 2) x 1 A : Bài 3:
(x 2)(x 2) (x 2)(x 2) x(x 2) x(x 2) 2x 4 2
2x 4 x 1 A :
(x 2)(x 2) x(x 2) 2x 6 x 3 A :
(x 2)(x 2) x(x 2)
Để P thuộc Z thì x 2 1 Z
Z x 11; 1 x 2; 0 b x 1 x 1
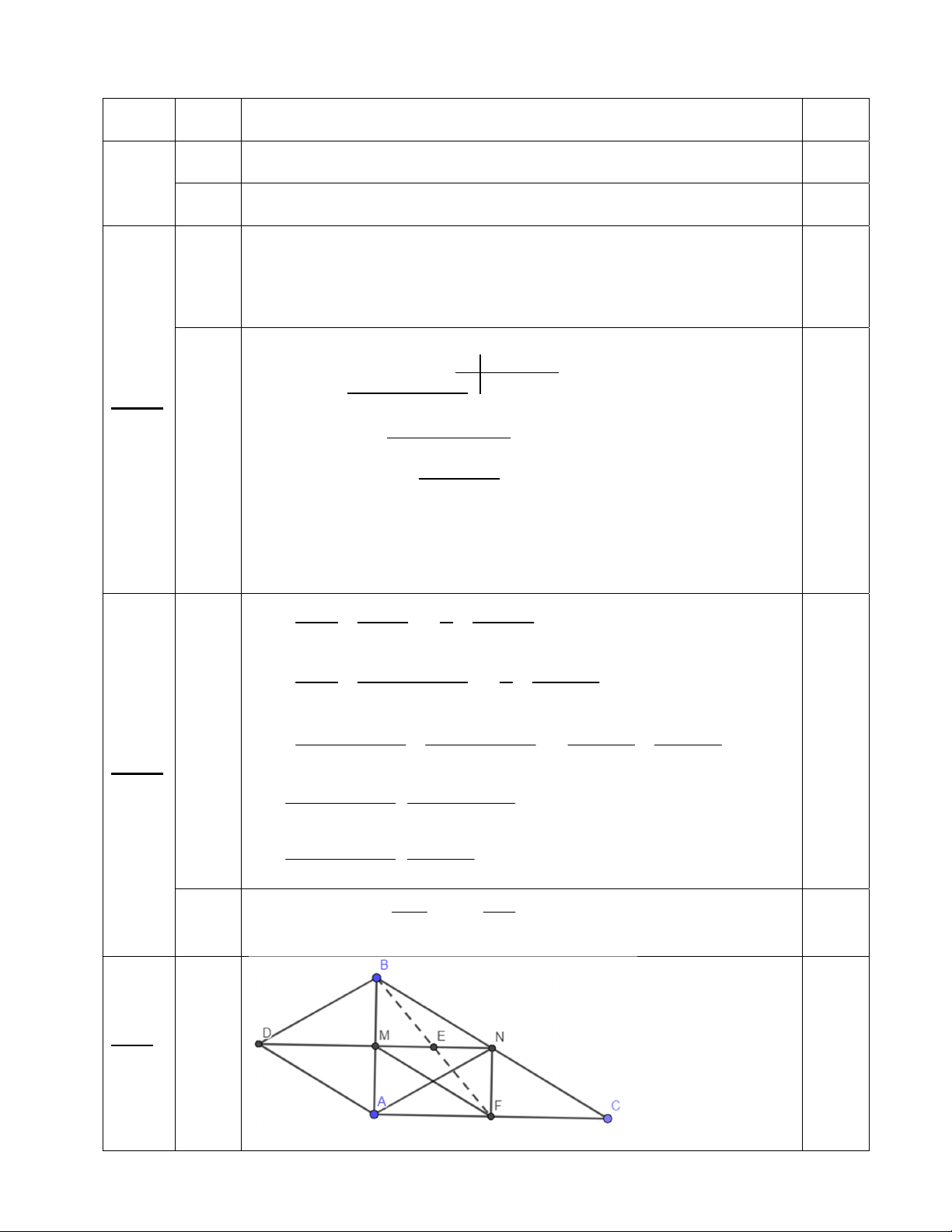
Kết hợp đkxđ ta được x = 0. 0.5đ Bài 4 3đ HS vã hình và gt – kl
a) Tứ giác AMNC là hình gì? Vì sao? 1đ
Chứng minh MN là đường trung bình của tg ABC AMNC là hình thang Mà góc A = 900
AMNC là hình thang vuông
b) Chứng minh tứ giác ADBN là hình thoi 0.75đ
M là trung điểm của AB và DN
ADBN là hình bình hành Mà AB vuông góc với DN ADBN là hình thoi
+) Có MN = 1/2AC = 4cm, DN = 2 MN = 2.4 = 8cm. 0.25đ
Diện tích hình thoi ADBN là:
SADBN = ½.AB . DN = ½.6.8 = 24 (cm2)
c) Chứng minh B, E, F thẳng hàng. 0.5đ
Chứng minh tg BMFN là hình bình hành Mà E là trung điểm MN
=> E là trung điểm BF => B, E, F thẳng hàng 2 2 2 2
x y 3 xy 2x 2y 6 2xy 1đ 2 2 2 2
(x y 2xy) 6(x y ) 2 2 2
(x y) 6(x y ) (*) Câu 5 Vì 2
(x y) 0 ,
x y nên từ (*) suy ra 2 2 2 2
6 (x y ) 0 x y 6 2 0 x 6 2 x 0;1; 4 x 0; 1 ; 2 Thay vào (*) Ta được (x, y) ( 2 ;1);(1; 2 );(2; 1 );( 1 ;2);(1;1 ) Chú ý:
- Các cách làm khác nếu đúng vẫn cho điểm tối đa, điểm thành phần giám khảo tự phân
chia trên cơ sở tham khảo điểm thành phần của đáp án.
- Đối với bài (Hình học): Không vẽ hình, hoặc vẽ hình sai cơ bản thì không chấm.
- Các trường hợp khác tổ chấm thống nhất phương án chấm.