Đề thi học kì 1 Toán 8 Cánh diều
I. TRẮC NGHIỆM KHÁCH QUAN: (3,0 điểm)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1 : Kết quả thu gọn của A= (2x2-4xy+5)+(3xy-5) A. 2x2-x2y2 B.2x2-7xy C.2x2-xy D.2x2-xy+10
Câu 2 : Thương của phép chia (12x4y + 4x3 – 8x2y2) : (4x2) bằng B. 3x4y + x3– 2x2y2 B. -12x2y + 4x – 2y2 C. 3x2y + x – 2y2 D. -3x2y + x – 2y2
x  4x  4
Câu 3. Kết quả rút gọn phân thức là x  4
A. x  4
B. x  4
C.  x  2 4
D.  x  2 4 x  x 
Câu 4: Thực hiện phép tính 3 12 2 8 . ta được 4x 16 x  4 3 3 3 3  A. B. C. D. 2 2  x  4 2 2  x  4
Câu 5. Cho h m số y = f(x) = 2x2 - 1. Khẳng định n o sau đây đúng? A. f(-1) = -3. B. f(1) = 1. C. f(-1) = -1. D. f(1) = 3.
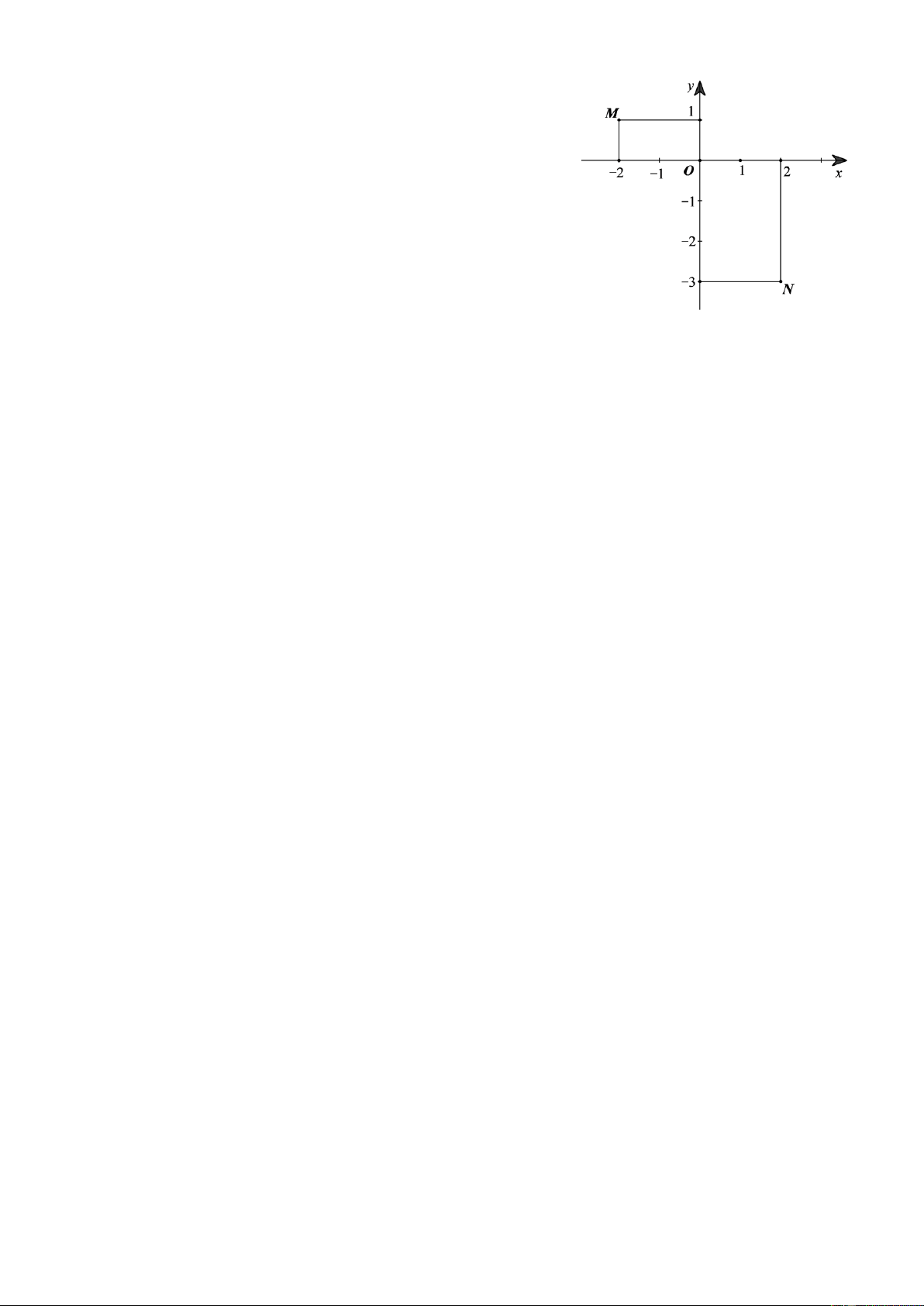
Câu 6. Cho điểm A v B trong mặt phẳng tọa độ Oxy như
hình bên. Khẳng định n o sau đây đúng? A. N (-3; 2). B. N(2; -3). C. M (1; -2). D. M (-1; 2).
Câu 7. Cho hai đường thẳng d: y = ax + b (a ≠ 0) v d': y = a'x + b' (a' ≠ 0). Với điều kiện n o sau
đây thì hai đường thẳng d v d' song song? A. a = a'. B. a = a' và b = b'. C. a ≠ a'. D. a = a' v b ≠ b'.
Câu 8. Góc tạo bởi đường thẳng y = -2x + 1 với trục Ox A. góc nhọn. B. góc vuông. C. góc tù. D. góc bẹt.
Câu 9. T ng số cạnh bên v cạnh đ y của một hình chóp tứ gi c đều A. 4. B. 6. C. 8. D. 10.
Câu 10 : Hình chóp tam gi c đều có cạnh đ y 20dm, chiều cao mặt bên 10dm, có diện tích xung quanh là: A. 100 dm3 B. 100 dm2 C. 300 dm3 D. 300 dm2
Câu 11. Một hình thang vuông có một góc bằng 75° góc còn ại không vuông của hình thang đó có số đo A. 25°. B. 75°. C. 105°. D. 125°.
Câu 12. Hình thoi cần thêm yếu tố n o để trở th nh hình vuông?
A. Hai đường chéo vuông góc.
B. Hai đường chéo bằng nhau.
C. Hai cạnh kề bằng nhau.
D. Một đường chéo tia phân gi c của một góc.
II. TỰ LUẬN : (7,0 điểm)
Câu 1. (1 điểm) Rút gọn c c biểu thức sau 2
a)  x  2 – 3  x x – 3 1 1 2x b)   2 x  5 x  5 x  25
Câu 2. (1 điểm) Phân tích đa thức th nh nhân tử
a) 5x  x  2  3x  6 b) 2 2
x  2xy  y 1 Câu 3. (1 điểm)
a) Bạn Đ o dự định gấp một hộp qu hình chóp tứ gi c đều có cạnh đ y
bằng 6cm v chiều cao 4cm, để đựng món qu tặng sinh nhật bạn Nam.
(xem hình ảnh minh họa). Thể tích tối đa m hộp qu có thể chứa được bao nhiêu?
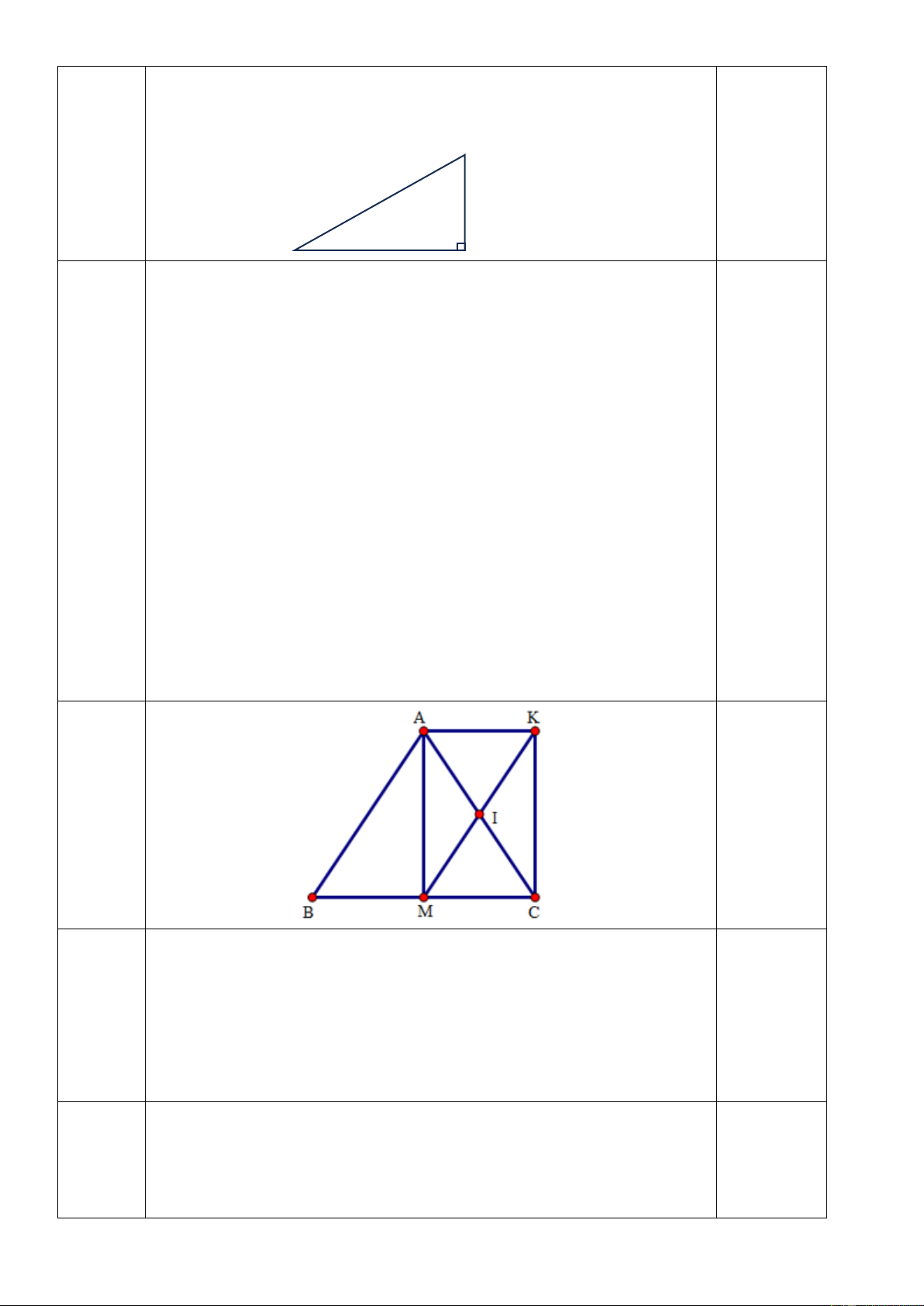
b) Một bạn học sinh thả diều ngo i đồng, cho biết đoạn dây
diều từ tay bạn đến diều d i 50m v bạn đứng c ch nơi diều
được thả ên theo phương thẳng đứng 25m. Tính độ cao của
con diều so với mặt đất, biết tay bạn học sinh c ch mặt đất 1m.
(kết quả làm tròn đến phần mười.)
Câu 4. (1 điểm) H m chi phí đơn giản nhất h m chi phí bậc
nhất y = ax + b, trong đó b biểu thị chi phí cố định của hoạt động kinh doanh v hệ số a biểu thị
chi phí của mỗi mặt h ng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố
định hằng ng y 36 triệu đồng v mỗi chiếc xe đạp có chi phí sản xuất 1,8 triệu đồng.
a) Viết công thức của h m số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ng y.
b) Có thể sản xuất bao nhiêu chiếc xe đạp trong ng y, nếu chi phí trong ng y đó 72 triệu đồng?
Câu 5: (2,5 điểm) Cho A
 BC cân tại A có đường trung tuyến AM, gọi I trung điểm của AC.
Lấy điểm K sao cho I trung điểm của đoạn thẳng MK.
a) Chứng minh tứ gi c AMCK hình chữ nhật
b) Tứ gi c AKMB hình gì? Vì sao?
c) Tìm điều kiện của tam gi c ABC để tứ gi c AMCK hình vuông.
Câu 6. (0,5đ) Cho biểu thức 2
A  x  6x  11. Tính gi trị nhỏ nhất của biểu thức . A
..................HẾT................
I. TRẮC NGHIỆM (0,25 điểm/câu) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C C B B C B D C C D C B II. TỰ LUẬN Câu Đáp án Điểm a)
x  22 – 3  xx 3 2 2      x 4x 4 (x 9) 0,25đ 2 2  x  4x  4  x  9 0,25đ  4x 13 b) 1 1 2x   2 x  5 x  5 x  25 x  5 x  5 1 2x     0,25đ
x  5 x  5  x  5 x  5  x  5 x  5
x  5  x  5  2x  
x  5 x  5 2x 10   0,25đ
x  5 x  5 x  x  5 x   
x  5 x  5 x  5
Câu 2. (1 điểm) Phân tích đa thức th nh nhân tử
a) 5x  x  2  3x  6 0,25đ =5x(x-2)+3(x-2) 0,25đ =(x-2)(5x+3) 2 2 2
x  2xy  y 1 2
b)   x  y 2 1 0,25đ
 x  y  
1  x  y   1 0,25đ
a) Thể tích của hộp qu : 1 0,5đ 3 .6.6.4  48 (m ) 3
b) Áp dụng định ý Pytago v o tam gi c vuông ABC, có: 2 2 2   0,25đ 3 BC AB AC 2 2 2 2 2 
AC  BC  AB  50  25  1875
 AB  1875  25 3  43,3
Vậy độ cao con diều so với mặt đất là 43,3 + 1 = 44,3m 0,25đ
(Bài làm học sinh không có hình và đặt tên thì không chấm) C B A
a) Công thức của h m số bậc nhất biểu thị chi phí y (triệu đồng) để
sản xuất x (xe đạp) trong một ng y : 0,5đ
y = 1,8x + 36 (triệu đồng).
b) Do chi phí trong ng y đó 72 triệu đồng nên y = 72 (triệu đồng).
Thay y = 72 v o công thức y = 1,8x + 36 ta có: 4 1,8x + 36 = 72 1,8x = 36 0,5đ x = 20
Vậy với chi phí 72 triệu đồng thì trong ng y đó có thể sản xuất
được 20 chiếc xe đạp. 5
a) ΔABC cân tại A có AM đường trung tuyến
=> AM đường cao => AMC  90 0,25đ Xét tứ gi c AMCK có: I trung điểm AC (gt)
I trung điểm MK (K điểm đối xứng với M qua I)
=> AMCK là hình bình hành 0,5đ Lại có 0,25đ
AMC  90 => AMCK là hình chữ nhật
b) Ta có: AK//MC (AKCM là hcn), BMC => AK//BM (1) 0,25đ
Lại có: AK=MC (AKCM hcn), BM=MC (M trung điểm của AC) 0,5đ =>AK=BM(2)
Từ (1) v (2)=> AKMB hình bình h nh 0,25đ
c) Hcn AMCK là hình vuông  AM=MC  AM=1/2BC
 ∆ABC vuông tại A (theo tính chất đường trung tuyến ứng với 0,25đ
cạnh huyền trong tam gi c vuông) M ∆ABC cân tại A (gt)
Vậy để AMCK hình vuông thì ∆ABC vuông cân tại A 0,25đ 2
A  x  6x 11 2 2 2
A  (x  2.3x  3 )  3 11 2     6 A (x 3) 2 2 voi moi x 0,25đ
Dấu “ = ’’ xảy ra khi x – 3 = 0  x  3
Vậy GTNN của A = 2 khi x = 3 0,25đ