Đề học kỳ 1 Toán 9 năm 2023 – 2024 phòng GD&ĐT Hải Hậu – Nam Định

PHÒNG GD&ĐT HẢI HẬU
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I NĂM HỌC 2023 - 2024 Môn: Toán lớp 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
(Đề khảo sát gồm 02 trang)
I. PHẦN TRẮC NGHIỆM (2 điểm)
Hãy chọn phương án trả lời đúng và ghi chữ cái đứng trước phương án đó vào bài làm.
Câu 1. Căn bậc hai số học của 25 là A. 5. B. 5 ± . C. – 5 D. 5 .
Câu 2. Biểu thức −x +1 xác định khi và chỉ khi 2024
A. x ≥1. B. x >1. C. x <1. D. x ≤1.
Câu 3. Tất cả các giá trị của x thỏa mãn 3 x ≤ 2 là A. x ≤ 8 . B. 0 ≤ x ≤ 8 . C. x ≥ 8 . D. 0 ≤ x ≤ 4.
Câu 4. Hàm số y = (k + )2
2 x + 2023(k là tham số) luôn đồng biến trên R khi và chỉ khi A. k > 2 − . B. k ≠ 2 − . C. k < 2 − . D. k > 0.
Câu 5. Tọa độ giao điểm của hai đường thẳng y = x + 5 và y = 2x + 3là A. (7;2) . B. ( 2; − 3) . C. (2;7) . D. (3; 2 − ) . Câu 6. Cho sin 2 α = thì tanα bằng 2 A. 1 . B. 1. C. 3 . D. 2 . 2 2
Câu 7. Số lượng đường tròn bàng tiếp của một tam giác là A. 0. B. 1. C. 2. D. 3.
Câu 8. Đường thẳng a cách tâm O của đường tròn (O; 3cm) một khoảng bằng 8 cm. Số giao điểm
của đường thẳng a và đường tròn (O; 3cm) là A. 0. B. 1. C. 2. D. 3.
II. PHẦN TỰ LUẬN (8 điểm)
Bài 1 (2,0 điểm):
1) Rút gọn các biểu thức sau: a) A = − − ( − )2 2 48 75 1 3 3 .  −  b) x x 2 3 =  −  : − x B  (với 0 ≤ x ≠ ) 9 . x + 3 x 9  − x − 6 x +   9
2) Phân tích thành nhân tử x + 3 x + 2 − 2 (với x ≥ 2 − )
Bài 2 (2,0 điểm): Cho hàm số y = mx – 4 (m là tham số, m khác 0) (1).
1) Vẽ đồ thị hàm số (1) với m = 1.
2) Xác định tất cả các giá trị của m để đồ thị hàm số (1) trùng với đồ thị hàm số y = 2x – m2.
3) Xác định tất cả các giá trị của m để đồ thị hàm số (1) cắt đường thẳng y = -3x + 2 tại điểm có tung độ bằng 5.
Bài 3 (3,0 điểm):
1) Để hái buồng cau trên một cây cau thẳng đứng so với mặt đất,
người ta dùng một chiếc thang tre thẳng có chiều dài từ nấc thang trên
cùng (là thanh ngang tiếp xúc trực tiếp với thân cây cau) đến chân thang
tre là 5m. Tính số đo góc nhọn tạo bởi thang tre và cây cau, biết chiều
cao từ mặt đất lên tới vị trí đặt nấc thang trên cùng của thang tre là 4,5m
và mặt đất là một mặt phẳng. (Kết quả số đo góc làm tròn đến phút).
2) Cho nửa đường tròn (O) đường kính AB, tiếp tuyến Bx tại B (Bx và nửa đường tròn thuộc cùng
một nửa mặt phẳng bờ là AB). Qua điểm C trên nửa đường tròn (O) (C khác A, B) kẻ tiếp tuyến với
nửa đường tròn cắt Bx ở M, tia AC cắt Bx ở D. a) Chứng minh: MB = MC và 2
AB = AC.AD .
b) Kẻ CH ⊥ AB (H∈AB), gọi I là trung điểm CH. Chứng minh: M là trung điểm của BD và ba
điểm A, I, M thẳng hàng.
Bài 4 (1,0 điểm): 1) Giải phương trình 2
18 − 3x − x + 8 = 2 3− x + 4 x + 6.
2) Cho x, y, z là các số thực dương thoả mãn 1 1 1 + +
= 1. Tìm giá trị lớn nhất của biểu
1+ x 1+ y 1+ z thức 1 1 1 P = + + . xy yz zx
----------Hết---------
PHÒNG GD&ĐT HẢI HẬU
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I
NĂM HỌC 2023 – 2024 Môn: Toán lớp 9
I. PHẦN TRẮC NGHIỆM (2 điểm)
Mỗi câu trả lời đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 Đáp án A D A B C B D C
II. PHẦN TỰ LUẬN (8 điểm) Bài Ý
Nội dung trình bày Điểm a) A = − − ( − )2 2 48 75
1 3 3 = 2.4 3 - 5 3 - 1− 3 3 0,5 = 3 3 − (3 3 −1)= 1 0,25  −  b) x x 2 3 =  −  : − x B  (với 0 ≤ x ≠ ) 9 . x + 3 x 9  − x − 6 x +   9   1 x x − 2 3   = − : − x 0,25 (1,5đ)  x + 3 
( x +3)( x −3) (3− x)2 1
x ( x −3)− x + 2 1 = : (2,0 đ) ( 0,25
x + 3)( x −3) 3− x 3 − x + 2 3 x − 2 = ( − x = . x 0,25 + 3)( x −3).(3 ) x+3
x + 3 x + 2 − 2 (với x ≥ 2 − ) = ( x + )2
2 + 4 x + 2 − x + 2 − 4 0,25 2
(0,5đ) = x + 2( x + 2 + 4) −( x + 2 + 4) 0,25
= ( x + 2 + 4)( x + 2 − )1
Vẽ đồ thị hàm số y = mx – 4 với m = 1
Với m = 1 ta có hàm số y = x - 4 0,25 1
(0,75đ) Xác định đúng tọa độ hai điểm A(0; -4), B(4; 0) thuộc đồ thị của hàm số.
Đồ thị hàm số là đường thẳng AB. 0,25 Vẽ đồ thị 0,25
Xác định giá trị của m để đồ thị hàm số (1) trùng với đồ thị hàm số y = 2x – m2. m = 2 2 2
Đồ thị hàm số (1) trùng với đồ thị hàm số y = 2x – m2 ⇔  0,25 2 (2,0 đ)  4 − = −m (0,5đ ) m = 2 ⇔ 
⇔ m = 2 (thỏa mãn m ≠ 0). Kết luận………….. 0,25 m = 2 ±
Xác định giá trị của m để đồ thị hàm số (1) cắt đường thẳng y = -3x +2 tại điểm có tung độ bằng 5. 3
(0,75 Đồ thị hàm số (1) cắt đường thẳng y = -3x +2 ⇔ m ≠ -3
đ) Theo đề bài thì đường thẳng y = -3x +2 đi qua điểm có tung độ bằng 5 nên với y = 5 0,25 thì 5 = -3.x + 2 ⇔ x = -1
Do đó đồ thị hàm số (1) cắt đường thẳng y = -3x +2 tại điểm có tung độ bằng 5. 0,25
⇔ Đồ thị hàm số (1) đi qua điểm có tọa độ (-1; 5)
⇔ 5 = m.(-1) - 4 ⇔ m = - 9 (thỏa mãn m ≠ -3, m ≠ 0). KL……… 0,25
1) Để hái buồng cau trên một cây cau thẳng đứng so với mặt đất, người ta dùng một
chiếc thang tre thẳng có chiều dài từ nấc thang (thanh ngang) trên cùng đến chân
thang tre là 5m. Tính số đo góc tạo bởi thang tre và cây cau (Góc tạo bởi từ nấc thang
trên cùng về phía gốc cau và chân thang), biết chiều cao từ mặt đất lên tới vị trí đặt 1
nấc thang trên cùng của thang tre là 4,5m và mặt đất là một mặt phẳng. (Kết quả số
(1,0 đo góc làm tròn đến phút).
đ) Giả sử ∆ ABC vuông tại A có BC = 5m, AC = 4,5m. 0,25 Khi đó  AC 4,5 CosACB = = = 0,9 0,25 BC 5 ⇒  0 ACB ≈ 25 51' 0,25 Kết luận………….. 0,25
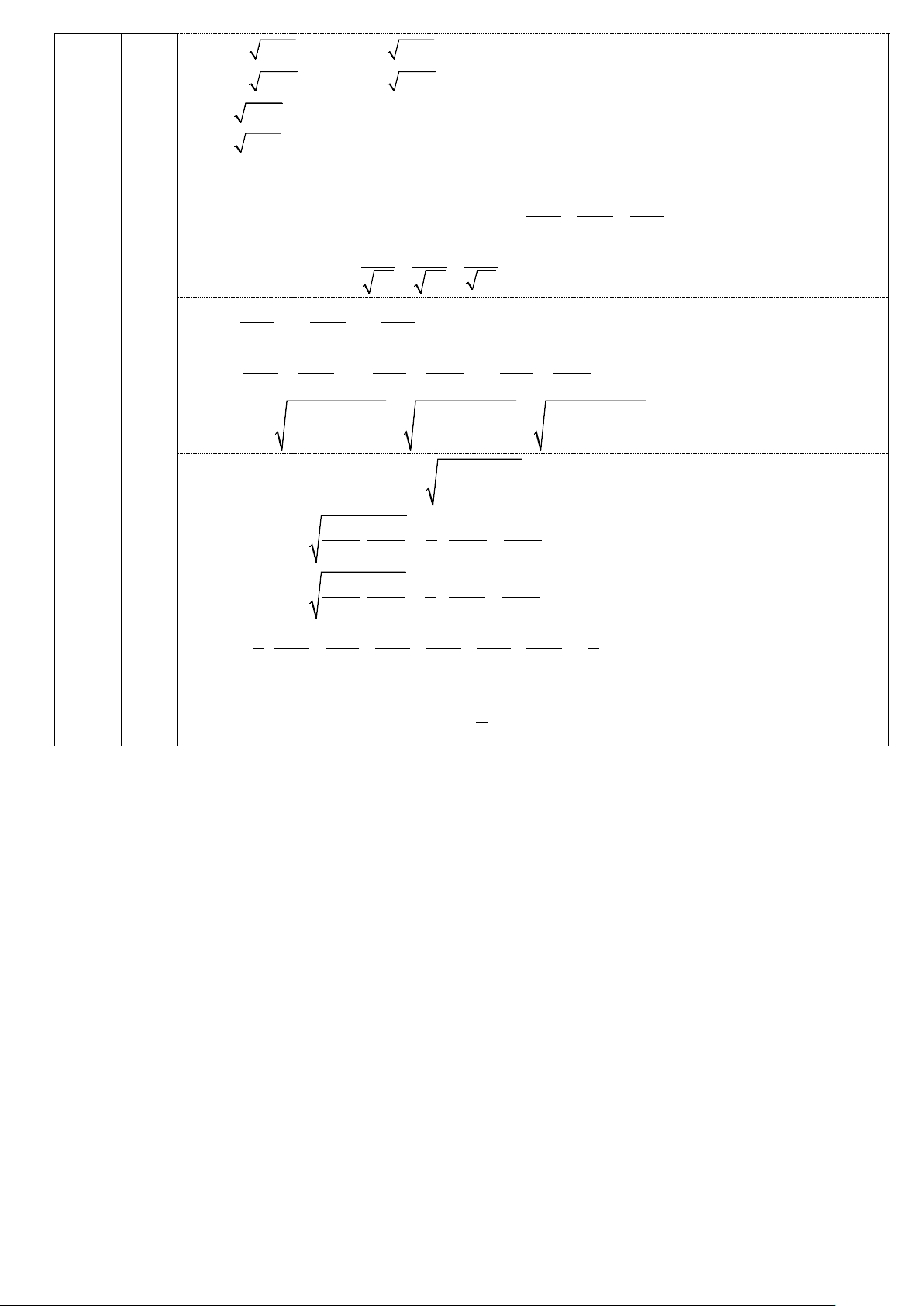
2) Cho nửa đường tròn (O) đường kính AB, tiếp tuyến Bx tại B (Bx và nửa đường
tròn thuộc cùng một nửa mặt phẳng bờ là AB). Qua điểm C trên nửa đường tròn (O)
(C khác A, B) kẻ tiếp tuyến với nửa đường tròn cắt Bx ở M, tia AC cắt Bx ở D. a) Chứng minh: MB = MC và 2
AB = AC.AD .
b) Kẻ CH ⊥ AB (H∈AB), gọi I là trung điểm CH. Chứng minh: M là trung điểm
của BD và ba điểm A, I, M thẳng hàng. D C M 3 I (3,0 đ) A O B H 2 (2,0
đ) a) +) Vì MC, MB là hai tiếp tuyến cắt nhau tại M của đường (O) (B, C là các tiếp điểm) nên MC = MB (đpcm) 0,25
+) Chứng minh ∆ ABD vuông tại B
Chứng minh ∆ ACB vuông tại C ⇒ BC ⊥ AD tại C. 0,5
Xét ∆ ABD vuông tại B có BC ⊥ AD tại C nên 2
AB = AC.AD (đpcm) 0,25
b) +) Chứng minh ∆ BCD vuông tại C ⇒  +  CBD CDB = 900(1) 0,25 Chứng minh  +  DCM MCB = 900 (2)
Vì MC = MB (3) nên ∆ MCB cân tại M ⇒  MCB = 
MBC (4) nên từ (1), (2), (4) ⇒  = 
MCD CDB ⇒ MC = MD (5). 0,25
Từ (3), (5) ⇒ MB = MD ⇒ M là trung điểm của BD +) Chứng minh CH // DB. ' '
Gọi I’ là giao điểm của AM và CH. Chứng minh I H I C  AI  = = 0,25 MB MD  AM   
Mà MB = MD nên I’H = I’C hay I’ là trung điểm của CH.
Lại có I là trung điểm của CH nên I trùng I’ mà A, I’, M thẳng hàng nên A, I, M 0,25 cũng thẳng hàng (đpcm). Giải phương trình 2
18 − 3x − x + 8 = 2 3− x + 4 x + 6 4) 1
⇔ (3− x)(x + 6) +8 − 2 3− x − 4 x + 6 = 0 − ≤ x ≤ ) (1,0 đ) (0,5đ (ĐKXĐ: 6 3 0,25 )
⇔ ( 3− x − 4)( x + 6 − 2) = 0  3− x − 4 = 0  3− x = 4 ⇔  ⇔   x + 6 − 2 = 0  x + 6 = 2
+) x + 6 = 2 ⇔ x + 6 = 4 ⇔ x = 2 − (Thỏa mãn) 0,25
+) 3− x = 4 ⇔ 3− x =16 ⇔ x = 13 − (Loại)
Vậy tập nghiệm của phương trình là S = {− } 2
2) Cho x, y, z là các số thực dương thoả mãn 1 1 1 + + = 1. Tìm giá trị lớn
1+ x 1+ y 1+ z nhất của biểu thức 1 1 1 P = + + . xy yz zx Ta đặt 1 1 1 = a, = b,
= c (ĐK: a,b,c > 0 ). Khi đó a + b + c = 1 1+ x 1+ y 1+ z 1− a b + c 1− b a + c 1 ⇒ = = , = = , − c a + b x y z = = a a b b c c 0,25 Do đó ab bc ca P = + + 2
(b + c)(c + a)
(c + a)(a + b)
(a + b)(b + c) (0,5đ a b  a b  )
Theo bất đẳng thức Cauchy có: 1 . ≤ +  ;
b + c c + a 2  a + c b + c  b c 1 .  b c  ≤ +  ;
c + a a + b 2  b + a c + a  c a 1 .  c a  ≤ +  .
a + b b + c 2 0,25
 c + b a + b  Nên 1  a b b c c a  3 P ≤ + + + + + =
2  a c b c b a c a c b a b  + + + + + +  2
Dấu “=” xảy ra ⇔ x = y = z = 2
Vậy giá trị lớn nhất của biểu thức P là 3 tại x = y = z = 2 . 2
Chú ý: Nếu học sinh làm theo cách khác nếu đúng vẫn cho điểm tương đương.