Đề học kỳ 2 Toán 7 năm 2023 – 2024 phòng GD&ĐT Hai Bà Trưng – Hà Nội

UBND QUẬN HAI BÀ TRƯNG
ĐỀ KIỂM TRA HỌC KỲ II
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học 2023 - 2024 MÔN: TOÁN 7 ĐỀ CHÍNH THỨC Ngày kiểm tra: 06/05/2024
Thời gian làm bài: 90 phút
I/ Trắc nghiệm: (2,0 điểm)
Câu 1: Cho đa thức A(x) = - 2x3 + 4x + 5. Hệ số cao nhất của A(x) là: A. - 2 B. 5 C. 3 D. Đáp án khác
Câu 2: Biểu thức đại số nào sau đây biểu thị chu vi hình chữ nhật có chiều dài bằng 7(cm) và chiều rộng bằng x (cm) A. 7x B. 7 + x. C. (7 + x).2 D. (7 + x): 2.
Câu 3: Kết quả quả thu gọn của đa thức 2 2
5x  4x  3  4x  4x  3 là: A. 2 9x 8x B. 2 x 8x C. 2 x  6 D. 2 9x 8x  6
Câu 4: Giá trị x  4 là nghiệm của đa thức nào sau đây ?
A. Px  x2 4 B. H x  4x 10
C.Q x  2x 8 D. Ax 162x
Câu 5: Biến cố “Khi gieo đồng xu thì được mặt ngửa” là: A. Biến cố không thể C. Biến cố ngẫu nhiên B. Biến cố chắc chắn
D. Các đáp án trên đều đúng
Câu 6: Trong các hình sau, đâu là hình lăng trụ đứng tam giác ? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Câu 7: Trong một tam giác, trực tâm là giao điểm của ba đường nào ? A. Đường phân giác; C. Đường trung trực; B. Đường trung tuyến; D. Đường cao.
Câu 8: Cho ABC và MHK có AB = MH,  A = 
M . Cần thêm một điều kiện gì để ABC bằng
MHK theo trường hợp cạnh – góc – cạnh ? A. BC = MK B. BC = HK C. AC = MK D. AC = HK
II/ Tự luận: (8,0 điểm)
Bài 1: (1,5 điểm) Cho đa thức A(x) = - 5x4 + 3x3 + 2x2 – 2x3 – 4x2 + 1 và B(x) = 5x4 + 2x2 - 28
a) Thu gọn và sắp xếp đa thức A(x) theo lũy thừa giảm dần của biến. b) Tính B(2)
c) Tìm nghiệm của A(x) + B(x) Bài 2: (1,5 điểm).
a) Tìm x, biết: x(x + 1) – x2 + 15 = 0
b) Chứng minh giá trị của đa thức P(x) = (x + 1)(x – 2) – x(x + 2) + 3x không phụ thuộc biến.
c) Thực hiện phép tính:  4 3
6x  4x  3x  2: (3x  2)
Bài 3: (1,0 điểm) Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số tự nhiên
từ 1 đến 10. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.
a) Liệt kê các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút. Có bao nhiêu
kết quả có thể xảy ra.
b) Tính xác suất của biến cố: “Số xuất hiện trên thẻ được rút ra là số chẵn”.
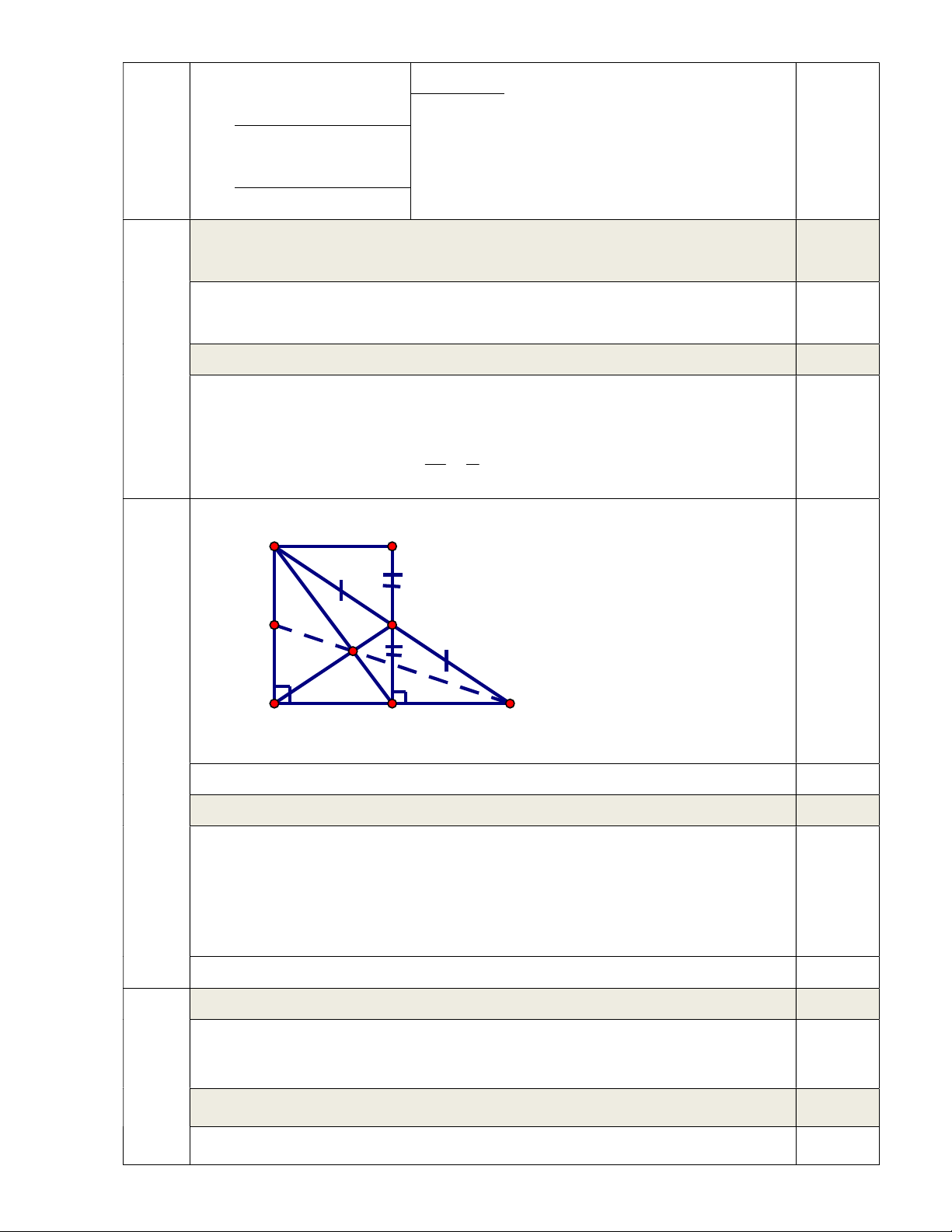
Bài 4: (3,5 điểm) Cho ∆ABC vuông tại A, vẽ đường trung tuyến AM (M ∈ BC). Từ M kẻ MH
vuông góc với AC (H ∈ AC), trên tia đối của tia MH lấy điểm K sao cho MK = MH.
a) Chứng minh: ∆MHC = ∆MKB. b) Chứng minh: BK // HC. c) Chứng minh:  KBH =  BHA và BK = AH
d) Gọi G là giao điểm của BH và AM, I là trung điểm của AB.
Chứng minh: ba điểm I, G, C thẳng hàng.
Bài 5: (0,5 điểm) Tính giá trị biểu thức:
C = x14 − 10x13 + 10x12 − 10x11 + ⋯ + 10x2 − 10x + 10 tại x = 9.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD: . . . . . . . . . . . . . . UBND QUẬN HAI BÀ TRƯNG
HD CHẤM KIỂM TRA HỌC KỲ II
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học 2023 – 2024 MÔN: TOÁN 7
I/ Trắc nghiệm: (2 điểm) Mỗi câu trả lời đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 Đáp án A C B C C A D C II/ Tự luận: (8 điểm): Bài Nội dung Điểm
Cho đa thức A(x) = - 5x4 + 3x3 + 2x2 – 2x3 – 4x2 + 1 và B(x) = 5x4 + 2x2 - 28 0,5
a) Thu gọn và sắp xếp đa thức A(x) theo lũy thừa giảm dần của biến.
A(x) = - 5x4 + 3x3 + 2x2 – 2x3 – 4x2 + 1 0,25
A(x) = - 5x4 + (3x3 – 2x3) + (2x2 – 4x2) + 1 = - 5x4 + x3 – 2x2 + 1 0,25 b) Tính B(2) 0,5 1 B(2) = 5.24 + 2.22 – 28 0,25 (1,5đ) = 80 + 8 – 28 = 60 0,25
c) Tìm nghiệm của A(x) + B(x) 0,5
A(x) + B(x) = - 5x4 + x3 – 2x2 + 1 + 5x4 + 2x2 – 28 0,25
= - 5x4 + 5x4 + x3 – 2x2 + 2x2 + 1 – 28 = x3 – 27 x3 – 27 = 0  x = 3 0,25
a) Tìm x: x(x + 1) – x2 + 15 = 0 0,5đ a) x(x + 1) – x2 + 15 = 0 x2 + x – x2 + 15 = 0 0,25 x2 – x2 + x + 15 = 0 x + 15 = 0 x = - 15 0,25 2
b) Chứng minh giá trị của đa thức P(x) = (x + 1)(x – 2) – x(x + 2) + 3x không 0,5 (1,5đ) phụ thuộc biến. P  x 2 2
 x  x  2x  2  x  2x  3x 0,25 P  x  2 0,25
Vậy giá trị của đa thức P(x) không phụ thuộc biến
c) Thực hiện phép tính:  4 2
6x  4x  3x  2:(3x  2) 0,5đ 6x4 – 4x3 + 3x - 2 3x – 2 - 6x4 – 4x3 2x3 + 1 3x - 2 - 3x – 2 0
a) Liệt kê các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút. 0,5
Có bao nhiêu kết quả có thể xảy ra.
Các kết quả có thể xảy ra: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10 0,25
Có 10 kết quả có thể xảy ra 0,25 3
b) Tính xác suất của biến cố: “Số xuất hiện trên thẻ được rút ra là số chẵn”. 0,5 (1đ)
Có 4 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số 0,25 chẵn” là: 2; 4; 6; 8; 10 5 1 0,25
Xác suất của biến cố là:  10 2 B K M I G C 4 A H 0,25 (3,5đ)
Vẽ đúng hình đến hết câu a HS ghi đầy đủ GT; KL 0,25
a) Chứng minh: ∆MHC = ∆MKB. 0,75 Xét ∆MHC và ∆MKB. MH = MK (gt)  0,5 HMC =  KMB (đối đỉnh)
MC = MB (AM là trung tuyến trong ABC) ⇒ ∆MHC = ∆MKB (c.g.c) 0,25 b) Chứng minh: BK // HC 0,75 Vì ∆MHC = ∆MKB   KBM = 
HCM (cặp góc tương ứng) 0,25
Mà chúng ở vị trí so le trong  BK // HC 0,5 c) Chứng minh:  KBH =  BHA và BKH = HAB 1 BK // HC  BK // AH   KBH =  BHA (so le trong) 0,25 ∆MHC = ∆MKB (cmt)    0 BKH = KHC  90 0,25
Xét ABH vuông tại A và KHB vuông tại K: BH chung  0,25 
 ABH = KHB (ch-gn) KBH =  BHAcmt
Do đó, BK = AH (2 cạnh tương ứng) 0,25
d) Chứng minh: ba điểm I, G, C thẳng hàng. 0,5
MHC = MKB  BK = CH (cặp cạnh tương ứng) 0,25
Mà BK = AH (cmt)  HC = HA ⇒ BH là đường trung tuyến của ∆ABC
Mà AM là đường trung tuyến của ∆ABC ⇒ G là trọng tâm của ∆ABC 0,25
Mà CI là trung tuyến của ∆ABC ⇒ I, G, C thẳng hàng
Tính giá trị biểu thức: 0,5
C = x14 − 10x13 + 10x12 − 10x11 + ⋯ + 10x2 − 10x + 10 tại x = 9.
C = x14 − 10x13 + 10x12 − 10x11 + ⋯ + 10x2 − 10x + 10 tại x = 9. 5 Thay x = 9 vào đa thức 0,25 (0,5đ) 14 13 12 11 2
C  9 10.9 10.9 10.9 10.9 10.9 10 14 C  9  9   13 1 .9  9   12 1 .9  9   11 1 9  9   2 1 .9  9   1 .9 10 C   14 14   13 13    2 2 9 9 9 9 9  9   9 10 0,25 C  1
Lưu ý: - Điểm toàn bài để lẻ đến 0,25.
- Học sinh giải cách khác đúng cho điểm tối đa.