


Preview text:
UBND HUYỆN NHO QUAN
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
Năm học 2013 – 2014 MÔN: TOÁN 6
ĐỀ THI CHÍNH THỨC
(Thời gian làm bài 120 phút)
Đề thi gồm 05 câu, trong 01 trang Câu
1(6 điểm). Tính:
a, 150 - (100 - 99 + 98 - 97 + … - 3 + 2 - 1) 2 2 2 b, 3 5 7 8 8 8 3 5 7 c, 2 3 199 200 1 3 3 ... 3 3 2013 2013 2013 2013 ... d, 2 3 4 2014 2013 2012 2011 1 ... 1 2 3 2013
Câu 2(3,5 điểm). 1. So sánh: 66 55 và 55 66 2.
Chứng tỏ rằng: Nếu 9x 5y chia hết cho 17 thì 2x 3y chia hết cho 17.
Câu 3(4 điểm). 1. Tìm x,
biết: a, 15 - (-53 + x) = 95 b, 15 4 17 3x 2 3 4
2. Tìm số tự nhiên n để A = 15 có giá trị lớn nhất. n 9
Câu 4(4 điểm).
1. Cho góc xOz và góc zOy là hai góc kề bù. Biết góc zOy bằng bốn lần góc xOz.
a) Tính số đo góc xOz và góc zOy.
b) Gọi Om là tia phân giác của góc zOy. Tính số đo góc xOm.
2. Cho 2015 đường thẳng. Trong đó hai đường thẳng bất kỳ nào cũng cắt
nhau và không có ba đường thẳng nào cùng đi qua một điểm. Tính số giao điểm của chúng. Câu
5(2,5 điểm).
1. Tìm hai số tự nhiên a,b. Biết 5a = 4b và BCNN(a,b) = 140
2. Cho a, b là hai số nguyên tố cùng nhau. Chứng minh rằng 8a 3b là phân 5a 2b số tối giản. Hết
Họ và tên thí sinh…………………………………Số báo danh…………………………...
Giám thị 1:……………………………………Giám thị 2:………………………………… UBND HUYỆN NHO QUAN HƯỚNG DẪN CHẤM PHÒNG GD&ĐT
KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
NĂM HỌC 2013 – 2014
Môn toán - Lớp 6 Câu ý Nội dung Điểm 1
150 - (100 - 99 + 98 - 97 + … - 3 + 2 - 1)
(6,0) a = 150 100 99 98 97 ... 2 1 0,5
(1,5đ) = 150 - (1 + 1 + 1…+ 1) (50 số 1) 0,5 = 150 - 50 0,25 = 100 0,25 b 2 2 2 1 1 1 (1,5đ) 2 3 5 7 3 5 7 = 1,0 8 8 8 1 1 1 8 3 5 7 3 5 7 = 1 4 0,5 c 2 3 199 200 1 3 3 ... 3 3
(1,5đ) Đặt: M = 1 +3 + 32+ +…+ 3199 + 3200
Ta có: 3M = 3.(1 +3 + 32+ +…+ 3199 + 3200 ) 0,5 = 3 + 32 +…+ 3200 + 3201
3M- M =(3 + 32 +…+ 3200 + 3201 ) - (1 +3 + 32+ +…+ 3199 + 3200 ) 0,5 2M = 3201 – 1 201 3 1 0,5 M 2 d 2013 2013 2013 2013 (1,5đ) ... 2 3 4 2014 2013 2012 2011 1 ... 1 2 3 2013 1 1 1 1 2013 ... 2 3 4 2014 2012 2011 1 1 1 ... 1 1 0,5 2 3 2013 1 1 1 2013 ... 2 3 2014 2014 2014 2014 0,5 ... 1 2 3 2013 1 1 1 2013 ... 2 3 2014 1 1 1 0,25 2014 ... 2 3 2014 2013 2014 0,25 2 1 So sánh: 66 55 và 55 66
(3,5) (2,0đ) Ta có: 5566 = (11.5)66 = 1166.566 =1166.(56)11 =1166.1562511 0,5
6655 = (11.6)55 = 1155.655 =1155.(65)11 =1155.777611 0,5 Mà 1166 > 1155 1562511 > 777611
Nên 1166.1562511 > 1155.777611 0,75 Vậy 66 55 > 55 66 0,25
2 Ta có: 9x 5y 1 7
(1,5đ) 4.9x 5y 1 7
36x 20y 1 7 0,5
34x 17y 2x 3y 17
172x y 2x 3y 1 7 0,5
Mà: 172x y 1 7 2x 3y 1 7
Vậy nếu 9x 5y chia hết cho 17 thì 2x 3y chia hết cho 17. 0,5 3 1a 15 - (-53 + x) = 95 (4,0) (1,0đ) 53 x 15 95 0,25 53 x 80 0,25 x 80 53 x 27 0,25 Vậy x = - 27 0,25 1b 15 4 17 3x (1,5đ) 2 3 4 4 15 17 3x 0,25 3 2 4 4 13 3x 0,25 3 4 4 13 0,25 3x 3 4 +) 4 13 3x +) 4 13 3x 3 4 3 4 13 4 13 4 3x 3x 4 3 4 3 23 55 3x 3x 12 12 23 55 x x 36 36 0,5 Vậy 23 55 x ; 0,25 36 36 2
(1,5đ) Ta có: 15 > 0 và không đổi. 0,25 0,5
Nên A = 15 có giá trị lớn nhất khi n - 9 > 0 và có giá trị nhỏ nhất (1) 0,25 n 9 0,25
Ta lại có: n N n 9 Z (2)
Từ (1) và (2), suy ra n - 9 =1 0,25 n = 10
Vậy với n = 10 thì thỏa mãn đầu bài.
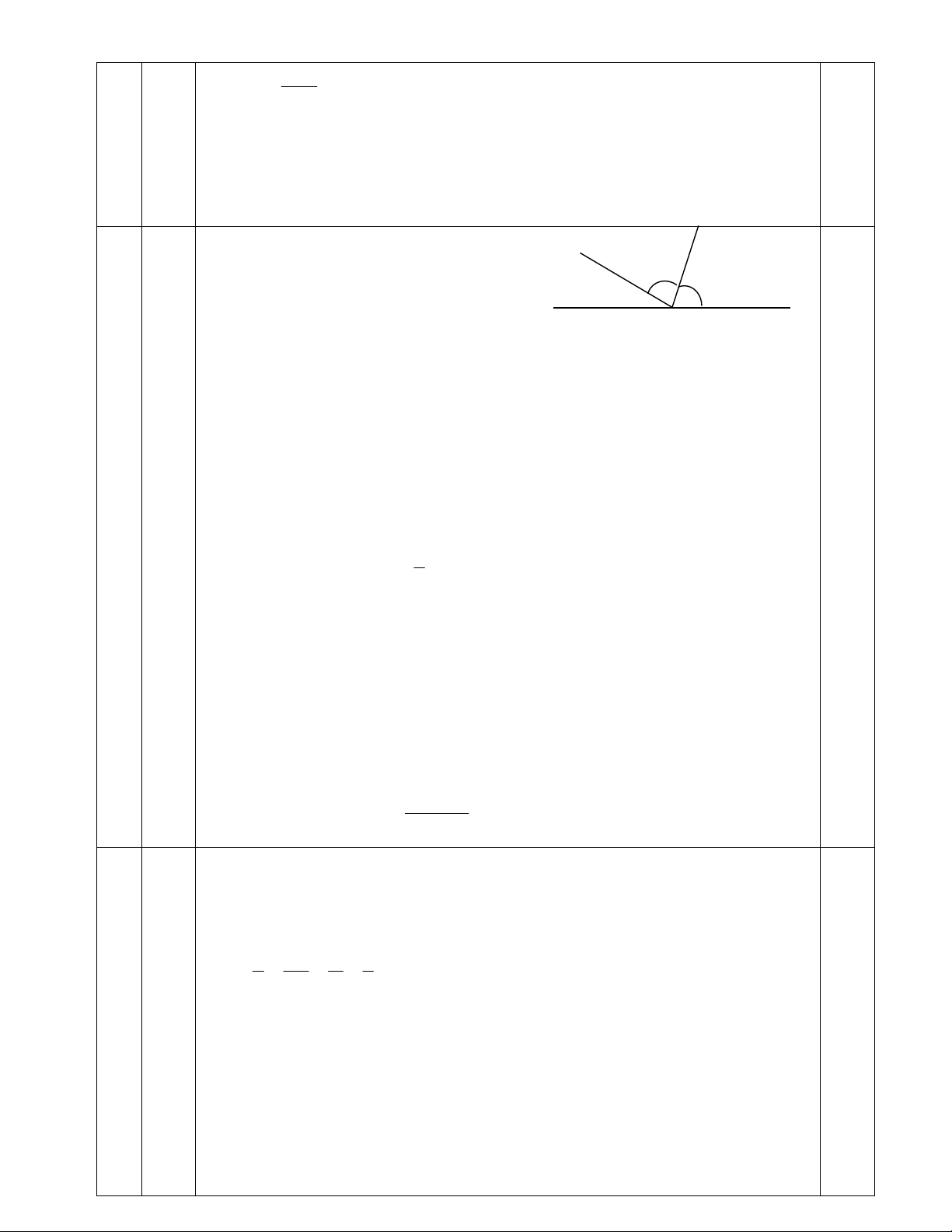
4 (0,5đ) Vẽ hình chính xác z m 0,5 (4,0) x y O 1a Ta có:
(1,5đ) xOz và zOy là hai góc kề bù nên: xOz + zOy =1800 0,25 0,5
mà zOy = 4. xOz nên: 5. xOz = 1800
Do đó: xOz = 1800 : 5 = 360 ; zOy = 4. 360 = 1440 0,75
1b Vì Om là tia phân giác của góc zOy nên: (1,0đ) 1
zOm = mOy = zOy = 720. 2 0,25
Ta lại có: xOm + mOy =1800 0,25
Do đó xOm =1800 - mOy = 1800 - 720 = 1080 0,5
2 - Mỗi đường thẳng cắt 2014 đường thẳng còn lại tạo ra 2014 giao điểm. 0,25
(1,0đ) - Có 2015 đường thẳng nên có: 2014.2015 = 4058210 giao điểm. 0,25
- Do mỗi giao điểm đã tính hai lần nên số giao điểm là:
4058210 2029105 (giao điểm) 0,5 2 5 1 Gọi ƯCLN (a,b) = d
(2,5) (1,5đ) a md Ta có:
(m,n,d N * và (m,n) =1) b nd 0,25 Ta lại có: 5a = 4b a md m 4 0,5 b nd n 5 Mà: (m,n) =1 m 4 n 5 a 4d 0,25
b 5d Mặt khác: BCNN(a,b) = 140 4.5.d 140 0,25 d =140:20 = 7 a 4.7 28 b 5.7 35
Vậy a =28 và b =35 thì thỏa mãn đầu bài. 0,25
Gọi d là ước chung lớn nhất của 8a + 3b và 5a + 2b 2 8
a 3bd (1,0đ) Ta có: 5
a 2bd 5
8a 3bd 0,25 8
5a 2bd
85a 2b 58a 3bd
40a 16b 40a 15bd bd (1) Ta lại có: 0,25 8
a 3bd
5a 2bd 2
8a 3bd 3
5a 2bd
28a 3b 35a 2bd
16a 6b 15a 6bd ad (2) Từ (1) và (2) d ƯC(a,b)
Mà a, b là hai số nguyên tố cùng nhau, nên (a,b) = 1 0,25 d = 1
8a 3b là phân số tối giản. 5a 2b 0,25 Ghi chú:
- Hướng dẫn chấm chỉ nêu một cách giải cho từng bài. Nếu học sinh làm cách
khác đúng thì cho điểm tương đương.
- Câu 4.1 hình vẽ sai hoặc không vẽ hình thì không chấm lời giải.
- Điểm bài thi của thí sinh là tổng điểm của tất cả các câu, không làm tròn.




