



Preview text:
UBND HUYỆN PHÚ THIỆN
ĐỀ THI HỌC SINH GIỎI LỚP 7 CẤP HUYỆN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Môn: Toán ĐỀ CHÍNH THỨC Năm học: 2009-2010
Thời gian: 120 phút (không kể thời gian giao đề)
Bài 1: Thực hiện phép tính (6 điểm). a. 3 2 5 9 : . ; 4 3 9 4 1 1 1 b. 45 1 1 1 ; 19 2 3 4 15 9 20 9 c. 5.4 .9 4.3 .8 . 10 19 29 6 5.2 .6 7.2 .27 Bài 2: (6 điểm)
a. Tìm x, biết: 2(x-1) – 3(2x+2) – 4(2x+3) = 16; b. Tìm x, biết: 3 1 21 : 2x 1 = 2 22
c. Tìm x, y, z biết: 2x y 3y 2z và x + z = 2y. 5 15
Bài 3: (1,5 điểm) Cho tỉ lệ thức a c . b d
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d).
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia
đối của tia KA lấy D , sao cho KD = KA. a. Chứng minh: CD // AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng: ABH = CDH.
c. Chứng minh: HMN cân.
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11. Hết
Họ và tên học sinh:.............................................................; SBD:............................
Học sinh trường:......................................................................................................... UBND HUYỆN PHÚ THIỆN ĐÁP ÁN VÀ BIỂU ĐIỂM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI HỌC SINH GIỎI LỚP 7 CẤP HUYỆN Môn: Toán ĐỀ CHÍNH THỨC Năm học: 2009-2010
Thời gian: 120 phút (không kể thời gian giao đề)
Bài 1: Thực hiện phép tính (6 điểm). Giải: a. 3 2 5 9 : . 4 3 9 4 3 2 5 9 3 1 9 : : 0,75đ 4 3 9 4 4 9 4 = 3 9 9 36 . 9 0,75đ 4 1 4 4 1 1 1 b. 45 1 1 1 19 2 3 4 1 1 45 1 1 1 1 45 1 19 2 3 4 19 1 1 1,0đ 2 1 4 3 45 26 19 = 1 1,0đ 19 19 19 15 9 20 9 c. 5.4 .9 4.3 .8 10 19 29 6 5.2 .6 7.2 .27 15 9 20 9 1 . 2 5 . 2 9 2 20 . 3 9 5.4 .9 4.3 .8 = 5.2 .3 2 .3 .2 01đ 10 19 29 6 5.2 .6 7.2 .27 10 19 19 29 . 3 6 5.2 .2 .3 7.2 3 . 22 .93185.2 32 01đ 22 .93185.3 7 10 9 1 = 0,5đ 15 7 8 Bài 2: (6 điểm) Giải:
a. Tìm x, biết: 2(x-1) – 3(2x+2) – 4(2x+3) = 16.
2x – 2 – 6x – 6 – 8x – 12 = 16 0,25đ -12x – 20 = 16 0,25đ -12x = 16 + 20 = 36 0,50đ x = 36 : (-12) = -3 0,50đ b. Tìm x, biết: 3 1 21 : 2x 1 = 2 22 1
Nếu x . Ta có: (vì nếu x = ½ thì 2x – 1 = 0) 0,25đ 2 1 21 3 : 2x 1 = 2 22 7 21 : (2x – 1) = 0,25đ 2 22 7 21 7 22 11 2x – 1 = : = . 0,25đ 2 22 2 21 3 11 14 2x = + 1 = 0,25đ 3 3 14 7 1 x = : 2 = > 0,25đ 3 3 2 1 Nếu x . Ta có: 0,25đ 2 1 21 3 : 2x 1 = 2 22 7 21 : (1 - 2x) = 0,25đ 2 22 11 8 -2x = - 1 = 0,25đ 3 3 8 4 1 x = : (-2) = 0,25đ 3 3 2 7 4 Vậy x = hoặc x = 0,25đ 3 3
c. Tìm x, y, z biết : 2x y 3y 2z và x + z = 2y 5 15 Từ x + z = 2y ta có:
x – 2y + z = 0 hay 2x – 4y + 2z = 0 hay 2x – y – 3y + 2z = 0 0,25đ hay 2x – y = 3y – 2z 0,25đ 2x y 3y 2z Vậy nếu:
thì: 2x – y = 3y – 2z = 0 (vì 5 15). 0,25đ 5 15 1
Từ 2x – y = 0 suy ra: x = y 0,25đ 2 1
Từ 3y – 2z = 0 và x + z = 2y. x + z + y – 2z = 0 hay y + y – z = 0 0,25đ 2 3 2 1
hay y - z = 0 hay y = z. suy ra: x = z. 0,25đ 2 3 3
Vậy các giá trị x, y, z cần tìm là: {x = 1 z; y = 2 z ; với z R } 3 3 0,5đ
hoặc {x = 1 y; y R; z = 3 y} hoặc {x R; y = 2x; z = 3x} 2 2
Bài 3: (1,5 điểm) Cho tỉ lệ thức a c . b d
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d)
Ta có: (a+2c)(b+d) = (a+c)(b+2d)
ab + ad + 2cb + 2cd = ab + 2ad + cb + 2cd 0,75đ a c cb = ad suy ra: 0,75đ b d
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên
tia đối của tia KA lấy D , sao cho KD = KA. a. Chứng minh: CD // AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng: ABH = CDH.
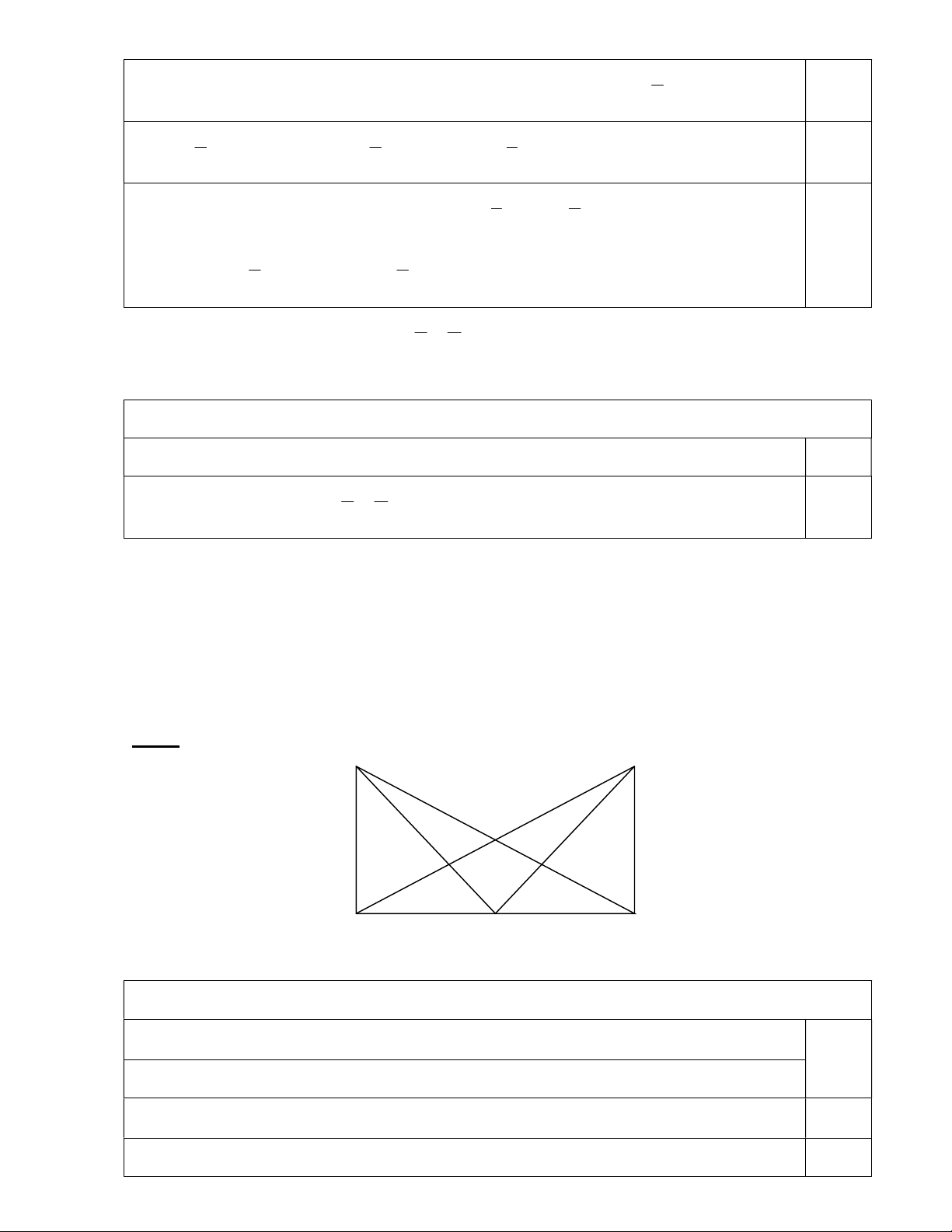
c. Chứng minh: HMN cân. Giải: B D K M N A C H
a/ Chứng minh CD song song với AB.
Xét 2 tam giác: ABK và DCK có: 0,25đ BK = CK (gt) A Kˆ B D Kˆ C (đối đỉnh) 0,25đ AK = DK (gt) 0,25đ ABK = DCK (c-g-c) 0,25đ Cˆ D K K Bˆ D ; mà 0 C Bˆ A B Cˆ A 90 0 Cˆ A D Cˆ A B Cˆ B D 90 0,25đ Cˆ A D 900 C Aˆ B
AB // CD (AB AC và CD AC). 0,25đ
b. Chứng minh rằng: ABH = CDH
Xét 2 tam giác vuông: ABH và CDH có: 0,25đ BA = CD (do ABK = DCK) AH = CH (gt) 0,25đ ABH = CDH (c-g-c) 0,50đ
c. Chứng minh: HMN cân.
Xét 2 tam giác vuông: ABC và CDA có: 0,25đ AB = CD; Cˆ A D 900 C Aˆ B
; AC cạnh chung: ABC = CDA (c-g-c) Cˆ A B D Aˆ C 0,25đ mà: AH = CH (gt) và A Hˆ M C Hˆ N (vì ABH = CDH) 0,50đ AMH = CNH (g-c-g) 0,50đ
MH = NH. Vậy HMN cân tại H 0,50đ
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11. Giải:
Ta có: abcabc = a.105 + b.104 + c.103 + a.102 + b.10 + c 0,25đ
= a.102(103 + 1) + b.10(103 + 1) + c(103 + 1) 0,50đ
= (103 + 1)( a.102 + b.10 + c) 0,50đ
= (1000 + 1)( a.102 + b.10 + c) = 1001( a.102 + b.10 + c) 0,25đ
= 11.91( a.102 + b.10 + c) 11 0,25đ Vậy abcabc 11 0,25đ Hết




