SỞ GD VÀ ĐT HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT PHÙNG KHẮC
NĂM HỌC 2020 – 2021 KHOAN-THẠCH THẤT MÔN THI: TOÁN 10 ĐỀ CHÍ NH THỨC
Thời gian làm bài: 150 phút
(Không kể thời gian phát đề)
Đề thi gồm: 01 trang Câu 1 (2,5 điểm) Cho parabol (P): 2
y = x – 2x + 4 và các đường thẳng (d = + + m): y
3x 2m 1 (m là tham số)
Biện luận số giao điểm của (P) và (dm) theo tham số m. Câu 2 (4,5 điểm)
Giải các bất phương trình sau : a/ f ( x) 1 1 = −  0 b/ 2 2 x 5x 4 5 x 5x 28 x − 3 2 Câu 3 (5 điểm)
1/ Cho lục giác ABCDEF có AB vuông góc với EF và hai tam giác ACE và BDF có
cùng trọng tâm. Chứng minh rằng 2 2 2
AB + EF = CD .
2/ Cho tam giác ABC có các góc thoả mãn hệ thức: cot A + cot C =  cot B . 2 2 2
b + c − a
a.Chứng minh rằng cot A = 4s 1
b. Xác định góc giữa hai đường trung tuyến AA và CC của tam giác ABC khi  = . 1 1 2 Câu 4 (3,0 điểm)
Trong mặt phẳng với tọa độ Oxy, cho tam giác ABC, BE và CD là các đường cao
của tam giác.Giả sử D(2;0), E(1;3) và đường thẳng BC có phương trình : y = 1 - 2x
a/ Tìm tọa độ của M biết M là trung điểm của BC
b/ Tìm tọa độ của điểm B biết B có hoành độ dương Câu 5 (2 điểm) Tìm m để phương trình: 2
4 + x + 4 − x + 2 16 − x = m có nghiệm duy nhất. Câu 6 (3điểm)
Cho các số thực x, y, z thỏa mãn x + y + z = 0, x2 + y2 + z2 = 8. Tìm giá trị nhỏ nhất
của biểu thức S = x + y + z
--------------------HẾT--------------------
Thí sinh không mang tài liệu và máy tính vào phòng thi
Giám thị không cần giải thích gì thêm
Họ và tên thí sinh: ................................................Số báo danh: ............................
Họ và tên, chữ kí CBCT 1: ..................................................................................
Họ và tên, chữ kí CBCT 2: ..................................................................................
SỞ GD VÀ ĐT HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT PHÙNG KHẮC
NĂM HỌC 2020 – 2021 KHOAN-THẠCH THẤT
ĐÁP ÁN MÔN THI: TOÁN 10
Lưu ý: Điểm toàn bài lấy điểm lẻ đến 0,25; thí sinh làm cách khác đúng vẫn cho điểm tối đa. Nội dung Điểm Cho parabol (P): 2
y = x – 2x + 4 và các đường thẳng (d 2,5 m):
y = 3x + 2m + 1 (m là tham số)
1) Biện luận số giao điểm của (P) và (dm) theo tham số m.
Xét phương trình hoành độ: x2 – 2x + 4 = 3x + 2m + 1 1
 x2 – 5x + 3 – 2m = 0 (1). Ta có:  = 8m + 13 Câu 0,5 1 (2,5 +) Nếu 13 m  −
(>0) thì (1) có hai nghiệm phân biệt, do đó (dm) cắt (P) điểm) 8
tại hai điểm phân biệt. +) Nếu 13 0,5 m = −
( = 0) thì (1) có 1 nghiệm kép, do đó (dm) cắt (P) tại 8 một điểm. 13 0, 5 +) Nếu m  −
(  0) thì (1) vô nghiệm, do đó (dm) không cắt (P). 8 Câu
Giải bất phương trình: 1/ f ( x) 1 1 = −  0 2(5, x − 3 2 điểm) 2,0 1 1 1 1 5 − x Ta có −  0  −  0 .   0 x − 3 2 x − 3 2 2.( x − 3) 0,5 − Đặ 5 t
t t = x , bpt trở thành (
 . Cho 5 − t = 0  t = 5 Cho t − ) 0 2 3 0,5
t − 3 = 0  t = 3 Bảng xét dấu a 0,5
Căn cứ bảng xét dấu ta được x  3 hay x  5 . 0,5
Đáp án thi HSG môn Toán 10 - Năm học 2020-2021 Trang 1/4 trang b b) Bất phương trình 2 2 x 5x 4 5 x 5x 28 2,5 Đặt 2 2 2 t x 5x 28 ,t 0 x 5x 4 t 24 0,5
Bất phương trình trở thành 2 t 24 5t 1 2 t 5t 24 0 3 t 8 Suy ra 2 2 x 5x 28 8 x 5x 36 0 9 x 4 0,5
Vậy bất phương trình có tập nghiệm là S 9; 4 0,5 Câu
a/ Cho lục giác ABCDEF có AB vuông góc với EF và hai tam giác ACE 3 (5
và BDF có cùng trọng tâm. Chứng minh rằng 2 2 2
AB + EF = CD . điểm) 2,00
Ta có AB ⊥ EF  A . B EF = 0 suy ra + = ( + )2 2 2 AB EF AB EF (1) 0,5
Mặt khác ACE và BDF có cùng trọng tâm nên AB + CE + EF = 0 (2) có chứng minh 1 Từ (1) và (2) suy ra 2 2 2
AB + EF = CD 0, 5
b/ Tam giác ABC có các góc thoả mãn hệ thức: cot A + cot C =  cot B . 2 2 2
b + c − a Câu 3
1.Chứng minh rằng cot A = (5 điểm) 4s 3đ
2. Xác định góc giữa hai đường trung tuyến AA và CC của tam giác 1 1 1 ABC khi  = . 2 2 2 2
b + c − a
Chứng minh được rằng cot A = 1, 0 4s Ta có: 0, 5 2 2 2 2 2 2 2 2 2
b + c − a
a + c − b
b + a − c cot A = ;cot B = ;cot C = 4s 4s 4s 1 0, 5 Khi  = . Ta có: 2 1 cot A + cot C = cot B 2 2 2 2 2 2 2 2 2 2
b + c − a
a + b − c
1 c + a − b  + = 0, 5 4s 4s 2 4s 2 2 2
 5b = a + c Ta có: 0, 5
Đáp án thi HSG môn Toán 10 - Năm học 2020-2021 Trang 2/4 trang 2 2 2 2 2 2 4 4  b + c a  4 4  a + b c  2 2 2 2 AG = AA =  −
;CG = CC =  −  1 1 9 9  2 4  9 9  2 4  2 2 2 2 4  a + c 
4  5b + 4b  Suy ra 2 2 2 2 AG + CG = b +  = 
 = b  AA ⊥ CC . 1 1 9  4  9  4 
Vậy góc giữa AA và CC bằng 90°. 1 1
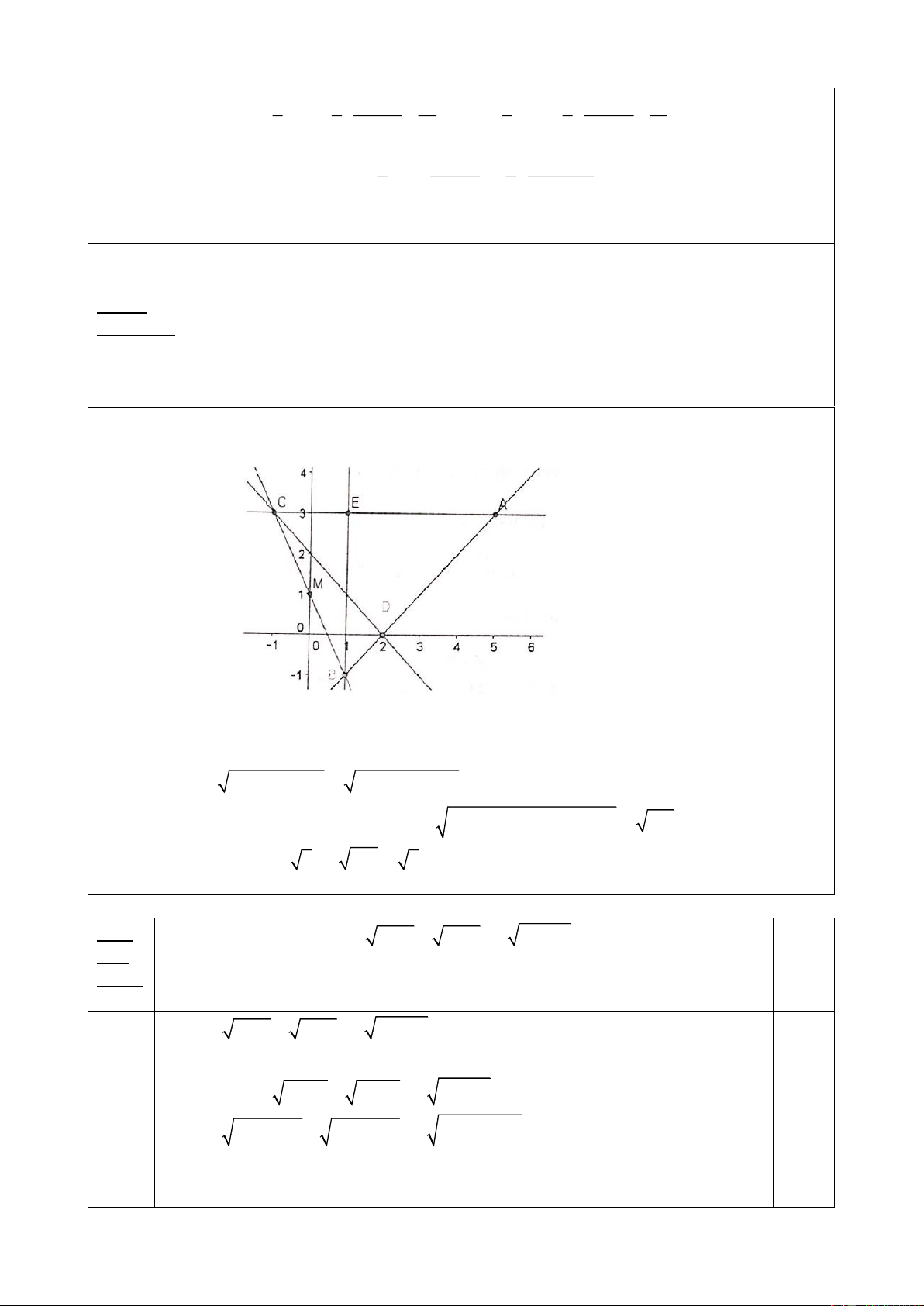
Trong mặt phẳng với tọa độ Oxy, cho tam giác ABC, BE và CD là các
đường cao của tam giác.Giả sử D(2;0), E(1;3) và đường thẳng BC có Câu 4 phương trình (3,0điểm) 2 x + y - 1 = 0. 3,0
a/ Tìm tọa độ của M biết M là trung điểm của BC
b/ Tìm tọa độ của điểm B biết B có hoành độ dương
Gọi M là trung điểm của BC, tứ giác BCDE nội tiếp ta có MD = ME 1 0,5 vẽ hình minh họa Gọi M ( ; m 2 − m + )
1 , ta có MD = ME nên 2 2
 5m −8m + 5 = 5m −10m + 5  m = 0  M (0 ) ;1 , 2 2 0,5
Ta có B (b − b + ) b  MB = (b − ) + (− b + − ) 2 ; 2 1 , 0. 0 2 1 1 = 5b 2
MB = MD = 5  5b = 5,b  0  b = 1  B (1;− ) 1 1,0 Câu Tìm m để phương trình: 2
4 + x + 4 − x + 2 16 − x = m có nghiệm duy 5 (2 nhất. điểm) 2 2
4 + x + 4 − x + 2 16 − x = m (điều kiện 4 −  x  4) 0, 5
Điều kiện cần. Giả sử hệ có nghiệm duy nhất là x 0 Ta có 2
4 + x + 4 − x + 2 16 − x = m 0 0 0 0, 5
4 + (−x ) + 4 − (−x ) + 2 16 − (−x )2 = m 0 0 0
 −x là một nghiệm của phương trình 0
Vì phương trinh duy nhất nên x = −x  x = 0  m = 12 0 0 0
Đáp án thi HSG môn Toán 10 - Năm học 2020-2021 Trang 3/4 trang
Điều kiện đủ: Xét m = 12 phương trình đã cho trở thành 0, 5
2 16 − x  2 16 = 8( 4 + x + 4 − x )2 2 2 = 8 + 2 16 − x = 12 2
4 + x + 4 − x + 2 16 − x  16 0, 5 2
 4 + x + 4 + x + 2 16 − x  4 + 8 = 12
Đẳng thức xảy ra  x = 0 . Phương trình có nghiệm duy nhất x = 0, vậy m = 12.
Câu 6 Cho các số thực x, y, z thỏa mãn x + y + z = 0, x2 + y2 + z2 = 8. Tìm giá trị
(3điểm) nhỏ nhất của biểu thức S = x + y + z 3
S = ( x + y + z )2 2 2 2 2
= x + y + z + 2( x y + y z + z x ) 2 2 2 2
S = x + y + z + x ( y + z ) + y ( z + x ) + z ( x + y ) 0, 5
Áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối ta có +  + = − =  ( + ) 2 y z y z x x x y z  z
Chứng minh tương tự y ( z + x ) 2
 y z ( x + y ) 2 ,  z 1 Vì vậy 2 S  ( 2 2 2
2 x + y + z ) Thay 2 2 2 2
x + y + z = 8  S  16  S  4 1
Dấu bằng có thể xảy ra, khi ( x, y, z) = (2; 2
− ;0) hoặc các hoán vị, ta có 0, 5 S=4 Vậy min S = 4
Đáp án thi HSG môn Toán 10 - Năm học 2020-2021 Trang 4/4 trang