Đề học sinh giỏi Toán 10 năm 2022 – 2023 trường THPT Phùng Khắc Khoan – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT PHÙNG KHẮC KHOAN
CÁC MÔN VĂN HÓA KHỐI 10, 11 - THẠCH THẤT NĂM HỌC 2022-2023
ĐỀ THI MÔN: TOÁN HỌC LỚP 10 ĐỀ CHÍNH THỨC
Thời gian làm bài 150 phút, không kể thời gian giao đề (Đề thi gồm 01 trang)
Số báo danh: ..................... Họ và tên .............................................................................. Câu 1 (5,0 điểm):
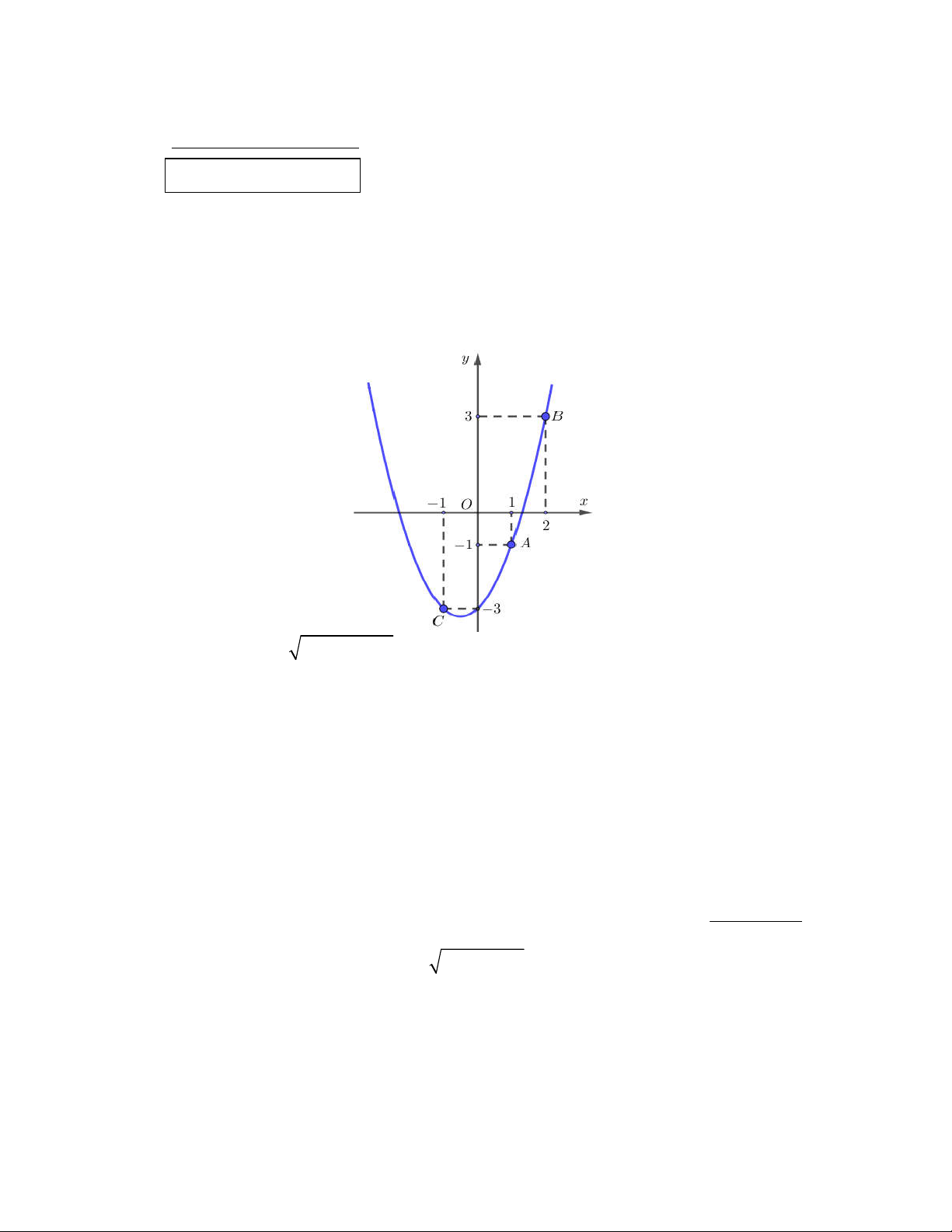
a)Tìm phương trình parabol  P : 2
y  ax  bx  c , biết rằng  P đi qua ba điểm , A B,C như hình vẽ.
b) Giải phương trình 2
3x  4x  4  3x  2 trên tập số thực.
Câu 2 (2,5 điểm): Tìm tất cả các giá trị của tham số thực m để bất phương trình m   2
1 x  2m  
1 x  3m  8  0 đúng với mọi x   . Câu 3 (5,0 điểm):     
a) Cho tam giác ABC lấy các điểm I, J thỏa mãn IA  2IB và 3JA  2JC  0 . Chứng minh
rằng IJ đi qua trọng tâm G của tam giác ABC.
b) Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M 1;2 và hai đường thẳng
d : x  2 y 1  0 , d : 2x  y  2  0 . Viết phương trình đường thẳng  đi qua M và cắt d 1 2 1
tại A, cắt d tại B sao cho MA  2MB . 2
Câu 4 (2,5 điểm): Trong mọi tam giác ABC, gọi a, b, c lần lượt là độ dài các cạnh BC, AC, 2 2 2
a  b  c
AB và S là diện tích tam giác ABC. Chứng minh rằng: cot A  cot B  cot C  . 4S
Câu 5 (2,0 điểm): Cho phương trình 2 2
4 x  4x  5  x  4x  2m 1. Tìm tất cả các giá
trị của tham số m để phương trình có bốn nghiệm thực phân biệt. Câu 6 (3,0 điểm):
Cho x, y, z là số thực. Chứng minh rằng 2 2 2 2 2 2 2 2
x  y  z  x y z  4xyz  y z  2 yz 1  0 .
------------- HẾT -------------
(Thí sinh không dùng tài liệu, cán bộ coi thi không giải thích gì thêm)
Đề thi môn Toán Lớp 10 Trang 1/ 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG CÁC
TRƯỜNG THPT PHÙNG KHẮC
MÔN VĂN HÓA KHỐI 10, 11 KHOAN - THẠCH THẤT NĂM HỌC 2022-2023
ĐỀ THI MÔN: TOÁN HỌC LỚP 10 ĐÁP ÁN CHẤM
Thời gian làm bài 150 phút, không kể thời gian giao đề (Đề thi gồm 01 trang) I. LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài học sinh làm
theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn. II. ĐÁP ÁN: Câu Nội dung trình bày Điểm
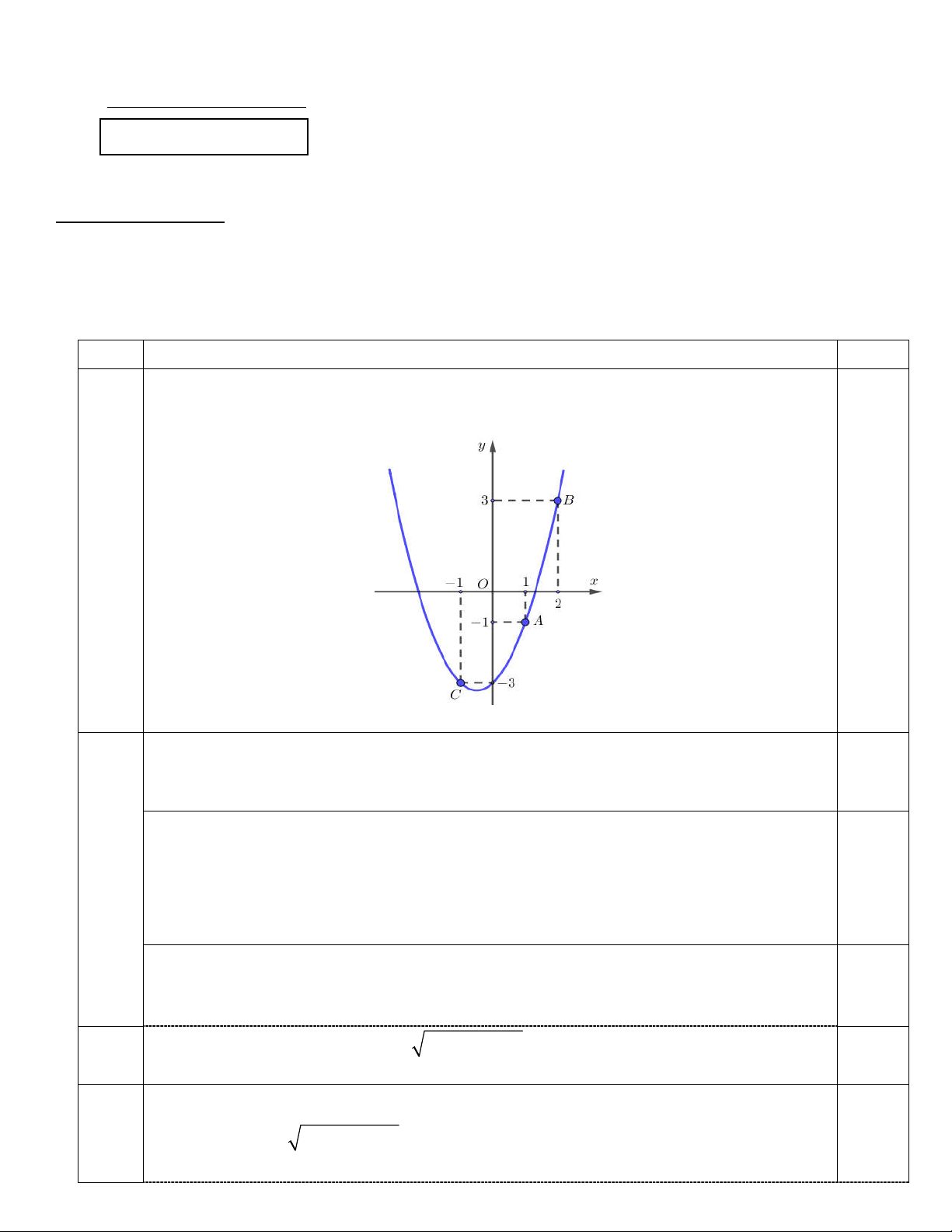
(2,5 điểm) a)Tìm phương trình parabol  P : 2
y  ax  bx  c , biết rằng  P đi qua ba điểm ,
A B,C như hình vẽ. 1.a 2,5
Dựa vào đồ thị ta có  P đi qua ba điểm A1; 
1 , B 2;3 , C 1; 3 . 0,5 2  . a 1  .1 b  c  1  a  1    Ta có: 2  . a 2  . b 2  c  3  b   1   P 2
: y  x  x  3 1,75   . a  2 1  b   1  c  3  c  3    
Vậy  P có phương trình là 2
y  x  x  3. 0,25 1.b
(2,5 điểm) Giải phương trình 2
3x  4x  4  3x  2 trên tập số thực. 2,5 3  x  2  0  1,0 Ta có: 2
3x  4x  4  3x  2  .  2
3x  4x  4   3x  22   2 x     2 3 x      3 
 x  0  x  0 . 1,25  2 6x 16x  0   8  x    3
Vậy tập nghiệm của phương trình là S    0 . 0,25
(2,5 điểm): Tìm tất cả các giá trị của tham số thực m để bất phương trình 2,5 2 m   2
1 x  2m  
1 x  3m  8  0 đúng với mọi x   . 11
Nếu m  1 thì f  x  4x 11  0  x  không thỏa mãn. 4 0,5     0 2   2
 m  3m  9  0
Nếu m  1 thì f  x  0, x        . 1,0 a  0  m 1  0    3  m   ;     3;  3  2      m   . 0,75  2 m  1    3 
Vậy f  x  0, x
    m   ;    . 0,25 2      3.a
(3,0 điểm): Cho tam giác ABC lấy các điểm I, J thỏa mãn IA  2IB và    3,0
3JA  2JC  0 . Chứng minh rằng IJ đi qua trọng tâm G của tam giác ABC.        IA  2IB  0 IA  2IB  Ta có :  
         . 3 1,0
 JA  2JC  0 3 
  IA  IJ   2 IC  IJ   0     
IA  2IB  0        
  2IA  IB  IC  5IJ . 3
 IA  2IC  5IJ 1,0   
 6IG  5IJ ( Với G là trọng tâm của tam giác ABC ) . 1,0
Vậy IJ đi qua trọng tâm G của tam giác ABC.
( 2,0 điểm ) : Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M 1;2 và hai đường
3.b thẳng d : x  2y 1  0 , d : 2x  y  2  0 . Viết phương trình đường thẳng  đi 1 2 2,0
qua M và cắt d tại A, cắt d tại B sao cho MA  2MB . 1 2
Ta có   d  A suy ra A  d nên A1 2a;a ,   d  B suy ra 1 1 2
B  d nên B  ;
b 2  2b . 2   0,25 Suy ra MA   2  ;
a a  2 và MB  b 1; 2
 b  4 .
Do  qua M nên A, B , M thẳng hàng.   MA  2MB 0,25
Hơn nữa MA  2MB , suy ra   . MA  2  MB   2 a     2
 a  2b    1   3
Với MA  2MB     . 0,25 a  2  2   2  b  4 5  b      3  7 2   5 4  Suy ra A  ;   và B  ;   . 0,25  3 3   3 3    2 2  2
Khi đó đường thẳng  qua M 1;2 và nhận AB  ;  .   1;  1 làm  3 3  3 0,25
vectơ chỉ phương nên  : x  y  3  0 .    2  a  2   b   1 a  2  Với MA  2  MB     . a  2  2  0,25   2  b  4 b  3   
Suy ra A3;2 và B  3  ; 4 . 0,25 
Khi đó đường thẳng  qua M 1;2 và nhận AB   6  ;6 làm vectơ chỉ
phương nên  : x  y 1  0 .
Vậy có hai đường thẳng cần tìm:  : x  y  3  0 hoặc  : x  y 1  0 . 0,25
(2,5 điểm): Trong mọi tam giác ABC, gọi a, b, c lần lượt là độ dài các cạnh 4
BC, AC, AB và S là diện tích tam giác ABC. Chứng minh rằng: 2,5 2 2 2
a  b  c
cot A  cot B  cot C  . 4S cos A cos B coC
Từ giả thiết ta có VT  cot A  cot B  cot C    sin A sin B sin C 0,5 2 2 2 2 2 2 2 2 2
b  c  a
a  c  b
a  b  c    a b c 0,75 2b . c 2a . c 2a . b 2R 2R 2R 2 2 2 2 2 2 2 2 2
2R(b  c  a )
2R(a  c  b )
2R(a  b  c ) 0,5    2 . bc a 2a . c b 2 . ab c 2 2 2 2 2 2
R(a  b  c )
a  b  c abc R 1 0,75    VP ( Do S =   ). abc 4S 4R abc 4S
(2,0 điểm): Cho phương trình 2 2
4 x  4x  5  x  4x  2m 1. Tìm tất cả 5
các giá trị của tham số m để phương trình có bốn nghiệm thực phân biệt. 2,0 PT xác định x    . 0,5 Ta có 2 2 x  x 
 x  x  m    2 2 4 4 5 4 2
1 1  x  4x  5  4 x  4x  5  6  2m 2 t 
x  4x  5  t 1; . Phương trình có dạng 2
t  4t  6  2m 2 0,5 Phương trình  
1 có 4 nghiệm x phân biệt khi phương trình 2 có 2 nghiệm t phân 0,5 biệt lớn hơn 1.
Lập BBT cho hàm số f t  2
 t  4t trên 1; ta có phương trình 2 có 2 9 0,5
nghiệm t phân biệt lớn hơn 1 khi f 2  6  2m  f   1   m  5 2
(3,0 điểm): Cho x, y, z là số thực. Chứng minh rằng 6 3,0 2 2 2 2 2 2 2 2
x  y  z  x y z  4xyz  y z  2 yz 1  0 .
Bất đẳng thức viết lại  2 2  y z  2 2 2 2 2 1
x  4xyz  y  z  y z  2 yz 1  0 0,25
Đặt f  x   2 2  y z  2 2 2 2 2 1
x  4xyz  y  z  y z  2 yz 1.
Khi đó f  x là một tam thức bậc hai ẩn x có hệ số 2 2
a  1  y z  0 ; 0,75 và 2 2   y z   2 2  y z  2 2 2 2 ' 4 1
y  z  y z  2 yz   1 . x Ta có 2 2 2 2 4 2 3 3 2 4 4 4
 '  (1 y  2 yz  z  2 y z  y z  2 y z  y z  y z ) 0,5 x 4 2 2 4 3 3
 y z  y z  2 y z   Áp dụng BĐT 2 2
a  b  2ab ta có: 4 4 2 2
 y z 1  2 y z , 0,75  2 2
y  z  2 yz  
Cộng vế với vế lại suy ra  '  0 . Do đó f  x  0, x
 , y, z . ĐPCM. x 0,75
Document Outline

• Toan 10-HSG 2022-2023
• Toan 10-Dap an HSG 2022-2023