

Preview text:
SỞ GD & ĐT THÁI NGUYÊN
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG TRƯỜNG THPT NĂM HỌC 2023- 2024 LƯƠNG NGỌC QUYẾN Môn: TOÁN- LỚP 10
Thời gian làm bài: 150 phút, không kể thời gian phát đề
Họ tên…………………………………….Lớp:…………………….
Số báo danh:……………………………..Phòng thi:………………
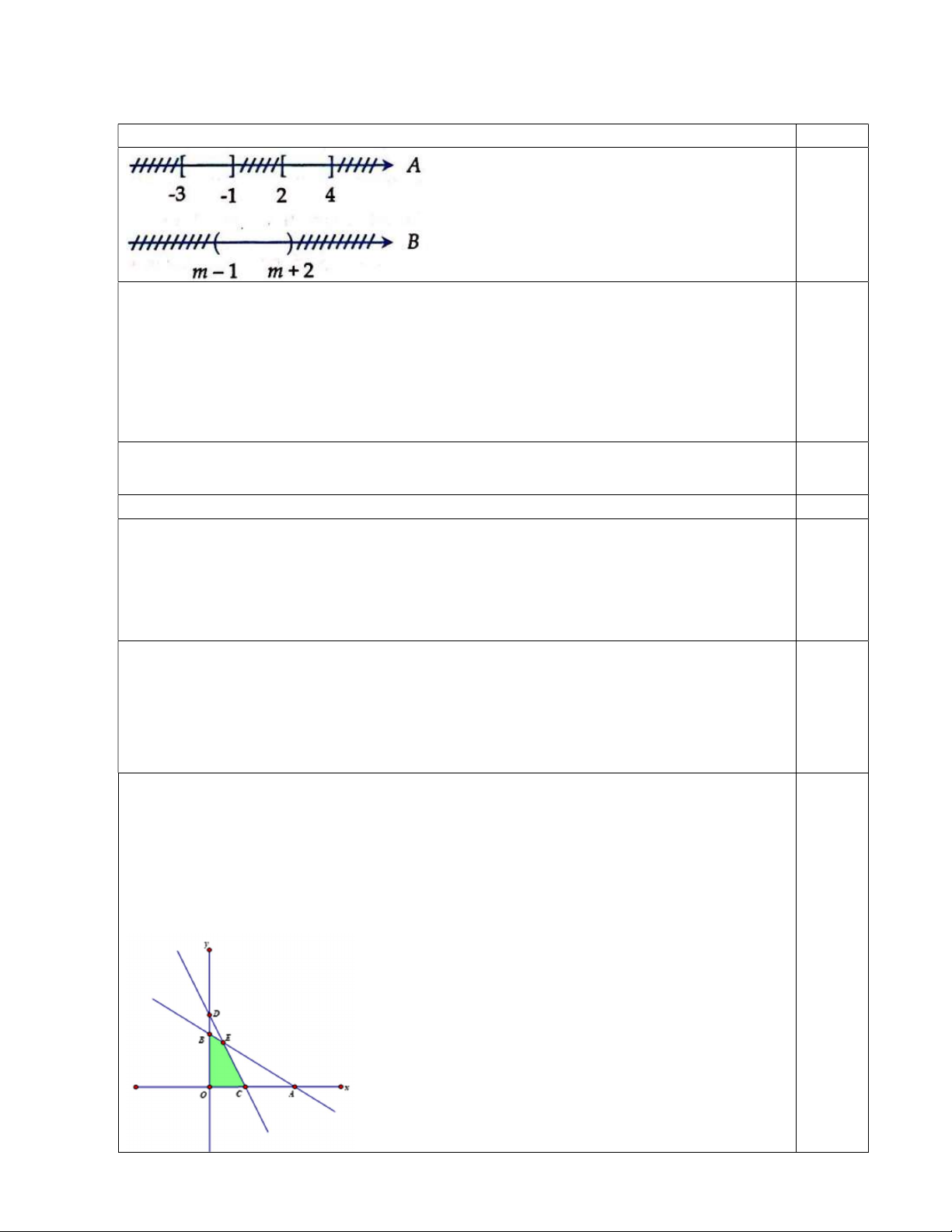
Bài 1: (3 điểm) Cho hai tập hợp A 3;
1 2;4, B m 1; m 2 . Tìm m để A B .
Bài 2: (4 điểm) Một xưởng sản xuất hai loại sản phẩm loại I và loại II từ 200kg nguyên liệu và một máy
chuyên dụng. Để sản xuất được một kilôgam sản phẩm loại I cần 2kg nguyên liệu và máy làm việc trong
3 giờ. Để sản xuất được một kilôgam sản phẩm loại II cần 4kg nguyên liệu và máy làm việc trong 1,5
giờ. Biết một kilôgam sản phẩm loại I lãi 300000 đồng, một kilôgam sản phẩm loại II lãi 400000 đồng
và máy chuyên dụng làm việc không quá 120 giờ. Hỏi xưởng cần sản xuất bao nhiêu kilôgam sản phẩm
mỗi loại để tiền lãi lớn nhất?
Bài 3: (4 điểm) Bạn Mai có ba lọ dung dịch chứa một loại acid. Dung dịch A chứa 10%, dung dịch B
chứa 30% và dung dịch C chứa 50%. Bạn Mai lấy từ mỗi lọ dung dịch và hòa với nhau để có 50g hỗn
hợp chứa 32% acid này và lượng dung dịch loại C lấy nhiều gấp đôi dung dịch loại A. Tính lượng dung
dịch mỗi loại bạn Mai đã lấy. 1 cos . B cosC 4
Bài 4: (3 điểm) Cho tam giác ABC có
. Chứng minh ABC là tam giác đều. 3 3 3 b c a 2 a b c a
Bài 5: (3 điểm) Cho tam giác ABC có trọng tâm G và điểm N thỏa mãn NB 3NC 0 . Gọi P là PA
giao điểm của AC và GN , tính tỉ số . PC
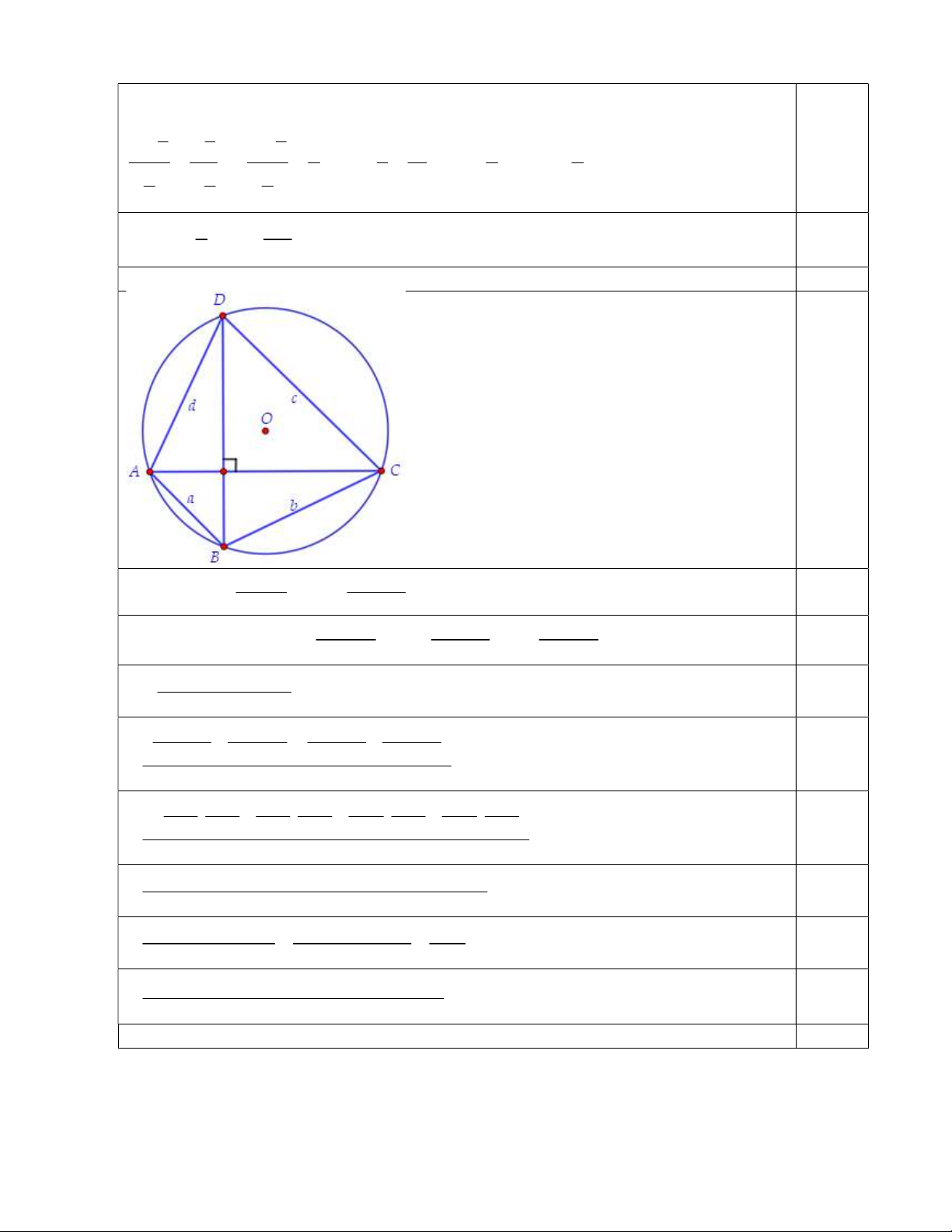
Bài 6: (3 điểm) Cho tứ giác lồi ABCD có AC BD và nội tiếp đường tròn tâm O bán kính R 1 . Đặt
diện tích tứ giác ABCD bằng S và AB a, BC b,CD c, DA d . Tính giá trị biểu thức ab cdad bc T . S ……...HẾT…….
Cán bộ coi thi không giải thích gì thêm.
Học sinh không được sử dụng tài liệu, không được sử dụng máy tính cầm tay. ĐÁP ÁN, BIỂU ĐIỂM Bài 1: 0,5 1,5
Ta đi tìm m để A B
m 2 3 m 5 1 m 1 4 m 5 1 m 1 m 0 m 2 2 5 m 5 A B m 0 Bài 2:
Giả sử sản xuất x(kg) sản phẩm loại I và y(kg) sản phẩm loại II.
Điều kiện x 0, y 0 và 2x 4 y 200 x 2 y 100
Tổng số giờ máy làm việc: 3x 1,5 y 1 Ta có 3x 1,5 y 120
Số tiền lãi thu được là T 300000x 400000 y (đồng). Ta cần tìm , x y thoả mãn: x 0, y 0 x 2y 100 (I) 1 3 x 1,5y 120
sao cho T 300000x 400000 y đạt giá trị lớn nhất.
Trên mặt phẳng tọa độ Oxy vẽ các đường thẳng d : x 2 y 100; d : 3x 1,5y 120 1 2
Đường thẳng d cắt trục hoành tại điểm (
A 100;0), cắt trục tung tại điểm B(0;50) . 1
Đường thẳng d cắt trục hoành tại điểm C(40;0) , cắt trục tung tại điểm D0;80. 2
Đường thẳng d và d cắt nhau tại điểm E20;4 0 . 1 2
Biểu diễn hình học tập nghiệm của
hệ bất phương trình (I) là miền đa giác OBEC . 1 x 0 x 0 x 20 T 0; T 20000000 ; T 22000000 ; y 0 y 50 y 40 x 40 T 12000000 1 y 0
Vậy để thu được tổng số tiền lãi nhiều nhất thì xưởng cần sản xuất 20kg sản phẩm loại I và 40kg sản phẩm loại II. Bài 3:
Gọi lượng dung dịch loại A, B, C mà Mai đã lần lượt lấy ra là ,
x y, z 0 x, y, z 50. 0,5 x y z 50 x y z 50
Theo bài ra ta có hệ phương trình: z 2x z 2x . 1,5 1 3 5 32 1 3 5 x y z .50 x y z 16 10 10 10 100 10 10 10 x 5
Giải hệ trên ta có y 35. 1,5 z 10
Vậy dung dịch loại A, B, C mà Mai đã lần lượt lấy ra là: 5 g,35 g,10 g. 0,5 Bài 4: Ta có: 2
a b c b c 2 2 b bc c 2 2 2 (2) a b bc c (3) 0,5 Theo định lý cos ta có: 2 2 2 a b 2b . c cos A c (4) 1
Từ (3) và (4) suy ra: cos A mà 0 A 180 nên A 60 (*) 0,5 2 2 2 2 2 2 2 a c b a b c 1 Mặt khác (1) . (5) 0,5 2ac 2ab 4 2 2c bc 2 2b bc 2c b2b c
Thế (3) vào (5) ta được: 1 1. 0,5 2 2 b c bc 2 2 bc b c bc
bc b c b c bc b c2 2 2 2 2 5 2 2 3 0 b c (**) 0,5
Từ (*) và (**) suy ra ABC là tam giác đều. (đpcm) 0,5 Bài 5:
Gọi M là trung điểm của cạnh BC. Đặt AP k AC .
1
GP AP AG k AC AB AC 3
1 1 k AC AB . 3 3 1
1 1
GN GM MN AM BC AB AC 7 5 AC AB AC AB 3 6 6 6
Ba điểm G, P, N thẳng hàng nên hai vectơ G , P GN cùng phương. Do đó 1 1 1 k k 2 1 7 4 4 3 3 3 1,5 k k AP AC 7 5 7 5 3 15 5 5 6 6 6 4 PA AP AC 4. 0,5 5 PC Bài 6: 0,5 . a . b AC S .4R Ta có : ABC S ab ABC 4R AC S .4R S .4R S .4R Tương tự ta cũng có : ADC cd , ABD ad , BCD bc 0,5 AC BD BD ab cdad bc T S S .4R S .4R S .4R S .4R ABC ADC ABD BCD AC AC BD BD S S S S S S S S S 4 ABC . ABD ABC . BCD ADC . ABD ADC . BCD AC BD AC BD AC BD AC BD S 4S .S S .S S .S S .S ABC ABD ABC BCD ADC ABD ADC BCD S.AC.BD 4S .S S .S S S S ABC ADC 4 S S ABC ADC 4 . 2 S.AC.BD S.AC.BD S.2S 4 S S S S S S ABC ABD BCD ADC ABD BCD 2 S.AC.BD Vậy T 2 . 0,5 .




