Đề học sinh giỏi Toán 9 năm 2022 – 2023 phòng GD&ĐT Nha Trang – Khánh Hòa

ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH) Bài 1 (6 điểm) − a) Cho 2 2
x − 2y = xy ( y ≠ 0, x + y ≠ 0) . Tính x y A = x + y
Cách 1: (mình cho là cách giải bao quát nhất, áp dụng được cho nhiều dạng toán 2 ẩn)
Đặt x = ky (k ∈), suy ra k ≠ 1
− vì x + y ≠ 0 và k ≠ 0 vì y ≠ 0 Khi đó 2 2 2 2 2 2 2
x − y = xy ⇔ k y − y = ky ⇔ y ( 2 2 2
k − k − 2) = 0  = − ≠ k 1(l) y 0 2 ←
→k − k − 2 ⇔  k = 2 −
Với k = 2 : x = 2y , khi đó 2y y 1 A = = 2y + y 3
Cách 2: (tạo nhân tử) 2 2 2 2 2
x − 2y = xy ⇔ x − y = xy + y ⇔ (x − y)(x + y) = y(x + y)
⇔ (x + y)(x − y) x+ y≠0
2 = 0←→ x = 2y
Cách 3: (Kỹ thuật đồng bậc)  x 2 = 1( − l) x x    y Từ giả thiết 2 2 2 : x − 2 y y = xy ←→ − 2 = ⇔  ⇔ x =   2y  y  y  x = 2   y
Cách 4: (kỹ thuật coi 1 biến làm ẩn) Từ giả thiết 2 2 2 2
x − 2y = xy ⇔ x − .
y x − 2y = 0 (*), với ∆ = (−y)2 2 2 + 8y = 9y y ± ∆
y ± y  y Suy ra (*) 3 2 ⇔ x = = = ⇔ x =  2y 2 2 − y(l) Cách 5:
Lớp TOÁN (Online, offline) NBV 2
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH) 2 2 2 x − y x − y xy + y y (x + y) y A = = = = =
x + y (x + y)2 (x + y)2 (x + y)2 x + y
Suy ra x − y = y ⇒ x = 2y 1 1 1
b) Cho ba số x, y, z thỏa xyz =1 và x + y + z = + + . Chứng minh trong ba số x, y, z có một x y z số bằng 1.
Cách 1: (Phương pháp phản chứng)
Giả sử trong ba số x, y, z không có số nào bằng 1, nghĩa là x, y, z ≠ 1⇒ (x − ) 1 ,( y − ) 1 ,(z − ) 1 ≠ 0 Suy ra (x − ) 1 ( y − ) 1 (z − )
1 ≠ 0 ⇔ (xy − x − y + ) 1 (z − ) 1 ≠ 0
⇔ xyz − xy − xz + x − yz + y + z −1 ≠ 0 1=
⇔ x + y + z ≠ xy + yz + zx 1 1 1
Mặt khác, từ giả thiết x + y + z = + + , ta suy ra x + y + z = xy + yz + xz x y z
Ta dẫn đến một sự mâu thuẫn
Do đó, điều giả sử trên là sai Vậy ta được đpcm.
Lời bình: Lời giả sau đây là sai
“Vì x, y, z ≠ 1 nên xyz ≠ 1 (trái với gt) nên ta suy ra đpcm”
Vì sao lời giải trên là sai ?
Cách 2: (Phương pháp trực tiếp)
Để chứng minh trong ba số x, y, z có một số bằng 1,
Ta phải chứng minh biểu thức A = (x − ) 1 ( y − ) 1 (z − ) 1 = 0
Lớp TOÁN (Online, offline) NBV 3
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Thật vậy, A ⇔ (xy − x − y + ) 1 (z − ) 1 = 0
⇔ xyz − xy − xz + x − yz + y + z −1 = 0 1=
⇔ x + y + z = xy + yz + zx 1 1 1
Mặt khác, từ giả thiết x + y + z = + + , ta suy ra x + y + z = xy + yz + xz x y z Vậy ta được đpcm.
Cách 3: (Nguyên lý “đi dép lê” Dirichlet)
Vì xyz =1⇒ x, y, z ≠ 0
Vì chỉ có 2 dấu + và -, mà có tới 3 số x, y, z nên tồn tại 2 trong 3 số ấy cùng dấu
Không mất tính tổng quát, ta giả sử 2 số ấy là x, y ,
• Trường hợp 1: x, y > 0
Vì xyz =1 nên z > 0
Nếu cả x, y, z >1 thì xyz >1 (trái với gt)
Nếu cả 0 < x, y, z <1 thì xyz <1 (cũng trái với gt)
Như vậy, phải có 1 số trong 3 số ấy bằng 1 (đpcm)
• Trường hợp 2: x, y < 0
Vì xyz =1 nên z > 0, suy ra x, y < 0 < z
Từ đây ta thấy, nếu trong 3 số có 1 số bằng 1 thì số đó là z Nếu z >1 thì 1 1 1 1 1
Từ xyz =1⇒ z =
>1⇒ xy <1⇒ x > ; y > ⇒ x + y > + xy y x x y   Từ giả thiết 1 1 1 + + = + + ⇒ ( + ) 1 1 1 x y z x y − + = −   z x y z  x y  z
Lớp TOÁN (Online, offline) NBV 4
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH) 1 1 Suy ra, 2
− z > 0 ⇒ > z ⇒ z <1 (sai) z z
Nếu 0 < z <1 thì 1 1 1 1 1
Từ xyz =1⇒ z =
<1⇒ xy >1⇒ x < ; y < ⇒ x + y < + xy y x x y 1 1 Tương tự ta suy được 2
− z < 0 ⇒ < z ⇒ z >1 z z
Như vậy, z phải bằng 1
Kết hợp 2 trường hợp ta được đpcm 2 2
Câu 2 (2 điểm): Cho a ≠ 0,b ≠ 0 . Chứng minh rằng: a b 4 3 a b  + + ≥ +   * 2 2 ( ) b a  b a 
Cách 1: (Đặt ẩn phụ) a b 2 2
Đặt u = + , ( u ≥ 2 : xem lời bình), suy ra 2 a b u = + + 2 b a 2 2 b a Khi đó, ( ) 2
* ⇔ u + 2 ≥ 3u ⇔ (u − ) 1 (u − 2) ≥ 0 (**)
Với u ≥ 2 : (**) đúng
Vậy ta đã chứng minh xong Lời bình: a b
1 bđt phụ ta cần nhớ, + ≥ 2(a,b ≠ 0) , dấu “=” xảy ra khi a = b b a
Cách 2: (Tương đương)
Lớp TOÁN (Online, offline) NBV 5
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH) 2 2 (   *) a b  2 2 3 a b  ⇔ + + + ≥ + 2 2  b a   b a    2  a b 
2 a b  1  a b  ⇔ + − + + ≥ + −       1  b a   b a   b a  2
 a b 1  a b  ⇔ + − ≥ + −     1  b a   b a 
 a b 1 a b 2 ⇔ + − + − ≥    0  b a  b a  2 2 2 2
a + b − ab + − ⇔ . a b ab ≥ 0 ab ab
a + b − ab (a − b)2 2 2 ⇔ . ≥ 0 (**) ab ab Vì 2 2
a − ab + b là bình phương thiếu của một hiệu nên 2 2
a − ab + b > 0
Vậy (**) đúng, ta suy ra đpcm.
Câu 3 (2 điểm): Chứng minh rằng nếu n +1 và 2n +1 (n∈) đều là số chính phương thì n chia hết cho 24. Cách 1:
Để chứng minh n chia hết cho 24, ta sẽ chứng minh n3,n8
• Ta chứng minh n chia hết cho 3:
Nếu n = 3k +1 thì n +1 = 3k + 2 : Đây không phải là số chính phương (trái với gt)
Nếu n = 3k + 2 thì 2n +1 = 6k + 5 = 3(2k + )
1 + 2 : Đây không phải là số chính phương (trái gt) Vậy n3
• Ta chứng minh n chia hết cho 8:
Vì 2n +1là số chính phương lẻ nên 2n +1 chia 8 sẽ dư 1 ⇒ 2n8 ⇒ n4
⇒ n là số chẵn ⇒ n +1 là số lẻ, mà n +1 là số chính phương nên n +1 chia 8 sẽ dư 1 ⇒ n8
Lớp TOÁN (Online, offline) NBV 6
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Ta chứng minh được n chia hết cho 24 (đpcm) Cách 2: 2 n +1= a Đặt  ,(a,b∈*) 2 2n +1 = b
• Vì 2n +1: lẻ ⇒ 2
b : lẻ ⇒ b : lẻ Từ 2 2
2n +1 = b ⇒ 2n = b −1 = (b − ) 1 (b + ) 1 , mà (b − ) 1 ,(b + )
1 : chẵn ⇒ n : chẵn
(Tới đây, ta có thể lập luận như cách 1 để suy ra n8)
Ở đây, mình thêm một cách khác để chứng minh n8 Khi n : chẵn ⇒ 2
n +1 = a : lẻ ⇒ a : lẻ Từ 2
n +1 = a ⇒ n = (a − ) 1 (a + )
1 , tích của hai số chẵn liên tiếp nên n8 • Mặt khác, 2 2
a + b = 3n + 2 (**)
Do n : chẵn, a,b : lẻ nên từ (**) suy ra 2 2
a ,b chia 3 dư 1 ⇒ 2
a = n +1 chia 3 dư 1 ⇒ n3
Câu 4 (2 điểm): Hai đội bóng bàn A và B của hai trường THCS thi đấu giao hữu. Biết rằng mỗi
đấu thủ của đội A phải lần lượt gặp đấu thủ của đội B một lần và số trận đấu gấp đôi tổng số đấu
thủ của hai đội. Tính số đấu thủ của mỗi đội.
Gọi x, y (x, y ∈*) lần lượt là số đấu thủ của đội A và B
Theo đề bài ta có: xy = 2(x + y)
Bài toán trở thành: Tìm nghiệm nguyên dương của phương trình xy = 2(x + y)
Cách 1: (Phương pháp sắp thứ tự toàn phần)
Do vai trò x, y như nhau, không mất tính tổng quát, ta giả sử 1≤ x ≤ y
Lớp TOÁN (Online, offline) NBV 7
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Chia 2 vế của pt cho xy , ta được: 1 1 1 2 1 2
= + ⇒ ≤ ≤ ⇒ x ≤ 4 ≤ y 2 y x y 2 x ⇒ x ∈{1;2;3 } ;4
Với x =1: xy = 2(x + y) ⇔ y = 2(1+ y) ⇔ y = 2 − (sai)
Với x = 2 : xy = 2(x + y) ⇔ 2y = 2(2 + y) ⇔ 0 = 4 (sai)
Với x = 3: xy = 2(x + y) ⇔ 3y = 2(3+ y) ⇔ y = 6 (thỏa)
Với x = 4 : xy = 2(x + y) ⇔ 4y = 2(4 + y) ⇔ y = 4 (Thỏa) Vậy ta có các cặp ( ;
x y) = (3;6),(4;4),(6;3)
Ta TỔNG QUÁT bài toán:
Tìm nghiệm nguyên dương của x x ...x = k x + x + + x với k,n nguyên n ... 1 2 ( 1 2 n ) dương
Cách 2: (Biểu thị 1 ẩn theo ẩn còn lại) = ( + ) ⇒ = + ⇒ ( − ) y≠2 2 2 2 2 2 = 2 y xy x y xy x y x y y  → x = y − 2
(dễ dàng chứng minh y ≠ 2 ) 2( y − 2) + 4 4 ⇒ x = = 2 + y − 2 y − 2  y =1  x = 2( − l)  y − 2 = 1 ± y = 3 4  x =  6
Suy ra, để x ∈ ⇒ ∈ ⇒ y − 2 = 2
± ⇒  y = 0(l) ⇒  y − 2   x = 4 y − 2 = 4 ± y = 4   x = 3  y =  6
Lớp TOÁN (Online, offline) NBV 8
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH) ⇒ ( ;
x y) = (3;6),(4;4),(6;3) Cách 3: (Nhân tử)
xy = 2(x + y) ⇒ xy = 2x + 2y ⇒ x( y − 2) = 2y
⇒ x( y − 2) = 2( y − 2) + 4 ⇒ (x − 2)( y − 2) = 4
x − 2 =1; y − 2 = 4 x = 3; y = 6 x, y∈*
x 2 2; y 2 2  → − =
− = ⇒ x = 4; y = 4  
x − 2 = 4; y − 2 =1 x = 6; y =   3 Câu 5 (6 điểm):
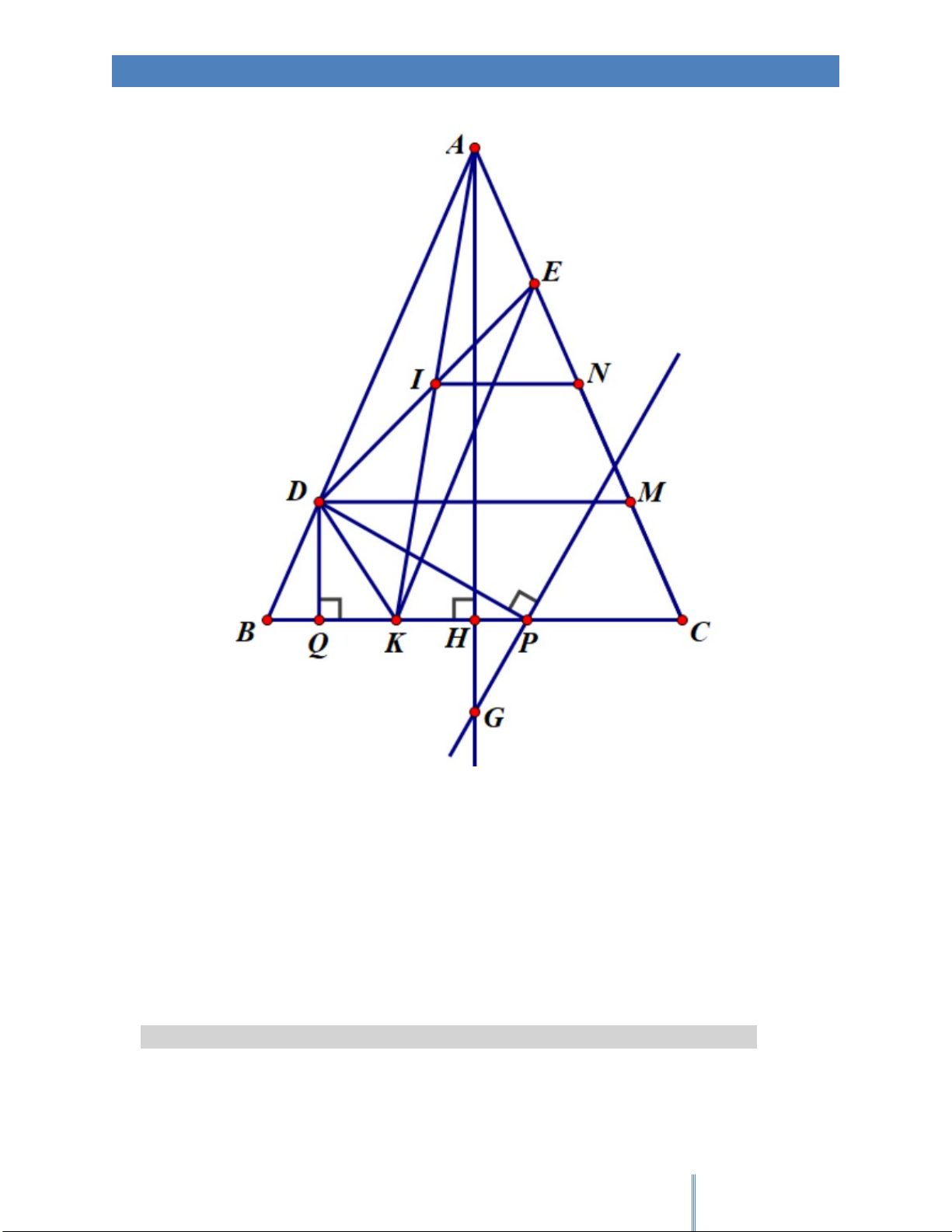
5a. Chứng minh ADKE là hình bình hành.
Lớp TOÁN (Online, offline) NBV 9
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Kẻ DM , IN song song với BCM , N  AC
Chứng minh được AM  CE
Chứng minh được MN  NE
Suy ra N trung điểm của AC
Suy ra I trung điểm của AK
Kết luận ADKE là hình bình hành.
5b. Chứng minh đường thẳng vuông góc với DP tại P luôn đi qua một điểm cố định.
Lớp TOÁN (Online, offline) NBV 10
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Gọi Q, H lần lượt là hình chiếu vuông góc của D và A trên BC . Gỉa sử đường thẳng qua P
vuông góc với DP cắt đường thẳng AH tại G . Ta có 1
BH  BC  QP  BQ  HP 2
Mặt khác, xét hai tam giác vuông QDP và HPG , ta có
             QPG QPD QPD QDP 90
QPG QDP suy ra QDP   HP  G HG HP 2HG HP BQ     
;BQ  HP QP QD BC QD QD 2HG BH BQ BH   (do B  QD và B
 HA đồng dạng nên  ) BC HA QD HA 2 BC.BH BC  HG  
: Không đổi, suy ra G là điểm cố định. 2HA 4AH
Vậy đường thẳng vuông góc với DP tại P luôn đi qua một điểm cố định Câu 6 (2 điểm):
Giả sử mỗi điểm trong mặt phẳng được tô bằng một trong hai màu trắng hoặc đen. Chứng minh
rằng tồn tại một hình chữ nhật có bốn đỉnh cùng màu. Lời giải
Sử dụng (Nguyên lý “đi dép lê” Dirichlet) với “số thỏ”: 9 đường dọc và “số lồng”: 8 cách tô
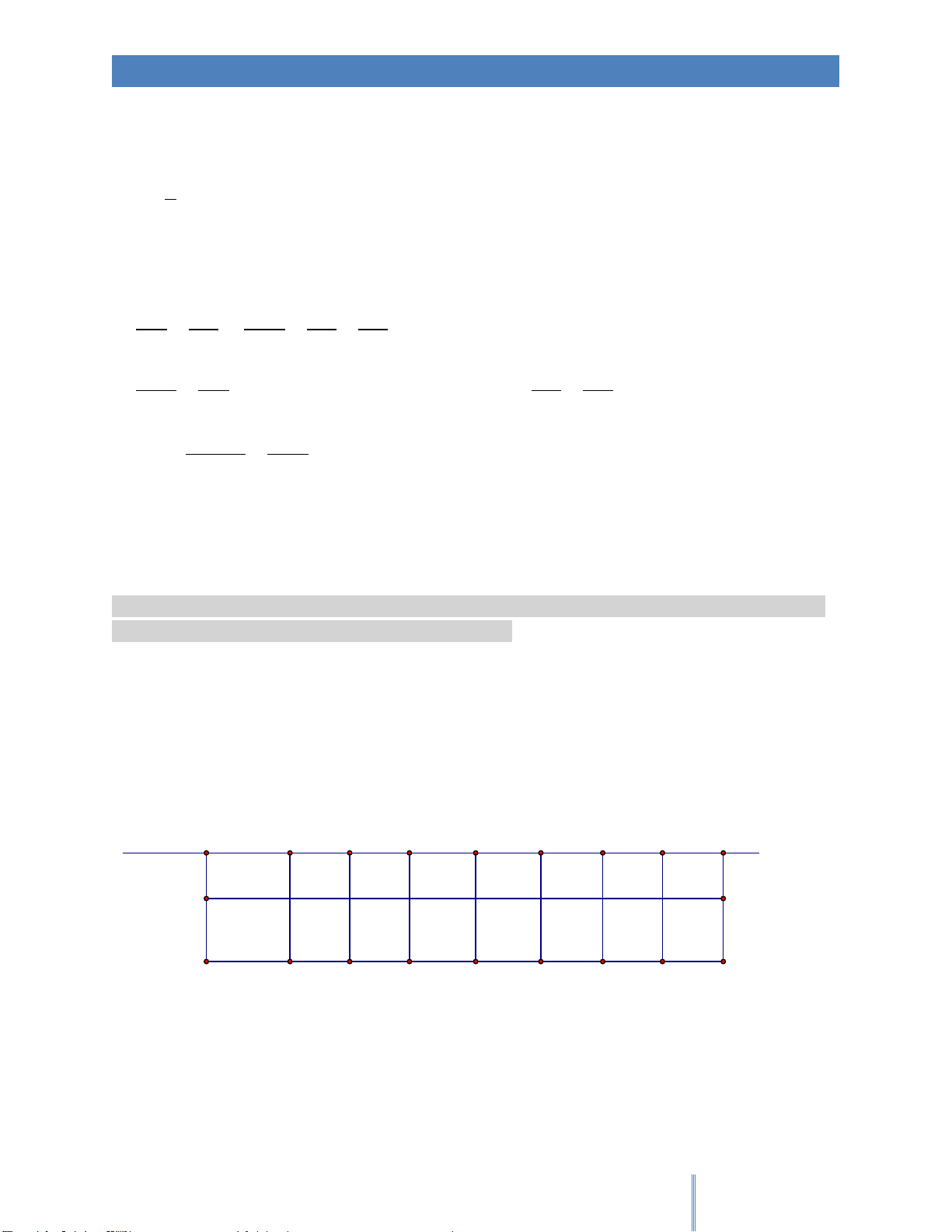
Xét một lưới ô vuông được tại bởi 3 đường nằm ngang và 9 đường kẻ dọc (cột)
Mỗi giao điểm (nút lưới) được tô bởi màu trắng hoặc đen A X B Y C Z
Với 3 điểm trên một đường dọc, mỗi điểm có 2 cách tô (trắng hoặc đen) nên ta có 8 cách tô cho 3
điểm trên cùng một đường dọc
Lớp TOÁN (Online, offline) NBV 11
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Có 9 đường dọc, mỗi đường có 8 cách tô nên theo Dirichlet, tồn tại 2 đường dọc có cùng cách tô màu.
Chẳng hạn hai đường (A, B, C) và đường (X, Y, Z)
Trên 2 đường dọc (cột) có cách tô giống y chang này, trên mỗi cột lại có 2 điểm tô cùng màu
(chẳng hạn B,C) nên tồn tại hình chữ nhật (BYZC) có bốn đỉnh cùng màu.
NHẬN XÉT 1: Ở đây, ta có thể chọn số đường ngang và đường dọc theo các cách sau:
4 đường ngang và 17 đường dọc
5 đường ngang và 33 đường dọc …
n đườn ngang và 2n +1
NHẬN XÉT 2: Cách mình nghĩ ra lời giải
• Vì một hình chữ nhật có 2 đỉnh nằm trên cạnh bên (đường dọc), và mục tiêu là 2 đỉnh này phải cùng màu
Do đó, nếu muốn áp dụng nguyên lý Dirichlet, ta cần tạo ra số điểm nhiều hơn 2 (ta có thể chọn
là 3 điểm), vì khi đó buộc phải có 2 điểm được tô cùng màu
Để có được 3 giao điểm này, ta cần chọn 3 đường kẻ ngang và 1 đường kẻ dọc
• Giờ cần lặp luận để cạnh bên còn lại cũng có cùng cách tô với cạnh bên kia
Trên mỗi cạnh dọc, có 3 điểm, mà mỗi điểm có 2 cách tô (trắng hoặc đen) nên có 8 cách tô trên mỗi đường dọc
Suy ra, muốn áp dụng Dirichlet thì ta cần tạo ra 9 dường dọc
KHAI THÁC & MỞ RỘNG
Lớp TOÁN (Online, offline) NBV 12
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Câu 6A. Giả sử 1 bàn cờ hình chữ nhật có 3x7 ô vuông được sơn đen hoặc trắng. Chứng minh
rằng với cách sơn màu bất kì, trong bàn cờ luôn tồn tại hình chữ nhật gồm các ô ở 4 góc là các ô cùng màu. Hướng dẫn
Mẫu sơn màu có thể xảy ra với bàn cờ này có dạng từ 1 đến 8. Giả sử một trong số các cột thuộc
dạng 1. Bài toán sẽ được chứng minh nếu tất cả các cột còn lại thuộc dạng 1, 2, 3 hoặc 4. Giả sử
tất cả các cột còn lại thuộc dạng 5, 6, 7, 8. Khi đó theo nguyên lí Dirichlet 2 trong số 6 cột có 2
cột cùng 1 dạng và như vậy bài toán cũng được chứng minh.
Chứng minh hoàn toàn tương tự nếu 1 cột có dạng 8. Giả sử không có cột nào trong các
cột 1, 8 thì theo nguyên lí Dirichlet cũng có 2 cột cùng dạng và bài toán cũng đựơc chứng minh.
Câu 6B. Cho mỗi điểm trên mặt phẳng được tô bằng một trong hai màu xanh, đỏ. Chứng minh
rằng tồn tại một tam giác mà ba đỉnh và trọng tâm cùng màu. Lời giải
Lấy năm điểm tùy ý sao cho không có A'
ba điểm nào thẳng hàng trên mặt phẳng. Khi
đó vì chỉ dùng có hai màu để tô các đỉnh, mà
theo nguyên lí Dirichlet phải tồn tại ba điểm A
trong số đó cùng màu. Giả sử đó là ba điểm A, P N G
B, C có màu đỏ. Như vậy ta có tam giác ABC B M C
với ba đỉnh màu đỏ. Gọi G là trọng tâm tam B' C'
giác ABC. Chỉ có hai khả năng xảy ra:
+ Nếu G có màu đỏ. Khi đó A, B, C, G cùng
đỏ và bài toán đã được giải.
Lớp TOÁN (Online, offline) NBV 13
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
+ Nếu G có màu xanh. Kéo dài GA, GB, GC các đoạn AA’ = 3GA, BB’ = 3GB, CC’ = 3GC .
Khi đó gọi M, N, P tương ứng là các trung điểm của BC, CA, AB thì
A’A = 3AG = 6GM ⇒ A’A = 2AM.
Tương tự B’B = 2BN, CC’ = 2CP . Do đó các tam giác A’BC, B’AC, C’AB tương ứng nhận A,
B, C là trọng tâm. Mặt khác, ta cũng có các tam giác ABC và A’B’C’ có cùng trọng tâm G. Có
hai trường hợp sau có thể xảy ra:
• Nếu A’, B’, C’ cùng xanh. Khi đó tam giác A’B’C’ và trọng tâm G có cùng màu xanh.
• Nếu ít nhất một trong các điểm A’, B’, C’ có màu đỏ. Không mất tính tổng quát giả sử A’ đỏ.
Khi đo tam giác A’BC và trọng tâm A màu đỏ.
Vậy trong mọi khả năng luôn tồn tại một tam giác mà ba đỉnh và trọng tâm cùng màu.
Câu 6C. Trong mặt phẳng cho 6 điểm, trong đó không có ba điểm nào thẳng hàng. Mỗi đoạn
thẳng nối từng cặp điểm được tô màu đỏ hoặc xanh. Chứng minh rằng tồn tại ba điểm trong số
sáu điểm đã cho, sao cho chúng là các đỉnh của một tam giác mà các cạnh của nó được tô cùng một màu. Lời giải
Xét A là một trong số 6 điểm đã cho. Khi đó xét B B'
năm đoạn thẳng(mỗi đoạn thẳng nối điểm A với năm
điểm còn lại). Vì mỗi đoạn thẳng được tô chỉ màu đỏ
hoặc màu xanh, nên theo nguyên lí Dirichlet có ít nhất
ba trong năm đoạn nói trên cùng màu. Giả sử đó là các
đoạn AB, AB’ và AB” và có thể cho rằng chúng cùng A B''
màu xanh. Chỉ có hai trường hợp sau xảy ra:
• Trường hợp 1: Nếu ít nhất một trong ba đoạn BB’, B’B”, B”B màu xanh, thì tồn tại một tam
giác với ba cạnh xanh và kết luận của bài toán đúng trong trường hợp này.
• Trường hợp 2: Nếu không phải như vậy, tức là BB’, B’B”, B”B màu đỏ , thì ba điểm phải tìm
là B, B’,B” vì BB’B” là tam giác có ba cạnh màu đỏ. (Đpcm).
Lớp TOÁN (Online, offline) NBV 14
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Câu 6D. Trên đường tròn cho 16 điểm được tô bởi một trong ba màu xanh hoặc đỏ hoặc vàng
(mỗi điểm một màu). Mỗi đoạn thẳng nối hai điểm trong 16 điểm trên được tô màu tím hoặc nâu
(mỗi đoạn thẳng một màu). Chứng minh rằng với mọi cách tô màu ta luôn chọn được một tam giác
có ba đỉnh cùng màu và ba cạnh cùng màu. Lời giải
Trên đường tròn 16 điểm tô bởi ba màu xanh hoặc đỏ A
hoặc vàng và do 16 = 3.5 + 1 nên theo nguyên lý Dirichlet ta F
có ít nhất 6 điểm cùng màu. E
Giả sử 6 điểm đó là A, B, C, D, E cùng màu đỏ như hình vẽ.
Nối AB, AC, AD, AE, AF ta được 5 đoạn thẳng tô bởi hai B D
màu nên theo nguyên lí Dirichlet thì có ít nhất 3 đoạn thẳng C cùng màu.
Giả sử AB, AC, AD có cùng màu nâu. Khi đó ta có các trường hợp sau.
• Trường hợp 1: Nếu một trong ba đoạn BC, BD hoặc CD có màu nâu thì ta có một tam giác có
ba đỉnh màu đỏ và ba cạnh màu nâu.
• Trường hợp 2: Nếu cả ba đoạn BC, BD và CD được tô màu tím thì ta được tam giác BCD có ba
đỉnh màu đỏ và ba cạnh màu tìm.
Vậy ta có điều phải chứng minh.
Câu 6E. Trên mặt phẳng cho 18 điểm, sao cho không có ba điểm nào thẳng hàng. Nối từng cặp
điểm với nhau và tô màu cho mọi đoạn thẳng thu được một trong hai màu xanh và đỏ. Chứng minh
rằng luôn tìm được một tứ giác mà các đỉnh của nó nằm trong tập điểm đã cho sao cho cạnh và
đường chéo của nó cùng màu. Lời giải
Lớp TOÁN (Online, offline) NBV 15
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
Giả sử A (i = 1,18 là 18 điểm đã cho. i ) A A 3 2
Xuất phát từ A có 17 đoạn thẳng A A (i = 2,18 1 i ) 1 A4
. Mười bảy đoạn thẳng đó chỉ có hai màu xanh
hoặc đỏ, nên theo nguyên lí Dirichlet tồn tại ít nhất A5
chín đoạn thằng cùng màu. A6 A1 A
Không giảm tính tổng quát giả sử đó là các 7 A8
đoạn thẳng A A ,A A ,...,A A và chúng cùng 1 2 1 3 1 10 A9
màu đỏ. Xét chín điểm A ,A ,...,A chỉ có thể 2 2 10
xảy ra hai trường hợp sau:
• Trường hợp 1: Hoặc là tồn tại điểm A (2 ≤ j ≤ 10 sao cho trong tám đoạn thẳng j )
A A (2 ≤ k ≤ 10,k ≠ j có ít nhất bốn đoạn màu đỏ. Không mất tính tổng quát có thể cho là j k )
A A ,A A ,A A ,. .,A A màu đỏ. Đến đây lại chỉ còn hai khả năng: 2 3 2 4 2 5 2 6
+ Hoặc là mọi đoạn thẳng A A ,A A ,A A ,A A ,A A ,A A đều màu xanh. Khi đó 3 4 3 5 3 6 4 5 4 6 5 6
A A A A là tứ giác xanh thỏa mãn yêu cầu. 3 4 5 6
+ Tồn tại một đoạn thẳng A ,A (3 ≤ i < j ≤ 6 màu đỏ. Khi đó A A A A (3 ≤ i < j ≤ 6) là tứ i j ) 1 2 i j
giác đỏ thỏa mãn yêu cầu bài toán.
• Trường hợp 2: Hoặc là với mọi điểm A (2 ≤ j ≤ 10 , thì trong tám đoạn thẳng j )
A A (2 ≤ k ≤ 10,k ≠ j có tối đa ba đoạn màu đỏ mà thôi. Khi đó phải tồn tại một điểm (chẳng j k )
hạn A ) mà trong các đoạn A A (3 ≤ k ≤ 10,k ≠ j có tối đa hai đoạn màu đỏ thôi (thật vậy, 2 k ) 2
nếu với mọi A (2 ≤ j ≤ 10 mà có đúng ba đoạn A A (2 ≤ k ≤ 10,k ≠ j màu đỏ, thì số đoạn j k ) j ) 9.3
thẳng màu đỏ nối trong nội bộ 9 điểm đó là
là số nguyên. Vô lí. Vì A A (3 ≤ k ≤ 10,k ≠ j 2 k ) 2
Lớp TOÁN (Online, offline) NBV 16
ÔN THI VÀO 10 & ĐẠI HỌC (ONLINE & OFFLINE) ZALO: 0384 93 77 30 (BÁ VINH)
có tối đa hai đoạn màu đỏ mà thôi, nên trong số các đoạn A A ,A A ,A A ,. .,A A có ít 2 3 2 4 2 5 2 10
nhất sáu đoạn màu xanh. Không mất tính tổng quát ta cho A A ,A A ,...,A A màu xanh. 2 5 2 6 2 10
Xét sáu điểm A ,A ,A ,A ,A ,A . Đó là sáu điểm mà trong đó không có ba điểm nào thẳng 5 6 7 8 9 10
hàng, và mỗi đoạn thẳng nối hai điểm chỉ có hai màu xanh hoặc đỏ. Theo bài 19 thì luôn luôn tồn
tại ít nhất một tam giác mà ba đỉnh chọn trong {A ,A ,A ,A ,A ,A sao cho ba cạnh cùng 5 6 7 8 9 10 }
màu. Lại có hai khả năng:
+ Giả sử tồn tại tam giác A ,A ,A (5 ≤ i < j < k ≤ 10 màu xanh. Khi đó tứ giác A A A A với i j k ) 2 i j k
5 ≤ i < j < k ≤ 10 là tứ giác xanh thỏa mãn yêu cầu đề bài.
+ Nếu tồn tại tam giác A ,A ,A (5 ≤ i < j < k ≤ 10 màu đỏ, thì A A A A là tứ giác cần tìm. i j k ) 1 i j k
Như vậy ta luôn chứng mình được tồn tại một tứ giác mà các đỉnh của nó nằm trong tâm điểm đã
cho sao cho cạnh và đường chéo cùng màu.
Lớp TOÁN (Online, offline) NBV 17
Document Outline

• de-hoc-sinh-gioi-toan-9-nam-2022-2023-phong-gddt-nha-trang-khanh-hoa
• KHAI THÁC ĐỀ HSG LỚP 9 THÀNH PHỐ NHA TRANG