PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH NĂNG KHIẾU TAM NÔNG NĂM HỌC 2023 - 2024 Môn: Toán 6 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút, không kể thời gian giao đề
(Đề thi có 02 trang)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (16 câu – 8,0 điểm)
Câu 1: Có bao nhiêu số tự nhiên x thỏa mãn 5x < 90 ? A. 4. B. 3. C. 2. D. 1.
Câu 2: Tìm số tự nhiên x biết 1+ 2 + 3+...+ x = 465. A. x = 30. B. x = 40. C. x = 50. D. x = 60.
Câu 3: Cho số tự nhiên 23x5y chia hết cho 2, 5 và 9. Khi đó tổng 2024 x + y bằng A. 10. B. 9. C. 8. D. 18.
Câu 4: Tổng các số nguyên x thỏa mãn (x + 3)(x + ) 1 là A. 4. − B. 3. − C. 4. D. 3.
Câu 5: Tìm số tự nhiên n để A = (n + )( 2
1 n + 2024n + 73) là số nguyên số A. n = 3. B. n = 2 . C. n = 0 . D. n =1.
Câu 6: Cho hai số tự nhiên a và b thoả mãn a + b =15,b >a > 3 và UCLN (a,b) = 3. Khi đó tích ab là A. 54. B. 36. C. 72. D. 44.
Câu 7: Hai bạn Nam và Hải thường đến thư viện đọc sách, Nam cứ 8 ngày đến thư viện một lần, Hải
10 ngày một lần. Lần đầu cả hai bạn cùng đến thư viện vào 1 ngày. Hỏi sau ít nhất bao nhiêu
ngày nữa thì hai bạn lại cùng đến thư viện? A. 2. B. 80. C. 18. D. 40. 2023 2023 2023 2023 2023 2023
Câu 8: So sánh hai phân số 9 10 11 P = + + và 9 10 11 Q + + = 2024 2024 2024 11 12 13 2024 2024 2024 11 +12 +13
A. P > Q .
B. P < Q .
C. P = Q .
D. P = 2Q .
Câu 9: Kết quả của phép tính 1 1 1 1 S = + + +...+ là 1+ 2 1+ 2 + 3 1+ 2 + 3+ 4 1+ 2 + 3+...+ 2023 A. 1011. B. 1011 . C. 2023. D. 1011 . 1012 2024 2024 2023 Câu 10: Rút gọn 1 1 1 1   1 1 1 1 P  ...  :  ...  = + + + + + + + +  được kết quả là 2 3 4 2024 4 6 8 4048      A. 1 P = . P = . P = P = 2 B. 2 C. 1. D. 1 . 2024
Câu 11: Để lát nền một phòng học hình chữ nhật người ta dùng loại gạch men hình vuông có cạnh 30cm.
Hỏi cần bao nhiêu viên gạch để lát kín nền phòng học đó? Biết rằng nền phòng học có chiều
rộng 6m và chiều dài 12m(phần mạch vữa không đáng kể). A. 750 viên gạch. B. 800 viên gạch. C. 900viên gạch.
D. 1000viên gạch.
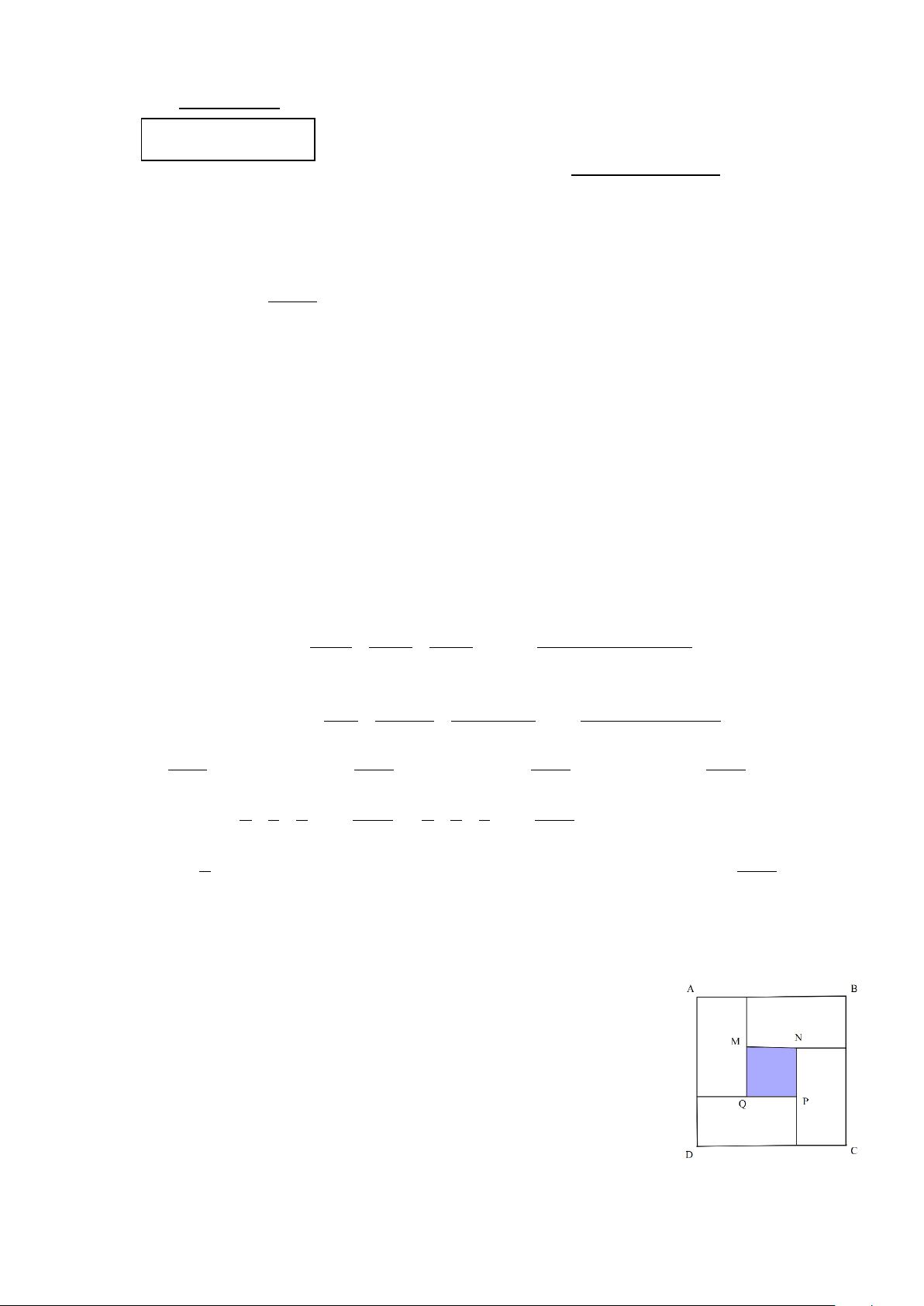
Câu 12: Người ta xếp 4 hình chữ nhật bằng nhau có chiều rộng mỗi hình là
5cm ; chiều dài là 8cm để được một hình vuông ABCD và bên trong là
một hình vuông MNPQ (như hình vẽ). Tính diện tích hình vuông MNPQ . A. 2 64cm . B. 2 25cm . C. 2 160cm . D. 2 9cm .
Câu 13: Cho trước một số điểm. Cứ qua 2 điểm vẽ một đoạn thẳng. Biết rằng có
45 đoạn thẳng. Hỏi có bao nhiêu điểm cho trước? A. 10 điểm. B. 20 điểm. C. 45 điểm. D. 90 điểm. Toán 6 - Trang 1/2
Câu 14: Cho đoạn thẳng MN =1m . Lấy M là trung điểm của đoạn thẳng
M là trung điểm của 1 MN , 2
MM , M là trung điểm của MM , … cứ tiếp tục như vậy cho đến M là trung điểm của 1 3 2 2024 MM
. Tính S = MM + MM + MM +...+ MM . 2023 1 2 3 2024 2024 A. 1 S =1+ . S = . 2 1 1 S − = . S = . 2024 2 B. 2023 2024 C. 2024 2 D. 2024 2
Câu 15: Minh gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau: Số chấm xuất hiện 1 2 3 4 5 6 Số lần 15 20 18 22 10 15
Xác suất thực nghiệm của sự kiện “Số chấm xuất hiện chia cho 3 dư 2 ” là A. 0,4. B. 0,5. C. 0,6. D. 0,3.
Câu 16: Trong một buổi đi tham quan, số nữ đăng ký tham gia bằng 1 số nam. Nhưng sau đó 1 bạn nữ xin nghỉ, 4
1 bạn nam xin đi thêm nên số nữ đi tham quan bằng 1 số nam. Tổng số học sinh đã đi tham quan là 5 A. 20. B. 25. C. 30. D. 35.
II. PHẦN TỰ LUẬN (04 câu – 12,0 điểm) Câu 1 (3,0 điểm) a) Cho 2 3 2024 A = 4 + 4 + 4 +....+ 4
. Tìm số tự nhiên n sao cho 3 4 2 .n A + =
b) Tìm hai số tự nhiên x, y biết 16x + 23y = 376 . Câu 2 (3,0 điểm) 6 20 20 8
a) Rút gọn biểu thức 6.8 .3 20.3 .4 A − = . 16 10 18 6 28.2 .9 −18.2 .27
b) Một trường học tổ chức cho học sinh tham gia hoạt động trải nghiệm tại Đền Hùng. Nếu thuê
các xe 30 chỗ thì thừa 11 ghế, nếu thuê các xe 35 chỗ thì thừa 16 ghế, nếu thuê các xe 45 chỗ
thì thiếu 19 ghế. Hỏi có tất cả bao nhiêu học sinh tham gia? Biết mỗi học sinh chỉ ngồi một ghế
và số học sinh tham gia không quá 700 học sinh. Câu 3 (3,0 điểm). a) Cho 1 1 1 1 1 1 1 S =1− + − +...+ − + − và 2 3 4 2021 2022 2023 2024 1 1 1 1 P = + +...+ + . Tính ( − )2024 S P . 1013 1014 2023 2024 13
b) Cho số tự nhiên n, chứng minh rằng 3n + 8 A = là phân số tối giản. 13 2n + 5 Câu 4 (3,0 điểm).
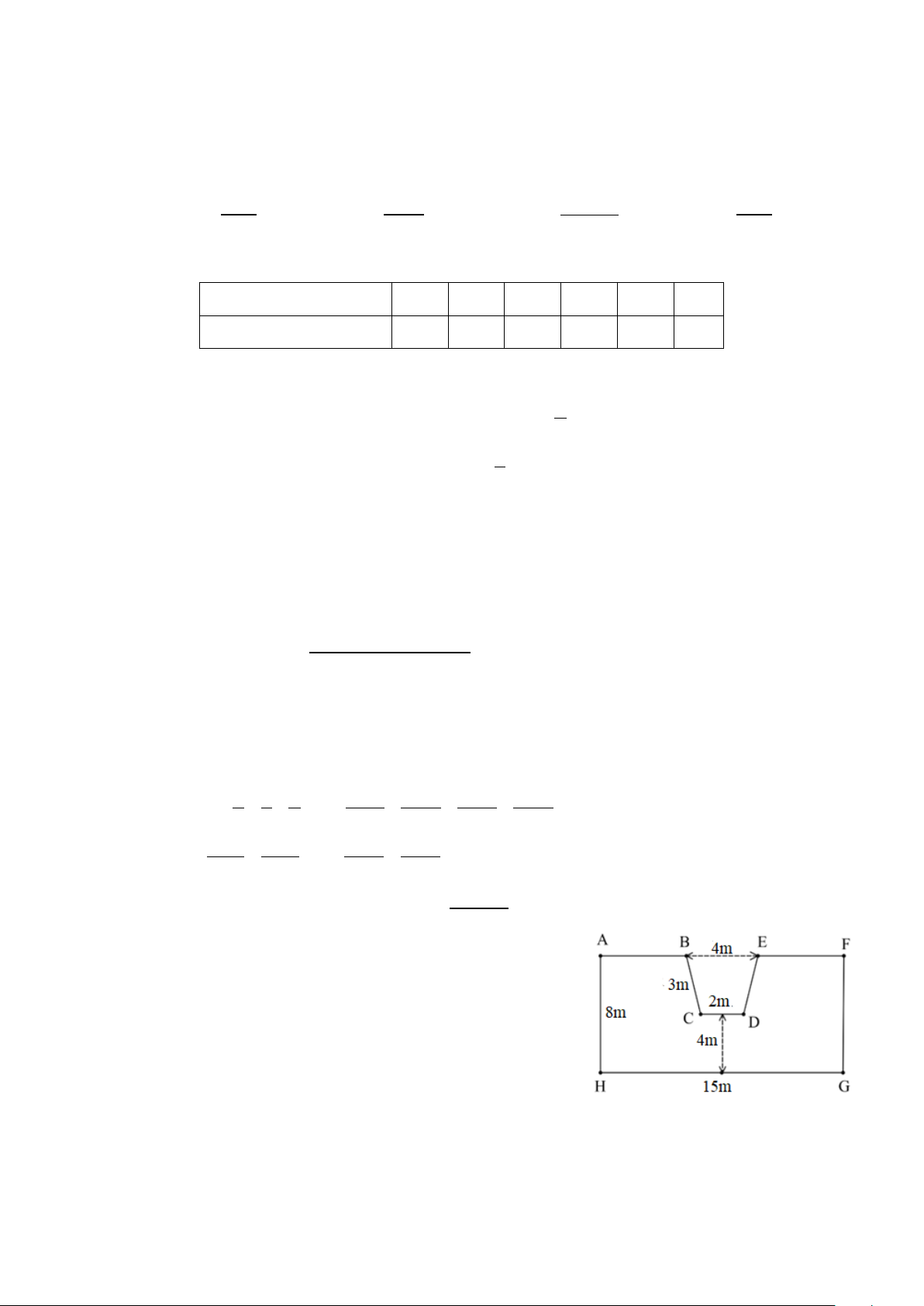
a) Thửa ruộng nhà bác Sơn có dạng ABCDEFGH và kích
thước như hình vẽ, biết AFGH là hình chữ nhật, BEDC là
hình thang cân. Tính chu vi thửa ruộng và số kilôgam
thóc thu được sau mỗi vụ lúa? Biết rằng cứ 2 1m thì bác
Sơn thu hoạch được 0,5kg thóc.
b) Đoạn thẳng AB = 2024cm được chia thành bốn đoạn
thẳng có độ dài không bằng nhau là các đoạn thẳng
AM , MN, NP và PB . Gọi E, F,G, H theo thứ tự là trung điểm của các đoạn thẳng
AM , MN, NP và PB . Biết độ dài của đoạn thẳng EH = a(cm) . Tính độ dài của đoạn thẳng
FG theo a . Toán 6 - Trang 2/2
-------Hết-------
Họ và tên thí sinh:................................................................Số báo danh:............................. Toán 6 - Trang 3/2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO TAM NÔNG
HƯỚNG DẪN CHẤM THI CHỌN HỌC SINH NĂNG KHIẾU NĂM HỌC 2023 - 2024 Môn: Toán 6
A. Một số chú ý khi chấm bài
• Hướng dẫn chấm thi dưới đây dựa vào lời giải sơ lược của một cách, khi chấm thi giám
khảo cần bám sát yêu cầu trình bày lời giải đầy đủ, chi tiết, hợp logic và có thể chia nhỏ đến 0,25 điểm.
• Thí sinh làm bài cách khác với Hướng dẫn chấm mà đúng thì vẫn cho điểm tối đa, tổ chấm
cần thống nhất cho điểm tương ứng với biểu điểm của Hướng dẫn chấm.
• Điểm bài thi là tổng các điểm thành phần không làm tròn số. B. HƯỚNG DẪN CHẤM
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm): Mỗi câu trả lời đúng được 0,50 điểm Câu 1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Đáp án
B A C A C A D A A B B D A C D C
II. PHẦN TỰ LUẬN (12 điểm) Câu Đáp án Điểm Câu 1 (3,0 điểm) a) Cho 2 3 2024 A = 4 + 4 + 4 +....+ 4
. Tìm số tự nhiên n sao cho n 3A + 4 = 2 .
b) Tìm hai số tự nhiên x, y biết 16x + 23y = 376 . a) Ta có 2 3 4 2025 4A = 4 + 4 + 4 +....+ 4 . 1,5 điểm 0,5 2025 3A = 4A - A = 4 − 4 . Khi đó: n 2025 n 2025 3A + 4 = 2 4 4 4 2 4 2n ⇔ − + = ⇔ = . 0,5 4050 2 2n ⇔ = ⇔ n = 4050. Vậy n = 4050. 0,5 b)
- Vì 16x  8, 376  8 mà 16x + 23y = 376 nên 23y  8 0,25 1,5 điểm
- Vì 23y  8 mà (23,8) =1 nên y  8 (1) 0,25
- Vì 16x + 23y = 376 nên 23y <376 => y ≤16 (2)
- Từ (1) và (2) suy ra y ∈{0;8;1 } 6 0,25
+ Thay y = 0vào 16x + 23y = 376 được 47 x = ∉ N nên loại. 0,25 2
+ Thay y = 8 vào 16x + 23y = 376 được x =12 thoả mãn. 0,25
+ Thay y =16vào 16x + 23y = 376 được 1
x = ∉ N nên loại. 2 0,25
Vậy x =12 , y = 8 . Câu 2 (3,0 điểm). 6 20 20 8
a) Rút gọn biểu thức: 6.8 .3 20.3 .4 A − = 16 10 18 6 28.2 .9 −18.2 .27
b) Một Trường học tổ chức cho học sinh tham gia hoạt động trải nghiệm tại Làng văn hoá các dân
tộc Việt Nam. Nếu thuê các xe 30 chỗ thì thừa 11 ghế, nếu thuê các xe 35 chỗ thì thừa 16 ghế, nếu
thuê các xe 45 chỗ thì thiếu 19 ghế. Hỏi có tất cả bao nhiêu học sinh tham gia? Biết mỗi học sinh chỉ
ngồi một ghế và số học sinh tham gia không quá 700 học sinh. Toán 6 - Trang 4/2 a) 0,5 6.8 .3 − 20.3 .4 6.(2 )6 .3 − 20.3 .(2 )8 3 20 20 2 6 20 20 8 1,5 điểm A = = 16 10 18 6 − 16 28.2 .9 18.2 .27 28.2 .( 2 3 )10 18 −18.2 .( 3 3 )6 18 20 2 20 16 18 20 20 18 6.2 .3 − 5.2 .3 .2 6.2 .3 − 5.3 .2 0,5 = = 2 16 20 2 18 18 18 20 18 20 7.2 .2 .3 − 2.3 .2 .3 7.2 .3 − 2.2 .3 (6−5) 20 18 20 18 .3 .2 3 .2 1 0,5 = ( = = . 7 − 2) 18 20 18 20 .2 .3 5.2 .3 5 b)
- Gọi số học sinh tham gia hoạt động trải nghiệm là x (x *
∈ N , 45 < x ≤ 700 ). 0,25 1,5 điểm x +11 30 - Theo đề bài có:  0,25 x +16 35 x −  19 45 x +11− 30 30 x −1930  0,25 x 16 35 35  ⇔ + −
⇔ x −1935 ⇔ x −19∈ BC (30,35,45) . x 19 45  − x −   1945
- Tìm được BCNN (30,35,45) = 630 . 0,25
- Nên x −19∈ B(630) = {0;630;1260;.. }.⇒ x∈{19;649;1279;.. }. . 0,25
+ Vì 45 < x ≤ 700 nên x = 649 . 0,25
Vậy số học sinh tham gia hoạt động trải nghiệm là 649 học sinh. Câu 3 (3,0 điểm). a) Cho 1 1 1 1 1 1 1 S =1− + − +...+ − + − và 1 1 1 1 P = + + ...+ + . 2 3 4 2021 2022 2023 2024 1013 1014 2023 2024 Tính ( − )2024 S P . 13
b) Cho số tự nhiên n, chứng minh rằng 3n + 8 A = là phân số tối giản. 13 2n + 5 a) 1,5   0,5 điểm Ta có 1 1 1 1 1 1 1 1 S =1+ + +...+ + − 2 + +  ...+ + 2 3 2023 2024 2 4 2022 2024    1 1 1 1  1 1 1 0,5 1 ... 1 ...  = + + + + + − + + + + 2 3 2023 2024 2 1011 1012    1 1 1 1 = + + ...+ + = P . 1013 1014 2023 2024
Suy ra S − P = => (S − P)2024 2024 0 = 0 = 0 . 0,5 b) 1,5 13 3
 n +8  d 0,5 điểm Gọi d = ƯCLN( 13 13
3n + 8,2n + 5), Suy ra  13
2n + 5 d ⇒ ( 13 n + ) − ( 13 2 3
8 3 2n + 5) d . 0,5
Hay 1 d ⇒ d =1 ⇒ ƯCLN( 13 13
3n + 8,2n + 5) =1. 0,5 13 Do đó 3n + 8 A = là phân số tối giản. 13 2n + 5 Toán 6 - Trang 5/2 Câu 4 (3,0 điểm).
a) Thửa ruộng nhà bác Sơn có dạng ABCDEFGH và kích
thước như hình vẽ, biết AFGH là hình chữ nhật, BEDC là
hình thang cân. Tính chu vi thửa ruộng và số kilôgam thóc
thu được sau mỗi vụ lúa? Biết rằng cứ 2 1m thì bác Sơn thu
hoạch được 0,5kg thóc.
b) Đoạn thẳng AB = 2024(cm)được chia thành bốn đoạn
thẳng có độ dài không bằng nhau là các đoạn thẳng
AM , MN, NP và PB . Gọi E, F,G, H theo thứ tự là trung điểm của các đoạn thẳng AM , MN, NP
và PB . Biết độ dài của đoạn thẳng EH = a(cm) . Tính độ dài của đoạn thẳng FG theo a . a)
Chu vi của thửa ruộng là: 8 +15 + 8 + (15 − 4) + 3.2 + 2 = 50(m) . 1,5 điểm 0,25
Diện tích hình chữ nhật AFGH là S = = . AFGH ( 2 8.15 120 m ) 0,25
Chiều cao của hình thang cân BCDE là 8 − 4 = 4(m) . 0,25 (4+ 2).4
Diện tích hình thang cân BCDE là S = = . 0,25 BCDE 12 ( 2 m ) 2
Diện tích của thửa ruộng đó là S = S − S = − = . AFGH BCDE ( 2 120 12 108 m ) 0,25
Số kilôgam thóc Bác Sơn thu được sau mỗi vụ lúa là: 108.0,5 = 54kg .
Vậy chu vi thửa ruộng là 50(m) và số kilôgam thóc bác Sơn thu được sau mỗi 0,25 vụ lúa là 54kg . b)
Vì E, F, G, H theo thứ tự là trung điểm của các đoạn thẳng AM, MN, NP và 1,5 điểm PB nên ta có: AM = ; MN = ; NP = ; PB AE FN NG HB = . 0,25 2 2 2 2
Ta có AE + HB = AB − EH = 2024 − a . 0,25 Suy ra AM PB +
= 2024 − a ⇒ AM + PB = 2(2024 − a) = 4048 − 2a . 0,25 2 2
Ta có: MP = AB − ( AM + PB) = 2024 −(4048 − 2a) = 2a − 2024 . 0,25
Theo thứ tự lấy các điểm chia và thứ tự lấy trung điểm các đoạn thẳng, thì N là 0,25
điểm nằm giữa hai điểm F và G; N là điểm nằm giữa hai điểm M và P. Do đó
MN NP MP 2a − 2024 . 0,25
FG = FN + NG = + = = = a −1012 2 2 2 2
Vậy FG = a −1012 (cm). Toán 6 - Trang 6/2