Đề học sinh năng khiếu Toán 6 năm 2023 – 2024 trường THCS Thanh Thủy – Phú Thọ

TRƯỜNG TRUNG HỌC CƠ SỞ THANH THUỶ
ĐỀ THI CHỌN HỌC SINH NĂNG KHIẾU LỚP 6,7,8 THCS – CẤP TRƯỜNG NĂM HỌC 2023 - 2024 Đề chính thức MÔN: TOÁN 6
Thời gian làm bài: 120 phút, không kể thời gian giao đề. Đề thi có: 04 trang
PHẦN I: TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN (4,0 điểm): Hãy chọn phương án
trả lời đúng và ghi vào bài làm.
Câu 1. Tính giá trị của P = ( 11 12 + ) ( 9 2 9 3 5.3
4.3 : 3 .5 − 3 .2 )được kết quả là A. 11 B. 12 C. 15 D. 9
Câu 2. Cho a = 5300 và b = 3500. Kết luận nào sau đây đúng?
A. a < b B. a = b C. a > b D. a ≤ b
Câu 3. Số các số tự nhiên chia hết cho 4 gồm bốn chữ số, chữ số tận cùng bằng 2 là A. 350 B. 450 C. 465 D. 415
Câu 4. Tất cả các số tự nhiên n để 2n + 7 chia hết cho n + 2 là
A. -1 và 1 B. 0 C. 1 D. 2
Câu 5. Cho hai số A = 11 . 12 . 13 + 14 . 15 và B = 11 . 13. 15 + 17 . 19 . 23. Chọn đáp án đúng trong các đáp án sau:
A. Cả A và B đều là số nguyên tố
B. Cả A và B đều là hợp số
C. A là số nguyên tố và B là hợp số
D. A là hợp số và B là số nguyên tố
Câu 6. Cho biết n là số tự nhiên thỏa mãn 1
2n− là số nguyên tố, p là số nguyên tố thỏa mãn p + 2 và
p + 4 đồng thời là hai số nguyên tố.khi đó tổng n + p là: A. 2. B. 3. C. 5. D. 7.
Câu 7. Cho số tự nhiên a , khi chia a cho 4 được số dư là 3, khi chia a cho 9 được số dư là 6 . Số dư khi chia a cho 36 là A. 15 B. 18 C. 27 D. 3
Câu 8. Khối 6 của một trường có khoảng 200 học sinh đến 250 học sinh. Khi xếp hàng 10, hàng 12,
hàng 15 đều dư ra 4 học sinh. Số học sinh khối 6 của trường là A. 244 B. 240 C. 236 D. 245
Câu 9. Giá trị của biểu thức M = 1 + 3 + 5 + 7 + ... + 2023 là A.2048288 B.1024144 C. 2032024 D. 2012022
Câu 10. Giá trị của 1 2 3 4 5 30 31
C = ⋅ ⋅ ⋅ ⋅ ⋅...⋅ ⋅ bằng 4 6 8 10 12 62 64 A. 1 . B. 1 . C. 1 . D. 1 . 31 2 30 2 32 2 36 2 1 Câu 11. Cho 1 1 1 1 B = + + + ...+
khi đó số 2022.B có giá trị bằng 2.4 4.6 6.8 2020.2022 A. 1 B. 1010 C. 505 D. 2020
Câu 12. Một thửa ruộng hình chữ nhật có chu vi 200 m. Chiều dài hình chữ nhật hơn hai lần chiều
rộng là 10m. Tính diện tích hình chữ nhật đó. A. 1200 m2 B. 2100 m2 C. 200 m2 D. 100 m2
Câu 13. Hình thoi A có độ dài hai đường chéo gấp đôi độ dài hai đường chéo của hình thoi B. Hỏi
hình thoi A có diện tích gấp mấy lần diện tích hình thoi B? A. 2 lần B. 3 lần C. 4 lần D. 6 lần
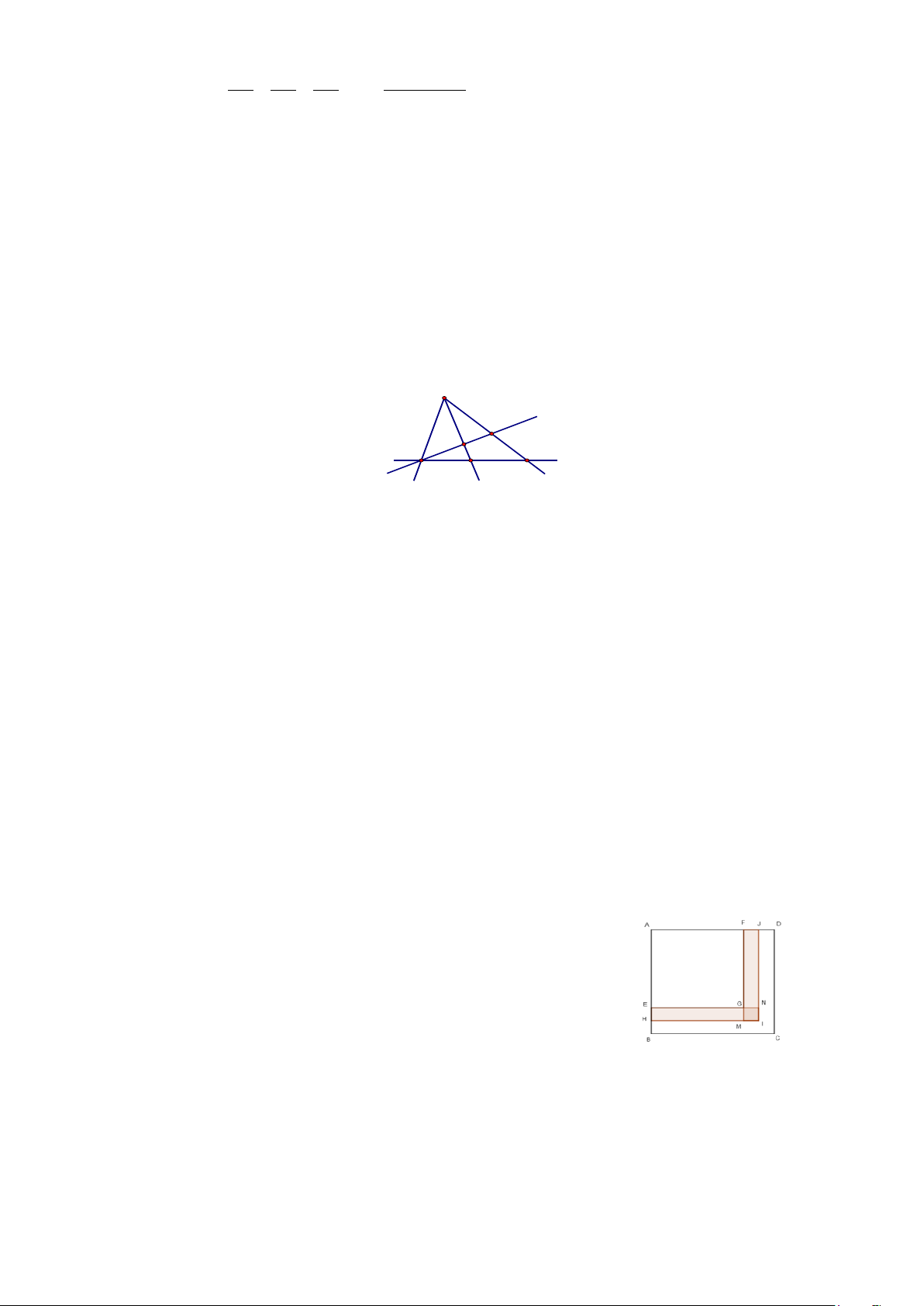
Câu 14. : Trên hình vẽ sau có bao nhiêu hình tam giác? A E F B C D A. 7 B. 8 C. 4 D. 6
Câu 15. Cho lần lượt vào hộp bắt đầu bằng các viên bi xanh, đỏ, tím, vàng, rồi lại xanh, đỏ, tím, vàng.
Cứ tiếp tục như thế cho đến hết 2023 viên bi. Hỏi viên bi thứ 2018 là viên bi màu gì?
A. xanh B. đỏ C. tím D. vàng
Câu 16. Lớp 6A có 15 bạn thích môn Ngữ văn, 20 bạn thích môn Toán. Trong số các bạn thích Ngữ
văn hoặc thích Toán có 8 bạn thích cả hai môn Ngữ văn và Toán. Trong lớp vẫn còn có 10 bạn không
thích môn nào (trong hai môn Ngữ văn và Toán). Hỏi lớp 6A có bao nhiêu bạn tất cả? A. 52. B. 40. C. 37. D. 45.
PHẦN II: TRẮC NGHIỆM ĐÚNG - SAI (2,0 điểm): Ghi câu trả lời Đúng ( Đ) – Sai ( S) trước mỗi khẳng định sau:
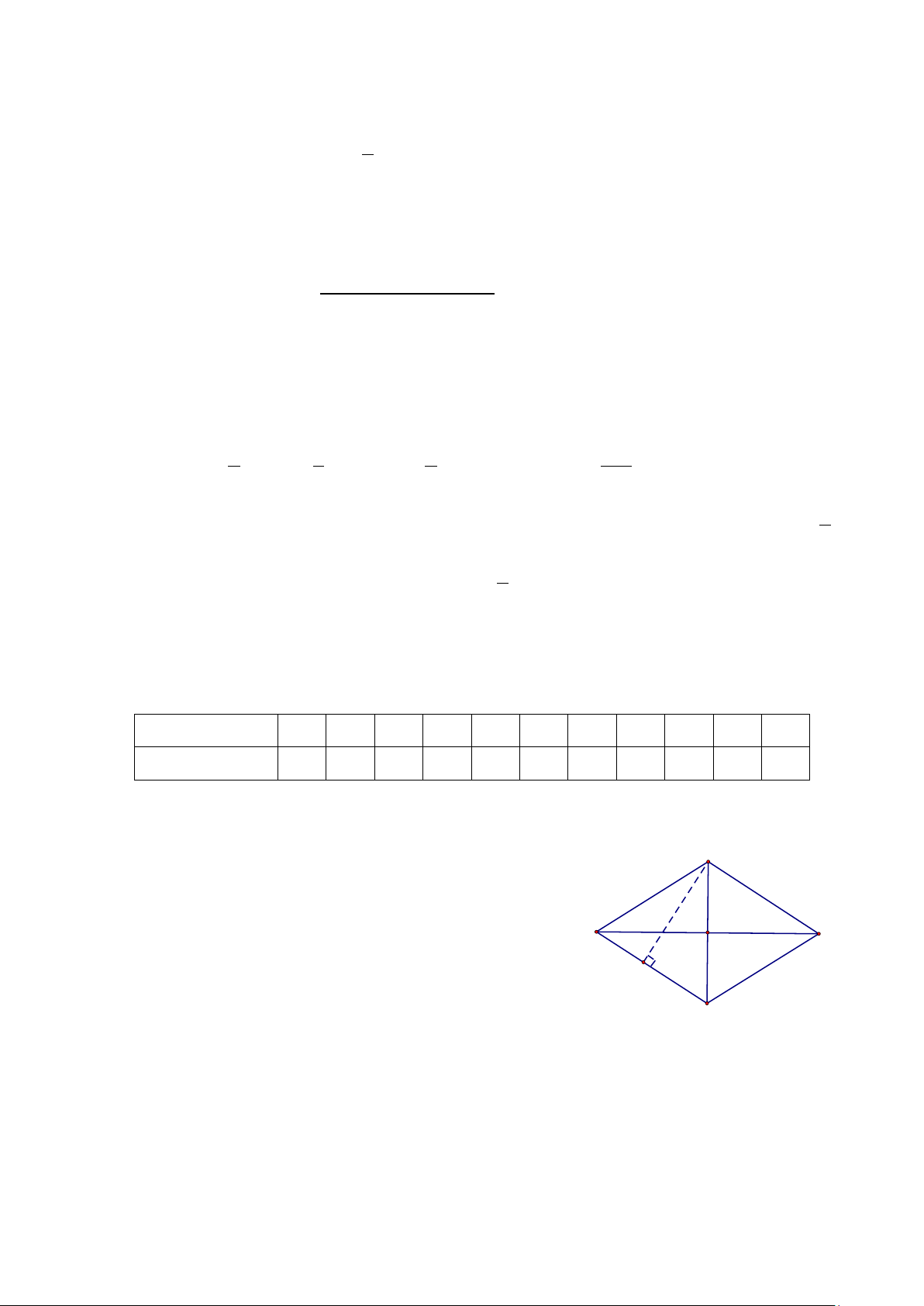
Câu 1. Cho các hình vuông ABCD, AHIJ, AEGF và H là trung điểm của đoạn BE (Hình vẽ). Độ dài
các cạnh của các hình vuông nói trên (theo đơn vị tính là cm) đều là các số tự nhiên, biết rằng diện tích
phần tô đậm là 19 cm2. Khi đó:
A. Trên hình vẽ có tất cả 3 hình vuông
B. Diện tích hình chữ nhật EGMH bằng hình chữ nhật GFJN.
C. Diện tích hình vuông AFGE là 81 cm2.
D. Diện tích hình vuông ABCD là 121 cm2.
Câu 2. Giả sử có n(n ≥ 2) đường thẳng đồng qui tại O thì số góc tạo thành là
A. Số các tia tạo thành là: n(n−1) (tia)
B. Số các tia tạo thành là: 2n (tia)
C. Số các góc tạo thành là: n(n−1):2 (góc)
D. Số các góc tạo thành là: 2n(2n − 1):2 (góc) 2
PHẦN III: TỰ LUẬN (14,0 điểm): Câu 1 (4,0 điểm).
a) Tìm số tự nhiên x, biết: 3x−2 1 5 5 5 + 3 .5 = 28,5.5 2
b) Tìm số nguyên tố p sao cho p + 6, p + 8, p +12, p + 24 cũng là các số nguyên tố. Câu 2 (3,0 điểm). 6 4 9 5.4 .9 -3 .(-8)4
a) Rút gọn biểu thức sau: C = 13 8 4 3 4.2 .3 + 2.8 .(-27)
b) Tìm các số tự nhiên x, y, z nhỏ nhất khác không sao cho 24.x = 36.y = 54.z Câu 3: (3,0 điểm).
a) Tính giá trị của các biểu thức sau: 1 1 1 1
1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) + …+ (1 + 2 + …+ 200) . 2 3 4 200
b) Một đội công nhân phải vận chuyển hết số thóc trong kho. Ngày đầu đội đó vận chuyển được 1 số 4
thóc và 15 tấn, ngày thứ hai đội đó vận chuyển được 5 số thóc còn lại và 20 tấn, ngày thứ ba đội đó 9
vận chuyển được 75% số thóc còn lại và 20 tấn cuối cùng. Hỏi kho đó có bao nhiêu tấn thóc?
Câu 4: (1,0 điểm). Bình gieo hai con xúc xắc cùng lúc 50 lần. Ở mỗi lần gieo, Bình cộng số chấm xuất
hiện ở hai con xúc xắc và ghi lại kết quả như bảng sau: Tổng số chấm 2 3 4 5 6 7 8 9 10 11 12 Số lần 2 5 4 7 8 7 5 4 3 3 2
Tính xác suất thực nghiệm số lần xuất hiện tổng số chấm ở hai con xúc xắc lớn hơn 6. Câu 5: (3,0 điểm).
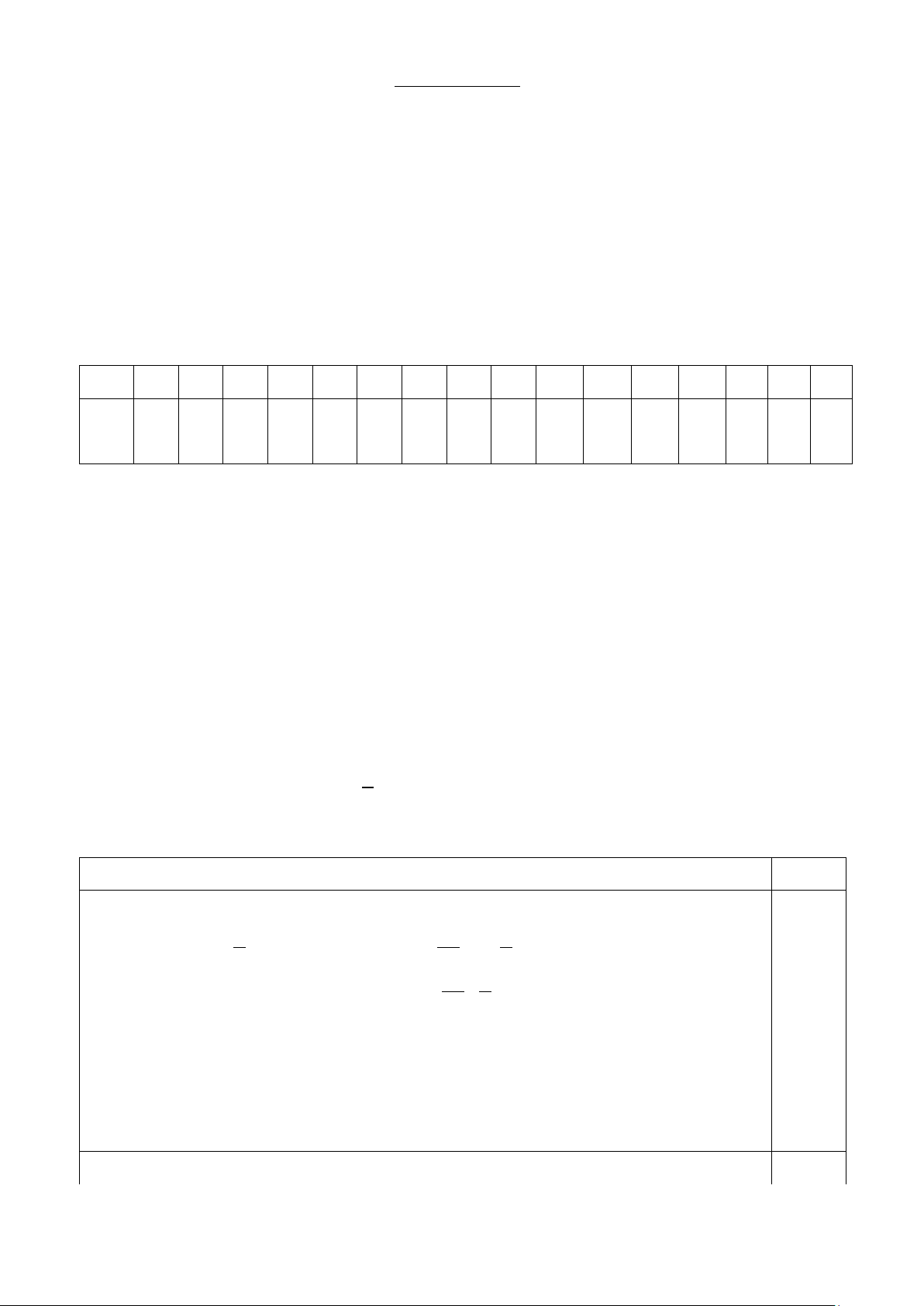
1) Cho hình vẽ bên: A
Hình thoi ABCD có chu vi là 120 cm. Tổng độ dài hai
đường chéo là 84cm, hiệu độ dài hai đường chéo là 12cm. D B
a) Tính độ dài hai đường chéo của hình thoi. H
b) Tính độ dài chiều cao AH. C
2) Cho 100 đường thẳng trong đó bất kỳ hai đường thẳng nào cũng cắt nhau và không có ba đường
thẳng nào cùng cắt nhau tại một điểm. Tìm số giao điểm được tạo thành. ....Hết....
Họ và tên thí sinh:.......................................SBD:..........
Cán bộ coi thi không cần giải thích gì thêm./. 3
TRƯỜNG TRUNG HỌC CƠ SỞ THANH THỦY
HƯỚNG DẪN CHẤM THI CHỌN HSNK LỚP 6, 7, 8 THCS – CẤP TRƯỜNG NĂM HỌC 2023 - 2024 MÔN: TOÁN 6
Hướng dẫn chấm có: 03 trang
A. Một số chú ý khi chấm bài.
Đáp án dưới đây dựa vào lời giải sơ lược của một cách giải. Thí sinh giải cách khác mà đúng
thì tổ chấm cho điểm từng phần ứng với thang điểm của hướng dẫn chấm.
B. Đáp án và thang điểm.
PHẦN I: TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN (4,0 điểm): Mỗi câu đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Đáp D A B C B B A A B D C B C B B C án
PHẦN II: TRẮC NGHIỆM ĐÚNG - SAI (2,0 điểm):
Điểm tối đa của mỗi câu là 1,0 điểm.
+ Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được: 0,1 điểm.
+ Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được: 0,25 điểm.
+ Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được: 0,5 điểm.
+ Thí sinh lựa chọn chính xác cả 04 ý trong 1 câu hỏi được: 1 điểm. Câu 1. A. Sai B. Đúng. C. Đúng. D. Đúng. Câu 2. A. Sai B. Đúng C. Sai D. Đúng
PHẦN III: TỰ LUẬN (14,0 điểm): Câu 1 (4,0 điểm).
a) Tìm số tự nhiên x, biết: 3x−2 1 5 5 5 + 3 .5 = 28,5.5 2
b) Tìm số nguyên tố p sao cho p + 6, p + 8, p +12, p + 24 cũng là các số nguyên tố. Gợi ý Điểm a) Ta có: 3x−2 1 5 5 3x−2 57 5 7 5 5 + 3 .5 = 28,5.5 0,5 ⇒ 5 = .5 − .5 2 2 2 3x−2 57 7 5 ⇒ 5 = ( − ). 2 5 2 0,5 3x−2 5 ⇒ 5 = 25.5 3x−2 7 ⇒ 5 = 5 0,5 ⇒ 3x − 2 = 7 ⇒ x = 3 Vậy x = 3 0,5
b) Với p = 2; p = 3 ta thấy không thỏa mãn yêu cầu bài toán 0,5 4 Với p = 5, ta có:
p + 6 = 5 + 6 =11; p + 8 = 5 + 8 =13; p +12 = 5 +12 =17; p + 24 = 5 + 24 = 29 0,5
đều là số nguyên tố (thỏa mãn)
Với p > 5, khi đó ta có các trường hợp của P là:
p = 5k +1; p = 5k + 2; p = 5k + 3; p = 5k + 4 (với *
k ∈  ) đều không thỏa mãn Vậy p = 5 1,0 Câu 2 (3,0 điểm). 6 4 9 5 4 . 9 . − 3 (.−8)4
a) Rút gọn biểu thức sau: C = 13 8 4 3 4 2 . 3 . + . 2 8 .( 27 − )
b) Tìm các số tự nhiên x, y, z nhỏ nhất khác không sao cho 24.x = 36.y = 54.z Gợi ý Điểm
a) 𝐶𝐶 = 5.46.94−39.(−8)4 = 5.46.94−39.84 = 5.212.38−39.212 4.213.38+2.84.(−27)3 4.213.38−2.84.273 215.38−213.39 1,5
= 212.38(5−3) = 212.38.2 = 1 213.38(22−3) 213.38
b) Đặt 24.x = 36.y = 54.z = m (với m ∈  *) ⇒ m  24; m  36; m  54 0,5
Do x, y, z nhỏ nhất khác không thỏa mãn 24x = 36y = 54z nên m cũng nhỏ nhất 0,5
mà m  24; m  36; m  54 ⇒ m = BCNN(24,36,54)
Ta tìm được BCNN(24,36,54) = 216⇒ m = 216
Với m = 216 ta tìm được x = 9; y = 6; z = 4 0,5
Vậy x = 9; y = 6; z = 4 Câu 3 (3,0 điểm)
a) Tính giá trị của các biểu thức sau: 1 1 1 1
1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) + … + (1 + 2 + … + 200). 2 3 4 200
b) Kỳ thi học sinh năng khiếu huyện Thanh Thủy năm học 2022- 2023 có 500 học sinh tham gia thuộc
các khối 6, 7, 8. Biết rằng số học sinh khối 6 có 30% tổng số học sinh dự thi và 10 số học sinh khối 7 17
bằng 5 số học sinh khối 8. Hỏi mỗi khối có bao nhiêu học sinh dự thi? 9 Gợi ý Điểm 1 1 n n +1 0,5 a) Ta có ( ) ( ) n +1 1+ 2 + 3+...+ n = . = n n 2 2 5 1 1 1 1
S = 1+ (1+ 2) + (1+ 2 + 3) + (1+ 2 + 3+ 4) +…+ (1+ 2 +…+ 200) Do đó, ta có: 2 3 4 200 3 4 5 201 = 1+ + + +. .+ 2 2 2 2 1 2 3 4 5 200 200 = + + + + +. .+ + 2 2 2 2 2 2 2 0,5 1 = (1+ 2 + 3+..+ 200) +100 2 1 200.(200 + ) 1 = . +100 2 2 = 10150 0,5
b) 20 tấn ứng với 100% − 75% = 25% (số thóc của ngày thứ ba).
Ngày thứ 3 đội vận chuyển được: 20 : 25% = 80 (tấn). 0,5
Suy ra, 80 + 20 =100 (tấn) ứng với: 5 4
1− = (số thóc còn lại sau ngày thứ nhất). 9 9
Số thóc còn lại sau ngày thứ nhất là: 4 100 : = 225 (tấn). 9 0,5
Do đó, 225 +15 = 240 (tấn) ứng với: 1 3
1− = (số thóc trong kho). 4 4 Vậy kho có số thóc là: 3 240 : = 320 (tấn). 0,5 4 Câu 4 (1,0 điểm)
Bình gieo hai con xúc xắc cùng lúc 50 lần. Ở mỗi lần gieo, Bình cộng số chấm xuất hiện ở hai con xúc
xắc và ghi lại kết quả như bảng sau: Tổng số chấm 2 3 4 5 6 7 8 9 10 11 12 Số lần 2 5 4 7 8 7 5 4 3 3 2
Tính xác suất thực nghiệm số lần xuất hiện tổng số chấm ở hai con xúc xắc lớn hơn 6. Gợi ý Điểm
Số lần Bình gieo được tổng số chấm lớn hơn 6 là: 0,5
7 + 5 + 4 + 3 + 3 + 2 = 24 (lần)
Xác suất thực nghiệm số lần xuất hiện tổng số chấm ở hai con xúc xắc lớn hơn 6 là: 0,5 24 : 50 = 12 25 Câu 5 (3,0 điểm) 6
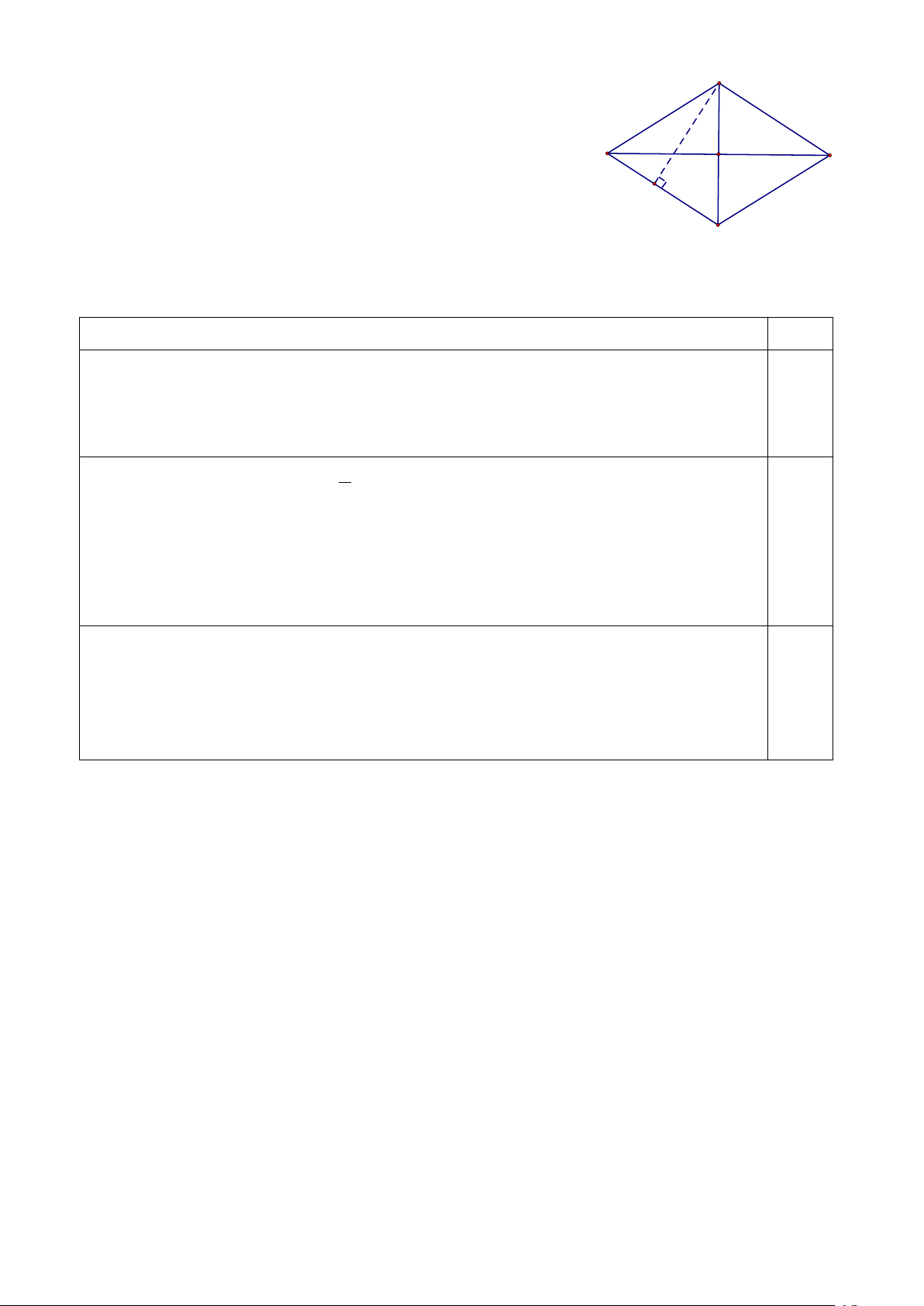
1) Cho hình vẽ bên: A
Hình thoi ABCD có chu vi là 120 cm. Tổng độ dài hai
đường chéo là 84cm, hiệu độ dài hai đường chéo là 12cm.
a) Tính độ dài hai đường chéo của hình thoi. D B
b) Tính độ dài chiều cao AH. H C
2) Cho 100 đường thẳng trong đó bất kỳ hai đường thẳng nào cũng cắt nhau và không có ba đường
thẳng nào cùng cắt nhau tại một điểm. Tìm số giao điểm được tạo thành. Gợi ý Điểm 1)
a) Độ dài đường chéo lớn của hình thoi là: (84 +12) : 2 = 48 (cm) 0,5
Độ dài đường chéo nhỏ của hình thoi là: 36 (cm) 0,5
b) Diện tích hình thoi là: 1 S = = cm 0,5 ABCD .48.36 864( 2 ) 2 Mặt khác S = AH CD ABCD .
Ta có cạnh hình thoi ABCD là 120:4 = 30 (cm) Do đó AH = S CD = = (cm) ABCD : 864 :30 28,8 0,5
2) Từ một đường thẳng kẻ cắt 99 đường thẳng còn lại tạo thành 99 giao điểm
Có 100 đường thẳng thì số giao điểm là: 100.99 ( giao điểm) 0,5
Tuy nhiên mỗi giao điểm đã được tính 2 lần, nên số giao điểm tạo thành là: 100.99:2 = 4950 giao điểm. 0,5
--------------- HẾT ------------- 7