Đề học sinh năng khiếu Toán 7 năm 2023 – 2024 phòng GD&ĐT Thanh Thủy – Phú Thọ

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO THANH THUỶ
ĐỀ THI CHỌN HỌC SINH NĂNG KHIẾU LỚP 6,7,8 THCS NĂM HỌC: 2023-2024 Đề chính thức MÔN: TOÁN LỚP 7
Thời gian làm bài: 120 phút, không kể thời gian giao đề. Đề thi có: 03 trang.
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (6,0 điểm)
1. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 16, mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Trong các số sau, số nào là số thập phân vô hạn tuần hoàn? A. 1 B. 1 C. 8 D. 7 16 15 16
Câu 2. Các hình khác nhau đại diện cho các số khác nhau. Hỏi hình vuông có giá trị bằng bao nhiêu? A. 8. B. 7. C. 6. D. 5.
Câu 3. Giả sử 4a 5; 5b 6; 6c 7; 7d = = = = 8. Hỏi tích a. .
b .cd bằng bao nhiêu? A. 1. B. 3 . C. 2. D. 5 . 2 2
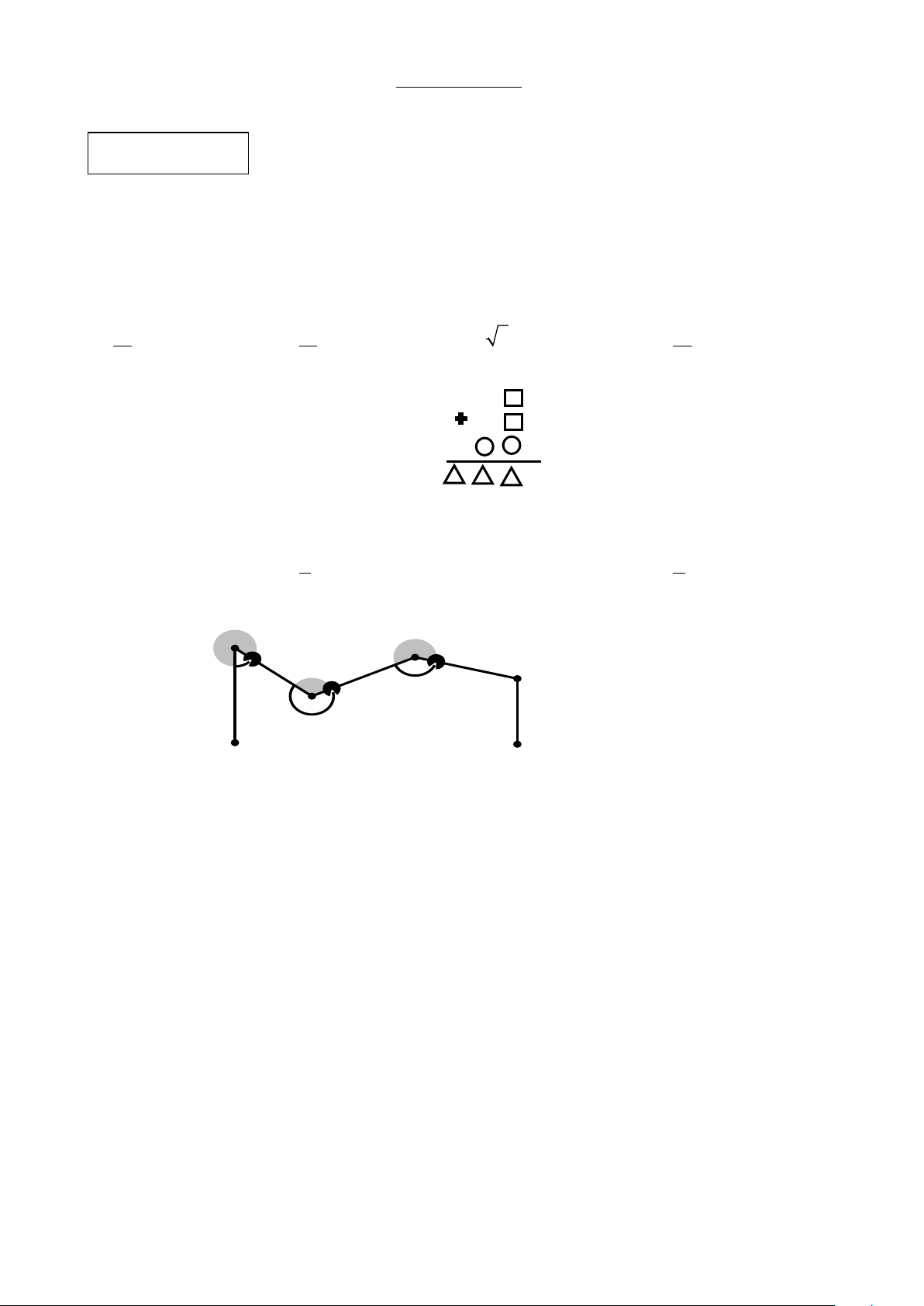
Câu 4. Cho hình vẽ, biết AB / /EF . Số đo  DEF bằng B D 60° E C 140° 230° A F A. 0 105 . B. 0 110 . C. 0 115 . D. 0 120 .
Câu 5. Cho tam giác ABC . Gọi M là trung điểm của BC , kẻ BH ⊥ AM , CK ⊥ AM ( H, K ∈ AM ).
Biết BH = 5cm . Khi đó độ dài đoạn CK là A. 2,5c . m B. 3c . m C.5c . m D. 6cm .
Câu 6. Cho tam giác ABC có AD là phân giác (D∈ BC), biết  
ADB : ADC = 4 :5. Đường trung trực
của BC cắt AC tại M. Tính số đo  ABM ? A. 0 20 . B. 0 30 C. 0 40 . D. 0 60 .
Câu 7. Để biểu diễn sự thay đổi của một đại lượng theo thời gian ta dùng
A. Biểu đồ hình quạt tròn. B. Biểu đồ cột kép. C. Biểu đồ tranh.
D. Biểu đồ đoạn thẳng.
Câu 8. Trong một nhóm gồm 50 học sinh, mỗi học sinh tham gia ít nhất một trong ba câu lạc bộ: Mỹ
thuật, Âm nhạc và khoa học.
Mọi học sinh tham gia câu lạc bộ âm nhạc đều tham gia câu lạc bộ mỹ thuật.
8 học sinh tham gia cả ba câu lạc bộ.
9 học sinh chỉ tham gia câu lạc bộ khoa học.
Có 20 học sinh trong câu lạc bộ âm nhạc
Có 18 học sinh trong câu lạc bộ khoa học
Hỏi có bao nhiêu học sinh chỉ tham gia duy nhất câu lạc bộ mỹ thuật? 1 A.16. B. 18. C. 19. D. 20.
Câu 9. Cho x, y là hai đại lượng tỉ lệ nghịch với nhau, x , x y , y 1
2 là hai giá trị của x ; 1 2 là hai giá trị
tương ứng của y . Biết x = 2; − y = 6 5x + 2y =12 x y 2 1 và 1 2 . Tính 1 và 2 . A. x = 12 − ; y = 36. x =12; y = 36. x = 3 − ; y =12. x = 4 − ; y =12. 1 2 B. 1 2 C. 1 2 D. 1 2
Câu 10. Cho 3a − 5b + 7c = 86 và a + 3 b − 2 c −1 = = khi đó 5 3 7
A. a = 7, b = 8, c =15 .
B. a = 8, b = 7, c =15 .
C. a =15, b = 8, c = 7. D. a = 7, − b = 8 − , c = 15. −
Câu 11. Cho đa thức P(x) = (x − 2)(x −1)x(x +1)(x + 2). Với giá trị nào của x thì P(x) nhận giá trị dương? A. 1,5. B. x = 1. − C. x = 0, − 5. D. x = 1, − 5.
Câu 12. Cho a, b thỏa mãn (x − )( 2 + ax + b) 3 2 3 2x
= 2x −8x + 9x − 9 với mọi x . Giá trị của a, b là A. a = 2,
− b = 3. B. a = 3,
− b = 2. C. a = 3, b = 2 − .
D. a = 2, b = 3.
Câu 13. Cho tam giác ABC với AB = AC = 7c .
m Chiều dài cạnh BC là một số nguyên và được tính
bằng cm. Hỏi chu vi tam giác ABC có thể lớn nhất bằng bao nhiêu? A. 15c . m B. 21c . m C. 25c . m D. 27c . m
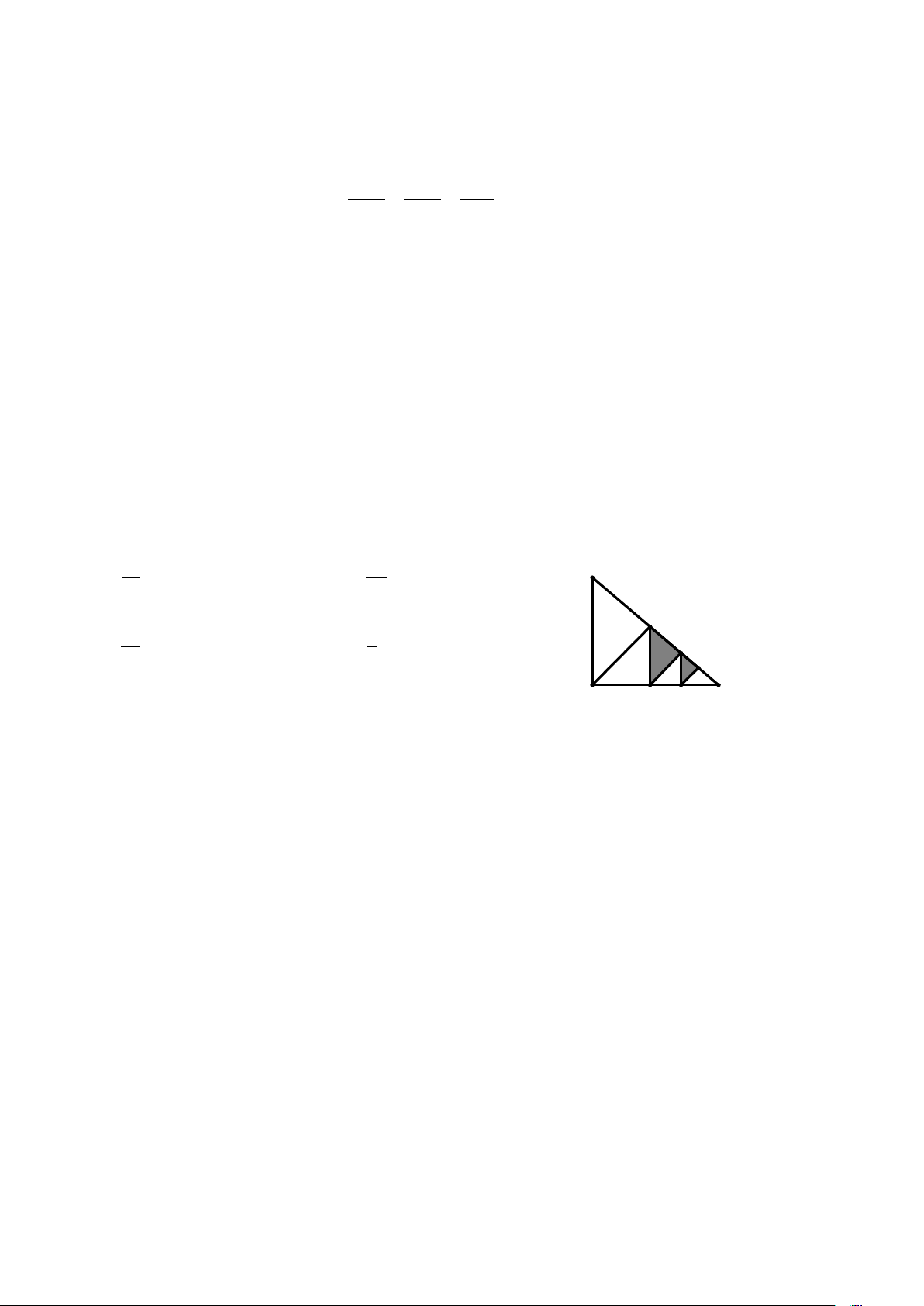
Câu 14. Cho tam giác PQR cân tại Q có QS,TU và VW lần lượt vuông góc với P ;
R ST và UV lần lượt vuông góc với .
QR (tham khảo hình vẽ). Tính tỉ số diện tích phần hình được tô đen so với diện tích tam giác P . QR A. 3 . B. 5 . P 16 32 S C. 5 . D. 3. U W 16 8 Q R T V
Câu 15. Anh Pi dùng các chữ số từ 1 đến 8, mỗi số chỉ dùng một lần để tạo ra hai số tự nhiên có 4 chữ
số. Hỏi tổng của hai số này lớn nhất bằng bao nhiêu? A. 16173. B. 15308. C. 13086. D. 6912.
Câu 16. Ba tổ công nhân A, B, C phải sản xuất cùng một số lượng sản phẩm như nhau. Thời gian ba tổ
hoàn thành kế hoạch theo thứ tự là 12 ngày, 15 ngày, 21 ngày. Tổ A nhiều hơn tổ C là 30 công nhân.
Hỏi tổ A nhiều hơn tổ B bao nhiêu công nhân?( Biết rằng năng suất lao động của các công nhân là như nhau). A. 10. B. 12. C. 14. D. 16.
2. Câu trắc nghiệm đúng sai. Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí
sinh trả lời đúng hoặc sai
Câu 1. Cho hai đa thức 3 2 (
A x) = x − x + ax + b − 2 và 2
B(x) = x − 2x + 3 ( với ; a b ∈ R ). a) Đa thức 2
B(x) = x − 2x + 3 vô nghiệm.
b) Với a =1; b =5 thì đa thức A(x) chia hết cho đa thức B(x). c) Khi (
A x) có nghiệm x = 0 thì b = 2 − .
d) Hệ số của x trong đa thức P(x) = (
A x) + B(x) là a − 2 .
Câu 2. Cho tam giác ABC vuông tại A có I là giao điểm ba đường phân giác của tam giác. Từ C kẻ
đường vuông góc với tia BI cắt tia BI tại H và cắt tia BA tại D. Khi đó a)  0 BIC =145 .
b) BH là đường trung tuyến của tam giác BCD .
c) Đường thẳng kẻ từ D đi qua giao điểm của BH và CA thì vuông góc với BC.
d) Tam giác BCD đều. 2
II. PHẦN TỰ LUẬN (14,0 điểm) Câu 1 (4,0 điểm).
1) Tính giá trị của các biểu thức sau: a)  6 15 47 1   17 5 1 A −  : 99 100  = + − − − +  13 26 39 78 65 52 130      1 5 7 + − b) x 4 8 13 B = + với 5 10 x ; y − = − = y 2 10 14 − − + 6 11 12 24 39
2) Cho a, b là hai số nguyên dương. Biết rằng trong 4 phát biểu sau có 3 phát biểu đúng và một phát biểu sai. a) (a + ) 1 chia hết cho b ; b) a = 2b + 5;
c) a + b là bội của 3;
d) a + 7b là số nguyên tố. Tìm a và . b Câu 2 (3,0 điểm). 1) Cho 2 2 b = ;
ac c = bd với ,
b c,d ≠ 0 và b + c + d ≠ 0 . Chứng minh rằng 3 3 3 3
a + b + c
 a + b + c  = 3 3 3 b c d   b c d  + + + + 
2) Cho đa thức P(x) thỏa mãn 2
P(x) + 3P(2) = 5x với mọi giá trị của x . a) Tính P(3).
b) Tìm nghiệm của đa thức P(x) − 5.
Câu 3 (4,0 điểm). Cho tam giác ABC vuông tại A, Bx là đường phân giác trong của 
ABC . Từ C hạ
đường vuông góc với Bx tại D . Gọi M là trung điểm của AC, DM cắt BC tại N. a) Chứng minh DA ∆ C cân.
b) Chứng minh N là trung điểm của BC.
c) Cho BD = AC . Tính số đo góc  ABC . Câu 4 (2,0 điểm).
Tính số các số tự nhiên có 4 chữ số đôi một khác nhau được thành lập từ các chữ số
0, 1, 2, 3, 4, 5 sao cho trong mỗi số đó đều có mặt ít nhất chữ số 1 hoặc 2.
Câu 5 (1,0 điểm). Gọi a ,a ,a ,....,a là các số tự nhiên thoả mãn: 1 2 3 100 1 1 1 1 199 + + + ...+ = . 2 2 2 2 a a a a 100 1 2 3 100
Chứng minh rằng ít nhất hai số tự nhiên trong các số trên bằng nhau. .....Hết....
Họ và tên thí sinh:.......................................SBD:..........
Cán bộ coi thi không cần giải thích gì thêm./. 3
PHÒNG GIÁO DỤC & ĐÀO TẠO THANH THỦY
HƯỚNG DẪN CHẤM THI CHỌN HỌC SINH NĂNG KHIẾU LỚP 6, 7, 8 THCS NĂM HỌC 2023 - 2024 MÔN: TOÁN 7
Hướng dẫn chấm có: 04 trang
A. Một số chú ý khi chấm bài
- Đáp án chấm thi dưới đây dựa vào lời giải sơ lược của một cách. Khi chấm thi giám khảo cần bám
sát yêu cầu trình bày lời giải đầy đủ, chi tiết, hợp logic và có thể chia nhỏ đến 0,25 điểm.
- Thí sinh làm bài theo cách khác với đáp mà đúng thì tổ chấm cần thống nhất cho điểm tương ứng
với thang điểm của đáp án.
- Điểm bài thi là tổng điểm các câu không làm tròn số.
B. Đáp án và thang điểm.
I. PHẦN TRẮC NGHIỆM (6,0 điểm)
1. Câu trắc nghiệm nhiều phương án lựa chọn (4,0 điểm).
Mỗi câu trả lời đúng cho 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Đáp án B C B B C A D D A A D A D B A C
2. Câu trắc nghiệm đúng sai (2,0 điểm)
Điểm tối đa của mỗi câu là 1,0 điểm.
+ Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được: 0,1 điểm.
+ Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được: 0,25 điểm.
+ Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được: 0,5 điểm.
+ Thí sinh lựa chọn chính xác cả 04 ý trong 1 câu hỏi được: 1 điểm. Ý a) b) c) d) Câu 1 Đúng Đúng Sai Đúng 2 Sai Đúng Đúng Sai
II. PHẦN TỰ LUẬN (14,0 điểm) Câu 1 (4,0 điểm).
1) Tính giá trị của các biểu thức sau: a)  6 15 47 1   17 5 1 A −  : 99 100  = + − − − +  13 26 39 78 65 52 130      1 5 7 + − b) x 4 8 13 B = + với 5 10 x ; y − = − = y 2 10 14 − − + 6 11 12 24 39
2) Cho a, b là hai số nguyên dương. Biết rằng trong 4 phát biểu sau có 3 phát biểu đúng và một phát biểu sai. a) (a + ) 1 chia hết cho b b) a = 2b + 5
c) a + b là bội của 3
d) a + 7b là số nguyên tố Tìm a và . b 4 Nội dung Điểm 1) 2,0 a)  6 15 47 1   17 5 1 A −  : 99 100  = + − − − +  13 26 39 78 65 52 130       36 − 45 94 1   34 1 5  : 99 100  = + − − + −  78 78 78 78 130 130 52      0,5  43 −   14 5  : 99 100  = −  39 52 52       43 −   9  43 −   52  4 0,5  :  1  = − +  =  . = 39 52         39   43 −  3 1 5 7 1 5 7 + − + − b) x 4 8 13 x 4 8 13 x 3 B = + = + = − y 2 10 14 y 2 −  1 5 7  y 2 0,5 − − + + − 12 24 39 3  4 8 13    Thay 5 10 x ; y − = − =
vào biểu thức B ta được 6 11 5 10 − 3 11 18 7 0,5 B − : − = − = − = 6 11 2 12 12 12 2) 2,0
Ta thấy c) a + b là bội của 3 là phát biểu sai. Vì nếu a + b là bội của 3 đúng thì
từ b) a = 2b + 5 ⇒ a + b = 3b + 5 3 ⇒ 53 (vô lí) 0,25
và từ d) a + 7b là số nguyên tố ⇒ a + b + 6b là số nguyên tố (vô lí do a + b + 6b3 và
a + b + 6b >3) 0,25
Từ a) và b) ta có 2b + 6b ⇒ 6b ⇒ b∈{1,2,3, } 6 0,5
Nếu b = 1 thì a = 7 khi đó a + 7b = 14 (loại)
Nếu b = 2 thì a = 9 khi đó a + 7b = 23 (T/m)
Nếu b = 3 thì a = 11 khi đó a + 7b = 32 (loại) 0,5
Nếu b = 6 thì a = 17 khi đó a + 7b = 59 (T/m)
Vậy có hai cặp giá trị: a = 9, b = 2 và a = 17, b = 6. 0,5 Câu 2 (3,0 điểm). 1) Cho 2 2 b = ;
ac c = bd với ,
b c,d ≠ 0 và b + c + d ≠ 0 . Chứng minh rằng 3 3 3 3
a + b + c
 a + b + c  = 3 3 3 b c d   b c d  + + + + 
2) Cho đa thức P(x) thỏa mãn 2
P(x) + 3P(2) = 5x với mọi giá trị của x . a) Tính P(3).
b) Tìm nghiệm của đa thức P(x) − 5. Nội dung Điểm 1) Cho 2 2 b = ;
ac c = bd với ,
b c,d ≠ 0 và b + c + d ≠ 0 . Chứng minh rằng 3 3 3 3
a + b + c
 a + b + c  = 1,5 3 3 3 b c d   b c d  + + + +  Từ 2 a b
b = ac ⇒ = và 2 b c
c = bd ⇒ = Suy ra a c b = = b c c d b d c 0,5
Theo t/c của DTSBN ta có: a c b a + b + c = = =
b d c b + c + d 5 3 3 3 3 a c b
 a + b + c  3 3 3 a + b + c 0,75 ⇒ = = = = 3 3 3 b d c   b c d  + +  3 3 3 b + d + c 3 3 3 3
Vậy a + b + c
 a + b + c  = 3 3 3 b c d  0,25  b c d  + + + + 
2) Cho đa thức P(x) thỏa mãn 2
P(x) + 3P(2) = 5x với mọi giá trị của x . a) Tính P(3).
b) Tìm nghiệm của đa thức P(x) − 5. 1,5 a) Vì 2
P(x) + 3P(2) = 5x với mọi giá trị của x nên 2
P(2) + 3P(2) = 5.2 ⇒ P(2) = 5 0,5 ⇒ 2
P(x) = 5x −15 ⇒ 2 P(3) = 5.3 −15 = 30 0,5 b) 2 2
P(x) − 5 = 0 ⇒ 5x − 20 = 0 ⇒ x = 4 ⇒ x = 2 ±
Vậy nghiệm của đa thức P(x) − 5là x = 2 ± 0,5
Câu 3 (4,0 điểm). Cho tam giác ABC vuông tại A, Bx là đường phân giác trong của 
ABC . Từ C hạ
đường vuông góc với Bx tại D . Gọi M là trung điểm của AC , DM cắt BC tại N. a) Chứng minh DA ∆ C cân.
b) Chứng minh N là trung điểm của BC.
c) Cho BD = AC . Tính số đo góc  ABC . Nội dung Điểm G A D M C B N
a) Chứng minh DA ∆ C cân. 1,5
Gọi G là giao điểm của CD và tia BA. 0,25 Chỉ ra được B ∆ DC = B ∆ DG(g. .
c g) ⇒ DC = DG ⇒ D là trung điểm của GC 0,5
Tam giác AGC vuông tại A có AD là đường trung tuyến ứng với cạnh huyền GC nên 1 AD 0,5 = GC = CD 2 A
∆ DC có DA = DC nên A ∆ DC cân tại D 0,25
b) Chứng minh N là trung điểm của BC 1,5 A
∆ DC cân tại D có DM là đường trung tuyến ⇒ DM cũng là đường trung trực ứng 0,25 với cạnh AC
Vì N ∈ DM nên NA = NC 0,25 ⇒ N
∆ AC cân tại N ⇒  =  NCA NAC 0,25 Lại có  +  0 =  +  0 = ⇒  = 
NCA ABN 90 ; NAC BAN 90 ABN BAN 0,25 N ∆ AB có  =  ABN BAN ⇒ N
∆ AB cân tại N ⇒ NA = NB 0,25 6
Suy ra NB = NC ⇒ N là trung điểm của BC 0,25
c) Cho BD = AC . Tính số đo góc  ABC 1,0 Chỉ ra được A ∆ BC = D
∆ CB(ch − cgv) 0,25 ⇒  =  1 =  DBC ACB ABC 0,25 2 A
∆ BC vuông tại A nên ta có  0,5 +  0 = ⇒  1 +  0 3 = ⇒  0 = ⇒  0 ABC ACB 90 ABC ABC 90 ABC 90 ABC = 60 2 2 Câu 4 (2,0 điểm).
Tính số các số tự nhiên có 4 chữ số đôi một khác nhau được thành lập từ các chữ số 0, 1, 2, 3, 4, 5 sao
cho trong mỗi số đó đều có mặt ít nhất chữ số 1 hoặc 2. Nội dung Điểm
Gọi các số cần tìm có dạng a a a a 1 2 3 4
+ Loại 1: Số tự nhiên có 4 chữ số tùy ý. 1,0
- Bước 1: Chọn 1 trong 5 chữ số khác 0 sắp vào a1 có 5 cách.
- Bước 2: Chọn 3 trong 5 chữ số khác a1 sắp vào 3 vị trí còn lại có 5.4.3  60 cách. Suy ra có 5.60 = 300 số.
+ Loại 2: Số tự nhiên có 4 chữ số gồm 0, 3, 4, 5 (không có 1 và 2).
- Bước 1: Chọn 1 trong 3 chữ số khác 0 sắp vào a1 có 3 cách.
- Bước 2: Sắp 3 chữ số còn lại vào 3 vị trí 3! = 6 cách. 1,0 Suy ra có 3.6 = 18 số.
Vậy có 300 – 18 = 282 số.
Câu 5 (1,0 điểm). Gọi a ,a ,a ,....,a là các số tự nhiên thoả mãn: 1 2 3 100 1 1 1 1 199 + + + ...+ = . 2 2 2 2 a a a a 100 1 2 3 100
Chứng minh rằng ít nhất hai số tự nhiên trong các số trên bằng nhau. Nội dung Điểm
Giả sử không có hai số nào bằng nhau trong các số a ,a ,a ,....,a 1 2 3 100
Từ giả thiết suy ra tất cả các số trên đều khác 0. Không mất tính tổng quát, giả sử :
1≤ a < a < a < .... < a . Suy ra: 0,25 1 2 3 100 1 1 1 1 1 1 1 1 + + + ...+ ≤ + + ...+ 2 2 2 2 2 2 2 2 a a a a 1 2 3 100 0,25 1 2 3 100 mà 1 1 1 1 1 1 1 1 199 + + ...+ < + + ...+ = 2 2 2 2 2 1 2 3 100 1 1.2 2.3 99.100 100 0,25 Suy ra 1 1 1 1 199 + + + ...+ <
, mâu thuẫn với giả thiết. Do vậy giả sử là sai 2 2 2 2 a a a a 100 1 2 3 100 0,25
Vậy ít nhất hai số tự nhiên trong các số trên bằng nhau 7