Đề HSG cấp trường Toán 10 năm 2020 – 2021 trường Yên Phong 2 – Bắc Ninh

Đề HSG cấp trường Toán 10 năm 2020 – 2021 trường Yên Phong 2 – Bắc Ninh gồm 01 trang với 04 bài toán dạng tự luận, thời gian làm bài 150 phút, đề thi có lời giải chi tiết và hướng dẫn chấm điểm, mời các bạn đón xem

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Họ và tên thí sinh: ……………………………………………….………. Số báo danh: ………………………..
Câu 1: (2,0 điểm)
Cho hàm số bậc hai
2
2( 1) 3 4
y x m x m
= − − − +
(1), với
m
là tham số.
a) Vẽ đồ thị hàm số (1) khi
2.
m
=
b) Tìm điểm cố định mà đồ thị hàm số (1)
luôn đi qua với mọi giá trị của
m
.
c) Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số (1)
cắt trục hoành tại hai điểm phân biệt
có hoành độ
,
x x
thỏa mãn
1 2
2 1
x x
− =
.
Câu 2: (3,0 điểm)
Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
, với
(
)
2; 3
A
,
(
)
2; 1
B
− −
,
(
)
1;5
C
.
a) Tìm tọa điểm
D
sao cho
4. 0
DA DB DC
− + =
  
.
b) Viết phương trình đường thẳng đi qua
D
và tạo với đường thẳng
AB
góc
45
°
.
c) Tính bán kính đường tròn ngoại tiếp tam giác
ABC
.
Câu 3: (3,0 điểm)
Giải hệ phương trình và bất phương trình sau đây:
a)
2 2
4 2 2
2 3 15
2 4 5
x y x y
x y x y
+ + =
+ − − =
.
b)
2
2 8 4 2
x x x
− + > −
.
Câu 4: (2,0 điểm)
Cho ba số thực
, , 0; 3 ,
x y z
∈
thỏa mãn
4
x y z
+ + =
. Tìm giá trị lớn nhất của biểu thức
(
)
2 2 2
3 2
P x y z xyz
= + + −
.
============= Hết =============
Thí sinh không được sử dụng tài liệu khi làm bài.
Cán bộ coi thi không giải thích gì thêm.
S
Ở GD
-
ĐT B
ẮC NINH
TRƯỜNG THPT YÊN PHONG SỐ 2
(Đề có 01 trang)
ĐỀ THI CHỌN HSG CẤP TRƯỜNG
NĂM HỌC 2020 – 2021
Môn: Toán – Lớp 10
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Thi ngày: 10/3/2021
Trang 1
SỞ GD-ĐT BẮC NINH
TRƯỜNG THPT YÊN PHONG SỐ 2
(HDC có 03 trang)
HƯỚNG DẪN CHẤM
KÌ THI CHỌN HSG CẤP TRƯỜNG
NĂM HỌC 2020 – 2021
Môn: Toán – Lớp 10
Lời giải sơ lược Điểm
Câu 1: (2,0 điểm)
a) Với
2
m
=
thì hàm số (1) trở thành
2
2 2
y x x
= − −
và có đồ thị như sau
x
y
1
3
1
- 1
- 3
- 2
O
1,0
b) Gọi
0 0
( ; )
M x y
là điểm cố định mà đồ thị hàm số (1)
luôn đi qua với mọi giá trị của
m
.
Ta có
2
0 0 0
2
0 0 0 0
0
0
2
0 0 0
0
2( 1) 3 4,
(2 3) ( 2 4) 0,
3
2 3 0
2
.
13
2 4 0
4
y x m x m m
m x y x x m
x
x
y x x
y
= − − − + ∀ ∈
⇔ + + − − − = ∀ ∈
= −
+ =
⇔ ⇔
− − − =
=
ℝ
ℝ
Vậy
3 13
( ; )
2 4
M −
là điểm cố định mà đồ thị hàm số (1)
luôn đi qua với mọi giá trị của
m
.
0,5
c) Phương trình
2
2( 1) 3 4 0
x m x m
− − − + =
có hai nghiệm phân biệt
,
x x
khi và chỉ
khi
2
1 13
' 3 0
2
m m m
− +
∆ = + − > ⇔ >
hoặc
1 13
(2).
2
m
− −
<
Lúc này, theo
định lí Viet, ta có
1 2 1 2
2( 1), 4 3 .
x x m x x m
+ = − = −
Nhận thấy
1 2
1 2
1 2
2( 1)
4 3 2 3
,
2 1
3 3
x x m
m m
x x
x x
+ = −
− −
⇔ = =
− =
, từ đây thế vào
Trang 2
1 2
4 3
x x m
= −
và biến đổi ta được
2
9 3 105
8 9 27 0
16
m m m
− ±
+ − = ⇔ = . Cả hai
giá trị này đều thỏa mãn (2). Vậy với
9 3 105
16
m
− ±
=
thì đồ thị hàm số (1)
cắt trục
hoành tại hai điểm phân biệt có hoành độ
,
x x
thỏa mãn
1 2
2 1
x x
− =
.
0,5
Câu 2: (3,0 điểm)
a) Gọi
0 0
( ; )
D x y
thì
0 0 0 0 0 0
(2 ;3 ), ( 2 ; 1 ), (1 ;5 ),
DA x y DB x y DC x y
= − − = − − − − = − −
  
0 0
4. (8 4 ;24 4 ).
DA DB DC x y
− + = − −
  
Do đó
0 0
0 0
8 4 0 2
4. 0 .
24 4 0 6
x x
DA DB DC
y y
− = =
− + = ⇔ ⇔
− = =
  
Vậy
(2;6).
D
1,0
b) Đường thẳng
d
đi qua điểm
(2;6)
D
, có một vectơ pháp tuyến
2 2
1
( ; ), 0.
n a b a b
= + ≠
Phương trình của
d
có dạng
( 2) ( 6) 0.
a x b y
− + − =
Vì
( 4; 4)
AB
= − −

nên
2
(1; 1)
n
= −
là một vectơ pháp tuyến của đường thẳng
.
AB
Ta có
1 2
2 2
1 2
.
0
2
cos 45 2a 0 .
0
2
.
2( )
n n a b
a
b
b
n n
a b
−
=
° = ⇔ = ⇔ − = ⇔
=
+
0,5
Nếu
0
a
=
thì
0
b
≠
nên
d
có phương trình
6 0.
y
− =
Nếu
0
b
=
thì
0
a
≠
nên
d
có phương trình
2 0.
x
− =
Vậy có 2 đường thẳng đi qua
D
và tạo với đường thẳng
AB
góc
0
45
có phương trình
lần lượt là
2 0, 6 0.
x y
− = − =
0,5
c) Với
(
)
2; 3
A
,
(
)
2; 1
B
− −
,
(
)
1;5
C
thì
4 2, 3 5, 5,
AB BC CA
= = =
1
( ) 2( 2 5).
2
p AB BC CA= + + = +
Diện tích tam giác
ABC
là
0,5
( ( )( ) 6.
S p p AB p BC p CA
= − − − =
Bán kính đường tròn ngoại tiếp tam giác
ABC
là
. . 5 2
4. 2
AB BC CA
R
S
= =
.
0,5
Câu 3: (3,0 điểm)
a)
2 2 2 2
4 2 2 2 2 4 2 2
2 3 15 2 3 15
2 4 5 2( 2 3 ) 2 4 35
x y x y x y x y
x y x y x y x y x y x y
+ + = + + =
⇔
+ − − = + + + + − − =
2 2
2 2
2
2 2 2
2
2 3 15
2 3 15
5
( ) 2( ) 35 0
7
x y x y
x y x y
x y
x y x y
x y
+ + =
+ + =
+ =
⇔ ⇔
+ + + − =
+ = −
2 2
2 2 2 2 2 2
2 2
2 2 2 2 4 2
5 5
0
(5 ) 2 3(5 ) 15 (4 ) 0 5
.
2
7 7
1
( 7 ) 2 3( 7 ) 15 8 36
y x y x
x
x x x x x x y
x
y x y x
y
x x x x x x
= − = −
=
− + + − = − = =
⇔ ⇔ ⇔
= ±
= − − = − −
=
− − + + − − = − − =
0,75
0,75
Trang 3
b)
2
2
2 2
2 8 4 0
2 0
2 2
2 8 4 2 .
4
2 8 4 ( 2)
2 0
x x
x
x
x x x
x
x x x
x
− + ≥
− <
≤ −
− + > − ⇔ ⇔
>
− + > −
− ≥
1,5
Câu 4: (2,0 điểm)
Vì
, , 0; 3 ,
x y z
∈
và
4
x y z
+ + =
nên
2 2 2 2 2 2
2 2 2 2
2 2 2 2
2 (3 )(3 )(3 ) 0
2 27 9( ) 3( ) 0
27 9.4 3( ) 0
6( ) 2 18
3( ) 6( ) 2 18 3( )
3( ) 2 18 3( )
3.4 2 18 3(
xyz x y z
xyz x y z xy yz zx xyz
xy yz zx xyz
xy yz zx xyz
x y z xy yz zx xyz x y z
x y z xyz x y z
xyz x y z
+ − − − ≥
⇔ + − + + + + + − ≥
⇔ − + + + + ≥
⇔ + + + ≥
⇔ + + + + + + ≥ + + +
⇔ + + + ≥ + + +
⇔ + ≥ + + +
2 2 2
)
3( ) 2 30.
x y z xyz
⇔ + + − ≤
1,0
0,5
Dấu “=” xảy ra khi trong ba số
, ,
x y z
có một số bằng 0, một số bằng 1 và một số bằng 3.
Vậy
(
)
{
}
2 2 2
max max 3 2 30.
P x y z xyz= + + − =
0,5
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD-ĐT BẮC NINH
ĐỀ THI CHỌN HSG CẤP TRƯỜNG
TRƯỜNG THPT YÊN PHONG SỐ 2
NĂM HỌC 2020 – 2021
Môn: Toán – Lớp 10
(Đề có 01 trang)
Thời gian làm bài: 150 phút (không kể thời gian giao đề) Thi ngày: 10/3/2021
Họ và tên thí sinh: ……………………………………………….………. Số báo danh: ……………………….. Câu 1: (2,0 điểm) Cho hàm số bậc hai 2
y = x − 2(m − 1)x − 3m + 4 (1), với m là tham số.
a) Vẽ đồ thị hàm số (1) khi m = 2.
b) Tìm điểm cố định mà đồ thị hàm số (1) luôn đi qua với mọi giá trị của m .
c) Tìm tất cả các giá trị của tham số m để đồ thị hàm số (1) cắt trục hoành tại hai điểm phân biệt
có hoành độ x , x thỏa mãn x − 2x = 1 . 1 2 1 2 Câu 2: (3,0 điểm)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC , với A(2; 3), B ( 2 − ;− ) 1 , C (1;5) .
a) Tìm tọa điểm D sao cho DA − DB + 4.DC = 0 .
b) Viết phương trình đường thẳng đi qua D và tạo với đường thẳng AB góc 45° .
c) Tính bán kính đường tròn ngoại tiếp tam giác ABC . Câu 3: (3,0 điểm)
Giải hệ phương trình và bất phương trình sau đây: 2 2 x
 y + 2x + 3y = 15 a)   . 4 2 2 x
+ y − 2x − 4y = 5  b) 2
2x − 8x + 4 > x − 2 . Câu 4: (2,0 điểm) Cho ba số thực x, , y z 0;3 ∈ , 
x + y + z =   thỏa mãn
4 . Tìm giá trị lớn nhất của biểu thức P = ( 2 2 2
3 x + y + z ) − 2xyz .
============= Hết =============
Thí sinh không được sử dụng tài liệu khi làm bài.
Cán bộ coi thi không giải thích gì thêm. SỞ GD-ĐT BẮC NINH HƯỚNG DẪN CHẤM
TRƯỜNG THPT YÊN PHONG SỐ 2
KÌ THI CHỌN HSG CẤP TRƯỜNG
NĂM HỌC 2020 – 2021
(HDC có 03 trang)
Môn: Toán – Lớp 10
Lời giải sơ lược Điểm Câu 1: (2,0 điểm)
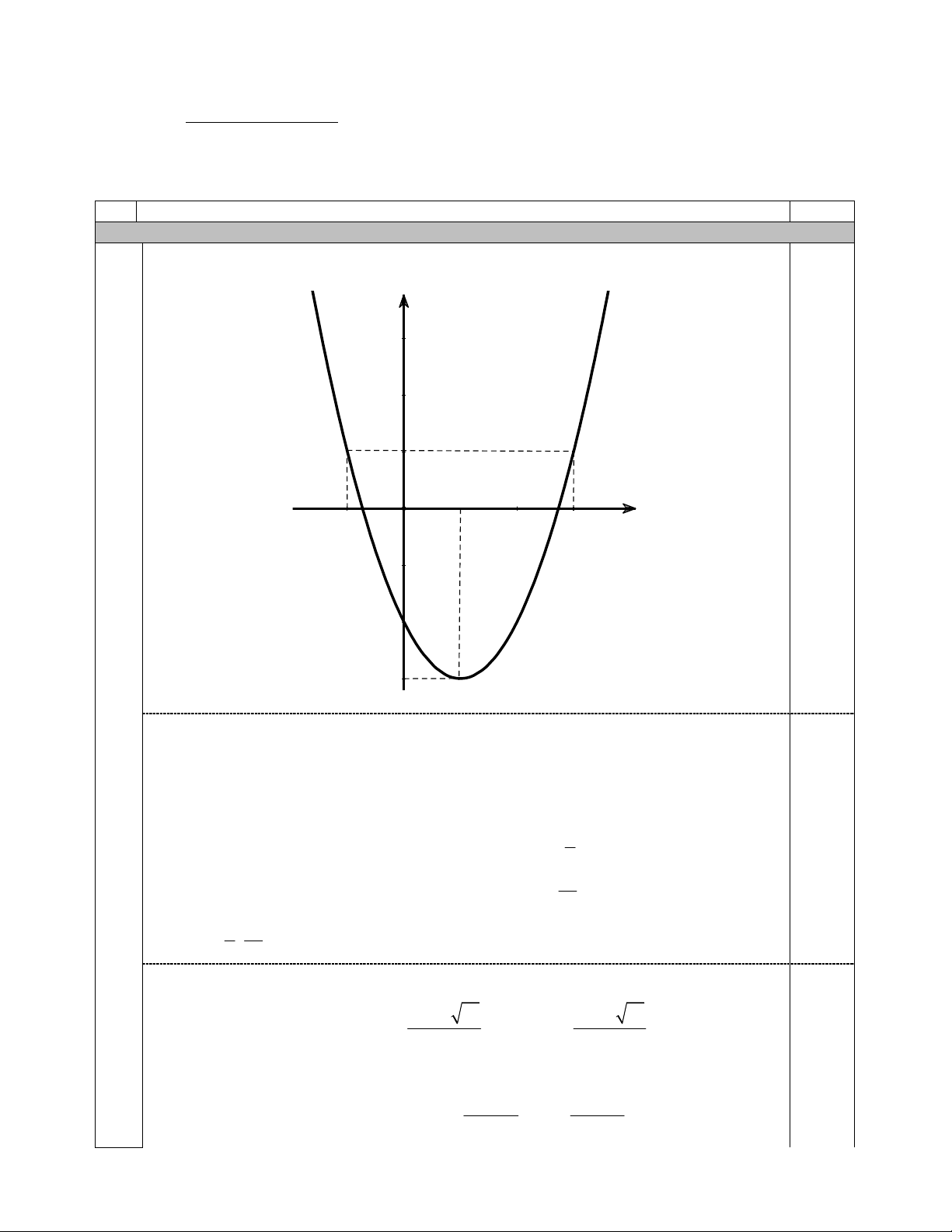
a) Với m = 2 thì hàm số (1) trở thành 2
y = x − 2x − 2 và có đồ thị như sau y 1 1,0 1 3 - 1 x O - 2 - 3
b) Gọi M(x ;y ) là điểm cố định mà đồ thị hàm số (1) 0 0
luôn đi qua với mọi giá trị của m . Ta có 2
y = x − 2(m − 1)x − 3m + 4, m ∀ ∈ ℝ 0 0 0 2 ⇔ (
m 2x + 3) + (y − x − 2x − 4) = 0, m ∀ ∈ ℝ 0 0 0 0  3  0,5 2  + 3 = 0 x x  = − 0  0   2 ⇔  ⇔  . 2 y
− x − 2x − 4 = 0  13  0 0 0  y  = 0  4 3 13 Vậy M(− ;
) là điểm cố định mà đồ thị hàm số (1) luôn đi qua với mọi giá trị của m . 2 4 c) Phương trình 2
x − 2(m − 1)x − 3m + 4 = 0 có hai nghiệm phân biệt x , x khi và chỉ 1 2 − + 1 − − 13 khi 2 1 13
∆ ' = m + m − 3 > 0 ⇔ m > hoặc m < (2). Lúc này, theo 2 2 đị
nh lí Viet, ta có x + x = 2(m − 1), x x = 4 − 3m. 1 2 1 2 x
 + x = 2(m −1)  4m − 3 2m − 3 Nhận thấy 1 2  ⇔ x = , x = , từ đây thế vào 1 2 x  − 2x = 1 3 3  1 2  Trang 1 − ±
x x = 4 − 3m và biến đổi ta được 2 9 3 105
8m + 9m − 27 = 0 ⇔ m = . Cả hai 1 2 16 −9 ± 3 105 0,5
giá trị này đều thỏa mãn (2). Vậy với m =
thì đồ thị hàm số (1) cắt trục 16
hoành tại hai điểm phân biệt có hoành độ x , x thỏa mãn x − 2x = 1 . 1 2 1 2 Câu 2: (3,0 điểm)
a) Gọi D(x ;y ) thì DA = (2 − x ;3 − y ),DB = ( 2 − − x ; 1
− − y ),DC = (1 − x ;5 − y ), 0 0 0 0 0 0 0 0
DA − DB + 4.DC = (8 − 4x ;24 − 4y ). Do đó 0 0  1,0 8 − 4x = 0 x  = 2  0  0
DA − DB + 4.DC = 0 ⇔  ⇔  . 2  4 − 4y = 0 y  = 6  0   0  Vậy D(2; 6).
b) Đường thẳng d đi qua điểm D(2;6), có một vectơ pháp tuyến 2 2
n = (a;b), a + b ≠ 0. 1
Phương trình của d có dạng a(x − 2) + ( b y − 6) = 0.
Vì AB = (−4;−4) nên n = (1;−1) là một vectơ pháp tuyến của đường thẳng AB. 0,5 2 n .n 2 a − b a  = 0 Ta có 1 2 cos 45 2ab 0  ° = ⇔ = ⇔ − = ⇔ .  2 2 n . n 2 b = 0 1 2 2(a + b ) 
Nếu a = 0 thì b ≠ 0 nên d có phương trình y − 6 = 0.
Nếu b = 0 thì a ≠ 0 nên d có phương trình x − 2 = 0. 0,5
Vậy có 2 đường thẳng đi qua D và tạo với đường thẳng AB góc 0 45 có phương trình
lần lượt là x − 2 = 0, y − 6 = 0.
c) Với A(2;3), B (−2;− )
1 , C (1;5) thì AB = 4 2,BC = 3 5,CA = 5, 1 0,5 p =
(AB + BC +C )
A = 2( 2 + 5). Diện tích tam giác ABC là 2 S = (
p p − AB(p − BC )(p −C ) A = 6. 0,5 AB.BC .CA 5 2
Bán kính đường tròn ngoại tiếp tam giác ABC là R = = . 4.S 2 Câu 3: (3,0 điểm) 2 2 2 2 x
 y + 2x + 3y = 15 x
 y + 2x + 3y = 15 a)    ⇔  4 2 2 2 2 4 2 2 x
+ y − 2x − 4y = 5 2
 (x y + 2x + 3y) + x + y − 2x − 4y = 35     2 2 x
 y + 2x + 3y = 15 2 2  x
 y + 2x + 3y = 15    2  ⇔ 
⇔  x + y = 5 2 2 2
(x + y) + 2(x + y) − 35 = 0    0,75   2   x + y = −7    2   2 y  = 5 − x y  = 5 − xx  = 0          2 2 2 2  2 2  x
(5 − x ) + 2x + 3(5 − x ) = 15 x   (4 − x ) = 0    y  = 5        ⇔  ⇔  ⇔  . 0,75 2 2  y  = −7 − xy  = −7 − xx  = ±2          2 2 2 2 4 2  x  ( 7
− − x ) + 2x + 3(−7 − x ) = 15  x − − 8x = 36 y   = 1            Trang 2  2 2
 x − 8x + 4 ≥ 0  x 2 0   − <  x  ≤ 2 − 2 b)   2
2x − 8x + 4 > x − 2 ⇔  ⇔ . 1,5 2 2  2 
x − 8x + 4 > (x − 2) x   > 4      x  − 2 ≥ 0    Câu 4: (2,0 điểm)
Vì x,y, z 0;3 ∈ , 
và x + y + z = 4 nên  
2xyz + (3 − x)(3 − y)(3 − z) ≥ 0
⇔ 2xyz + 27 − 9(x + y + z) + 3(xy + yz + zx) − xyz ≥ 0
⇔ 27 − 9.4 + 3(xy + yz + zx) + xyz ≥ 0
⇔ 6(xy + yz + zx) + 2xyz ≥ 18 1,0 2 2 2 2 2 2
⇔ 3(x + y + z ) + 6(xy + yz + zx) + 2xyz ≥ 18 + 3(x + y + z ) 2 2 2 2
⇔ 3(x + y + z) + 2xyz ≥ 18 + 3(x + y + z ) 2 2 2 2
⇔ 3.4 + 2xyz ≥ 18 + 3(x + y + z ) 2 2 2
⇔ 3(x + y + z ) − 2xyz ≤ 30. 0,5
Dấu “=” xảy ra khi trong ba số x, ,
y z có một số bằng 0, một số bằng 1 và một số bằng 3. 0,5 Vậy P = { ( 2 2 2 max
max 3 x + y + z ) − 2xyz} = 30. Trang 3