Đề HSG Toán 10 năm 2023 – 2024 cụm trường THPT Gia Lâm & Long Biên – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CỤM LỚP 10
CỤM TRƯỜNG THPT GL - LB
NĂM HỌC 2023 - 2024 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
(Đề thi có 01 trang)
Bài I (4,0 điểm) Cho hàm số 2
y  2x  3x  5   1 .
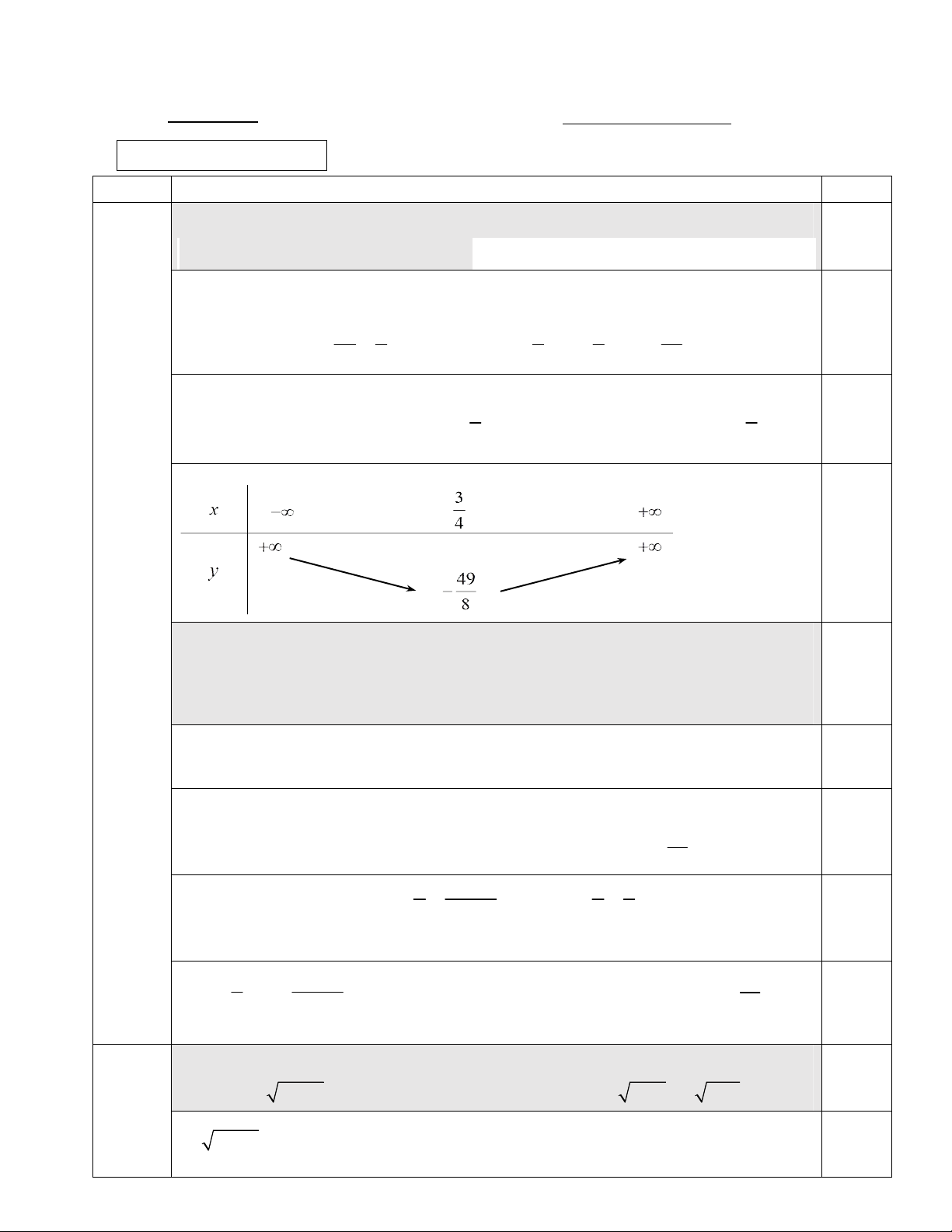
1) Lập bảng biến thiên của hàm số   1 .
2) Tìm các giá trị của tham số m để đồ thị của hàm số  
1 cắt đường thẳng y  4x  m tại hai
điểm phân biệt A x ; y , B  x ; y thỏa mãn 2 2
2x  2x  3x x  7 . 2 2  1 1  1 2 1 2 Bài II (6,0 điểm)
1) Giải các phương trình sau: a)
4x  5  2x  3. b) 2
x  2x  2x x  3  6 1 x  7.
2) Một công ty điện tử sản suất hai loại máy tính trên hai dây chuyền độc lập (loại một và loại
hai). Máy tính loại một sản xuất trên dây chuyền một với công suất tối đa 45 máy tính một ngày;
máy tính loại hai sản xuất trên dây chuyền hai với công suất tối đa 80 máy tính một ngày. Để sản
xuất một chiếc máy tính loại một cần 12 linh kiện và cần 9 linh kiện để sản xuất một máy tính loại
hai. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900 linh kiện và tiền lãi bán một
chiếc máy loại một là 2.500.000 đồng; tiền lãi khi bán một chiếc máy loại hai là 1.800.000 đồng.
Hỏi trong một ngày công ty cần sản xuất mỗi loại bao nhiêu máy tính để tiền lãi thu được là nhiều
nhất. (Giả thiết rằng tất cả các máy tính sản xuất ra trong ngày đều bán hết).
Bài III (3,0 điểm) Cho tam giác ABC đều có cạnh bằng .
a Gọi D là điểm trên cạnh BC sao cho  2   2  BD 
BC và I là trung điểm của AD . Gọi E là điểm thoả mãn AE  AC . 3 5 1) Chứng minh ba điểm ,
B I, E là ba điểm thẳng hàng.
2) M là điểm tùy ý thuộc miền trong tam giác ABC . Tìm giá trị nhỏ nhất của biểu thức
    
P  2MA  MB  MC  MB  MC .
Bài IV (5,0 điểm) Trong mặt phẳng tọa độ Oxy , cho hai điểm A2; 4 và B 8;4 .   
1) Tìm tọa độ điểm M thỏa mãn MA  2MB  0.
2) Tìm tọa độ điểm C thuộc trục hoành sao cho tam giác ABC vuông tại C .
3) Viết phương trình đường thẳng d song song với  : 3x  4 y  20  0 và cách điểm A(2; 4) một khoảng bằng 2. sin B  sin C
Bài V (2,0 điểm) Cho tam giác ABC thỏa mãn
 sin A và A .
B AC  12 . Gọi M cos B  cos C
là trung điểm của cạnh BC và G là trọng tâm của tam giác ABC . Tìm diện tích tam giác MBG .
- - - - - - - - - - Hết - - - - - - - - - -
Họ và tên thí sinh:...............................................Số báo danh:.........................................
Chữ kí CBCT 1: ......................................... Chữ kí CBCT 2: ..........................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CỤM LỚP 10
CỤM TRƯỜNG THPT GL - LB
NĂM HỌC 2023 - 2024
Môn thi: TOÁN HƯỚNG DẪN CHẤM Bài Nội dung Điểm Cho hàm số 2
y  2x  3x  5   1 . 2,0
1) Lập bảng biến thiên của hàm số   1 .
Tập xác định: D   . 0,5
Các hệ số: a  2 , b  3 , c  5 . 2 b 3  3  3 49
Tọa độ đỉnh: x    , y  y x      . Đ  Đ  2. 3. 5 Đ   2a 4  4  4 8
Vì a  2  0 nên ta có 0,5  3   3 
Hàm số nghịch biến trên khoảng ; ; 
 Hàm số đồng biến trên khoảng ;      4   4  Bảng biến thiên 1,0 Bài I (4,0 đ)
2) Tìm các giá trị của tham số m để đồ thị của hàm số   1 cắt đường thẳng
y  4x  m tại hai điểm phân biệt
A x ; y ,
B  x ; y thỏa mãn 2 2  1 1  2,0 2 2
2x  2x  3x x  7 . 1 2 1 2
Phương trình hoành độ giao điểm của đồ thị hàm số   1 với đường thẳng 0,5
d  : y  4x  m : 2
2x  3x  5  4x  m 2
 2x  7x  5  m  0 2 Đồ thị hàm số  
1 và đường thẳng d  cắt nhau tại hai điểm phân biệt khi và chỉ khi 0,5 89
phương trình 2 có nghiệm phân biệt x , x    0  m   . 1 2 8 c 5  m b 7 0,5
Theo hệ thức Vi-et, có: x .x  
, x  x    . 1 2 a 2 1 2 a 2 Khi đó 2 2
2x  2x  3x x  7  2 x  x  7x x  7  0 1 2 2 1 2 1 2 1 2 2 0,5  7  5  m 89  2.  7.  7  0  
 7m  70  0  m  10 (thỏa mãn m   )  2  2 8
Vậy m  10 thỏa mãn yêu cầu bài toán.
3) Giải các phương trình 4,0 c)
4x  5  2x  3. b) 2
x  2x  2x x  3  6 1 x  7. Bài II 0,5 (6,0 đ) 2 x  3  0 
a) 4x  5  2x  3  
4 x  5  2x  32   3 1,0 x   2   
x  2  3 n 
x  2  3 l 
Vậy phương trình có nghiệm x  2  3 . 0,5 x  3  0,5 b) 2
x  2x  2x x  3  6 1 x  7 . ĐKXĐ:  . y  1  Đưa về phương trình 2
x  2x x  3  x  3  1 x  2. 1 x.3  9
 x  x  3  1 x  3   1 0,5
 x  x  2    x  2 3 1 3    x 
x  3   1 x  3 2 
+) Với x  x  3  1 x  3. Giải ra được x  1 0,5
+) Với x  x  3   1 x  3  x  3  x  3  1 x  0 (vô nghiệm vì 0,5
3  x  1). Vậy hệ phương trình có nghiệm duy nhất: x  1 .
4) Một công ty điện tử sản suất hai loại máy tính trên hai dây chuyền độc lập … 2,0 Gọi ,
x y  x, y   lần lượt là số máy tính loại 1 và loại 2 cần sản xuất tra trong 0,5 0  x  45 
một ngày. Theo đề bài ta có: 0  y  80 (*) 1
 2x  9y  900  0,5
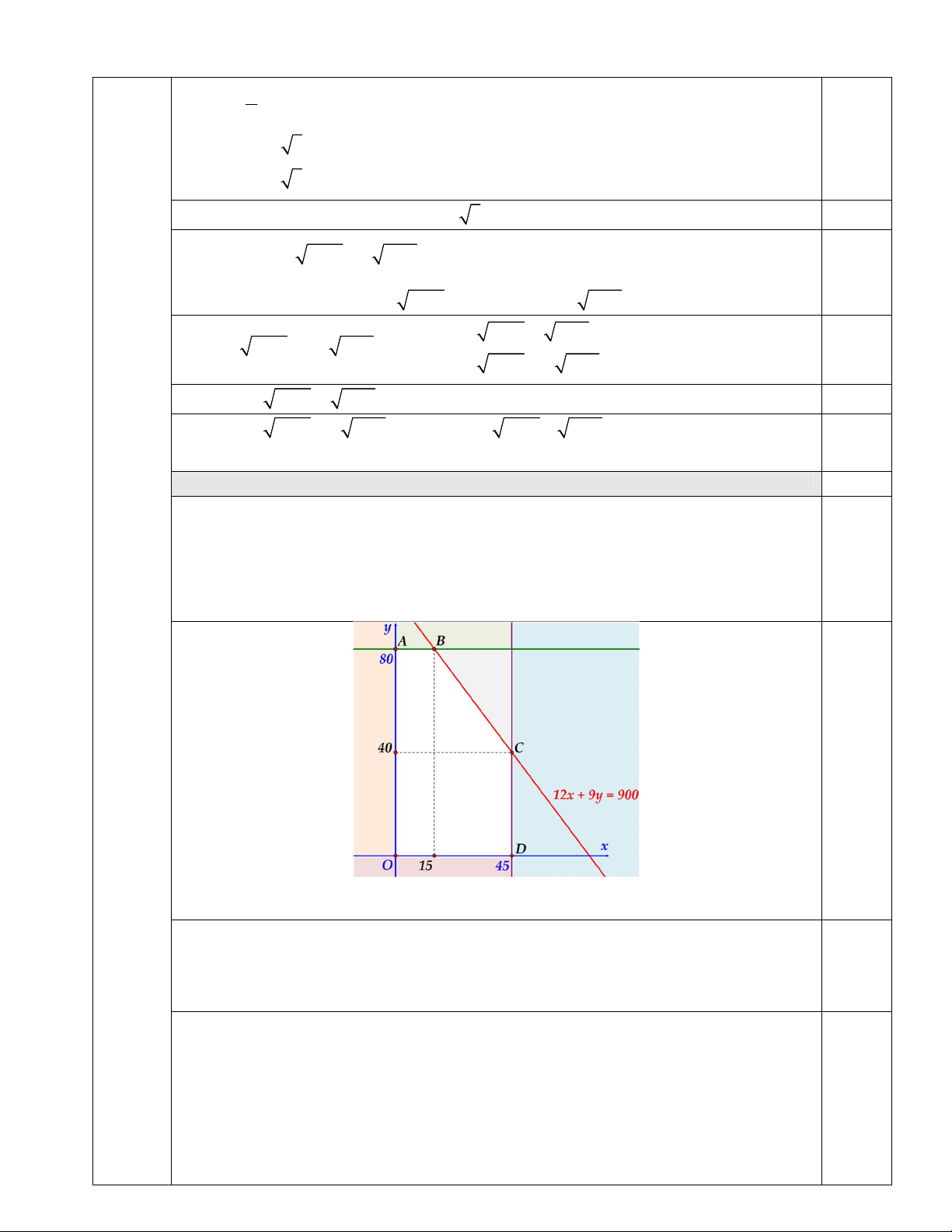
Miền nghiệm của bất phương trình là miền ngũ giác OABCD với các đỉnh 0,5
O 0;0, A0;80, B 15;80,C 45;40, D 45;0 .
Gọi F là số tiền lãi thu được, ta có: F  x y 6 6 ,
 2,5.10 x 1,8.10 y .
Tính giá trị của F tại các đỉnh của ngũ giác ta có: 0,5
Tại O 0;0 : F 0;0  0 . Tại A0;80 : F   6 0;80  144.10 .
Tại B 15;80 : F   6
15;80  181, 5.10 . Tại C 45;40 : F   6 45; 40  184, 5.10 .
Tại D 45;0 : F   6 45;0  112,5.10 .
Vậy công ty cần sản xuất 45 máy tính loại 1 và 40 máy tính loại 2 để có lãi cao nhất là 184.500.000 đồng. 2,0
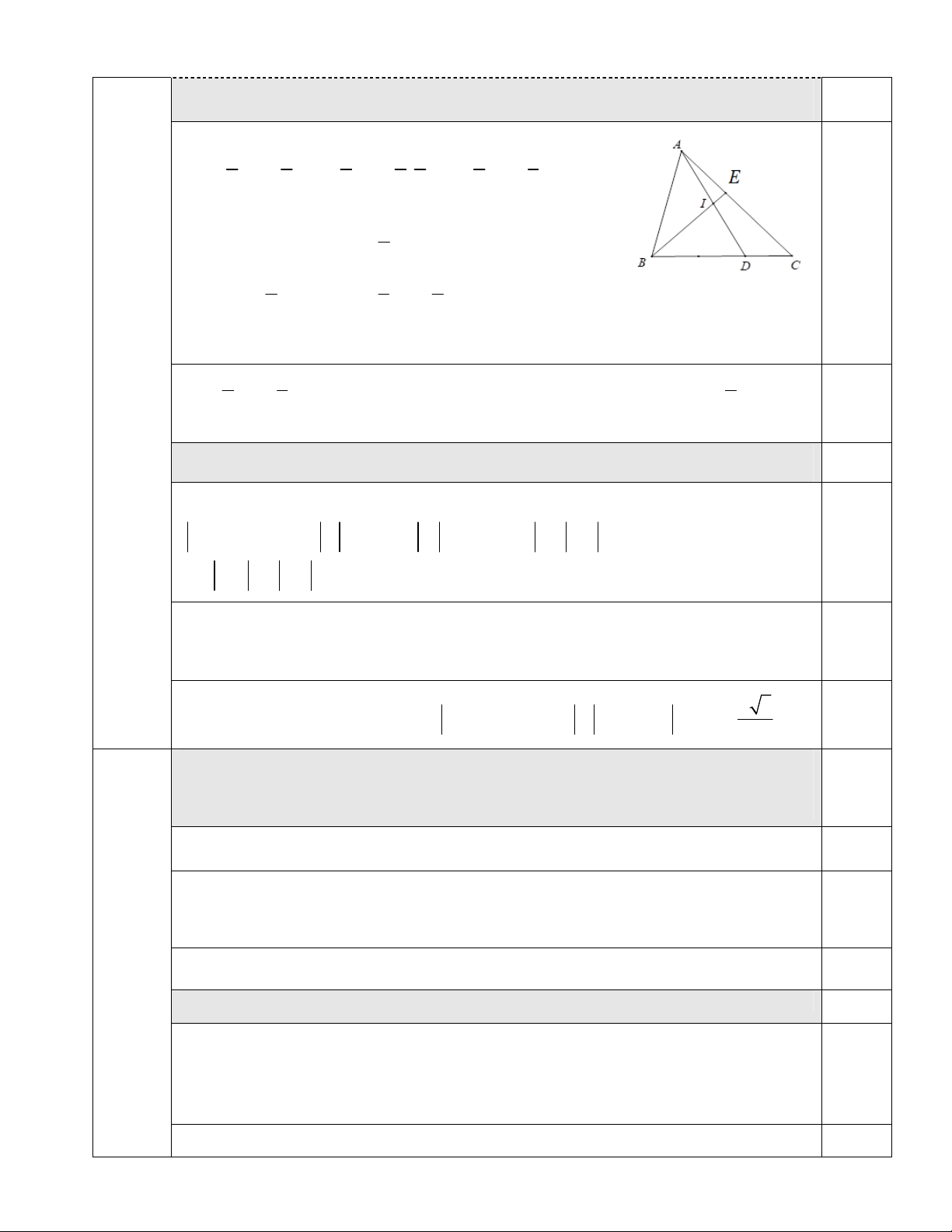
1) Cho tam giác ABC đều cạnh ,
a …Chứng minh ba điểm ,
B I, E thẳng hàng. Ta có: 1,0
 1  1  1  1 2  1  1  BI  BA  BD  BA  . BC  BA  BC . 2 2 2 2 3 2 3 Ta lại có:
    2 
BE  BA  AE  BA  AC 5
 2    
 BA  BC  BA 3 2  BA  BC. 5 5 5   
Hay 5BE  3BA  2BC .
 1  1        5  1,0 Bài III BI 
BA  BC hay 6BI  3BA 2BC . Do đó: 6BI  5BE hay BI  BE . 2 3 6 (3,0 đ) Vậy ,
B I, E thẳng hàng. 1,0
2) M là điểm tùy ý thuộc miền trong tam giác ABC . Tìm giá trị nhỏ nhất …
Gọi P là trung điểm đoạn BC và là Q trung điểm đoạn A . P Khi đó 0,5
       
2MA  MB  MC  MB  MC  2MA  2MP  2 MP  
 4 MQ  2 MP  4MQ  2M . P
Ta có 2MQ  2MP  2PQ (dấu đẳng thức xảy ra khi và chỉ khi M thuộc đoạn PQ ) 0,25
và 2MQ  0 .(dấu đẳng thức xảy ra khi và chỉ khi M  Q ).
Suy ra 2MQ  2EM  2MP  2PQ  AP .
     0,25 a 3
Vậy giá trị nhỏ nhất của biểu thức 2MA  MB  MC  MB  MC  AP  . 2 2,0
Trong mặt phẳng tọa độ Oxy , cho hai điểm A2; 4 và B 8;4 .   
1) Tìm tọa độ điểm M thỏa mãn MA  2MB  0.   Gọi M  ;
x y  , ta có: MA  2  x; 4  y  , MB  8  x; 4  y  . 0,5       2   x  2 1,0  8  x x  18
Từ giả thiết, suy ra: MA  2MB  0  MA  2MB     . 4  y  2  4  y y  4   Bài IV (5,0 đ)
Vậy điểm cần tìm: M 18;4 . 0,5
2) Tìm tọa độ điểm C thuộc trục hoành sao cho tam giác ABC vuông tại C . 1,0
Điểm C thuộc trục hoành nên có tọa độ dạng C  ; c 0 . 0,5  
Ta có: CA  2  c; 4 , CB  8  c; 4 .    
Tam giác ABC vuông tại C nên CA  CB  CA  CB  C . A CB  0
 c  8c  2 16  0 2
 c  6c  0  c  0 hoặc c  6 . 0,5
Vậy có hai điểm C cần tìm là C 0;0 và C 6;0 .
3) Viết phương trình đường thẳng d song song với  : 3x  4 y  20  0 … 2,0 Ta có:
d / / : 3x  4 y  20  0  Phương trình d có dạng: 1,0
3x  4 y  c  0, c  20.
| 3.2  4.4  c | Mặt khác: d ( , A d )  2   2 |  10  c | 10 9 16 c  0 1,0 
 d : 3x  4 y  0.  (Vì c  20 ). c  20  sin B  sin C 2,0
Cho tam giác ABC thỏa mãn A . B AC  12 và  sin A … cos B  cos C
Đặt BC  a, AC  b, AB  c . 0,5
Áp dụng định lí sin cho A  BC ta có: a b c sin A  ,sin B  ,sin C  2R 2R 2R Bài V 0,5 (2,0 đ) sin B  sin C Khi đó
 sin A  b  c  a cos B  cosC  (*) cos B  cos C
Áp dụng định lí cosin cho A  BC ta có (*) 0,5 2 2 2 2 2 2
 a  c  b
a  b  c 
 b  c  a  2 2 2 
  c  b b  c  a   0 2ac 2ab   A . B AC 0,5 2 2 2
 b  c  a  tam giác ABC vuông tại A và S   6 . ABC 2 1 1 Ta có S  S  S  1. GBM 2 GBC 6 ABC
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.