Đề khảo sát đội tuyển Toán 10 lần 2 năm 2021 – 2022 trường THPT Trần Phú – Vĩnh Phúc

MA TRẬN ĐỀ KHẢO SÁT ĐỘI TUYỂN LẦN 2
TOÁN 10- NĂM HỌC 2021-2022 CẤP ĐỘ TƯ DUY TỔNG VẬN DỤNG NỘI DUNG NHẬN BiẾT THÔNG HiỂU VẬN DỤNG CAO TL TL TL TL Câu 1, câu 2 Hàm số 2 2 Câu 3 Hệ pt 1 ẩn 1 1 ĐẠI PT và HPT quy Câu 4a Câu 4b, câu 5 về bậc nhất , bâc 2 1 2 3 Câu 9 Bất đẳng thức 1 1 Vec tơ Câu 6 Câu 7 1 1 2 HÌNH Hệ thức lượng Câu 8 trong tam giác 1 1 Tổng 5 3 2 SỞ GD & ĐT VĨNH PHÚC
ĐỀ KHẢO SÁT ĐỘI TUYỂN TOÁN LẦN 2
TRƯỜNG THPT TRẦN PHÚ
Năm học: 2021 - 2022
Môn: Toán – Lớp 10
Thời gian làm bài: 180 phút, không kể thời gian phát đề
Câu 1: (1 điểm) Cho Parabol P 2
: y  x  2x  2 và đường thẳng d  : y  2
 x 1. Biết P và d  cắt nhau tại
hai điểm phân biệt A và B . Tính độ dài đoạn AB 1
Câu 2: (1 điểm) Tìm tập xác định của hàm số y  . 2 4x 19x 12 2
x  5x  4  0
Câu 3: (1 điểm) Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm.
x  m  0
Câu 4: (2 điểm) a) Giải phương trình 2
x  3 + x  2 = x  3x  2 2 3 2
ìïx + x y- xy + xy- y =1 b)
Giải hệ phương trình: ïí 4 2
ïx + y - xy(2x- ) 1 =1 ïî
Câu 5: (1 điểm) Gọi x ; x 2 1
2 là hai nghiệm của phương trình x  mx  m  1  0 . 4x x  6 Đặt 1 2 A 
. Tìm giá trị của tham số m để A đạt giá trị nhỏ nhất. 2 2 x  x  1 ( 2  x x ) 1 2 1 2
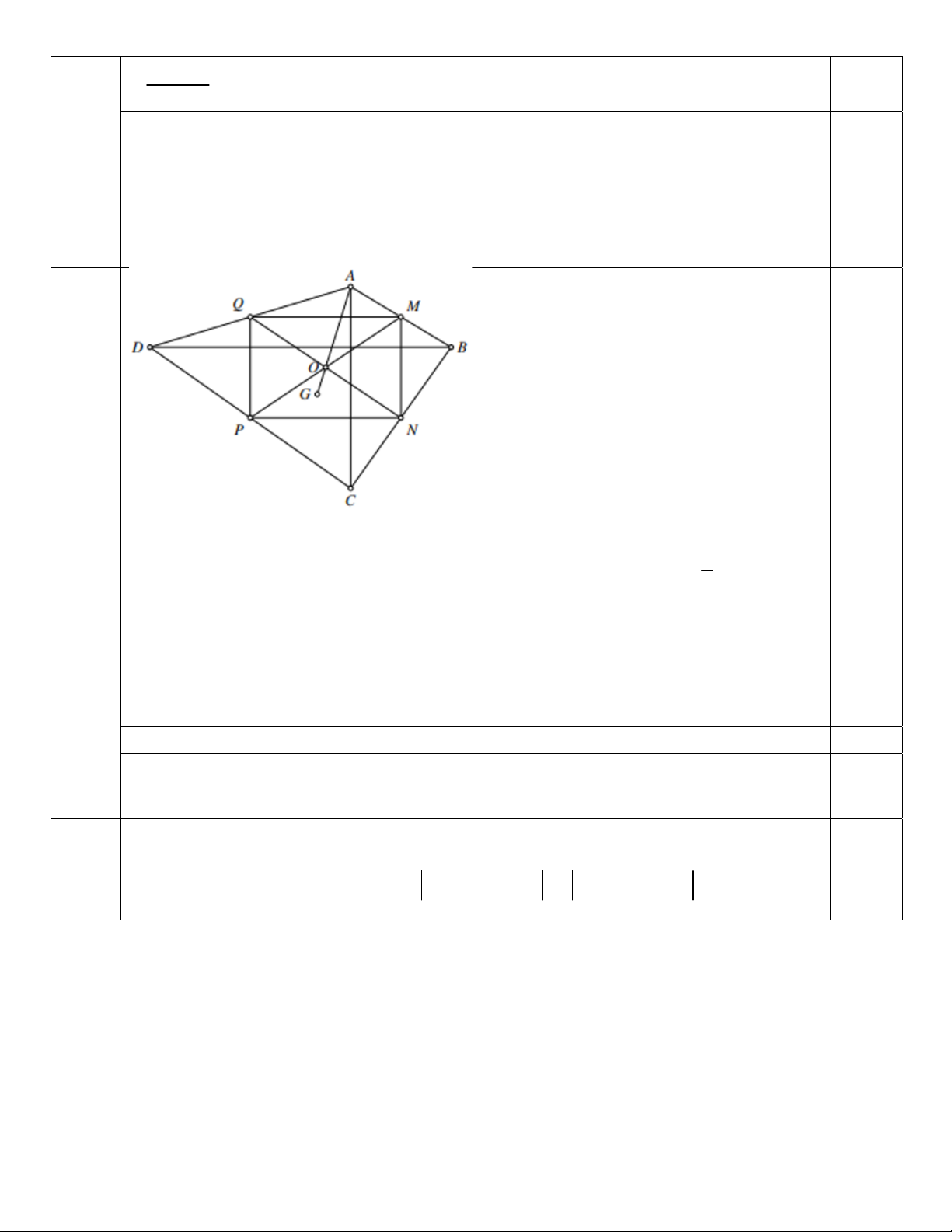
Câu 6: (1 điểm) Cho tứ giác ABCD . Gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , DA . Gọi
O là giao điểm của MP và NQ , G là trọng tâm của tam giác BCD . Chứng minh rằng ba điểm A ,
O , G thẳng hàng.
Câu 7: (1 điểm) Cho tam giác ABC là tam giác đều cạnh bằng a , M là điểm di động trên đường thẳng AC .
  
  
Tìm giá trị nhỏ nhất của biểu thức T  MA  MB  MC  3 MA  MB  MC .
Câu 8: (1 điểm) Cho tứ giác lồi ABCD có AC  BD và nội tiếp đường tròn tâm O bán kính R  1010 . Đặt
diện tích tứ giác ABCD bằng S và AB  a, BC  b,CD  c, DA  d . Tính giá trị biểu thức
ab  cdad bc T  . 4S
Câu 9: (1 điểm) Cho x, y là các số thực thay đổi. Tìm giá trị nhỏ nhất của biểu thức A x   
 y  x  2 2 2 1
1  y  y  2 ------------HẾT------------
Họ và tên thí sinh..................................................................................................SBD.......................................... SỞ GD & ĐT VĨNH PHÚC HƯỚNG DẪN CHẤM
TRƯỜNG THPT TRẦN PHÚ
ĐỀ KHẢO SÁT ĐỘI TUYỂN TOÁN LẦN 2
Năm học: 2021 - 2022
Môn: Toán – Lớp 10
(Hướng dẫn chấm gồm 6 trang) Câu Nội dung Điểm
Câu 1 Cho Parabol P 2
: y  x  2x  2 và đường thẳng d  : y  2
 x 1. Biết P và d  cắt nhau 1 điểm
tại hai điểm phân biệt A và B . Tính độ dài đoạn AB x  1 
Phương trình hoành độ giao điểm: 2 2
x  2x  2  2x 1  x  4x  3  0   x  3  0,5  A 1  ;  1 ; B  3
 ;5 . Ta có AB  2 5 0,5 Câu 2 1
Tìm tập xác định của hàm số y  . 1 điểm 2 4x 19x 12  x  4 1 Hàm số y 
xác định khi và chỉ khi 2
4x 19x 12  0  2 3 4x 19x 12 x   4 0,5  x  4  3    3  D   ;   4;    0,5 x   4   4 Câu 3 2
x  5x  4  0
Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm.
x  m  0 1 điểm 2     1   x  4 x x   1 5 4 0 Ta có     0,5 x  m  0 x  m  2
Để hệ bất phương trình có nghiệm thì giao hai tập nghiệm của hai bất phương trình   1 , 2 0,5
khác rỗng  m  4
Câu 4 a) Giải phương trình 2
x  3 + x  2 = x  3x  2 1 điểm Đk x  3 PT 2 2
 x  3 x  2  2 x  5x  6  x  3x  2 2 2
 x  5x  6  2 x  5x  6  3  0 0,25 Đặt 2
t  x  5x 
6, t  0. Ta được pt : 2
t  2t  3  0 0,25 t  1(l 2
 t  2t  3  0   t  3(n) 0,25 2 2
t  3  x  5x  6  3  x  5x  3  0  5  37 x  (l) 5  37 2
. KL pt có nghiệm là x    2 0,25  5  37 x  (n)  2 2 3 2
ìïx + x y- xy + xy- y =1
b)Giải hệ phương trình: ïí 1 điểm 4 2
ïx + y - xy(2x- ) 1 =1 ïî ì 2 2 2 3 2
ìïx + x y- xy + xy - y =1 (1) (ïx - y ï
)+ xy(x - y)+ xy =1 + Ta có: ïí ( ) * ï  í 4 2
ïx + y - xy(2x- ) 1 = 1 (2) 2 ïî (ï 2
ï x - y) + xy =1 ïî 0,25 2 a ìï = x - y
ìïa + ab +b =1 + Đặt ïí . Hệ trở thành ïí ( ) ** b ï = xy 2 ïî ïa +b =1 ïî ì 3 2
ïïa + a -2a = 0 ìïa ï ï ( 2 a + a - ) 2 = 0 + Hệ (**)  í  í 2 ï = - ï 2 b 1 a ï b ï =1- a ïî î 0,25
Từ đó ta tìm ra (a ) b Î ( ; { 0 ) ( ; 1 ; 1; ) ( 0 ; 2 - ;- ) 3 } 2 ìïx - y = 0 Với ( ; a b)=( 0; ) 1 ta có hệ ïí  x = y =1 ïxy =1 ïî 0,25 2 ìïx - y =1  Với ( ; a b)=( 1; ) 0 ta có hệ ïí  ( ; x y)= ( 0;- ) 1 ;(1; ) ( 0 ; 1 - ; ) 0 ïxy = 0 ïî Với ( ; a b)= ( 2 - ;- ) 3 ta có hệ   3  3 2 x  y  2  y   y       x  x   x  1  ; y  3 . xy  3  3 
x  2x  3  0 (x 1)   
 2x  x3  0 0,25
Vậy hệ có 5 nghiệm  ; x y  { 1;  1 ;0;  1 ;1; 0 : 1  ; 0; 1  ;  3 }.
Câu 5 Gọi x ; x 2 1
2 là hai nghiệm của phương trình x  mx  m  1  0 . 4x x  6 Đặt 1 2 A 
. Với giá trị nào của m thì A đạt giá trị nhỏ nhất. 2 2 x  x  1 ( 2  x x ) 1 2 1 2
+ PT có hai ngiệm khi   0  m2  4m  4  , 0 m
 ; x  x  ; m x x  m 1 1 2 1 2 0,25 4x x  6 4m  2 1 2 A   2 2 (x  x )  2 m  2 0,25 1 2 2 (m  2)  1  1  0,25 2 m  2
A nhỏ nhất khi m  2  0,25 Câu
Cho tứ giác ABCD . Gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , DA . Gọi 6
O là giao điểm của MP và NQ , G là trọng tâm của tam giác BCD . Chứng minh rằng ba
điểm A , O , G thẳng hàng. 0,25
MN // PQ // AC 
MN , PQ lần lượt là đường trung bình của ABC  , AC  D   1
MN  PQ  AC  2
Do đó tứ giác MNPQ là hình bình hành  O là trung điểm của MP .
           
Ta có: OA  OB  OC  OD  OM  MA  OM  MB  OP  PC  OP  PD    0,25
 2OM OP  0.
   
G là trọng tâm BC 
D  OB  OC  OD  3OG . 0,25
         
Khi đó: OA  OB  OC  OD  0  OA  3OG  0  OA   3OG .
Vậy ba điểm A , O , G thẳng hàng (đpcm). 0,25 Câu
Cho tam giác ABC là tam giác đều cạnh bằng a , M là điểm di động trên đường thẳng AC 7
  
   1 điểm
Tìm giá trị nhỏ nhất của biểu thức T  MA  MB  MC  3 MA  MB  MC . 0,25
Gọi G là trọng tâm ABC  thì G cố định.  
Vẽ CD  BA , vì ABC 
đều nên tứ giác ABCD là hình thoi và D cố định.
Khi đó ta có         
T  MA  MB  MC  3 MA  MB  MC  3 MG  3 BA  MC   
 3MG  3 CD  MC  3MG  3 MD  3MG  MD  3G . D 0,25
Do MG không đổi nên T đạt giá trị nhỏ nhất bằng 3GD khi M ,G, D thẳng hàng. Khi đó,
M là trung điểm đoạn AC . 0,25
Giá trị nhỏ nhất của T là 1 4 4 a 3 2a 3
3GD  GM  MD  GM  MB  MB  MB  MB  .  . 0,25 3 3 3 2 3
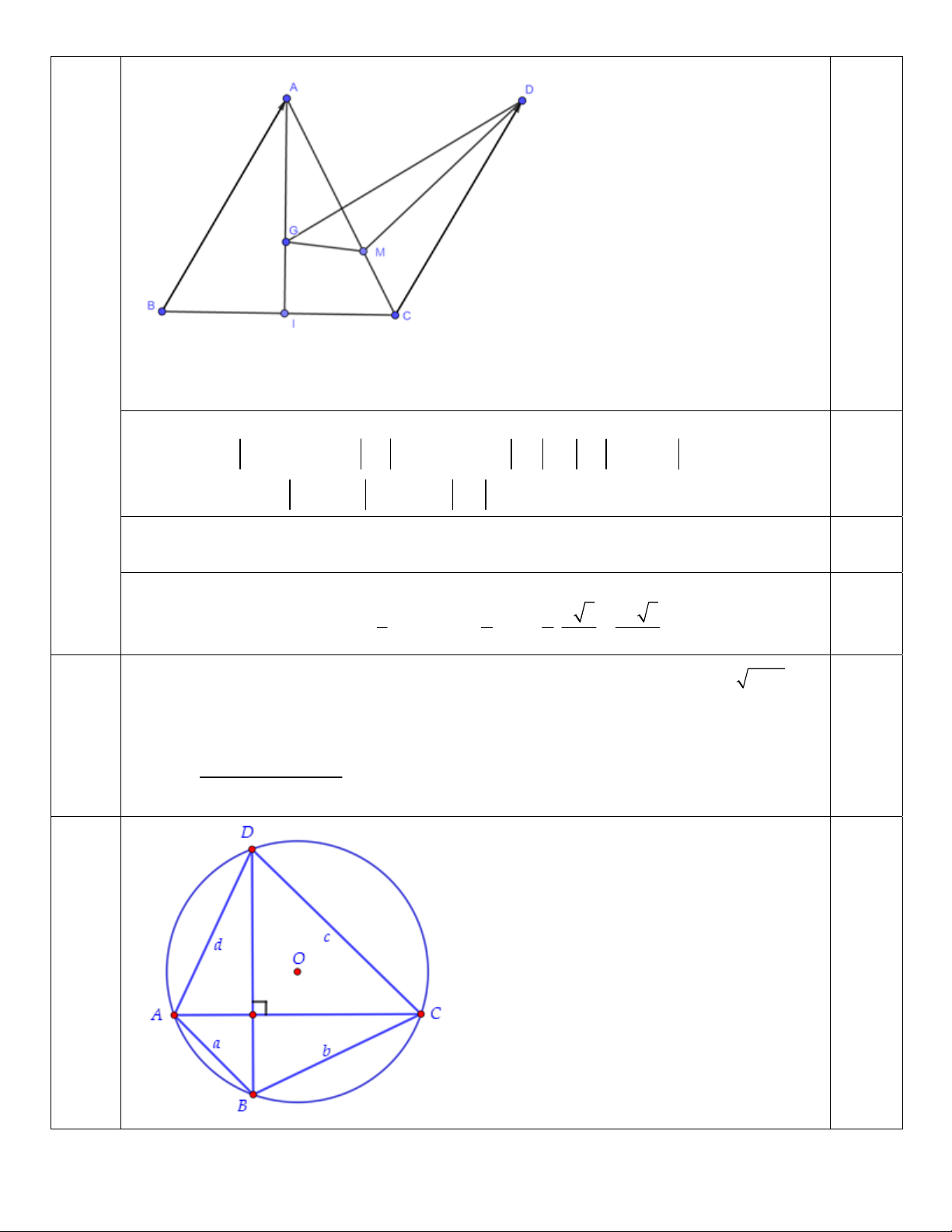
Câu 8 Cho tứ giác lồi ABCDcó AC  BD và nội tiếp đường tròn tâm O bán kính R  1010 .
Đặt diện tích tứ giác ABCD bằng S và AB  a, BC  b,CD  c, DA  d . Tính giá trị biểu 1 điểm
ab  cdad bc thức T  . 4S 0,25 . a . b AC S .4R Ta có : ABC S   ab  ABC 4R AC S .4R S .4R S .4R Tương tự ta cũng có : ADC cd  , ABD ad  , BCD bc  AC BD BD
ab  cdad bc T  . 4S  S .4R S .4R  S .4R S .4R  ABC ADC ABD BCD       AC AC  BD BD   . 0,25 4S 2 4R S .S  S .S  S .S  S .S ABC ABD ABC BCD ADC ABD ADC BCD   . S.AC.BD 4040 S S  S  S S  S   ABC  ABD BCD  ADC  ABD BCD   . 0,25 S.AC.BD
4040S .S  S .S S S  S ABC ADC
 4040  ABC ADC  4040S.S     2020 . S.AC.BD S.AC.BD S.2S 0,25 Vậy T  2020 .
Câu 9 Cho x, y là các số thực thay đổi. Tìm giá trị nhỏ nhất của biểu thức 1 điểm A x   
 y  x  2 2 2 1
1  y  y  2
A   x  2  y   x  2  y  y     x  x  2   y  y2 2 2 1 1 2 1 1  y  2 0,25 Vậy 2
A  4  4y  y  2 TH1: 2
y  2  A  2 1 y  2 5 0,25 TH2: 2
y  2  A  2 1 y  2  y 0,25   2 2   2 2 3 1
1  y   2  y  3.11.y  2  y  3  2 1
A  2  3 khi và chỉ khi x  0, y  3 0,25
Ta có 2  3  2 5  min A  2  3
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.