Đề khảo sát HSG Toán 8 năm 2023 – 2024 phòng GD&ĐT Văn Lâm – Hưng Yên

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI KHẢO SÁT HỌC SINH GIỎI HUYỆN VĂN LÂM
NĂM HỌC: 2023 – 2024
Môn: Toán – Lớp 8 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Đề thi gồm có 01 trang) Ngày thi: 04/4/2024
Bài 1. (4,0 điểm) Cho biểu thức: 2 2 2 2  −   − +  x y 2 1 1 2 1 x y 2xy 3 A = + : ( + ) . − + 
( x ≠ ±y ; ;x y ≠ 0) 2 2  2 2  x 2xy y
xy x y  x y (x y)(x y) x 2x 2 + + − − + − + 
1) Rút gọn biểu thức A.
2) Với giá trị nào của x, y thì biểu thức A đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Bài 2. (4,0 điểm)
1) Phân tích đa thức P = bc(a + d)(b − c) − ac(b + d)(a − c) + ab(c + d)(a − b)thành nhân tử.
2) Cho các số nguyên a, , b c thoả mãn 3 3 3
(a − b) + (b − c) + (c − a) = 210 . Tính giá trị của
biểu thức A = a − b + b − c + c − a .
Bài 3. (3,0 điểm)
1) Tìm số tự nhiên n để B = n3 – n2 – 7n + 10 là số nguyên tố.
2) Giải phương trình: (x – 3)3 + (2x – 1)3 = (3x – 4)3
Bài 4. (7,0 điểm)
1) Cho hình vuông ABCD . Gọi E là một điểm trên cạnh BC . Qua A kẻ tia Ax vuông góc với
AE và cắt CD tại F . Trung tuyến AI của tam giác AEF cắt CD ở K . Đường thẳng qua E
song song với AB cắt AI ở G . Chứng minh rằng:
a) AE = AF và tứ giác EGFK là hình thoi. b) 2
AF = FK.FC
c) Cho hình vuông ABCD cố định có độ dài cạnh bằng a , chứng minh rằng khi E di
động trên cạnh BC thì chu vi E ∆ KC không đổi.
2) Cho tam giác MNP có MN = 5cm, MP = 6cm, NP = 7cm. Gọi I là giao điểm của ba đường
phân giác, G là trọng tâm của tam giác MNP. Chứng minh rằng: IG//MP
Bài 5. (2,0 điểm)
1) Tìm hàm số có đồ thị là đường thẳng (d) thỏa mãn: (d) đường trung trực của AB và A(0; -1); B(-4; 3) 1 1 1
2) Chứng minh rằng: Nếu xyz = 1 thì + + =1
1+ x + xy 1+ y + yz 1+ z + zx
--------- Hết ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………………………..Số báo danh:……………….
Đáp án và thang điểm
Bài 1 (4,0 điểm). Cho biểu thức: 2 2 2 2  x − y 2 1 1   − +  2 1 x y 2xy 3 A = + : ( + ) . − +  ( x ≠ ±y ; 2 2  2 2  x 2xy y
xy x y  x y (x y)(x y) x 2x 2 + + − − + − +  ; x y ≠ 0 )
3) Rút gọn biểu thức A. 2 2  −  Có: x y 2 1 1 2 1 + : ( +  ) .
(Với x ≠ ±y ; 2 2
 x + 2xy + y
xy x y  x − y ; x y ≠ 0 )
(x − y)(x + y) 2 x + y 2  1 = +  : ( ) . 2  (x + y) xy xy  x − y 2 2 1)  x − y 2xy  1 x − y + 2 = + . xy =   (2,0 2 2
 x + y (x + y)  x − y (x − y)(x + y) điểm) 2 2 2 2
x − y + 2xy  x − y + 2xy 3  A = − + 2  2 2 (x y)(x y) (x y)(x y) x 2x 2 − + − + − +  2 2 2 2
x − y + 2xy
x − y + 2xy 3 A = − − 2 2 2
(x − y)(x + y)
(x − y)(x + y) x − 2x + 2 3 A − = 2 x − 2x + 2 Vậy 3 A − =
với x ≠ ±y ; x, y ≠ 0 2 x − 2x + 2
2) Với giá trị nào của x, y thì biểu thức A đạt giá trị nhỏ nhất?
Tìm giá trị nhỏ nhất đó. Có 3 A − = 2 (x −1) +1
Để A đạt giá trị nhỏ nhất thì 3
đạt giá trị lớn nhất 2 (x −1) +1 2) 3 (2,0 +)
đạt giá trị lớn nhất khi chỉ chỉ khi 2 (x −1) +1 đạt 2 (x −1) +1 điểm) giá trị nhỏ nhất Mà 2
(x −1) +1≥1. Dấu “=” xảy ra khi và chỉ khi x = 1 (thỏa mãn điều kiện)
Vậy giá trị nhỏ nhất của A bằng 3 − = 3 − khi và chỉ khi x = 1; 1 y ≠ 0 ; y ≠ 1 ± Bài 2 (4,0 điểm) 1) 1) Phân tích đa thức
(2,0 P = bc(a + d)(b − c) − ac(b + d)(a − c) + ab(c + d)(a − b) Điểm
điểm) thành nhân tử.
Có (b - c) + (a - b) = a – c. Do đó:
P = bc(a + d)(b − c) − ac(b + d) (b − c) + (a − b) + ab(c + d)(a − b)  0,5
P = bc(a + d)(b − c) − ac(b + d)(b − c)
−ac(b + d)(a − b) + ab(c + d)(a − b) 0,5
P = (b − c)[bc(a + d) − ac(b + d)]+ (a − b)[ab(c + d) − ac(b
P = c(b − c)(ab + bd − ab − ad) + a(a − b)(bc + bd − bc − cd 0,5
P =cd(b−c)(b−a)+ad(a−b)(b−c)
P = d(b − c)(a − b)(a − c) 0,5
Vậy P = d (b − c)(a − b)(a − c)
2) Cho các số nguyên a, , b c thoả mãn 3 3 3
(a − b) + (b − c) + (c − a) = 210 . Tính giá trị của biểu thức
A = a − b + b − c + c − a .
Đặt a − b = ;
x b − c = y ; c − a = z 0,5
⇒ x + y + z = 0 và 3 3 3
x + y + z = 210 2)
+) x + y + z = 0 3 3
⇒ z = −(x + y) ⇒ z = −(x + y) (2,0 3 3 3
+)x + y + z = 210 điểm) 3 3 3
hayx + y − (x + y) = 210 0,5 ⇔ 3
− xy(x + y) = 210
⇔ xyz = 70 (vì z = −(x + y) )
Do x, y, z là số nguyên có tổng bằng 0 và xyz = 70 = ( 2) − .( 5 − ).7 nên
x, y, z ∈{ 2 − ; 5; − } 7 0,5
Vậy A = a − b + b − c + c − a =14. 0,5 Bài 3 (3,0 điểm)
1) Tìm số tự nhiên n để B = n3 – n2 – 7n + 10 là số nguyên tố.
Ta có: B = (n – 2)(n2 + n – 5)
B là số nguyên tố nên (n – 2) và (n2 + n – 5) là ước của 1 1)
(1,5 + Nếu n – 2 = 1 thì n = 3 khi đó B = 7 (chọn)
điểm) + Nếu n – 2 = -1 thì n = 1 khi đó B = 3 (chọn)
+ Nếu n2 + n – 5 = 1 thì (n + 3)(n – 2) = 0
Với n là số tự nhiên nên n = 2 khi đó B = 0 (loại)  1 − + 7 n =
+ Nếu n2 + n – 5 = -1 thì n2 + n – 4 = 0 2 ⇔  (loại)  1 − − 7 n =  2
Vậy n = 3; n = 1 thì B là số nguyên tố.
2) Giải phương trình: (x – 3)3 + (2x – 1)3 = (3x – 4)3
Đặt x – 3 = a; 2x – 1 = b thì 3x – 4 = a + b.
Phương trình đã cho trở thành: 3 3 3
a + b = (a + b) 0,5 a = 0 3ab(a b) 0  ⇒ + = ⇒ b = 0  0,5 a + b =  0 2)
(1,5 Trở lại phép đặt, ta có: điểm)  x = 3 x − 3 = 0   1 2x 1 0  − = ⇒ x =   2  0,5 3x − 4 = 0  4 x =  3  1 4
Vậy tập nghiệm của phương trình là S = 3  ; ; 2 3   Bài 4 (7,0 điểm)
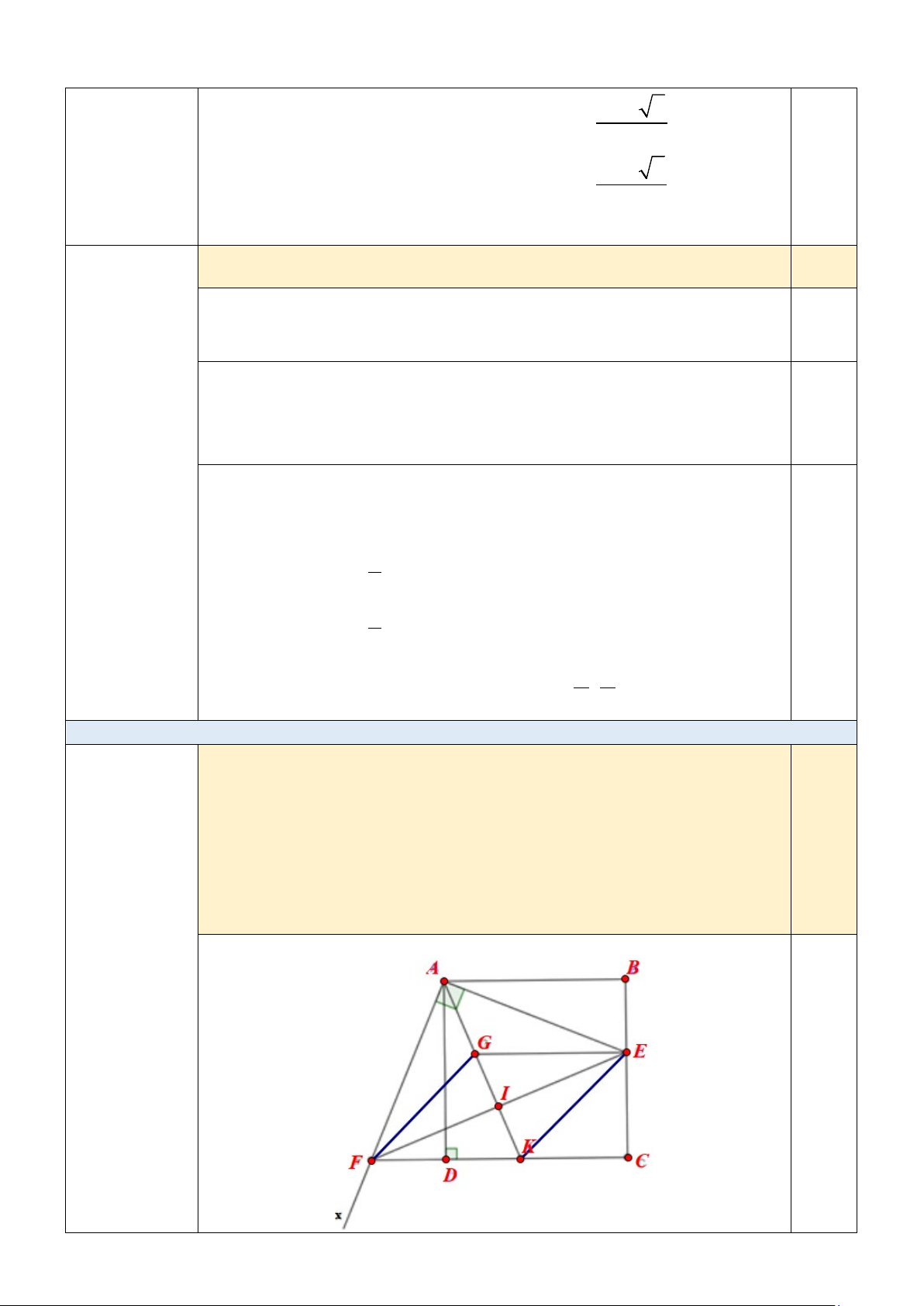
Cho hình vuông ABCD . Gọi E là một điểm trên cạnh BC . Qua A kẻ
tia Ax vuông góc với AE và cắt CD tại F . Trung tuyến AI của tam
giác AEF cắt CD ở K . Đường thẳng qua E song song với AB cắt AI
ở G . Chứng minh rằng:
a) AE = AF và tứ giác EGFK là hình thoi. Điểm b) 2
AF = FK.FC
c) Cho hình vuông ABCD cố định có độ dài cạnh bằng a , chứng minh
rằng khi E di động trên cạnh BC thì chu vi E ∆ KC không đổi Hình vẽ, gt, kl 1) (5,0 điểm) a)
AE = AF và tứ giác EGFK là hình thoi. (2,0
điểm) Chứng minh được B∆AE =∆ AF D (g.c.g) ⇒ AE = AF 0,75 ⇒ A ∆ EF cân tại A
mà AI là trung tuyến (gt)
⇒ AI là trung trực 0,5
⇒ AK là trung trực của đoạn thẳng EF
mà G ∈ AK ⇒ KE = KF,GE = GF (1)
Chứng minh được: E ∆ GI = F ∆ KI(g. . c g) hoặc E ∆ GI = E ∆ KI(g. . c g)
⇒ KF = GE hoặc EK = EG (2) 0,5
Từ (1) và (2) suy ra: EK = EG = GF = FK
⇒ EGFK là hình thoi. 0,25 b) Chứng minh: 2
AF = FK.FC (2,0
điểm) Chứng minh F∆IK đồng dạng với F∆CE FI FK ⇒ =
⇒ FI.FE = FK.FC (3) 1,0 FC FE
Xét tam giác vuông AEF có đường cao AI nên: 2
AF = FI.FE (4) 1,0 Từ (3) và (4) 2
⇒ AF = FK.FC c)
(1,0 Chứng minh rằng: Khi E di động trên BC thì chu vi E ∆ KC không đổi. điểm) Ta có: C
= CE + CK + EK mà FK = KE (cmt) ECK Do đó: C
= CE + CK + KF ECK 0.5
= CE + CK + DK + DF
lại có BE = DF ( B ∆ AE = ∆ AF D ) nên C
= (CK + DK) + (CE + BE) ECK = CD + BC 0,5
= a + a = 2a không đổi Vậy chu vi E
∆ KC không đổi và = 2a khi E di động trên cạnh BC . 2)
2) Cho tam giác MNP có MN = 5cm, MP = 6cm, NP = 7cm. Gọi I là (2,0
giao điểm của ba đường phân giác, G là trọng tâm của tam giác MNP.
điểm) Chứng minh rằng: IG//MP Hình vẽ, gt, kl M D K I G N P
Gọi ND là phân giác của tam giác MNP MD MN 5 MD 5 5 ⇒ = = ⇒ = ⇒ MD = MP = 2,5 (cm) DP NP 7 MP 12 12
Vì MI là phân giác của tam giác MND 0,75 IN MN 5 ⇒ = = = 2 (1) ID MD 2,5
Gọi K là trung điểm của MP.
mà G là trọng tâm của ∆ MNP (gt) nên GN = 2 (2) GK 0,75 Tù (1) và (2) GN IN ⇒ = GK ID
Xét tam giác DNK có GN IN =
⇒ IG / /DK (định lý Thales đảo) GK ID 0,5
hay IG// MP (điều phải chứng minh) Bài 5 (2,0 điểm)
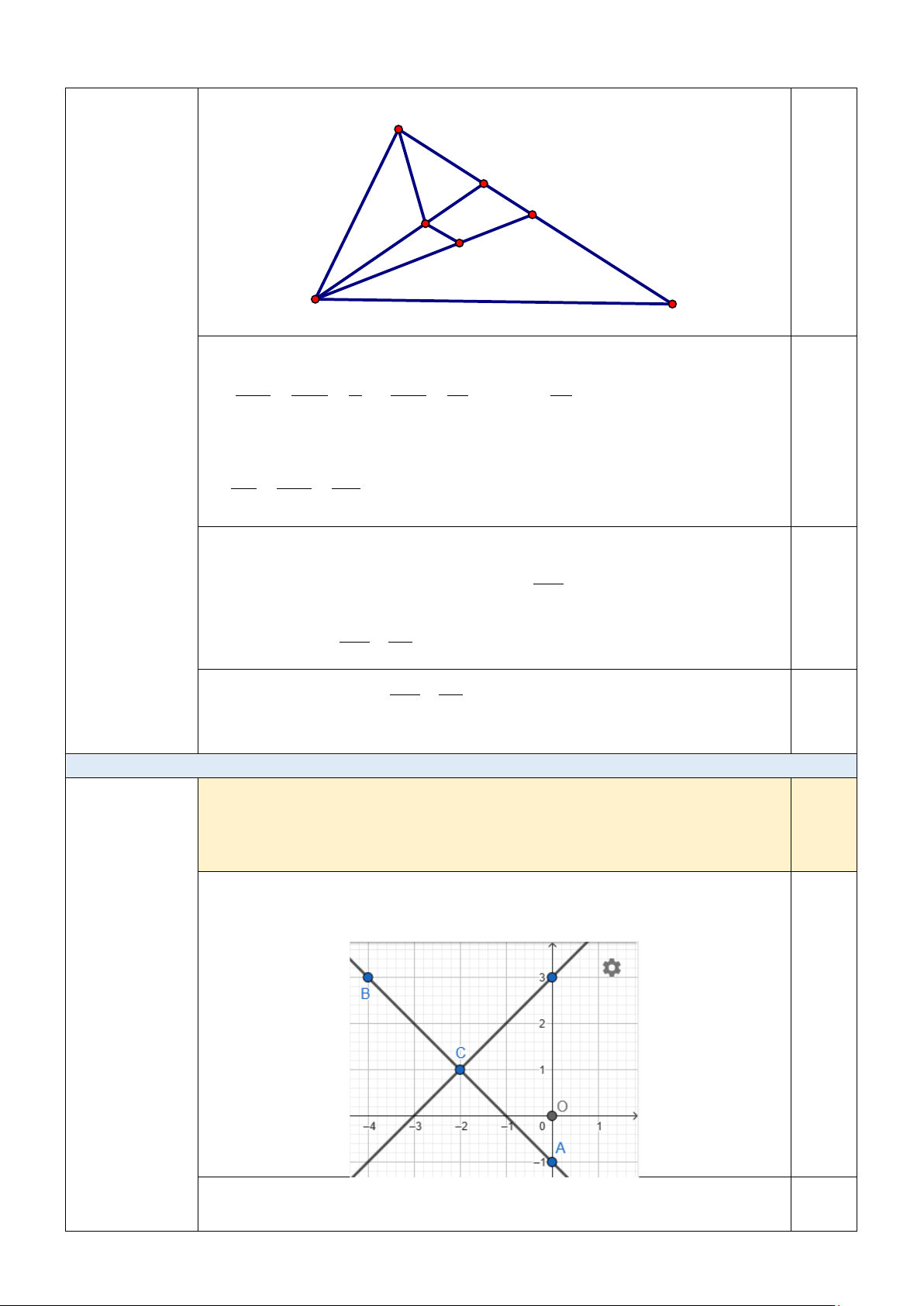
1) Tìm hàm số có đồ thị là đường thẳng (d) thỏa mãn (d) đường trung
trực của AB và A(0; -1); B(-4; 3)
Gọi đường thẳng AB có công thức hàm số là y = ax + b (a khác 0)
+) Vì AB đi qua điểm A(0; -1) nên b = -1
Khi đó đường thẳng AB là y = ax -1 (a khác 0) 1) (1,0 điểm)
+) Vì AB đi qua điểm B(-4; 3) nên a = -1 (thỏa mãn điều kiện)
Do đó đường thẳng AB là y = -x - 1
Vì đường thẳng (d): y = mx + n (m khác 0) vuông góc với AB nên: m.
(-1) = -1 suy ra m = 1 (thỏa mãn). Khi đó (d): y = x + n
Vì C là trung điểm của AB nên C(-2; 1)
Mặt khác (d) đi qua C(-2; 1) nên -2 + n = 1 ⇒ n = 3
Vậy hàm số cần tìm là y = x + 3
2) Chứng minh rằng: Nếu xyz = 1 thì 1 1 1 + + =1
1+ x + xy 1+ y + yz 1+ z + zx 1 1 1 Có S = + +
1+ x + xy 1+ y + yz 1+ z + zx z xz 1 2) S = + + 2 (1,0
z + zx + xyz xz + xyz + xyz 1+ z + zx điểm) z xz 1 S = + + (vì xyz = 1)
z + zx +1 xz +1+ z 1+ z + zx z + xz +1 S =
=1 (điều phải chứng minh) z + zx +1 • Chú ý:
- HS vẽ hình quá sai, không chấm.
- Mọi cách làm khác của học sinh, nếu đúng vẫn cho điểm tối đa.
--------------------Hết-------------------
Document Outline

• a) và tứ giác là hình thoi.
• b)
• c) Cho hình vuông cố định có độ dài cạnh bằng , chứng minh rằng khi di động trên cạnh thì chu vi không đổi.
• 2) Cho tam giác MNP có MN = 5cm, MP = 6cm, NP = 7cm. Gọi I là giao điểm của ba đường phân giác, G là trọng tâm của tam giác MNP. Chứng minh rằng: IG//MP