Đề khảo sát năng lực Toán 6 năm 2022 – 2023 phòng GD&ĐT Ninh Giang – Hải Dương
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 6 đề khảo sát năng lực học sinh môn Toán 6 năm học 2022 – 2023 phòng Giáo dục và Đào tạo huyện Ninh Giang, tỉnh Hải Dương; đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm; kỳ thi được diễn ra vào ngày 13 tháng 01 năm 2023.
Preview text:
UBND HUYỆN NINH GIANG
ĐỀ KHẢO SÁT NĂNG LỰC HỌC SINH
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học 2022-2023 Môn: TOÁN 6
Ngày khảo sát: 13/1/2023
Thời gian làm bài: 150 phút
(Đề gồm 01 trang 5 câu)
Câu 1. ( 3 điểm) a) Tính ( 4 2 ) ( 3 3 4 .24.16 : 4 .8 )
b) Cho tập hợp S = {1;4;7;10;13;16; }
... . Hỏi số 2023 có là phần tử của S hay không?
c) Chứng minh rằng: (ab − ba)9 ( a > b) Câu 2. (2 điểm) a) Tìm x biết: x 1+ x+2 x 3 + 3 − 2.3 = 270
b) Tìm số học sinh của trường THCS. Biết rằng số học sinh của trường đó nếu xếp
thành 17 hàng thì dư 8 em, xếp thành 25 hàng thì dư 16 em và số học sinh nhỏ hơn 800. Câu 3. (2 điểm) a) Cho 2 3 100
B = 3 + 3 + 3 + ... + 3 . Chứng minh rằng 2B + 3 không là số chính phương
b) Tìm các số nguyên x, y biết: 2 25 − y = 8(x − 2023)2
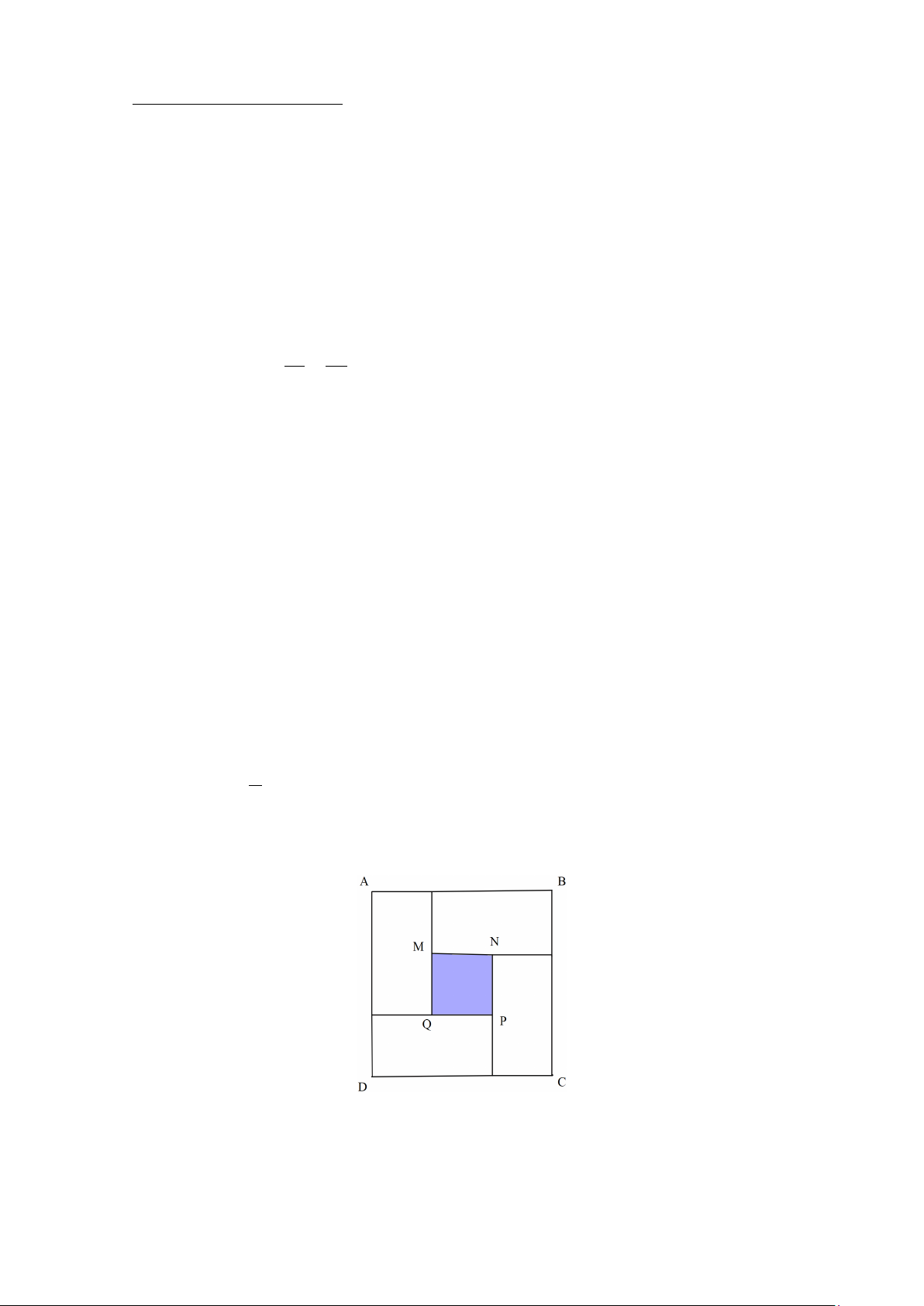
Câu 4. (2 điểm) Người ta xếp bốn hình chữ nhật bằng nhau để được một hình vuông
ABCD có diện tích 625cm2 và bên trong là một hình vuông MNPQ . Biết hình chữ nhật
có chiều dài bằng 3 chiều rộng (như hình vẽ). 2
a) Tính chu vi hình vuông ABCD
b) Tính diện tích hình vuông MNPQ .
Câu 5. (1 điểm) Tìm các số nguyên tố p,q và số nguyên x thỏa mãn 5 x + px + 3q = 0
------------------ Hết ------------------ HƯỚNG DẪN CHẤM Câu Đáp án Điểm Câu 1 a) Tính ( 4 2 ) ( 3 3 4 .24.16 : 4 .8 ) ( 0,5 4 2 ) ( 3 3 ) = ( 8 3 8 ) ( 6 9 4 .24.16 : 4 .8 2 .3.2 .2 : 2 .2 ) = ( 19 ) ( 15 3.2 : 2 ) 0,25 4 = 3.2 = 48 0,25
b) Tập hợp S gồm các số tự nhiên chia 3 dư 1 0,25
Chứng minh được 2023 chia 3 dư 1 0,5
Vậy 2023 là phần tử của S 0,25
c) Chứng minh rằng: (ab − ba)9 ( a > b) 0,5
ab − ba =10a + b − (10b + a) = 9a − 9b 9 0,5
Câu 2 a) Tìm x biết: x 1+ x+2 x 3 + 3 − 2.3 = 270 x 1 + x+2 x 3 + 3 − 2.3 = 270 0,5 x x x ⇒ 3.3 + 9.3 − 2.3 = 270 x ⇒10.3 = 270 0,25 x ⇒ 3 = 27 ⇒ x = 3 0,25
b) Gọi số học sinh trường A là x ( * x ∈ N ,x < 800)
Theo bài ra: x chia hết cho 8
x chia 17 dư 8 => x + 9 chia hết cho 17 0,25
x chia 25 dư 16 => x+9 chia hết cho 25 => x + 9 thuộc BC(17,25)
Tính được BCNN(17, 25)=425 0,25
=> x + 9∈B(425) = (0; 425; 850,..) ⇒ x ∈(416; 841; ..) 0,25 Mà x nhỏ hơn 800 0,25 => x = 416 Câu 3 a) 2 3 4 100 B = 3 + 3 + 3 + 3 + ... + 3 0,25 2 3 4 101 ⇒ 3B = 3 + 3 + 3 + ... + 3 − = ( 2 3 4 101 + + + + ) −( 2 3 4 100 3B B 3 3 3 ... 3
3 + 3 + 3 + 3 + ... + 3 ) 0,25 101 101 2B = 3 − 3 ⇒ 2B + 3 = 3 0,25 Vì 101
3 là số nguyên tố với số mũ lẻ nên 2B + 3 không là số 0,25 chính phương.
b) Tìm các số nguyên x, y biết: 2 25 − y = 8(x − 2023)2 0,25 Có ( − )2 8 x 2023 ≥ 0 với mọi x 2 ⇒ 25 − y ≥ 0 Theo đề bài => 2 2
25 − y 8 ⇒ 25 − y ∈{24;16;8; } 0 0,25 TH1: 2 25 − y = 24 ⇒ y = 1 ± => ( − )2 = ⇒ ( − )2 8 x 2023 24 x 2023 = 3(loại) TH2: 2 25 − y =16 ⇒ y = 3 ± ⇒ ( − )2 = ⇒ ( − )2 8 x 2023 16 x 2023 = 2(loại) 0,5 TH3: 2 2
25 − y = 8 ⇒ y =17 (loại) TH4: 2 25 − y = 0 ⇒ y = 5 ± ⇒ ( − )2 = ⇒ ( − )2 8 x 2023 0 x 2023 = 0 ⇒ x = 2023 Vậy (x,y)∈ ( { 2023;5);(2023;− 5)} Câu 4
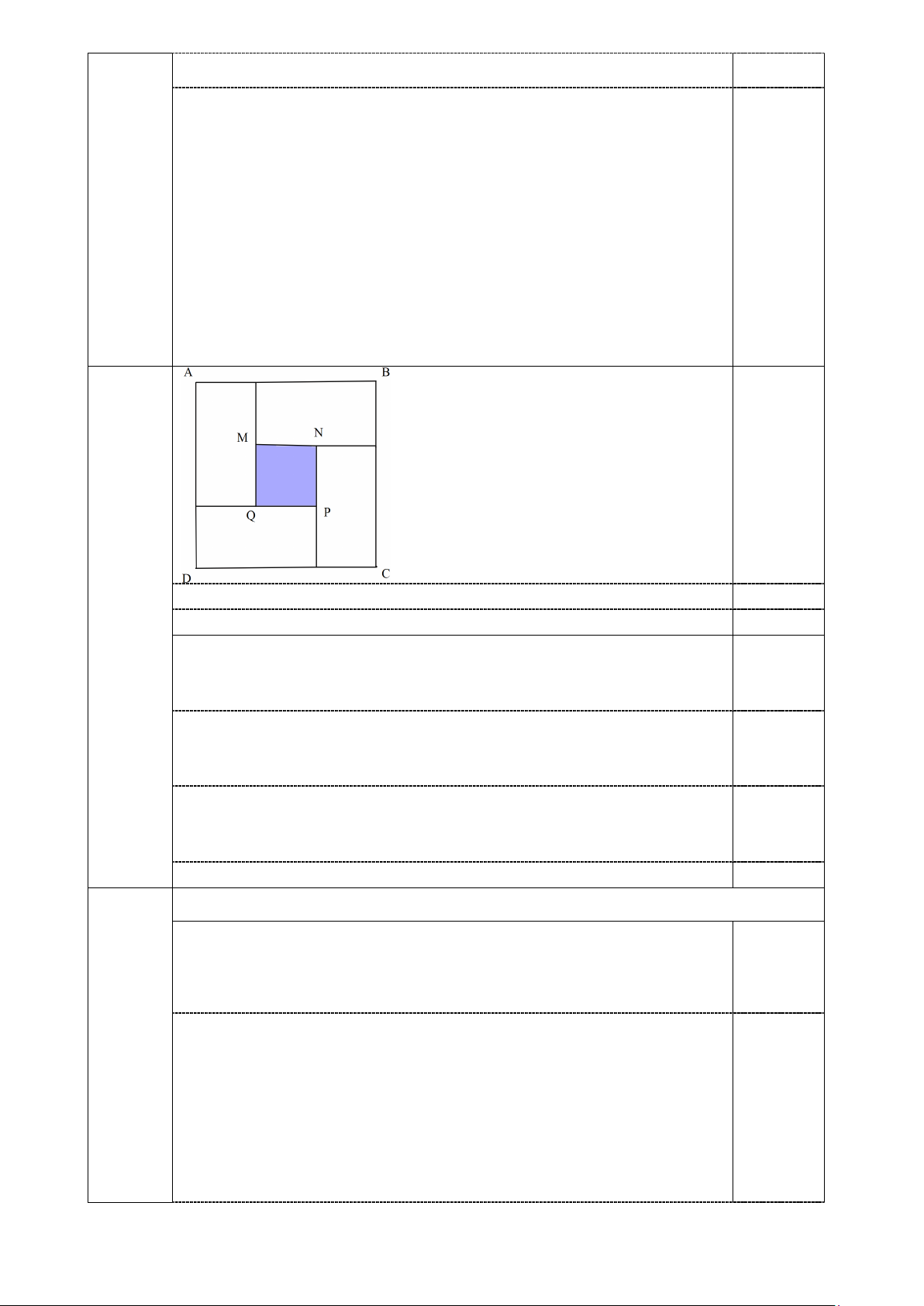
a) Độ dài cạnh của hình vuông ABCD là 25cm 0,5
=> Chu vi hình vuông ABCD là 25.4=100cm 0,5
b) Vì tỉ lệ chiều dài và chiều rộng của hình chữ nhật là 3/2
=>Gọi chiều dài mỗi hình chữ nhật là 3x (cm) 0,25
=> chiều rộng là 2x (cm)
Theo hình vẽ ta có: chiều dài + chiều rộng = AB = 25 cm
=> 3x + 2x = 25 => x = 5 0,25
=> chiều dài = 15cm; chiều rộng = 10cm
Diện tích một hình chữ nhật là 15.10=150 cm2
=> diện tích của 4 hình chữ nhật xung quanh là: 0,25 150.4=600cm2
Diện tích hình vuông MNPQ là: 625 – 600 = 25cm2 0,25
Câu 5 Tìm các số nguyên tố p,q và số nguyên x thỏa mãn 5 x + px + 3q = 0 Ta có 5 4
x + px + 3q = 0 ⇔ x(x + p) = 3q − .
Vì q là số nguyên tố và x là số nguyên nên từ phương trình 0,25 trên ta suy ra x ∈{ −1; 3 − ;−q; 3q} − .
Ta xét các trường hợp sau: + Nếu x = 1
− , khi đó từ phương trình trên ta được 1+ p = 3q .
Do q là số nguyên tố nên: 0,25
- Khi q = 2 thì ta được p = 5.
- Khi q > 2 thì 3q là số lẻ nên p là số nguyên tố chẵn. Do
đó p = 2 nên q =1 không phải là số nguyên tố. + Nếu x = 3
− , khi đó từ phương trình trên ta được p + 81= q .
Do đó p là số nguyên tố chẵn và q là số nguyên tố lẻ. Từ đó 0,25 ta được p = 2;q = 83.
+ Nếu x = −qkhi đó từ phương trình trên ta được 4 p + p =3.
Trường hợp này không xảy ra do p và q là số nguyên tố nên 4 p + p > 3. 0,25 + Nếu x = 3q
− , khi đó phương trình trên ta được 4 p + 81p =1.
Trường hợp này không xảy ra do p và q là số nguyên tố nên 4 p + 81p >1.
Vậy các bộ số (x;p;q) thỏa mãn yêu cầu bài toán là ( 1 − ;5;2),( 3 − ;2;83).