Đề kiểm tra 1 tiết Giải tích 12 chương 1 (Hàm số) trường THPT Ba Tơ – Quảng Ngãi

Đề kiểm tra 1 tiết Giải tích 12 chương 1 – ứng dụng đạo hàm để khảo sát sự biến thiên và vẽ đồ thị hàm số trường THPT Ba Tơ – Quảng Ngãi gồm 10 mã đề, mỗi đề gồm 25 câu hỏi trắc nghiệm.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

30 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1. Đồ thị trong hình dưới là của hàm số nào.
x
2
-2
y
1
O
-1
A.
42
2yx x=- + B.
3
3yx x=- + . C.
3
3yx x=-. D.
42
2yx x=- .
Câu 2. Cho hàm số
32
1
231
3
yxxx=-++
có đồ thị là
()
C . Tiếp tuyến của
()
C song song với đường
thẳng
:31yxD=+ có phương trình là:
A.
31yx=-. B.
26
3
3
yx=-
. C. 32yx=-. D.
29
3
3
yx=-
.
Câu 3. Hàm số
32
394yx x x=- + + + đồng biến trên khoảng:
A.
()
3;+¥ . B.
()
3;1- . C.
()
;3-¥ - . D.
()
1; 3- .
Câu 4. Cho hàm số
()
yfx= xác định, liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là đúng ?
A. Hàm số có giá trị cực đại bằng
3 . B. Hàm số có GTLN bằng 1, GTNN bằng
1
3
-
.
C. Hàm số có hai điểm cực trị. D. Đồ thị hàm số không cắt trục hoành.
Câu 5. Giá trị nhỏ nhất của hàm số
1
5
yx
x
=-+ trên đoạn
1
;5
2
éù
êú
êú
ëû
bằng:
A.
5
2
-
. B.
1
5
. C. 3- . D. 5- .
Câu 6. Hàm số
42
31yxx=- - + có:
A. Một cực đại và hai cực tiểu. B. Một cực tiểu và hai cực đại.
C. Một cực đại duy nhất. D. Một cực tiểu duy nhất.
0
y
x
'y
-¥
+¥
1
1
3
-
-¥
1
+¥
-
-
3
0 +
Câu 7. Giá trị của m để đường thẳng :3 0dx y m++= cắt đồ thị hàm số
23
1
x
y
x
-
=
-
tại hai điểm
M
,
N sao cho tam giác AMN vuông tại điểm
()
1; 0A là:
A.
6m =
. B.
4m =
. C.
6m =-
. D.
4m =-
.
Câu 8. Với tất cả giá trị nào của
m thì hàm số
()
4
112ymx m x m
2
=+-+- chỉ có một cực trị:
A.
1m ³
. B.
0m £
. C.
01m££
. D.
0
1
m
m
é
£
ê
ê
³
ë
.
Câu 9: Hàm số nào sau đây là hàm số nghịch biến trên
?
A.
32
32yx x
B.
32
22yxxx
C.
42
22yx x
D.
3
1
x
y
x
Câu 10. Khẳng định nào sau đây là đúng về tính đơn điệu của hàm số
32
31yx x ?
A. Hàm số nghịch biến trên khoảng

0; 2 B. Hàm số đồng biến trên khoảng

0; 2
C. Hàm số nghịch biến trên khoảng

0;  D. Hàm số đồng biến trên khoảng

;2 .
Câu 11. Hàm số
42
21yx x đồng biến trên khoảng nào ?
A. (;0) B. (0; ) C. (1; ) D. (1;0)
Câu 12.
Tìm giá trị của m để hàm số
32
3212yx mx m x đạt cực trị tại 1
x
A. 1m B. 1m  C. 2m D. Không tồn tại m
Câu 13. Có bao nhiêu giá trị của m để đồ thị hàm số
42
2( 1)yx m x m có 3 điểm cực trị
,,
A
BC
sao cho 2BC , trong đó
A
là điểm cực trị thuộc trục tung,
B
và C là 2 điểm cực trị còn
lại
A. 0 B. 2 C. 1 D. 3
Câu 14. Đồ thị hàm số
12
2
y
x
có đường tiệm cận đứng và đường tiệm cận ngang là ?
A. 2, 2xy B.
1
2,
2
xy
C. 2, 2xy D.
1
,2.
2
xy
Câu 15.
Đồ thị hàm số
2
1yxx x có bao nhiêu đường tiệm cận ngang ?
A. 0 B. 1 C. 2 D. 3
Câu 16.
Cho đồ thị hàm số ( C)
3
33yx x. Khẳng định nào sau đây là sai ?
A. Đồ thị (C) nhận điểm (0;3)I làm tâm đối xứng.
B. Đồ thị (C) cắt trục hoành tại hai điểm phân biệt.
C. Đồ thị (C) tiếp xúc với đường thẳng
5
y
D. Đồ thị (C) cắt trục tung tại một điểm.
Câu 17. Cho đồ thị hàm số ( C)
42
23yx x . Khẳng định nào sau đây là sai ?
A. Đồ thị (C) nhận trục tung làm trục đối xứng
B. Đồ thị (C) cắt trục hoành tại hai điểm phân biệt.
C. Đồ thị (C) có 3 điểm cực trị tạo thành một tam giác vuông.
D. Đồ thị (C) tiếp xúc với đường thẳng 2
y

Câu 18. Bảng biến thiên sau của hàm số nào ?
x -
0 2

y
' - 0 + 0 -
y
+ 0
-4 -
A.
32
3yx x B.
32
3yx x C.
32
34yx x D.
32
34yx x
Câu 19. Gọi , AB là giao điểm của hai đồ thị

21
:
1
x
Cy
x
và đường thẳng :2dy x . Khi đó độ
dài đoạn
A
B là:
A.
4
A
B
B.
22AB
C.
10AB
D.
23AB
.
Câu 20
.Số giao điểm của đồ thị hàm số
2
(3)( 4)yx xx với trục hoành là :
A. 2 B. 3 C. 0 D. 1
Câu 21.
Tiếp tuyến của đồ thị hàm số
2
1
x
y
x
tại giao điểm với trục Ox có phương trình :
A. 2yx B. 2yx C. 2yx D. 2yx
Câu 22.
Cho hàm số
32
y
ax bx cx d
0a có đồ thị như hình vẽ dưới đây. Khẳng định nào
sau đây về dấu của
, , , abcd là đúng nhất ?
A. , 0.ad B. 0, 0 .ac b C. , , , 0.abcd D. , 0, 0.ad c
Câu 23.
Đồ thị hàm số
2
31
76
x
y
xx

có số đường tiệm cận là ?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 24. Kí hiệu m và
M
lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số
2
4
1
xx
y
x

trên
đoạn
0;3


. Tính giá trị của tỉ số .
M
m
A.
5
.
3
B.
4
.
3
C. 2. D.
2
.
3
Câu 25.
Với các giá trị nào của tham số m thì hàm số
()
122mxm
y
xm
+++
=
+
nghịch biến trên khoảng
()
1;-+¥?
A
. 1m < . B. 2m > . C.
1
2
m
m
é
<
ê
ê
>
ë
. D.
12m£<
.
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1. Đồ thị ở hình bên là đồ thị của hàm số nào
trong bốn hàm số dưới đây ?
A.
2
1
x
y
x
+
=
-
. B.
2
1
x
y
x
-
=
+
.
C.
2
1
x
y
x
-
=
+
. D.
2
1
x
y
x
-
=
-
.
x
-
1
y
1
O
Câu 2. Hệ số góc của tiếp tuyến đồ thị hàm số
1
1
x
y
x
-
=
+
tại giao điểm của đồ thị hàm số với trục tung
bằng:
A. 2. B. 1. C. - 2 . D. 1- .
Câu 3. Cho hàm số
()
yfx=
có đồ thị như hình vẽ bên.
Khẳng định nào sau đây là
sai:
A. Hàm số đồng biến trên khoảng
()
;3-¥
và
()
1; +¥
.
B. Hàm số đạt cực trị tại các điểm 0x = và 1x = .
C. Hàm số đồng biến trên khoảng
()
;0-¥ và
()
1; +¥ .
D. Hàm số nghịch biến trên khoảng
()
0;1 .
x
3
2
y
1
O
-1
Câu 4. Cho hàm số
()
yfx= liên tục trên và có bảng biến thiên như hình dưới đây. Số mệnh đề sai
trong các mệnh đề sau đây?
I.
Hàm số đồng biến trên các khoảng
()
;5-¥ - và
()
3; 2-- .
II. Hàm số đồng biến trên khoảng
()
;5-¥ .
III. Hàm số nghịch biến trên khoảng
()
2;-+¥.
IV. Hàm số đồng biến trên khoảng
()
;2-¥ - .
A. 1. B. 2 . C. 3 . D. 4 .
Câu 5. Hàm số
1
21
x
y
x
-
=
+
đạt giá trị lớn nhất trên đoạn
[
]
0;2 tại:
x
'y
y
-
¥
3-
2
-
+
¥
0 0
-
+
+
-
¥
5
0
-
¥
A.
0x =
. B.
2x =
. C.
3x =
. D.
1
2
x
=- .
Câu 6. Đồ thị hàm số nào sau đây không có cực trị ?
A
.
32
yx x x=--. B.
32
1yxx=- + + . C.
32
yxxx=- + - . D.
32
1yx x=+-.
Câu 7. Tìm
m
để đường thẳng
:dy x m=-
cắt đồ thị hàm số
()
1
:
1
x
Cy
x
+
=
-
tại hai điểm phân biệt
, AB
sao cho 32AB = .
A. 2m = . B. 4m = . C. 1m = . D. 3m = .
Câu 8.
Số đường tiệm cận của đồ thị hàm số
2
2
4
34
x
y
xx
-
=
--
là:
A
.
0
. B.
2
. C.
3
. D.
1
.
Câu 9.
Cho hàm số
()yfx
liên tục trên và phương trình
() 0fx
có ba nghiệm thực
phân biệt. Xét các hình dưới đây, những hình nào có thể là đồ thị của hàm số
()
f
x ?
(1) (2)
(3) (4)
A. 1 và 2. B. 1, 2 và 4. C. 1 và 3. D. 2 và 4.
Câu 10. Tìm tổng giá trị lớn nhất và nhỏ nhất của hàm số
42
f(x) 2x 4x 10
trên đoạn [0;2] ?
A. 12; 6 B. 12 C. 6 D. 6
Câu 11. Tìm giá trị lớn nhất của hàm số

2
42
3
xx
fx
x

trên đoạn
1; 3 .
A.

1;3
max 2.fx
B.


1;3
14
max .
5
fx
C.


1;3
5
max .
2
fx
D.


1;3
26
max .
3
fx
Câu 12.
Tìm m sao cho hàm số
32
312yfx x mx m x đạt cực đại tại 2.x
A. 1.m B. 3.m C. 1.m  D. .m 
Câu 13: Cho đồ thị hàm số (C):
2
x1
y
xx2

, trong các kết luận sau, kết luận nào đúng:
A. Đồ thị hàm số (C) có một tiệm cận đứng là x2 và một tiệm cận ngang là trục hoành.
B. Đồ thị hàm số (C) có hai tiệm cận đứng là x2 và x1 một tiệm cận ngang là trục hoành.
C. Đồ thị hàm số (C) có một tiệm cận ngang là trục tung và hai tiệm cận đứng là x2và x1.
D. Đồ thị hàm số (C) có một tiệm cận ngang là trục tung và một tiệm cận đứng duy nhất là x=1.
Câu 14: Với giá trị nào của m thì hàm số
mx 1
y
x1
tăng trên từng khoảng xác định ?
A. m0 B. m1 C. m1 D. m0
Câu 15: Gọi M và m lần lượt là GTLN và GTNN của hàm số
2
yx1x trên tập xác định. Khi đó
M – m bằng:
A. 1 B. 2 C. 3 D. đáp số khác
Câu 16.Đồthịởhình bên làđồthịcủahàmsố
nàotrongbốnhàmsốdướiđây?
A. 
4
2yx 
B.

32
32yx x .
C.
=- +
42
22yx x
.
D.

42
22yx x .
x
y
O
Câu17.
Cho hàm số
+
=
-
21
2
x
y
x
có đồ thị là
()
C . Phương trình tiếp tuyến của
()
C có hệ số góc bằng
5 là:
A.
=- +52yx
và
=- +522yx
. B.
=+52yx
và
=- +522yx
.
C.
=- +52yx
và
=- -522yx
. D.
=- -52yx
và
=- +522yx
.
Câu18.Hàmsố
42
2yxx=- - - nghịchbiếntrênkhoảng:
A.
()
0;+¥
. B.
()
;0-¥
. C.
()
1;-+¥
. D.
()
;1-¥
.
Câu19.Giátrịlớnnhấtcủahàmsố
54yx=-trênđoạn
[
]
1;1-
bằng:
A.9. B.3. C.1. D.0.
Câu20.Tìmtấtcảgiátrịcủa
m
đểphươngtrình
3
0
2
x
m
x
+
-=
-
cónghiệmâm:
A.
3
2
m
³- . B.
3
1
2
m
-< <. C.
3
1
2
m
-£ £.D.
3
2
m
>- .
Câu21.
Tìm
m
để hàm số
32
31yx xm=- + + - có giá trị cực đại là
max
y , giá trị cực tiểu là
min
y thỏa
mãn
max min
.5yy= :
A. 4m =- hoặc 2m =- . B. 4m = hoặc 2m = .
C.
4m =- hoặc 2m = . D. 4m = hoặc 2m =- .
Câu 22.
Cho hàm số ( )yfx có bảng biến thiên sau:
Khẳng định nào dưới đây là khẳng định sai ?
A. Đồ thị hàm số có một tiệm cận ngang 2.y B. Hàm số đạt cực đại và cực tiểu.
C. min ( )
CT
f
xy và max ( ) .
CÑ
fx y D. Hàm số đồng biến trên khoảng
2; .
Câu 23. Tìm giá trị cực tiểu
CT
y của hàm số
2
21
.
1
xx
y
x

A. 0.
CT
y B. 7.
CT
y  C. 1.
CT
y D. 8.
CT
y 
Câu 24.
Tìm giá trị nhỏ nhất của hàm số
32
291yx x trên đoạn

4; 1.
A.

4; 1
miny 1.

B.

4; 1
miny 8.

C.

4; 1
miny 28.

D.

4; 1
miny 5.

Câu 25.
Đồ thị của hàm số nào dưới đây có tiệm cận đứng ?
A.
2
23.yx x B.
2
2
1
.
1
x
y
xx

C.
2
2
1
.
1
xx
y
x

D.
3
21.yx x
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu1.Đồthịhìnhbênlàđồthịcủahàm
sốnàosauđây?
A.
32
31yx x=- +.
B.
42
22yx x=- + -
.
C.
42
21yx x=- + + .
D.
42
21yx x=- +.
x
y
1
-
1
O
2
Câu2.Đồthịhàmsố
2
42
1
32
x
y
xx
+
=
++
cóbaonhiêuđườngtiệmcận?
A.0. B. 1. C.2. D. 3.
Câu3.Hàmsố
21
3
x
y
x
-
=
-
nghịchbiếntrênkhoảngnào?
A.
()
;-¥ +¥
. B.
()
;4-¥
. C.
()
0;+¥
. D.
()
3;4
.
Câu4.Giátrịlớnnhấtcủahàmsố
2
4
2
y
x
=
+
là:
A.3. B. 2. C.
5- . D.10.
Câu5.Tìmtấtcảcácgiátrịcủa
m
đểPT
42
21 0xx m-++=cóbốnnghiệmphânbiệt.
A.
1.m <- . B. 11m-< < . C. 1m > . D. 10m-< <
Câu6.Tìm
m đểhàmsố
()
322
1
42
3
yxmxm x=++-+
đạtcựctiểutại 1.x = 
A.
2m =- . B. 1m =- . C. 1m = . D.Khôngcó m .
Câu7.Đồthị
()
C củahàmsố
2016
21
x
y
x
-
=
+
cắttrụctungtạiđiểm
M
cótọađộ?
A.
()
0;0M
. B.
()
0; 2016M -
. C.
()
2016;0M
. D.
()
2016; 2016-
.
Câu 8.
Cho hàm số
2
ax b
y
x
có đồ thị
.C Đồ thị

C nhận đường thẳng 3y làm tiệm cận
ngang và

C
đi qua điểm

3;1 .A
Tính giá trị của biểu thức .
P
ab
A. 3.P B. 5.P  C. 8.P  D. 5.P
Câu9.
Cho đồ thị của hàm số
42
yax bx c (0)a như hình vẽ. Khẳng định nào sau đây là
khẳng định đúng ?
A. 0, 0, 0.abc B. 0, 0, 0.abc C. 0, 0, 0.abc D. 0, 0, 0.abc
Câu10.Chohàmsố
1
21
x
y
x
+
=
-
.Chọnphươngánđúngtrongcácphươngándướiđây?
A.
[]
1;2
1
min
2
y
-
= . B.
[]
1;0
max 0y
-
=
. C.
[]
3;5
11
min
4
y
= . D.
[]
1;1
1
max
2
y
-
= .
Câu11.Trongcáchàmsốsau,hàmsốnàovừacókhoảngđồngbiếnvừacókhoảngnghịch
biếntrêntậpxácđịnhcủanó.
()
21
. .
1
x
y
x
+
I=
+

()
42
. 2.yxxII = - + -
()
3
. 3 4.yx xIII = + -
A.
()
I . B.
()
II . C.
()( )
;II III . D.
()( )
;I III .
Câu12.Tìmđiểmcựctiểucủađồthịhàmsố
32
34yxx=- + +
.
A.(0;2). B.
()
0;4M
. C.
()
2;0M
. D.(0;4).
Câu13.Chohàmsố
()
31
12
x
yfx
+
==
-
.Khẳngđịnhnàodướiđâylàkhẳngđịnhđúng?
A.Đồthịhàmsố
()
yfx= cótiệmcậnnganglà 3y = .
B.Đồthịhàmsố
()
yfx=
cótiệmcậnđứnglà
1x =
.
C.Đồthịhàmsố
()
yfx= cótiệmcậnnganglà
3
2
y =- .
D.Đồthịhàmsố
()
yfx= khôngcótiệmcận.
Câu14.Đồthịhàmsố
32
32yx x x=- -
cắttrụchoànhtạibaonhiêuđiểm?
A.
4 . B. 3 . C. 2 . D.1.
Câu15.Đườngthẳng
ym= cắtđồthịhàmsố
3
32yx x=-+tạibađiểmphânbiệtkhi:
A.
04m£<. B. 4m > . C. 04m<£. D.04m<<.
Câu16.Chohàmsố
32
31yxx=- + + ,cóđồthịlà
()
C .Viếtphươngtrìnhtiếptuyếncủađồthị
hàmsố
()
C
tạiđiểm
()
3;1A
.
A.
20 9yx=-. B. 9280xy+- =. C. 920yx=+. D.9280xy-+ =.
Câu17.Hàmsố
32
2017
3
m
yxxx=+++
cócựctrịkhivàchỉkhi:
A.
1m £ . B.
1
0
m
m
ì
<
ï
ï
í
ï
¹
ï
î
. C.
1
0
m
m
ì
£
ï
ï
í
ï
¹
ï
î
. D. 1m < .
Câu 18.
Hàm số
42
4
f
xx x có số điểm cực trị là ?
A. 1. B. 3. C. 2. D. 4.
Câu 19.
Tìm giá trị lớn nhất và nhỏ nhất của hàm số
32
3910fx x x x trên
4; 2 .
A.


4;2
4;2
max 37; min 5.fx fx
 B.


4;2
4;2
max 40; min 12.fx fx

C.


4;2
4;2
max 30; min 4.fx fx
 D.


4;2
4;2
max 50; min 6.fx fx

Câu 20. Cho
M
là điểm có tọa độ nguyên, thuộc đồ thị hàm số
2
39
.
2
xx
y
x

Hỏi có bao nhiêu
điểm
M
thỏa mãn bài toán ?
A. 5. B. 4. C. 6. D. 7.
Câu 21.
Cho hàm số
3
:y 3Cxx
và
:12dy mx
. Tìm tất cả giá trị thực của tham số
m
sao cho
d
cắt
C tại ba điểm phân biệt.
A.
9
4
m 
và 0.m B.
9
.
4
m 
C. 0.m D.
9
4
m 
và 3.m 
Câu22.Hàmsốnàosauđâyđồngbiếntrên .
A.
-
=
+
1
2
x
y
x
.B.
=--
32
11
32
yx xx
. C.
=--
4
42yx x
. D.
=+ +-
32
331yx x x
.
Câu23.Hàmsốbậcba
=+++
32
yax bx cxdcóthểcóbaonhiêucựctrị?
A.
1, 2 hoặc
3
. B.
0
hoặc
2
. C. 0, 1 hoặc
2
. D.
2
.
Câu24.Gọi
, ,
A
BClầnlượtlàbađiểmcựctrịcủađồthìhàmsố =-+
42
241yx x .Tínhdiện
tíchcủatamgiác
ABC .
A.
4 . B. 2 . C.1. D. 2 .
Câu 25.Biếtrằngđồthịhàmsố
+
=
-
1
2
ax
y
bx
cótiệmcậnđứnglà = 2x vàtiệmcậnnganglà
= 3y .Tínhgiátrịcủabiểuthức
=+Pab
.
A.
= 1
P
. B.
= 4
P
. C.
= 0P
. D.
= 5P
.
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1. Đường cong trong hình dưới đây là đồ thị của hàm số nào ?
A.
25
.
2
x
y
x
B.
25
.
2
x
y
x
C.
25
.
2
x
y
x
D.
25
.
2
x
y
x
Câu 2.
Đồ thị hàm số
2
2
1
x
y
x
có bao nhiêu đường tiệm cận ?
A. 1. B. 2. C. 3. D. 0.
Câu 3. Tìm điều kiện của , , abc để hàm số
32
yax bx cxd (0)a đồng biến trên
.
A.
2
0, 3 0.abac B.
2
0, 3 0.abac C.
2
0, 3 0.abac D.
2
0, 3 0.abac
Câu 4.
Tìm giá trị cực tiểu
CT
y của hàm số
2
2
21 .
1
x
yx
x

A.
33 1.
CT
y 
B.
1.
CT
y 
C.
33.
CT
y
D.
133.
CT
y 
Câu 5.
Biết đường thẳng
:21dy x
cắt đồ thị

C của hàm số
2
35yxx tại điểm duy nhất,
kí hiệu

00
;
x
y
là tọa độ của điểm đó. Tìm
0
.y
A.
0
2.y B.
0
3.y C.
0
1.y D.
0
4.y
Câu 6.
Tìm giá trị lớn nhất của hàm số

2
23
2
xx
fx
x

trên đoạn
0;3 .
A.


0;3
12
max .
5
fx B.


0;3
max 12.fx C.


0;3
17
max .
5
fx D.


0;3
14
max .
5
fx
Câu 7.
Tìm tất cả các giá trị thực của a sao cho đồ thị hàm số
2
2
1
32
x
y
x
xa a

có đúng một tiệm
cận đứng.
A.
3
.
2
a 
B. 0a hoặc 3.a C. 1a hoặc 2.a D 2.a 
Câu 8. Hãy xácđịnh hệ số , , abcđểhàm số
42
yaxbxc=++cóđồthịnhưhìnhvẽ.
A.
4, 2, 2abc=- =- = .
B.
1
,2,2
4
ab c==-=
.
C. 4, 2, 2abc===-.
D.
1
,2,2
4
abc===
.
x
-
2
-3
y
2
O
4
3
2
-2
Câu9.
Cho hàm số
()
yfx=
có bảng biến thiên như hình vẽ. Mệnh đề nào đúng trong các mệnh đề
dưới đây.
A.Hàmsốđồngbiếntrêncáckhoảng
1
;
2
æö
÷
ç
-¥ -
÷
ç
÷
ç
èø
và
()
3;+¥ .
B.Hàmsốđồngbiếntrênkhoảng
1
;
2
æö
÷
ç
-+¥
÷
ç
÷
ç
èø
.
C.Hàmsốnghịchbiếntrênkhoảng
()
3;+¥ .
D.Hàmsốđồngbiếntrênkhoảng
()
;3-¥
.
Câu10.
Cho hàm số
()
yfx= có bảng biến thiên như hình vẽ. Khẳng định nào dưới đây là khẳng
định
sai?
A.Điểmcựcđạihàmsốlà
3x = . B.Giátrịcựcđạicủahàmsốlà 27 .
C.Giátrịl ớnnhấtcủahàmsốlà
27 . D. 0x = làmộtđiểmcựctrịcủahàmsố.
Câu11.
Cho hàm số
42
cos sinyxx=+. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng ?
A.
1
4
. B.
3
4
. C.
5
4
. D.
7
4
.
Câu 12. Biếtrằngđườngthẳng
1yx=-cắtđồthịhàmsố
21
1
x
y
x
-
=
+
tạihaiđiểmphânbiệt
()
;
AA
A
xy
,
()
;
B
B
Bx y
và
AB
x
x> .Khiđó,tínhgiátrịcủabiểuthức
2
2
AB
Py y=-
.
A.
4P =- . B. 1P =- . C. 4P = . D. 3P = .
Câu13.
Cho hàm số
3
2yx x=-. Hệ thức liên hệ giữa giá trị cực đại
CD
y và giá trị cực tiểu
CT
y là:
A. 2
CT CD
yy= . B.
3
2
CT CD
yy= . C.
CT CD
yy= . D. 0
CT CD
yy+=.
Câu 14.
Đồ thị hàm số
2
39
4
x
y
x
có mấy đường tiệm cận ?
A. 1. B. 2. C. 4. D. 3.
x
'y
y
-¥
1
2
-
3
+¥
+
+
0
-
-¥
+¥
-¥
4
-¥
x
-¥
+¥
0
3
0
0
'y
y
+
+
-
-¥
27
0
-¥
Câu 15. Tìm giá trị cực đại
CÑ
y
của hàm số
2
3
.
1
x
y
x
A.
3.
B. 7. C. 10. D. 5.
Câu16.Hàmsốnàosauđâycóbảngbiếnthiênnhưhìnhbêndưới:
A.
39
2
x
y
x
-
=
-
. B.
37
2
x
y
x
-
=
-
. C.
31
2
x
y
x
-
=
-
D.
38
2
x
y
x
-
=
-
.
Câu17.Đườngthẳng
8yx=+làtiếptuyếntạiđiểmnàocủađồthịhàmsố
1
3
x
y
x
-
=
+
?
A.
()
3; 5- . B.
()
1; 1-- . C.
()
1; 1- . D.
()
5;3- .
Câu18.Khẳngđịnhnàosauđâyđúngvềhàmsố
32
2yx x x=- +
?
A.Hàmsốchỉđồngbiếntrênkhoảng
1
;
3
æö
÷
ç
-¥
÷
ç
÷
ç
èø
.
B.Hàmsốchỉđồngbiếntrênkhoảng
()
1; +¥
.
C. Hàmsốđồngbiếntrênkhoảng
1
;1
3
æö
÷
ç
÷
ç
÷
ç
èø
.
D. Hàmsốđồngbiếntrêncáckhoảng
1
;
3
æö
÷
ç
-¥
÷
ç
÷
ç
èø
và
()
1; +¥ .
Câu19.Tìmgiátrịnhỏnhấtcủahàmsố
2
73cos sin
2cos
x
x
y
x
+-
=
+
.
A.4. B.
10
3
. C.3. D.
5
3
.
Câu20.Đồthịhàmsố
32
3yx x axb=- ++cóđiểmcựctiểu
()
2; 2A - .Tính ab+ :
A.
1
. B.
2
. C.
3
. D.
4
.
Câu21.Vớigiátrịnàocủa
m
thìphươngtrình
42
230xxm-+ ++=có2nghiệmphânbiệt:
A.
3m =-
. B.
()
{
}
3; 4m Î- +¥È- . C.
()
;3m Î-¥- . D.
4m =-
.
Câu22.Đồthịhàmsố
42
yaxbxc=++với ,0ab> cómấyđiểmcựctrị?
A.
0 . B. 1. C. 2 . D.3 .
Câu23.Chohàmsố
322
342=- + -yx mx m .Tìm m đểđồthịhàmsốcóhaiđiểmcựctrị , AB
saocho
()
1; 0I
làtrungđiểmcủa
A
B
:
A.
2m =
. B.
1=-m
. C.
1=m
. D.
0m =

Câu24.Điềukiệncủa
, , abcđểhàmsố
3
yax bxc=++luônnghịchbiếntrên là:
A.
0,ab c>"Î . B. 0, 0,ab c<£"Î .C. 0,ab c<"Î .D. 0, 0,ab c>³"Î .
Câu 25.
Hàm số
2
33
2
xx
y
x

nghịch biến trên khoảng nào ?
A. 2.x  B. (;3). C. (1; ). D. (3;2).
-
-
y
x
'y
-¥
+¥
2
-¥
+¥
3
3
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1. Hàm số
2
33
2
xx
y
x

nghịch biến trên khoảng nào ?
A.
(1; ).
B.
(;3).
C.
(3;2).
D. 2.x 
Câu 2.
Cho hàm số
ax b
y
cx d

0, 0 .cadbc Khẳng định nào dưới đây là sai ?
A. Đồ thị luôn có một tiệm cận đứng.
B. Trong mọi trường hợp, trục tung không thể là tiệm cận đứng của đồ thị hàm số.
C. Đồ thị hàm số luôn có một tâm đối xứng.
D. Đồ thị luôn có một tiệm cận ngang.
Câu 3.Hàmsố 
32
334yx x x cóbaonhiêucựctrị?
A.2. B.1. C.0. D.3.
Câu 4.
Tìm giá trị nhỏ nhất của hàm số 5cos cos5yxx trên đoạn ;.
44



A.
;
44
min 4.y





B.
;
44
min 3 2.y




C.
;
44
min 3 3.y




D.
;
44
min 4.y




Câu 5.
Biết rằng đồ thị hàm số
2
83yx x cắt đồ thị hàm số
32
2394yx x x tại điểm duy
nhất
.
M
Khẳng định nào dưới đây là khẳng định đúng ?
A. Điểm
M
thuộc góc phần tư thứ hai. B. Điểm
M
thuộc góc phần tư thứ nhất.
C. Điểm
M
thuộc góc phần tư thứ ba. D. Điểm
M
thuộc góc phần tư thứ tư.
Câu 6. Tìm
m
sao cho đồ thị hàm số
32
() 2 3( 1) 6 (1 2 )
f
xx mxm mx có điểm cực đại và cực
tiểu nằm trên đường thẳng 4 .yx
A. 1.m  B. 2.m C. 1.m D. 2.m 
Câu 7.
Tìm khoảng cách d giữa hai tiệm cận đứng của hai đồ thị hàm số sau:

3
32
82
()
3
xx
f
xC
x

và

1
() '.
2
x
g
xC
x
A. 4.d B. 2.d C. 3.d D. 1.d
Câu 8.Đồthị ở hình bên làđồthị của
hàmsốnàotrongbốnhàmsốdướiđây?
A.
42
21yx x=- +
 .
B.
42
21yx x=- + - .
C.
42
21yx x=- - + .
D.
42
21yx x=+ - .
x
y
O
Câu9.Khoảngnghịchbiếncủahàmsố
32
15
3
33
yxxx=--+là:
A.
()
;1-¥ -
.B.
()
1; 3-
. C.
()
3;+¥
. D.
()
;1-¥ -
và
()
3;+¥
.
Câu10.Giátrịnhỏnhấtcủahàmsố
2
2
yx
x
=+
với 0x > bằng:
A.4. B.3. C.1. D.2.
Câu 11. Chohàm số
()
()
2
1=- + +yx xmxm. Tìm m đểđồthị hàmsố cắt trục hoành tạiba
điểmphânbiệt.
A.
4.m >
 B.
1
0.
2
m-¹ <
 C.
04.m<<
 D.
1
0
.
2
4
m
m
é
ê
-¹ <
ê
ê
>
ê
ë

Câu12.Hàmsố
32
1yax ax=-+
cóđiểmcựctiểu
2
3
x =
khiđiềukiệncủa
a
:
A.
2a =
. B. 0a > . C.
0a =
. D. 0a < .
Câu13.Chođườngcong
()
2
:
2
-
=
+
x
Cy
x
.Điểmnàodướiđâylàgiaocủahaitiệmcậncủa
()
C
?
A.
()
2;2-L . B.
()
2;1M . C.
()
2; 2--N . D.
()
2;1-K .
Câu 14.
Cho bảng biến thiên sau:
Biết đây là bảng biến thiên của hàm số
42
.yax bx Tìm giá trị của
a
và
.b
A.
1a
và
2.b 
B.
2a
và
3.b 
C.
1a 
và
2.b
D.
1a 
và
2.b 
Câu 15.
Với bài toán tìm tất cả các giá trị thực của m sao cho hàm số
2
21
2
x
mx
y
x
m

đạt cực đại
tại
1,x
một học sinh đã tiến hành giải như sau:
Bước 1. Tập xác định
\2Dm
và tính

22
2
441
'.
2
xmxm
y
xm

Bước 2. Hàm số đạt cực đại tại
1
x

'1 0.y
Bước 3. Biến đổi


2
0
4(1 )
'1 0 0
1
12
m
mm
y
m
m
 
Kết luận
0, 1mm
thỏa mãn bài toán.
Học sinh giải đúng hay sai, nếu sai thì sai ở bước nào ?
A. Học sinh giải sai và sai ở bước 1. B. Học sinh giải sai và sai ở bước 3.
C. Học sinh giải sai và sai ở bước 2. D. Học sinh giải đúng.
Câu 16. Tìm giá trị lớn nhất, nhỏ nhất của hàm số

32
3935fx x x x
trên đoạn
4; 4 .
A.




4;4
4;4
max 15; min 41.fx fx

B.




4;4
4;4
max 8; min 41.fx fx

C.


4;4
4;4
max 40; min 41.fx fx

D.




4;4
4;4
max 40; min 8.fx fx

Câu 17.
Biết rằng đồ thị hàm số
3
31yx x cắt đồ thị hàm số
2
3yx tại điểm duy nhất, kí hiệu
00
;
x
y
là tọa độ điểm đó. Tìm
0
.y
A.
0
3.y B.
0
4.y C.
0
2.y D.
0
5.y
Câu 18.
Trong các hàm số dưới đây, hàm số nào có tiệm cận đứng ?
A.

2017
2
.
3
fx x x
B.

1
3.
3
fx x
x

C.

2
1
.
1
x
fx
x
D.

42
2017.fx x x
Câu 19. Đồ thị ở hình bên là đồ thị của hàm số nào
trong bốn hàm số dưới đây?
A.
32
11
23
33
yxxx=-+-
.
B.
32
11
23
33
yxxx=- + - -
.
C.
32
11
34
33
yxx x=-+-
.
D.
32
691yx x x=- +-.
x
1
1
3
-
y
1
O
3
Câu20.
Tìm tất cả giá trị của số thực m để hàm số
()
32
1
21 2
3
yxmx mxm=-+--+
đồng biến trên .
A. 1m > . B. 1m = . C. 1m ¹ . D. 1m < .
Câu21.Chohàmsố
42
1yax bx=-+xácđịnhvàliêntụctrên vàcóbảngbiếnthiên:
Giátrịcủa
a vàb thỏađềbàilà:
A.
1a = và 2b = . B. 1a =- và 4b =- . C. 1a = và 4b = .D. 1a =- và 2b =- .
Câu22.Sốđiểmcótọađộlàcácsốnguyêntrênđồthịhàmsố
3
2
x
y
x
-
=
-
là:
A.
6
. B. 2 . C. 4 . D.
8
.
Câu23.Chohàmsố
42
231yx mx m=- +-.Khẳngđịnhnàosauđâysai?
A.Hàmsốcó1cựctrịkhi
0m £ . B.Hàmsốcó3cựctrịkhi 0m > .
C.Hàmsốcó1cựctrịkhi
0m <
. D.Hàmsốcóítnhấthaicựctrị.
Câu24.Đồthịcủahàmsố
32
yax bx cxd=+++cóhaiđiểmcựctrịlàgốctọađộ
()
0;0O
vàđiểm
()
2; 4A - thìphươngtrìnhcủahàmsốlà:
A.
32
3yx x=- . B.
3
3yx x=-. C.
32
3yxx=- + . D.
3
3yxx=- + .
Câu 25:
Số điểm cực trị của đồ thị hàm số
3
1
7
3
yxx
là ?
A. 1 B. 0 C. 3 D. 2
x
'y
y
-¥
2-
0
2
+¥
0
0
0
-
+
-
+
1 b-
+¥
a
1 b-
+¥
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1:
Đồ thị hàm số sau là của hàm số nào?
A.
32
31yx x B.
42
22yx x
C.
42
22yx x D.
32
31yx x
Câu 2:
Số điểm cực trị của đồ thị hàm số
3
1
7
3
yxx là ?
A. 1 B. 0 C. 3 D. 2
Câu 3: Cho hàm số sau:
1
3
x
y
x
, những mệnh đề nào đúng trong các mệnh đề sau ?
(1) : Hàm số luôn nghịch biến trên
\3D
(2) : Đồ thị hàm số có 1 tiệm cận đứng là
1
x
; 1 tiệm cận ngang là 3y
(3) : Hàm số đã cho không có cực trị.
(4): Đồ thị hàm số nhận giao điểm
3;1I của 2 đường tiệm cận làm tâm đối xứng.
A. (1),(3),(4) B. (3),(4) C. (2),(3),(4) D. (1), (4)
Câu 4: Hàm số
2
1
x
y
x
đồng biến trên khoảng nào ?
A.

;1 B.

1;  C.

1;1 D.

;1 và
1; 
Câu 5: Cho hàm số
42
22yx x . Giá trị cực đại của hàm số bằng ?
A. 2 B. 1 C. -1 D. 0
Câu 6: Tìm giá trị nhỏ nhất của hàm số
32
396yx x x  trên

4; 4
A.

4;4
21Min f x
B.

4;4
14Min f x
 C.

4;4
11Min f x
D.

4;4
70Min f x

Câu 7: Tìm m để hàm số
2
3
3
x
mx
y
x
(C) cắt đường thẳng
7ymx d
tại 2 điểm phân biệt?
A.
19
12
m
B.
19
12
m và
1m C.
19
12
m
D.
19
12
m và
1m
Câu 8: Đồ thị hàm số
2
2
21
2
x
y
x
x
có bao nhiêu tiệm cận ?
A. 1 B. 0 C. 2 D. 3
Câu 9. Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn đáp án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A.
2
1.yxx B.
3
51.yx x C.
42
23.yx x D.
42
23.yx x
Câu 10. Hàm số
32
21
y
xxx đồng biến trên khoảng nào ?
A.
1
;
3




và
1;  . B.
2
;.
3




C.

;1 và

2; . D.
1
;1 .
3



Câu 11. Cho hàm số
()
y
fx
xác định và liên tục trên
và có bảng biến thiên sau:
Khẳng định nào sau đây là khẳng định
sai ?
A. Hàm số có ba cực trị. B. Hàm số đạt giá trị cực đại tại
1
x

và
2.
x
C. Hàm số đạt giá trị cực đại tại 1.
x
D. Giá trị cực đại của hàm số
16
.
3
CÑ
y
Câu 12. Cho hàm số

2
23
.
2
xx
fx
x

Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số luôn nghịch biến trên
.
B. Hàm số luôn nghịch biến trên
\2.
C. Hàm số luôn đồng biến trên . D. Hàm số đồng biến trên khoảng
;2 và
2; .
Câu 13. Cho hàm số
2
1
x
ax b
y
x

với , ab là các số thực. Đồ thị hàm số đã cho có điểm cực đại
là
(0; 1).A
Tính giá trị của biểu thức
2.Pab
A.
3.P
B.
6.P
C.
5.P
D.
4.P
Câu 14.
Tìm đường tiệm cận ngang của đồ thị hàm số
2
3
.
1
x
y
x
A. 3.
y
B. 2.
y
C. 1.
y
D.
1
.
2
y
Câu 15.
Tìm giá trị nhỏ nhất của hàm số
2
2
20 10 3
321
xx
y
xx


trên đoạn
3; 1 .



A.
7.
B.
13
.
2
C.
153
.
22
D. 6.
Câu 16.
Biết rằng đường thẳng
y
x cắt đồ thị hàm số
4
3
x
y
x
tại điểm duy nhất, kí hiệu điểm đó
là

00
;.
x
y Tìm
0
.
y
A.
0
4.y B.
0
6.y C.
0
2.y D.
0
1.y 
Câu 17.
Cho hàm số
32
26yx x x
, khẳng định nào sau đây đúng về tính đơn điệu của hàm số:
A. Hàm số đồng biến trên
;1 và
1
;
3




B. Hàm số chỉ nghịch biến trên
1
;
3




C.
Hàm số đồng biến trên
1
1;
3



D. Hàm số nghịch biến trên

;1 và
1
;
3




Câu 18. Cho hàm số

2
3
2
x
yfx
x

có đồ thị (C). Khẳng định nào sau đây là đúng?
A. Đồ thị (C) có một tiệm cận đứng là
2x
và không có tiệm cận ngang
B.
Đồ thị (C) có đúng một tiệm cận đứng là 2x và một tiệm cận ngang là 0y .
C. Đồ thị (C) có hai tiệm cận đứng là 2; 2xxvà một tiệm cận ngang là 0y .
D. Đồ thị (C) có hai tiệm cận đứng là 2; 2xxvà không có tiệm cận ngang.
Câu 19. Hàm số
32
29124yx x x nghịch biến trên khoảng nào?
A.
;1
B.
1; 2
C.
2;3
D.
2; 
Câu 20. Trong các hàm số sau hàm số nào đồng biến trên ?
A.
3sin 1 4
y
x B.
2
34yxx C.
42
1yx x D.
3
513yx x
Câu 21. Cho hàm số
42
243yx x và các kết quả sau:
(I):
3
CT
y 
tại 0x (II):
3
CD
y
tại 1x  (III):
3
CD
y
tại 1
x
Kết luận nào đúng:
A. Chỉ I B. Chỉ II C. Chỉ III D. Cả I, II, III
Câu 22. Tìm giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn

2; 4
A.

2;4
min 6y B.

2;4
min 2y  C.

2;4
min 3y  D.

2;4
19
min
3
y
Câu 23. Tìm giá trị nhỏ nhất của hàm số
53
2
x
y
x
trên
3; 5
A.

3;5
28
min
3
y
B.

3;5
3
min
2
y
 C.

3;5
min 2y  D.

3;5
min 5y
Câu 24. Cho đồ thị của hàm số
42
yax bx c ( 0)a như hình vẽ. Khẳng định nào sau đây là
khẳng định
đúng ?
A. 0, 0, 0.abc B. 0, 0, 0.abc C. 0, 0, 0.abc D. 0, 0, 0.abc
Câu 25.
Tìm các khoảng đồng biến của hàm số
21
.
2
x
y
x
A.
;2 và
2;  . B.
1
;
2




và
1
;.
2




C.
1
;
2




và
1
;.
2




D.
;2 và
2; .
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1.
Số điểm cực trị của hàm số
32
yax bx cxd ( 0)a có thể là ?
A. 3. B.
0
hoặc
2.
C. 1 hoặc
2.
D.
0
hoặc 1 hoặc
2.
Câu 2. Tìm giá trị nhỏ nhất của hàm số

2
4
1sin2 .
sin 2
fx x
x

A. 3. B.
15.
C.
17.
D. 4.
Câu 3. Điểm
M
thuộc đồ thị
C của hàm số
2
515
3
xx
y
x

và
M
có tọa độ là các số nguyên.
Hỏi có bao nhiêu điểm
M
thỏa mãn bài toán ?
A. 4 B. 7. C. 3. D. 6
Câu 4.
Cho hàm số

32
1
21 1
3
yxmx mx
. Mệnh đề nào sau đây là sai ?
A. 1m thì hàm số có hai cực trị B. Hàm số luôn luôn có cực đại và cực tiểu.
C.
1m thì hàm số có cực đại và cực tiểu. D. 1m thì hàm số có cực trị.
Câu 5. Tập xác định của hàm số
21
3
x
y
x
là:
A.
D
B.
;3D  C.

;3\
1
2
D



D.
3;D 
Câu 6. Tìm m để đồ thị hàm số
2
1
234
x
y
xmxm

có đúng một đường tiệm cận đứng
A.
5; 1; 4m  B.
1; 4m  C.
;1 4;m  D.
1; 4m 
Câu 7. Hàm số
32
29124yx x x nghịch biến trên khoảng nào ?
A.
;1 B.
1; 2 C.
2;3 D.
2; 
Câu 8. Đồ thị hàm số
32
6136yx x x có bao nhiêu điểm cực trị ?
A. 0 B. 1 C. 2 D. 3
Câu 9. Với giá trị nào của m để đường thẳng yxm đi qua trung điểm của đoạn nối hai điểm cực
trị của đồ thị hàm số
32
69yx x x ?
A. 0m B. 1m C. 2m D. 3m
Câu 10. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
31yx x trên đoạn
1; 4 là:
A.


1;4
1;4
max 51;min 3yy
 B.


1;4
1;4
max 51;min 1yy

C.


1;4
1;4
max 51;min 1yy

D.


1;4
1;4
max 1;min 1yy

Câu 11. Cho hàm số
()yfx
có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị hàm số có tiệm cận đứng 1y  và tiệm cận ngang
2.x 
B. Đồ thị hàm số có duy nhất một tiệm cận.
C. Đồ thị hàm số có ba tiệm cận.
D. Đồ thị hàm số có tiệm cận đứng
1x 
và tiệm cận ngang 2.y 
Câu 12. Hàm số
2
1
1
x
x
y
x

nghịch biến trên khoảng nào ?
A.
;1 .
B.
1; 2 .
C.
2; .
D.
;0 .
Câu 13.
Kí hiệu m và
M
lần lượt là GTNN, GTLN của hàm số
2
12 3 .yx x Tính tỉ số .
m
M
A.
1
.
4
m
M

B.
1
.
2
m
M
C.
1
.
2
m
M

D.
1
.
4
m
M
Câu 14.
Số giá trị cực trị của hàm số
42
23yx x
là:
A. 1 B. 2 C. 3 D. Vô số
Câu 15. Giá trị lớn nhất của hàm số
32
24yx x x là:
A. -4 B.
104
27
C. 100 D. Không tồn tại
Câu 16. Số điểm cực trị của hàm số
32
336yx x x là:
A. 0 B. 1 C. 2 D. Vô số
Câu 17. Chọn phát biểu đúng khi nói về tiệm cận của đồ thị hàm số
21
2
x
y
x
.
A. Tiệm cận ngang là đường thẳng 2y  B. Tiệm cận đứng là đường thẳng
2x
C. Tiệm cận đứng là đường thẳng 2y D. Tiệm cận ngang là đường thẳng 2y
Câu 18. Khoảng đồng biến của hàm số
32
1
235
3
yxxxlà:
A.

;3
B.
1; 
C.

1; 3
D.

3; 
Câu 19. Tâm đối xứng của đồ thị hàm số
32
11
23
33
yxxx có tọa độ là:
A.
1
2;
3
I



B.
1
2;
3
I



C.
1
2;
3
I



D.
1
2;
3
I




Câu 20. Hàm số nào dưới đây có bảng biến thiên sau:
x

0
2

'y
0
0
y
CÑ
y


3
A.
32
31.yx x B.
32
31.yx x
C.
42
43.yx x D.
32
264.yx x
Câu 21.
Đồ thị hàm số nào sau đây không có ba tiệm cận ?
A.
2
3
.
22
x
y
x
x
B.
2
2
1
.
4
xx
y
x

C.
3
3
1
.
1
xx
y
x

D.
3
32
2
34
x
y
xx

.
Câu 22.
Cho hàm số

1
.
25
x
fx
x
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số luôn nghịch biến trên
.
B. Hàm só luôn nghịch biến trên hai khoảng
2
;
5




và
2
;.
5




C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên hai khoảng
2
;
5




và
2
;.
5




Câu 23. Cho hàm số

22.fx x x Khẳng định nào sau đây là khẳng định đúng ?
A.


2;2
min 0fx
và


2;2
max 3 2.fx
B.


2;2
min 2fx
và


2;2
max 3 2.fx
C.


2;2
min 2fx
và


2;2
max 2 2.fx
D.

2;2
min 1fx
và


2;2
max 3 2.fx
Câu 24.
Giao điểm hai đường tiệm cận của đồ thị hàm số
3
3
32
3
xx
y
x

có tọa độ là ?
A.
3
1; 3 .T B.
3
3;1 .T C.
1; 3 .T
D.
3;1 .T
Câu 25.
Tìm tất cả giá trị thực của tham số
m
sao cho hàm số
32
3 3 20 17yx x mx m
đồng
biến trên
.
A.
;.m 
B.
1; .m 
C.
1; .m

D.
;1 .m

SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1. Hàm số
21
1
x
y
x
luôn:
A. Đồng biến trên B. Nghịch biến trên
C. Đồng biến trên từng khoảng xác định D. Nghịch biến trên từng khoảng xác định
Câu 2. Giá trị cực đại của hàm số
32
357yx x x là:
A.
326
3

B.
326
3

C.
32 6
9
D.
32 6
9
Câu 3: Khoảng đồng biến của hàm số
2
xx2
y
x1

là:
A.

;3 và

1;  B.
;1 và
3;  C.

3;  D.
1; 3
Câu 4: Đường thẳng
d:y x 3
cắt đồ thị (C) của hàm số
4
y2x
x

tại hai điểm. Gọi
12 1 2
x,x x x là hoành độ giao điểm của hai đồ thị hàm số, tính
21
y3y .
A.
21
y3y25 B.
21
y3y 10 C.
21
y3y1 D.
21
y3y 27
Câu 5. Một vật rơi tự do với phương trình chuyển động
2
1
2
Sgt
, trong đó
2
9,8 /
g
ms và t tính
bằng giây (
s). Vận tốc của vật tại thời điểm
5
ts
bằng:
A. 25 /ms B. 49 /ms C. 10 /ms D. 18 /ms
Câu 6. Hàm số
21
1
x
y
x
luôn:
A. Đồng biến trên B. Nghịch biến trên
C. Đồng biến trên từng khoảng xác định D. Nghịch biến trên từng khoảng xác định
Câu 7. Hàm số
2
323
y
mxmx không có cực trị khi:
A.
3m
B.
0
3
m
m
C.
0m
D.
3m
Câu 8. Hàmsốnàosauđâyđồngbiếntrên ?
A.
tanyx. B. 
42
2yxx. C. 
3
31yx x . D. 
3
2yx .
Câu 9.
Gọi Q là giá trị lớn nhất và K là giá trị nhỏ nhất của hàm số
2
1
1
x
y
x
trên đoạn
1; 2 . Khi đó
giá trị của biểu thức
24 27
1997
2
QK
là:
A.
3929
2
B.
3925
2
C.
3927
2
D.
3923
2
Câu 10: Đồ thị hàm số nào sau đây luôn nằm dưới trục hoành
A.
42
yx 3x 1
B.
32
yx2xx1
C.
42
yx2x2
D.
42
yx4x1
Câu 11: Khoảng đồng biến của hàm số
2
xx2
y
x1

là:
A.
;3 và
1;  B.

;1 và

3;  C.

3;  D.
1; 3
Câu 12: Đường thẳng
d:y x 3 cắt đồ thị (C) của hàm số
4
y2x
x
 tại hai điểm. Gọi
12 1 2
x,x x x
là hoành độ giao điểm của hai đồ thị hàm số, tính
21
y3y .
A.
21
y3y1
B.
21
y3y 10
C.
21
y3y25
D.
21
y3y 27
Câu 13: Tính tất cả các giá trị của tham số m để hàm số

32
1
ym1xx2m1x3
3
 có cực
trị ?
A.
3
m;0
2




B.

3
m;0\1
2




C.
3
m;0
2




D.

3
m;0\1
2




Câu 14. Kết luận nào sau đây là không đúng về đồ thị hàm số
32
0yax bx cxda ?
A. Đồ thị hàm số bậc ba luôn cắt trục hoành tại ít nhất một điểm.
B.
Đồ thị hàm số bậc ba nhận điểm có hoành độ là nghiệm của PT "0y làm tâm đối xứng.
C.
Nếu PT '0y có 2 nghiệm phân biệt thì đồ thị hàm số bậc ba có 1 điểm cực đại, 1 điểm cực
tiểu.
D.
Đồ thị hàm số bậc ba không có điểm cực trị khi và chỉ khi phương trình ' 0y vô nghiệm.
Câu 15. Hàm số
2
31
1
x
x
y
x

đồng biến trên:
A.
;1
và
1;
B.

;1 1; 
C. đồng biến với mọi
x
D.

1;1
Câu 16. Cho đồ thị hàm số
42
23yfx x x như hình vẽ. Từ đồ thị suy ra được số nghiệm của
phương trình
42
23
x
xm với
3; 4m là:
A. 3 B. 2 C. 4 D. 6
Câu 17.
Biết đồ thị hàm số
42
yx bx c chỉ có một điểm cực trị là
điểm có tọa độ

0; 1 thì
b
và
c
thỏa mãn điều kiện nào ?
A. 0b và 1c  B. 0b và 1c  C. 0b và 0c D. b và c tùy ý.
Câu 18. Với giá trị nào của
m
thì đường thẳng yxm đi qua trung điểm của đoạn nối 2 điểm cực
trị của đồ thị hàm số
32
69yx x x ?
A. 0 B. 1 C. 2 D. 3
Câu 19. Gọi
M
và
m
lần lượt là GTLN và GTNN của hàm số
2
1yx x trên tập xác định. Khi
đó
M
m
bằng ?
A. 1 B. 2 C. 3 D. đáp số khác
Câu 20. Đồ thị của hàm số
3
3yx x cắt:
A. đường thẳng 3y tại hai điểm B. đường thẳng 4y  tại hai điểm.
C.
đường thẳng
5
3
y tại ba điểm D. trục hoành tại một điểm.
Câu 21: Cho hàm số
yfx xác định, liên tục trên
và có bảng biến thiên:
x
 1 1 2 
y
' + 0 + 0 - 0 +
y
9
20


3
5
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có ba cực trị.
B. Hàm số có giá trị lớn nhất bằng
9
20
và giá trị nhỏ nhất bằng
3
5
C. Hàm số đồng biến trên khoảng
;1
D. Hàm số đạt cực đại tại x 2 và đạt cực tiểu tại x 1
Câu 22: Đồ thị hàm số
x1
y
x1
có bao nhiêu đường tiệm cận ?
A. 0 B. 1 C. 2 D. 3
Câu 23: Cho hàm số
3
yx 3x1
. Viết phương trình đường thẳng qua hai điểm cực trị của đồ thị
hàm số.
A. y 2x 1 B. y 2x 1 C. y 2x 1 D. y 2x 1
Câu 24: Đồ thị hàm số bậc 2 và đồ thị hàm số bậc 4 trùng phương có chung đặc điểm nào sau đây
A. Đều tồn tại cả điểm cực đại và điểm cực tiểu B. Đều có tâm đối xứng
C. Đồ thị hàm số đều có dạng parabol D. Đều có trục đối xứng
Câu 25: Hàm số
42
21 yx x
A. Nghịch biến trên ( -1 ; 1) B. Đồng biến trên
(1; )
C. Đồng biến trên
(;0) D. Nghịch biến trên (-1 ; 0)
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1: Tổng của GTLN và GTNN của hàm số
32
3935yx x x trên đoạn


4;4 là :
A. -1 B. 48 C. -26 D. 23
Câu 2: Hãy xác định a,b để hàm số
2ax
y
x
b
có đồ thị như hình vẽ:
A. 1 ; 2ab B.
2ab
C. 1; 2ab D.
2
ab
Câu 3: Giá trị nhỏ nhất của hàm số y = sinx( 1 + cosx) trên đoạn [ 0;
] là:
A.
1 B.
2
2
C. 0 D.
3
4
Câu 4:
Phương trình tiếp tuyến của đồ thị
2
2x 1
y
x
tại điểm có hoành độ x 1 là:
A. y x 2 B. y 3x 3 C. y x 2 D. y x 3
Câu 5: Giá trị lớn nhất của hàm số
2
fx x 2x 3
trên đoạn
0;3
là:
A. 3 B. 18 C. 2 D. 6
Câu 6: Giá trị nhỏ nhất của hàm số

2
fx x 2x 5 là:
A. 5 B. 22 C. 2 D. 3
Câu 7: Giá trị lớn nhất và GTNN của hàm số
32
3940yx x x trên đoạn

5;5 lần lượt là
A. 45; 115 . B. 13; 115 . C. 45;13. D. 115;45 .
Câu 8: Cho hàm số
42
2 1024yx x . Trong các mệnh đề sau, mệnh đề nào sai?
A. Đồ thị hàm số qua (0; 1024)A . B. Hàm số có 1 cực tiểu.
C.
lim ( ) ; lim ( )
xx
fx fx
 
 
. D. Đồ thị có 2 điểm có hoành độ thỏa mãn
'' 0y
.
Câu 9: Tìm GTLN của hàm số
2
5yx x trên 5; 5


?
A. 5. B. 10 . C. 6. D. Đáp án khác.
Câu 10: Phương trình
32
3
x
xm m có 3 nghiệm phân biệt khi
A. 21m  . B. 12m . C. 12m . D. 21m .
Câu 11: Phương trình tiếp tuyến của đường cong (C)
3
2yx x tại điểm có hoành độ 1x  là
A.
2yx

. B.
2yx

. C.
2yx

. D.
2yx

.
Câu 12: Cho hàm số
32
61yx x mx đồng biến trên
0;  khi giá trị của m là
A. 0m . B. 0m . C. 12m . D. 12m .
Câu 13: Điểm nào sau đây thuộc đồ thị hàm số
3
35yx x mà hoành độ là nghiệm của phương
trình
'' 0y
?
A.

0;0 . B.

1; 3 . C.
1;1 . D.
0;5 .
Câu 14: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
x1
y
x2
B.
x1
y
x2


C.
2x 1
y
2x 2
D.
x1
y
x2
Câu 15: Hàm số
42
yx8x7 có bao nhiêu giá trị cực trị ?
A. 0 B. 1 C. 2 D. 3
Câu 16: Hỏi có tất cả các giá trị nguyên của m để đồ thị hàm số

32 2
1
y x mx 2m 3m 3 x 2016
3

có 2 cực trị:
A. 3 B. 4 C. 5 D. 6
Câu 17: Tìm tất cả các giá trị của m để hàm số
32
2
yxmx4mx2016
3
 có hai điểm cực trị thỏa
12
xx 3.
A. m9 B. Không tồn tại giá trị m thỏa mãn yêu cầu bài toán
C.
m1
m9

D. m1
Câu 18: Tìm tọa độ giao điểm M của đồ thị

2x 1
C:y
x1
và đường thẳng d : y 3
A.
M4;3
B.

M3;4
C.
M4;3
D.
M3; 4
Câu 19: Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số
2
x5
y
x1
A. Đồ thị hàm số không có đường tiệm cận đứng B. x 1 và x 1
C. x 1 D. x 1
Câu 20: Viết phương trình tiếp tuyến của đồ thị hàm số
42
fx x x 1
tại điểm có hoành độ x 1
A. y 6x 3 B. y 6x 3 C. y 6x 3 D. y 6x 3
Câu 21: Cho hàm số
yfx xác định và liên tục trên R và có bảng biến thiên:
x
 1 2


'
f
x
+ 0 + 0 -
f
x
5
0


Mệnh đề nào sau đây là
sai:
A. Hàm số đồng biến trên
;2 B. Hàm số nghịch biến trên
2;
C. Giá trị lớn nhất của hàm số trên R là 5 khi 2x D. Hàm số đạt cực trị tại 1x 
Câu 22: Cho hàm số
42
45yx x và các khoảng: (I)
2;0 , (II)

0; 2 , (III)

2;
Hàm số đồng biến trên khoảng nào ?
A. I và II B. II và III C. III và I D. chỉ I
Câu 23: Giao điểm có hoành độ là số nguyên của đồ thị hàm số
32yx

và đồ thị hàm số
3
1yx x là:
A.
0;1 B.
0; 2 C.

1; 5 D.

1;1
Câu 24: Tìm lỗi sai trong bài toán khảo sát hàm số
2
1
x
y
x

của một bạn học sinh như sau:
Bài giải
1. Tập xác định:
\1
2. Sự biến thiên:
+) Chiều biến thiên

2
3
'
1
y
x
y' không xác định khi
1x 
; y' luôn âm với mọi
1x 
vậy hàm số nghịch biến trên
;1
và
1;
+) Cực trị: Hàm số đã cho không có cực trị
+) Tiệm cận:
11
lim ; lim
xx
yy

 
 
Do đó đường thẳng
1x

là tiệm cận đứng
lim 1
x
y


Vậy đường thẳng 1y
 là tiệm cận ngang
+) Bảng biến thiên:
x
 1 
y
' - -
y
1

 1
A. Bài giải trên sai ở giai đoạn tìm điều kiện xác định B. Bài giải trên đạo hàm sai
C. Bài giải trên sai ở giai đoạn tìm tiệm cận D. Bài giải trên sai bảng biến thiên
Câu 25: Cho hàm số
42
361yx x. Kết luận nào sau đây là đúng ?
A. 2
CD
y  B. 1
CD
y C. 1
CD
y  D. 2
CD
y
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A
1
. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
…………………………………………….
CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13
ĐÁP ÁN
CÂU 14 15 16 17 18 19 20 21 22 23 24 25
ĐÁP ÁN
Câu 1: Tìmgiátrịnhỏnhấtcủahàmsố
2
5
3
x
y
x
trênđoạn


0;2 .
A.



0;2
5
min
3
x
y
.
B.



0;2
1
min
3
x
y
.
C.



0;2
min 2
x
y
.
D.



0;2
min 10
x
y
.
Câu 2: Cho hàm số
3
y x 3x 2016 . Trong các giá trị sau giá trị nào là giá trị cực trị của hàm số?
A. 2 B. 2018 C. 2017 D. -1
Câu 3: Tìm tọa độ điểm cực tiểu M của đồ thị hàm số
3
yx 3x2
A.

M1;0 B.

M1;0 C.

M1;4 D.
M1;4
Câu 4: Gọi M , N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
2
yx 4x .
Giá trị của biểu thức
M2N
A.
22 2
B.
22 4
C.
22 2
D.
22 4
Câu 5: Trong các kết quả sau, kết quả nào nêu đúng cả hai đường thẳng đều là tiệm cận của đồ thị
hàm số
x5
y
x1
A.
x1;y 1
B.
x1;y2 
C.
x1;y1
D.
x1;y2
Câu 6: Đồ thị hàm số
2
x 2016
y
x5
có số đường tiệm cận là:
A. 1 B. 2 C. 3 D. 4
Câu 7. Cho hàm số
yfx có đạo hàm tại
0
x
. Tìm mệnh đề đúng?
A. Nếu
0
'0fx thì hàm số đạt cực trị tại
0
x
B.
Hàm số đạt cực trị tại
0
x
thì
0
0fx
C.
Nếu hàm số đạt cực trị tại
0
x
thì
0
'0fx
D.
Hàm số đạt cực trị tại
0
x
thì
'
f
x đổi dấu khi qua
0
x
Câu 8. Một học sinh khảo sát sự biến thiên
32
11
22
32
yx xx

như sau:
I.
Tập xác định: DR
II.
Sự biến thiên:
2
1
'2;'0
2
x
yxx y
x


lim ; lim
xx
yy
 
 
III. Bảng biến thiên:
x  -1 2 
y'
+ 0
0 +
y
19
6


4
3
IV. Vậy hàm số đồng biến trên
;1 2; 
, nghịch biến trên khoảng
1; 2
Lời giải trên sai từ bước nào?
A. Lời giải trên sai từ giai đoạn I B. Lời giải trên sai từ giai đoạn II
C.
Lời giải trên sai từ giai đoạn III D. Lời giải trên sai ở giai đoạn IV
Câu 9. Xác định ,ab để hàm số
ax
y
x
b
có đồ thị như hình vẽ:
A. 2;1ab B. 1;2ab
C.
1; 2ab D. 2; 1ab 
Câu 10.
Hàm số nào sau đây không có cực trị:
A.
2
yx B.
3
3yx x C.
42
2yx x D.
2
3yx
Câu 11. Hàm số nào sau đây không có GTLN trên đoạn

2; 2
?
A.
1
2
yx

B.
3
2yx C.
42
yx x D.
1
1
x
y
x
Câu 12. Số nguyên dương m nhỏ nhất để đường thẳng
yxm
cắt đồ thị hàm số

3
:
2
x
Cy
x
tại hai điểm phân biệt là:
A. 1m B. 0m C. 2m D. 3m
Câu 13. Cho hai hàm số
2
23
4
x
y
x
m

và
7
5
x
y
x

. Tập hợp các giá trị của tham số m để hai
đường tiệm cận đứng của 2 đồ thị hàm số trên trùng nhau là?
A.
1;1
B.
3; 3
C.
2; 2
D.
0
Câu 14. Số điểm cực trị của đồ thị hàm số
42
0; 0yax bx ca b là:
A. 0 B. 2 C. 1 D. 3
Câu 15: Cho hàm số
y
fx xác định, liên tục trên R và có bảng biến thiên như sau:
x
 1 
y' + 0 +
y

1

Khẳng đinh nào đúng trong các khẳng đinh sau?
A. Hàm số đạt cực trị tại x =1 B. Hàm số đồng biến trên R
C. Tập giá trị của hàm số là
[1; )
D. Hàm số có giá trị nhỏ nhất bằng 1
Câu 16: Hàm số
3
32yx x đồng biến trên tập nào sau đây ?
A. R B. ( ; 1) C. (1; ) D. R
1
Câu 17: Đồ thị bên là đồ thị của hàm số nào trong các hàm số sau
A.
2
21yx x B.
2
21yx x
C.
42
21yx x D.
42
21yx x
Câu 18:
Tìm tổng các giá trị cực trị của hàm số
32
15
61
32
yx xx

A.
17
3
B.
11
2
C.
67
6
D.
17
3
Câu 19: Tìm giá trị lớn nhất của hàm số
2
1
42yx
x

trên đoạn [-1;2]
A. 3 B. 1 C.
29
2
D. Không tồn tại
Câu 20: Cho hàm số
21
3
x
y
x
có đồ thị (C) và đường thẳng (d) yxm . Tìm m để (C) cắt (d)
tại 2 điểm phân biệt A và B sao cho
214AB
A. -1 B. 1 C. -2 D. 2
Câu 21: Đồthịhàmsố 
32
321yx x x cắtđồthịhàmsố 
2
31yx x tạihaiđiểmphân
biệtA,B.KhiđóđộdàiABlàbaonhiêu?
A. 2AB . B. 22AB . C. 3AB . D. 1AB .
Câu 22: Tìm giá trị lớn nhất của hàm số ( ) 3cos3 2cos 2 9cos 1
f
xxxx
A. -11 B. 13 C. 16 D. -3
Câu 23: Trong các hình sau có cùng chu vi, hình nào có diện tích lớn nhất?
A. Hình tam giác đều B. Hình vuông C. Hình chữ nhật D. Hình tròn
Câu 24: Cho hàm số
42
() 2 4fx x mx m . Tìm m để đồ thị của hàm số đã cho cắt trục hoành tại
bốn điểm phân biệt.
A. 2m B. 4m C.
2
4
m
m
D. 24m
Câu 25: Tìm tiệm cận đứng của đồ thị hàm số
2
2x
y
x3x
?
A.
x0;x3
B.
y3
C.
y0
D.
x3
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN
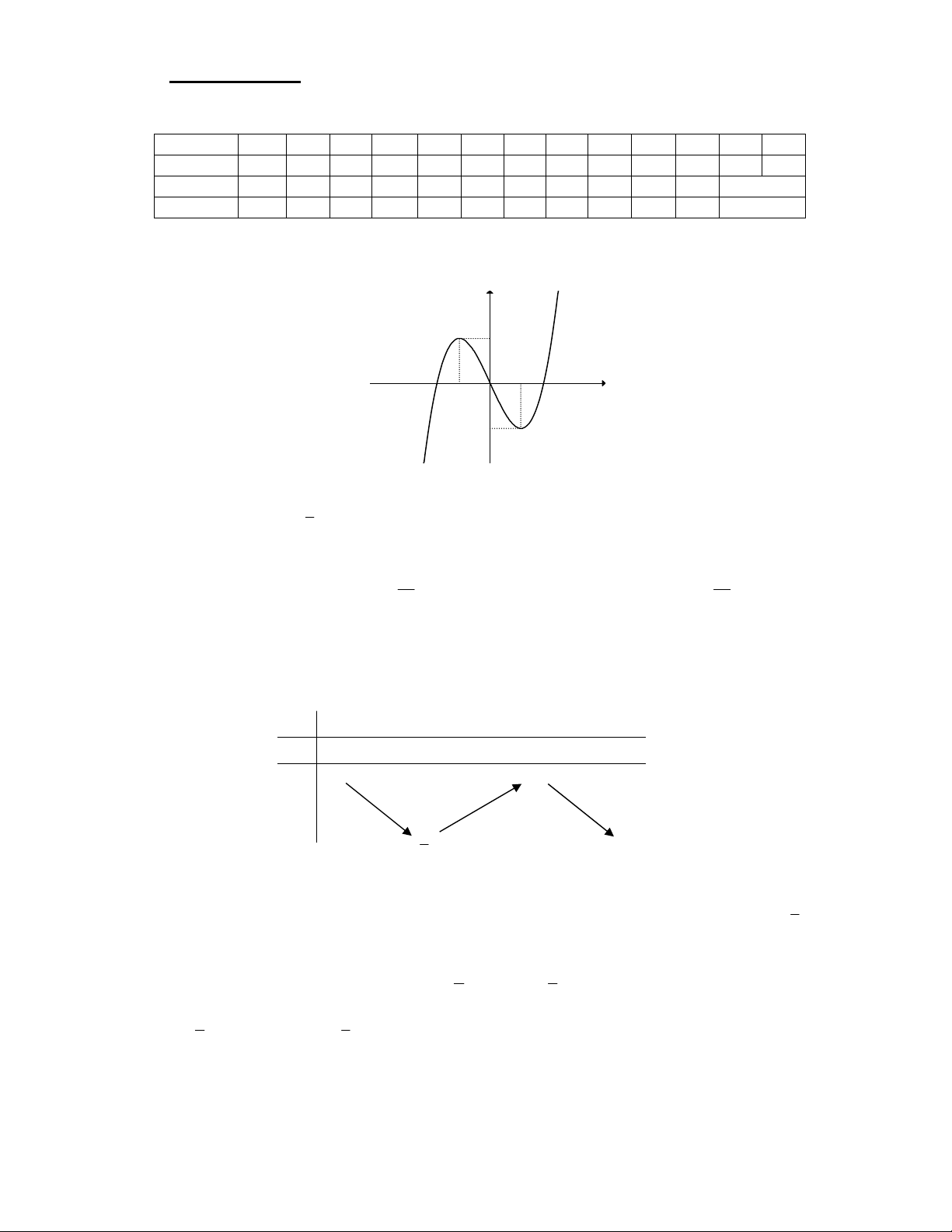
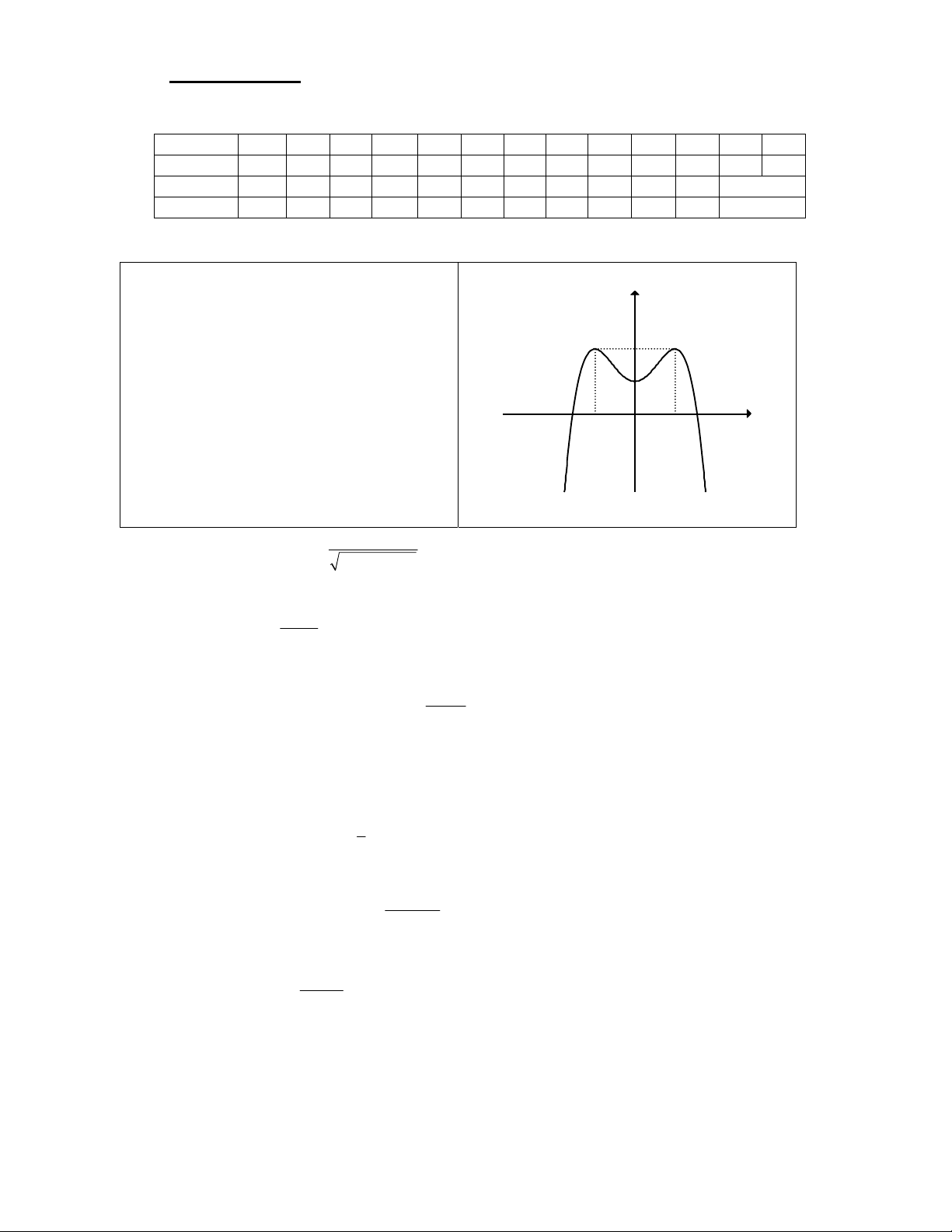
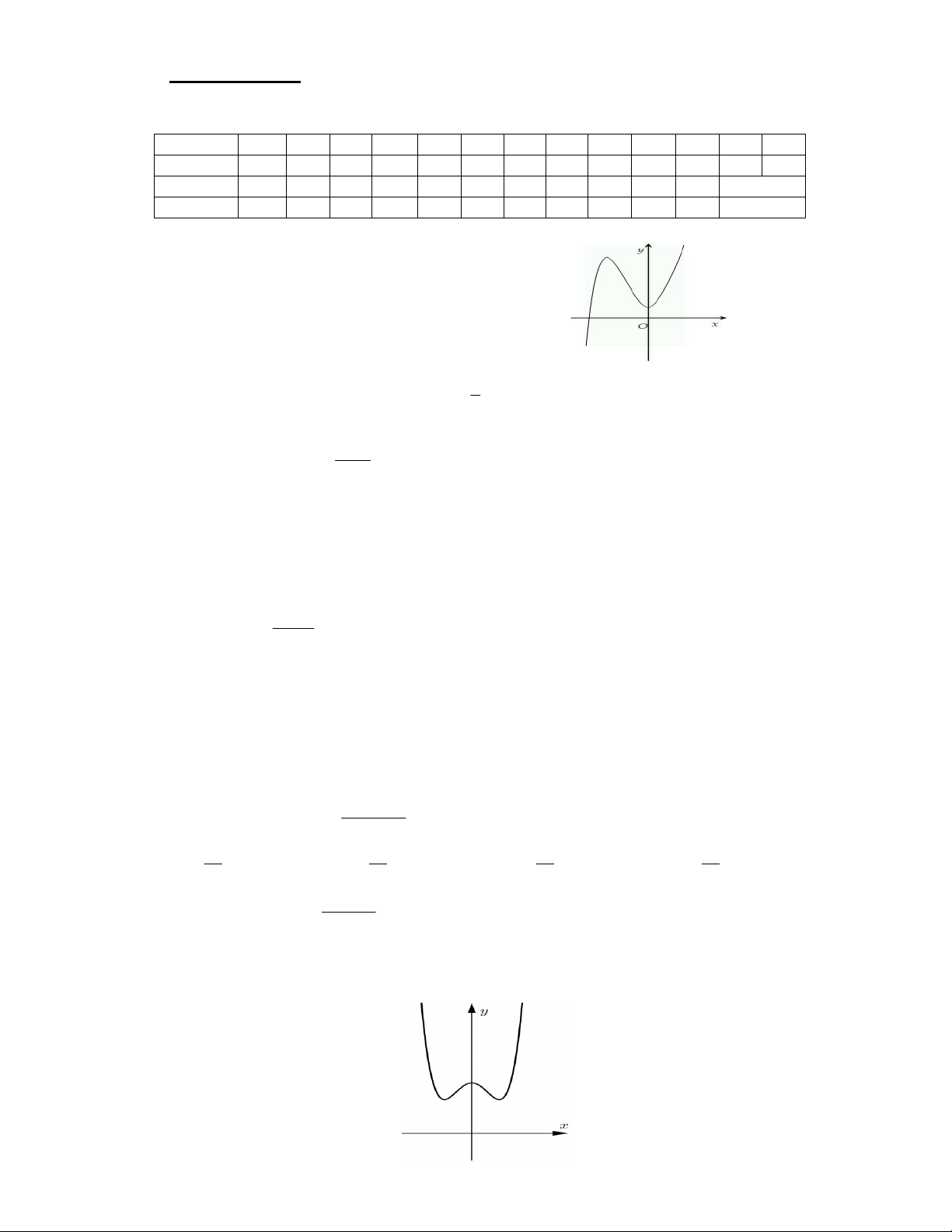
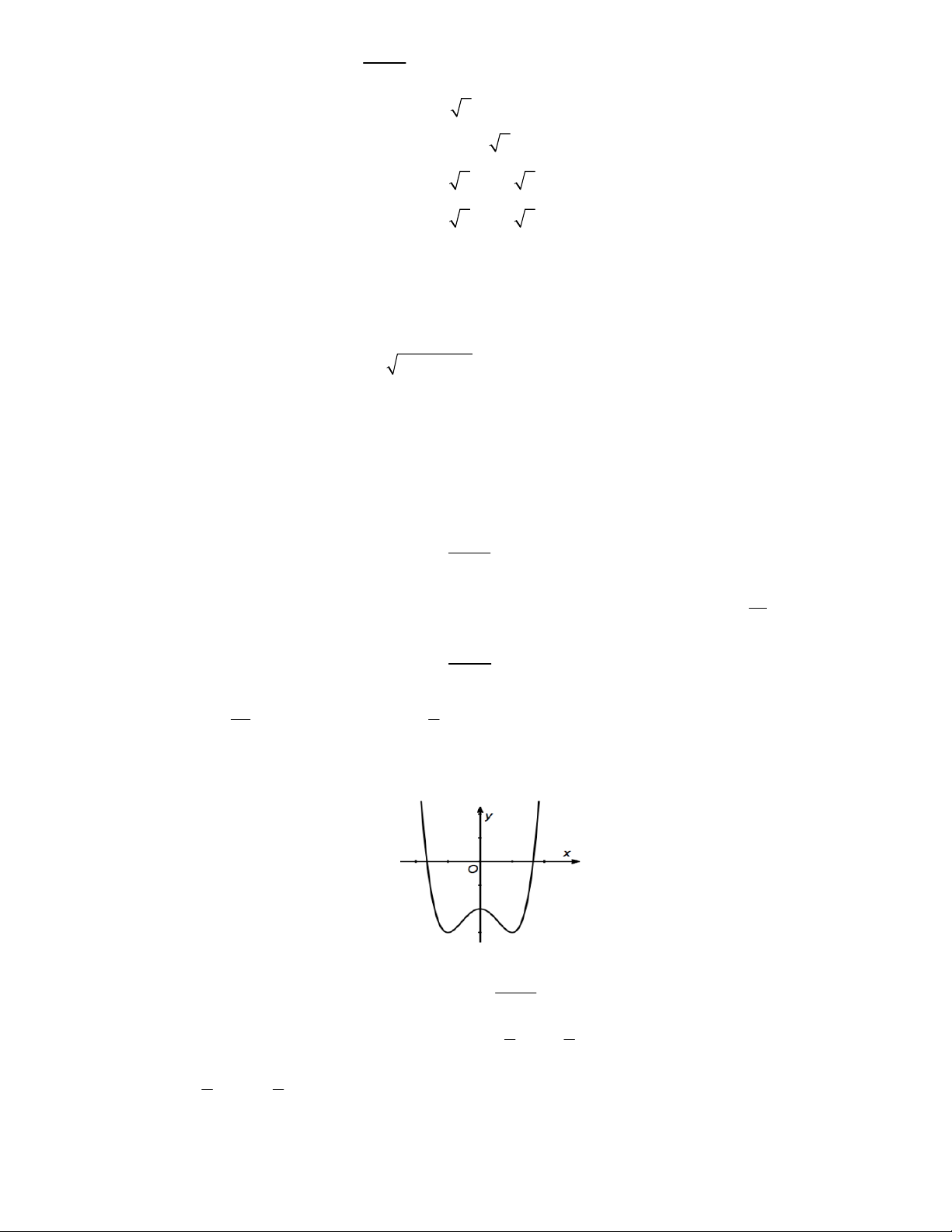
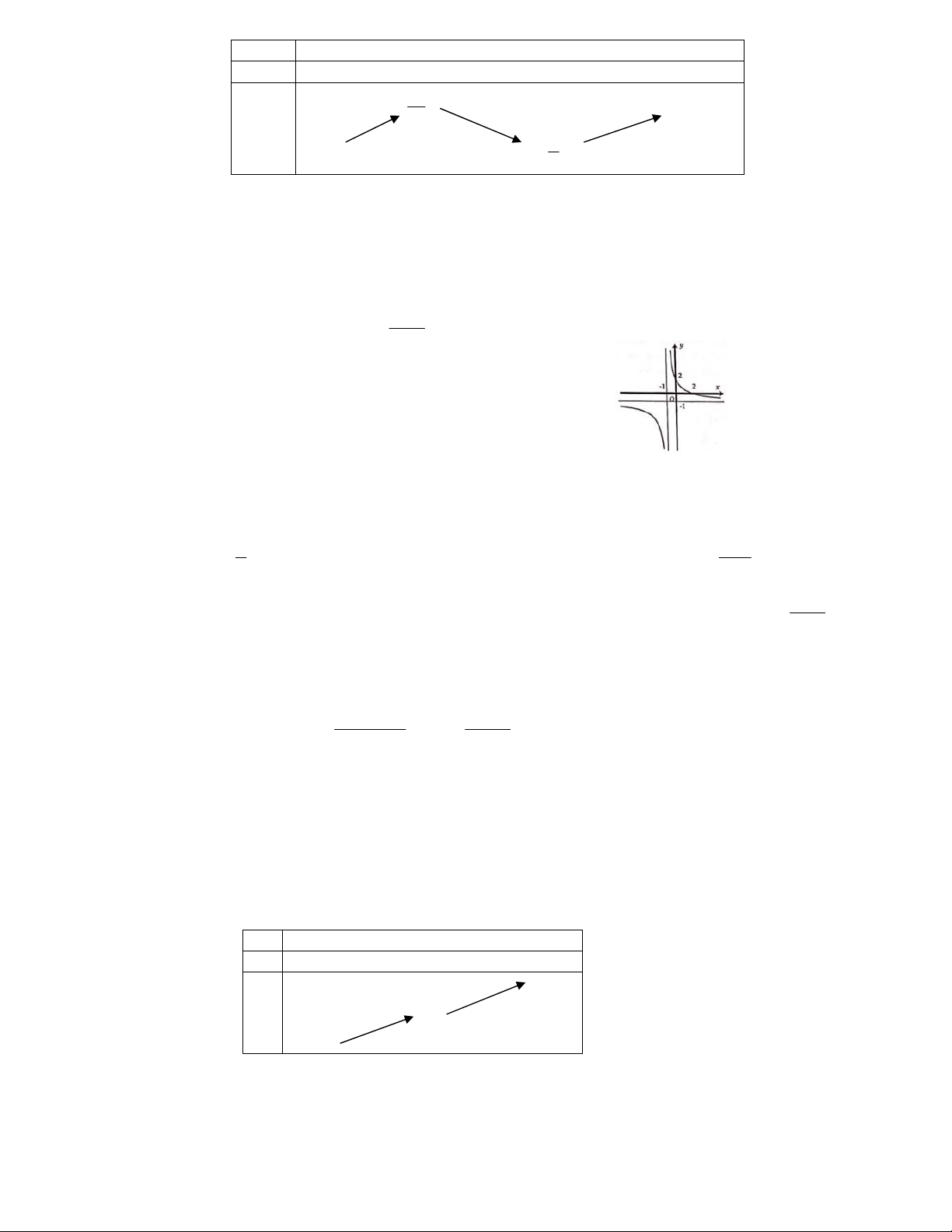
Câu 1. Đồ thị trong hình dưới là của hàm số nào. y 2 x 1 -1 O -2 A. 4 2 y = x - + 2x B. 3
y = -x + 3x . C. 3
y = x -3x . D. 4 2
y = x -2x . Câu 2. Cho hàm số 1 3 2
y = x -2x + 3x +1 có đồ thị là (C) . Tiếp tuyến của (C) song song với đường 3
thẳng D : y = 3x +1 có phương trình là:
A. y = 3x -1 . B. 26 y = 3x - .
C. y = 3x -2 . D. 29 y = 3x - . 3 3 Câu 3. Hàm số 3 2
y = -x + 3x + 9x + 4 đồng biến trên khoảng: A. (3;+¥) . B.(-3; ) 1 . C. ( ; -¥ -3). D. (-1;3).
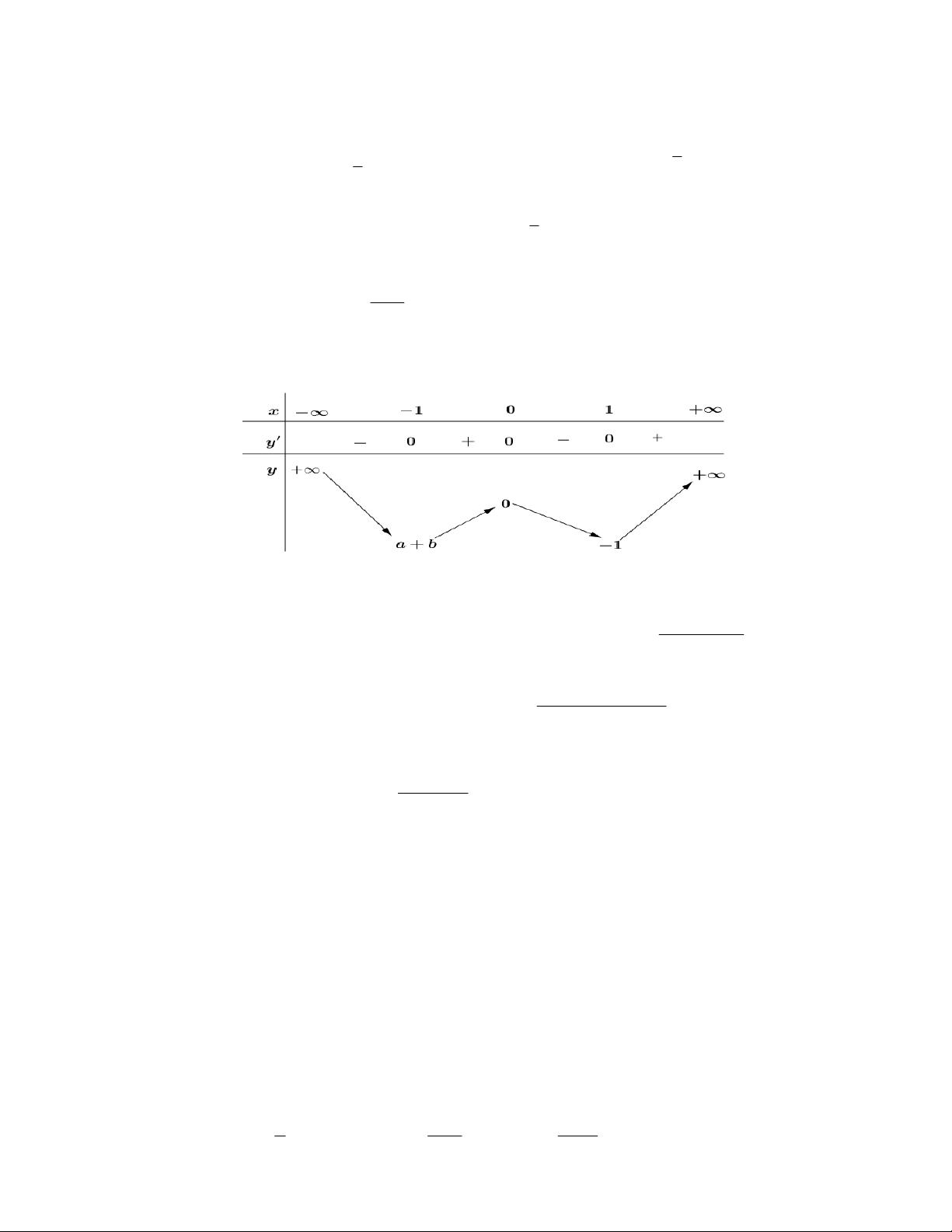
Câu 4. Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên: x 3 -¥ 1 +¥ y ' - 0 + 0 - +¥ y 1 1 - -¥ 3
Khẳng định nào sau đây là đúng ?
A. Hàm số có giá trị cực đại bằng 3 . B. Hàm số có GTLN bằng 1, GTNN bằng 1 - . 3
C. Hàm số có hai điểm cực trị. D. Đồ thị hàm số không cắt trục hoành. é ù
Câu 5. Giá trị nhỏ nhất của hàm số 1
y = x -5 + trên đoạn 1 ê ;5ú bằng: x ê2 ú ë û A. 5 - . B. 1 . C. -3 . D. -5 . 2 5 Câu 6. Hàm số 4 2
y = -x -3x +1 có:
A. Một cực đại và hai cực tiểu.
B. Một cực tiểu và hai cực đại.
C. Một cực đại duy nhất.
D. Một cực tiểu duy nhất.
Câu 7. Giá trị của x -
m để đường thẳng d : x + 3y + m = 0 cắt đồ thị hàm số 2 3 y = tại hai điểm M , x -1
N sao cho tam giác AMN vuông tại điểm A (1;0) là:
A. m = 6 .
B. m = 4 . C. m = 6 - .
D. m = -4 .
Câu 8. Với tất cả giá trị nào của m thì hàm số 4 y mx (m ) 1 x2 = + -
+1-2m chỉ có một cực trị: é £ A. m m ³1 .
B. m £ 0 .
C. 0 £ m £1. D. 0 ê . êm ³1 ë
Câu 9: Hàm số nào sau đây là hàm số nghịch biến trên  ? x  3 A. 3 2
y x  3x  2 B. 3 2 y  2
x x x  2 C. 4 2
y  x  2x  2 D. y x 1
Câu 10. Khẳng định nào sau đây là đúng về tính đơn điệu của hàm số 3 2
y x  3x 1?
A. Hàm số nghịch biến trên khoảng 0;2 B. Hàm số đồng biến trên khoảng 0; 2
C. Hàm số nghịch biến trên khoảng 0;  D. Hàm số đồng biến trên khoảng ; 2. Câu 11. Hàm số 4 2
y x  2x 1 đồng biến trên khoảng nào ?
A. (; 0) B. (0; ) C. (1; ) D. (1; 0)
Câu 12. Tìm giá trị của m để hàm số 3 2
y x  3mx  2m  
1 x  2 đạt cực trị tại x  1 A. m  1 B. m  1  C. m  2
D. Không tồn tại m
Câu 13. Có bao nhiêu giá trị của m để đồ thị hàm số 4 2
y x  2(m 1)x m có 3 điểm cực trị ,
A B,C sao cho BC  2 , trong đó A là điểm cực trị thuộc trục tung, B và C là 2 điểm cực trị còn lại
A. 0 B. 2 C. 1 D. 3 1  2
Câu 14. Đồ thị hàm số x y
có đường tiệm cận đứng và đường tiệm cận ngang là ? x  2 1 1 A. x  2,
y  2 B. x  2, y C. x  2, y  2
D. x  , y  2  . 2 2
Câu 15. Đồ thị hàm số 2
y x x 1  x có bao nhiêu đường tiệm cận ngang ? A. 0 B. 1 C. 2 D. 3
Câu 16. Cho đồ thị hàm số ( C) 3
y x  3x  3 . Khẳng định nào sau đây là sai ?
A. Đồ thị (C) nhận điểm I (0;3) làm tâm đối xứng.
B. Đồ thị (C) cắt trục hoành tại hai điểm phân biệt.
C. Đồ thị (C) tiếp xúc với đường thẳng y  5
D. Đồ thị (C) cắt trục tung tại một điểm.
Câu 17. Cho đồ thị hàm số ( C) 4 2
y x  2x  3. Khẳng định nào sau đây là sai ?
A. Đồ thị (C) nhận trục tung làm trục đối xứng
B. Đồ thị (C) cắt trục hoành tại hai điểm phân biệt.
C. Đồ thị (C) có 3 điểm cực trị tạo thành một tam giác vuông.
D. Đồ thị (C) tiếp xúc với đường thẳng y  2 
Câu 18. Bảng biến thiên sau của hàm số nào ? x -  0 2  y' - 0 + 0 - +  0 y -4 -  A. 3 2
y x  3x B. 3 2
y  x  3x C. 3 2
y x  3x  4 D. 3 2
y  x  3x  4  Câu 19. Gọi x
A, B là giao điểm của hai đồ thị C 2 1 : y
và đường thẳng d : y  2x . Khi đó độ x  1 dài đoạn AB là:
A. AB  4 B. AB  2 2
C. AB  10
D. AB  2 3 .
Câu 20.Số giao điểm của đồ thị hàm số 2
y  (x  3)(x x  4) với trục hoành là : A. 2 B. 3 C. 0 D. 1 x  2
Câu 21. Tiếp tuyến của đồ thị hàm số y
tại giao điểm với trục Ox có phương trình : x 1
A. y x  2 B. y  x  2
C. y x  2
D. y  x  2 Câu 22. Cho hàm số 3 2
y ax bx cx d a  0 có đồ thị như hình vẽ dưới đây. Khẳng định nào
sau đây về dấu của a, , b ,
c d là đúng nhất ? A. a d
, 0. B. a  0, c  0  .
b C. a, , b ,
c d  0. D. a d  , 0, c  0. 3x 1
Câu 23. Đồ thị hàm số y
có số đường tiệm cận là ? 2 x  7x  6
A. 1. B. 2. C. 3. D. 4. 2 x x  4
Câu 24. Kí hiệu m và M lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số y  trên x 1 M đoạn 0;3 
 . Tính giá trị của tỉ số . m 5 4 2 A. .
B. . C. 2. D. . 3 3 3 (m + ) 1 x + 2m + 2
Câu 25. Với các giá trị nào của tham số m thì hàm số y =
nghịch biến trên khoảng x + m ( 1; - +¥) ? ém <1
A. m <1 .
B. m > 2 . C. ê . D. . ê 1 £ m < 2 m > 2 ë
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN
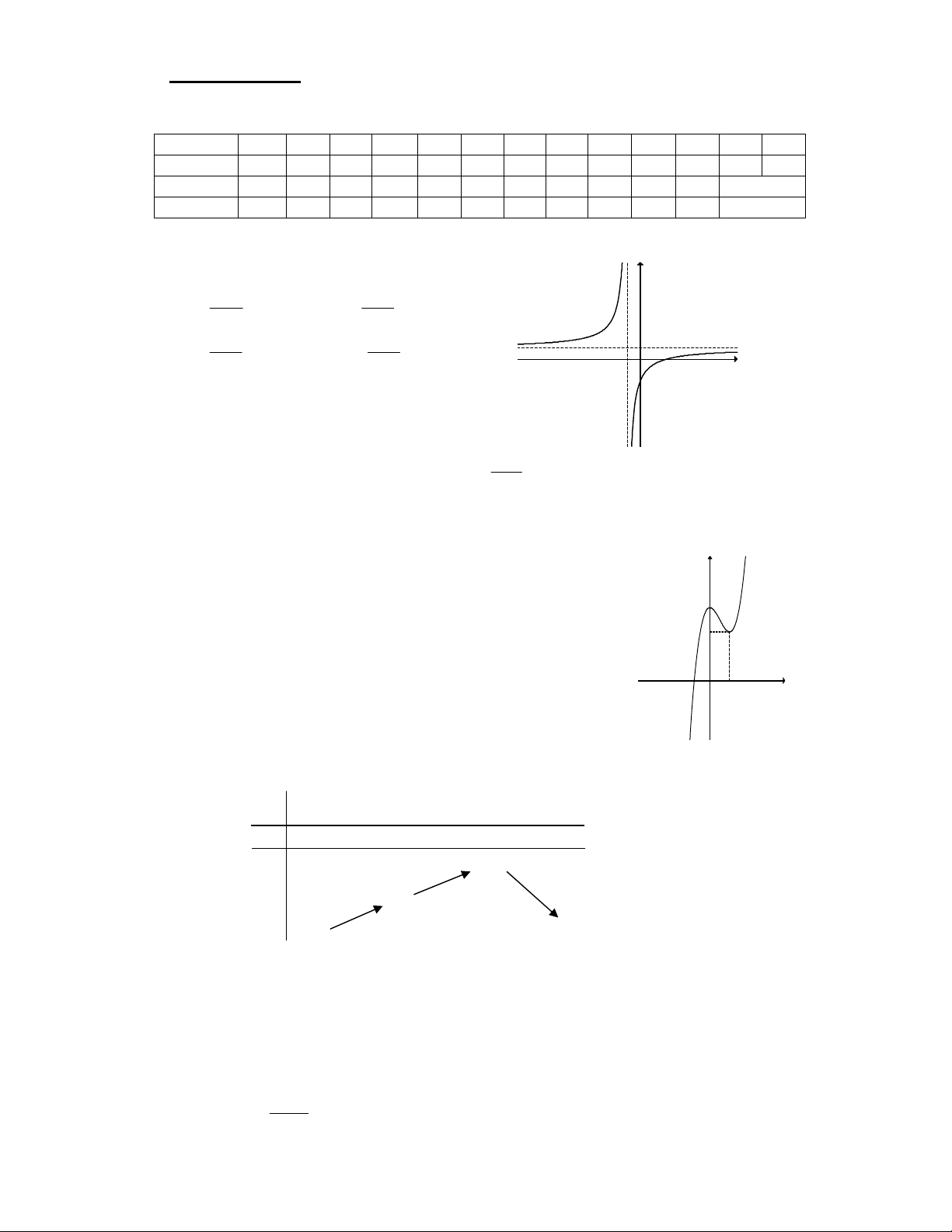
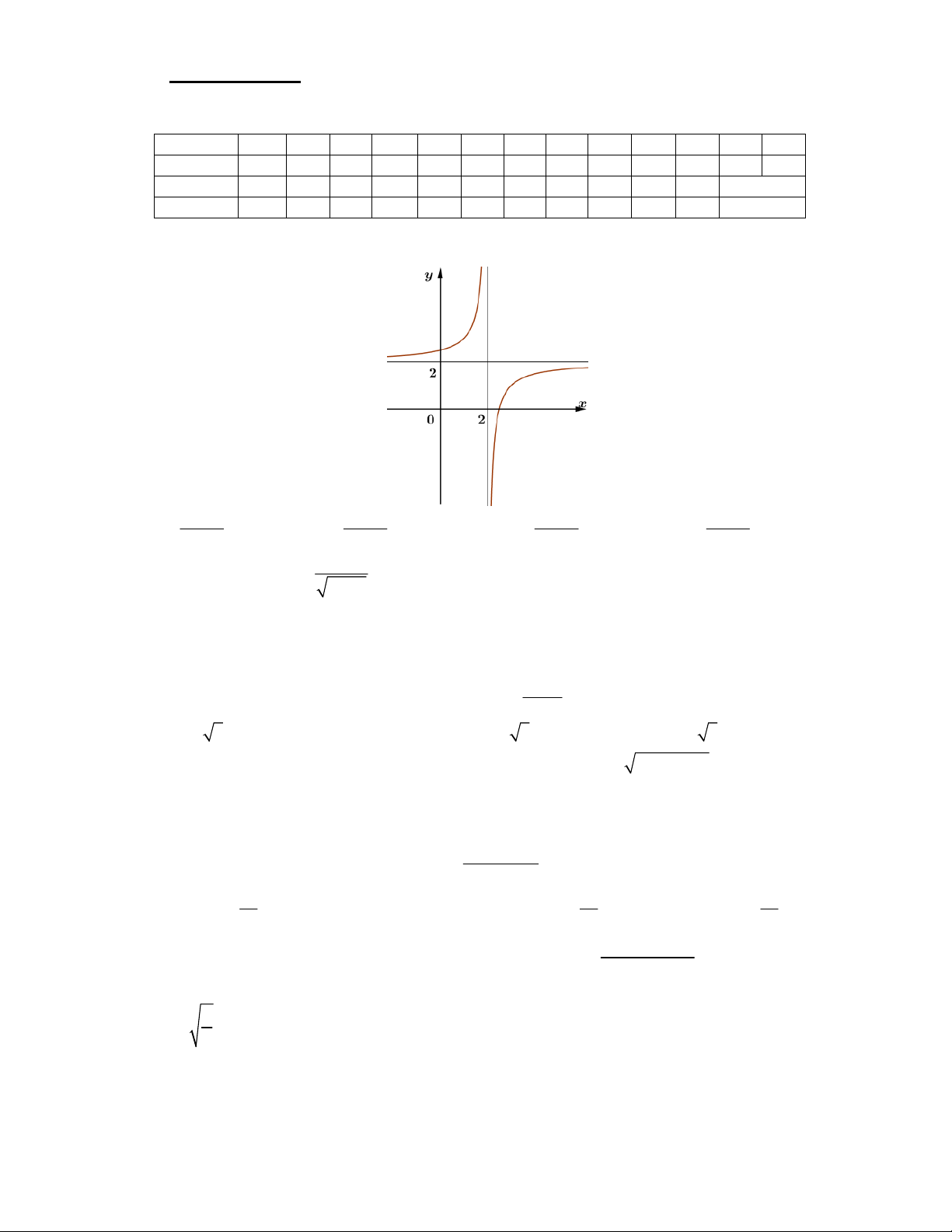
Câu 1. Đồ thị ở hình bên là đồ thị của hàm số nào
trong bốn hàm số dưới đây ? y A. x + 2 x - y = . B. 2 y = . x -1 x +1 C. 2 - x x - 1 y = . D. 2 y = . x +1 x -1 -1 O x
Câu 2. Hệ số góc của tiếp tuyến đồ thị hàm số x -1 y =
tại giao điểm của đồ thị hàm số với trục tung x +1 bằng: A. 2. B. 1. C. - 2 . D. -1 .
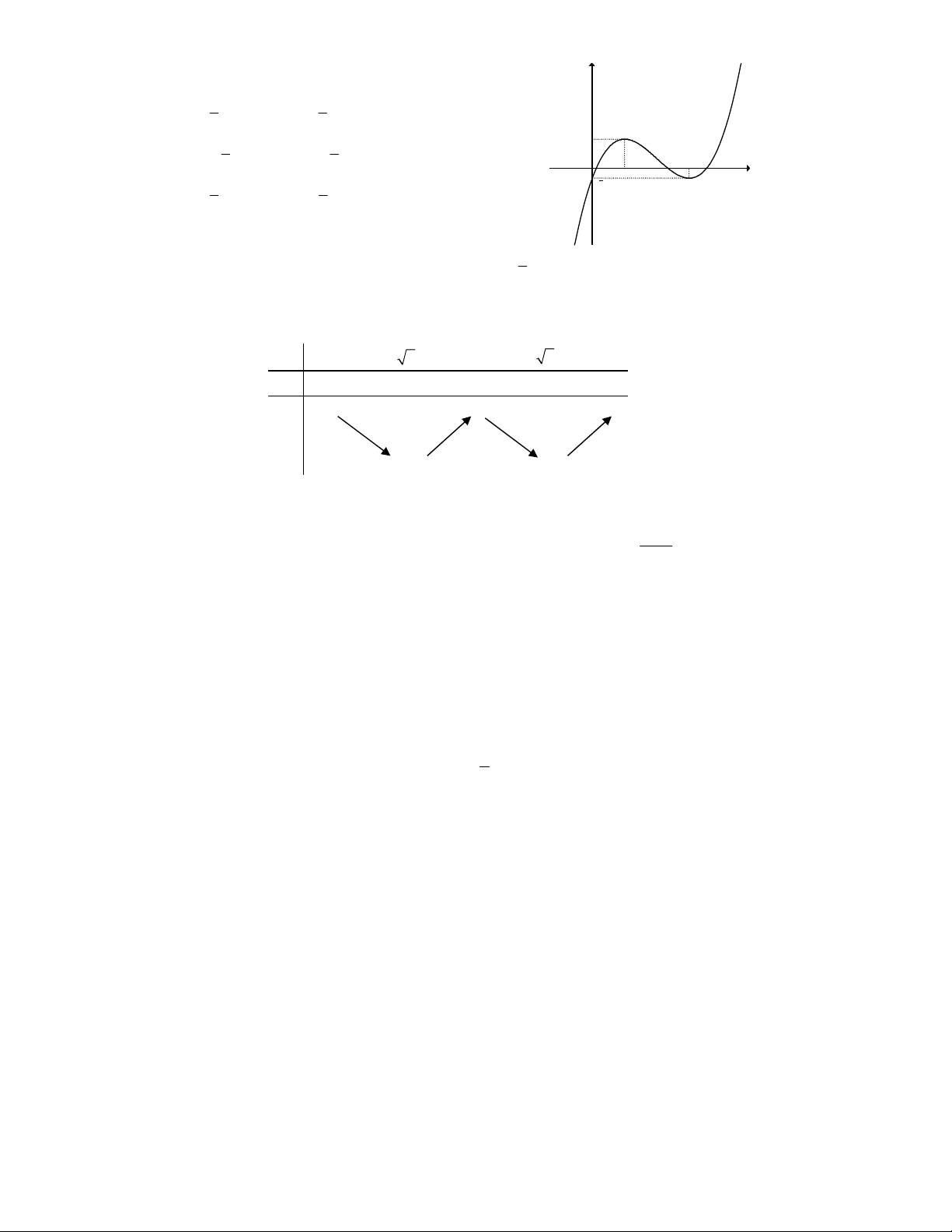
Câu 3. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y
Khẳng định nào sau đây là sai:
A. Hàm số đồng biến trên khoảng ( ;3 -¥ ) và (1;+¥) . 3 2
B. Hàm số đạt cực trị tại các điểm x = 0 và x =1 . x
C. Hàm số đồng biến trên khoảng ( ;0 -¥ ) và (1;+¥) . -1 O 1
D. Hàm số nghịch biến trên khoảng (0; ) 1 .
Câu 4. Cho hàm số y = f (x) liên tục trên  và có bảng biến thiên như hình dưới đây. Số mệnh đề sai
trong các mệnh đề sau đây? x -¥ -3 -2 +¥ y ' + 0 + 0 - 5 y 0 -¥ -¥
I. Hàm số đồng biến trên các khoảng ( ; -¥ -5) và (-3;-2) .
II. Hàm số đồng biến trên khoảng ( ;5 -¥ ) .
III. Hàm số nghịch biến trên khoảng (-2;+¥) .
IV. Hàm số đồng biến trên khoảng ( ; -¥ -2) .
A. 1. B. 2 .
C. 3 . D. 4 . Câu 5. Hàm số x -1 y =
đạt giá trị lớn nhất trên đoạn [0;2] tại: 2x +1 A. x = 0 . B. x = 2 . C. x = 3 . D. 1 x = - . 2
Câu 6. Đồ thị hàm số nào sau đây không có cực trị ? A. 3 2
y = x - x - x . B. 3 2
y = -x + x +1 . C. 3 2
y = -x + x - x . D. 3 2
y = x + x -1 . Câu 7. Tìm x +
m để đường thẳng d : y = x -m cắt đồ thị hàm số (C) 1 : y =
tại hai điểm phân biệt x -1
A, B sao cho AB = 3 2 .
A. m = 2 .
B. m = 4 .
C. m = 1 .
D. m = 3 . 2
Câu 8. Số đường tiệm cận của đồ thị hàm số 4 - x y = là: 2 x -3x - 4 A. 0 . B. 2 . C. 3 . D. 1.
Câu 9. Cho hàm số y f (x) liên tục trên  và phương trình f (x)  0 có ba nghiệm thực
phân biệt. Xét các hình dưới đây, những hình nào có thể là đồ thị của hàm số f (x) ? (1) (2) (3) (4)
A. 1 và 2. B. 1, 2 và 4. C. 1 và 3. D. 2 và 4.
Câu 10. Tìm tổng giá trị lớn nhất và nhỏ nhất của hàm số 4 2
f (x)  2x  4x 10 trên đoạn [0; 2] ? A. 12; 6  B. 12 C. 6 D. 6 2 x  4x  2
Câu 11. Tìm giá trị lớn nhất của hàm số f x  trên đoạn  1;  3. x  3 14 5 26
A. max f x  2. B. max f x 
. C. max f x  .
D. max f x  .  1;   3  1;   3 5  1;   3 2  1;   3 3
Câu 12. Tìm m sao cho hàm số y f x 3 2
x  3mx  m  
1 x  2 đạt cực đại tại x  2.
A. m  1.
B. m  3. C. m  1.  D. m .  x 1
Câu 13: Cho đồ thị hàm số (C): y 
, trong các kết luận sau, kết luận nào đúng: 2 x  x  2
A. Đồ thị hàm số (C) có một tiệm cận đứng là x  2 và một tiệm cận ngang là trục hoành.
B. Đồ thị hàm số (C) có hai tiệm cận đứng là x  2 và x  1 một tiệm cận ngang là trục hoành.
C. Đồ thị hàm số (C) có một tiệm cận ngang là trục tung và hai tiệm cận đứng là x  2 và x  1.
D. Đồ thị hàm số (C) có một tiệm cận ngang là trục tung và một tiệm cận đứng duy nhất là x=1. mx 1
Câu 14: Với giá trị nào của m thì hàm số y 
tăng trên từng khoảng xác định ? x 1 A. m  0 B. m  1 C. m  1 D. m  0
Câu 15: Gọi M và m lần lượt là GTLN và GTNN của hàm số 2
y  x 1 x trên tập xác định. Khi đó M – m bằng: A. 1 B. 2 C. 3 D. đáp số khác
Câu 16. Đồ thị ở hình bên là đồ thị của hàm số
nào trong bốn hàm số dưới đây? y A. y  4 x  2 B. y  3 x  2 3x  2 . C. y = 4 x - 2 2x + 2 . D. y   4 x  2 2x  2 . x O 2x 1 Câu 17. Cho hàm số + y =
có đồ thị là (C). Phương trình tiếp tuyến của (C) có hệ số góc bằng x -2 5 là:
A. y = -5x + 2 và y = -5x + 22 .
B. y = 5 x + 2 và y = -5x + 22 .
C. y = -5x + 2 và y = -5x - 22 .
D. y = -5x - 2 và y = -5x + 22 . Câu 18. Hàm số 4 2
y = -x - x - 2 nghịch biến trên khoảng: A. (0;+¥) . B. ( ;0 -¥ ). C. (-1;+¥) . D. ( ) ;1 -¥ .
Câu 19. Giá trị lớn nhất của hàm số y = 5- 4x trên đoạn [-1; ] 1 bằng: A. 9. B. 3. C. 1. D. 0. x + 3
Câu 20. Tìm tất cả giá trị của m để phương trình
-m = 0 có nghiệm âm: x -2 3 3 3 3
A. m ³ - . B.- < m <1 . C.- £ m £1 . D. m > - . 2 2 2 2
Câu 21. Tìm m để hàm số 3 2
y = -x + 3x + m -1 có giá trị cực đại là y
, giá trị cực tiểu là y thỏa max min mãn y .y = 5 : max min
A. m = -4 hoặc m = -2 .
B. m = 4 hoặc m = 2 .
C. m = -4 hoặc m = 2 .
D. m = 4 hoặc m = -2 .
Câu 22. Cho hàm số y f (x) có bảng biến thiên sau:
Khẳng định nào dưới đây là khẳng định sai ?
A. Đồ thị hàm số có một tiệm cận ngang y  2. B. Hàm số đạt cực đại và cực tiểu.
C. min f (x)  y và max f (x)  y . D. Hàm số đồng biến trên khoảng  2;  . CT CÑ 2 2x x 1
Câu 23. Tìm giá trị cực tiểu y của hàm số y  . CT x 1
A. y  0. B. y  7.
C. y  1. D. y  8.  CT CT CT CT
Câu 24. Tìm giá trị nhỏ nhất của hàm số 3 2
y  2x  9x 1 trên đoạn  4;    1 . A. miny  1.
B. miny  8. C. miny  28. D. miny  5.  4;    1  4;    1  4;    1  4;    1
Câu 25. Đồ thị của hàm số nào dưới đây có tiệm cận đứng ? 2 x 1 2 x x 1 A. 2
y x  2x  3. B. y  . C. y  . D. 3
y x  2x 1. 2 x x 1 2 x 1
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN
Câu 1. Đồ thị hình bên là đồ thị của hàm số nào sau đây? y A. 3 2
y = x -3x +1 . 2 B. 4 2
y = -x + 2x -2 . x -1 O 1 C. 4 2
y = -x + 2x +1 . D. 4 2
y = x -2x +1 . 2 x +1
Câu 2. Đồ thị hàm số y =
có bao nhiêu đường tiệm cận ? 4 2 x + 3x + 2 A. 0. B. 1. C. 2. D. 3. 2x -1
Câu 3. Hàm số y =
nghịch biến trên khoảng nào ? x -3 A. ( ; -¥ +¥) . B. ( ;4 -¥ ) . C. (0; ) +¥ . D. (3;4) . 4
Câu 4. Giá trị lớn nhất của hàm số y = là: 2 x + 2 A. 3. B. 2. C. -5 . D. 10.
Câu 5. Tìm tất cả các giá trị của m để PT 4 2
x - 2x +1+ m = 0 có bốn nghiệm phân biệt. A. m < -1. .
B. -1 < m <1 . C. m >1 .
D. -1 < m < 0 1
Câu 6. Tìm m để hàm số 3 2
y = x + mx +( 2
m - 4)x + 2 đạt cực tiểu tại x = 1. 3 A. m = -2 . B. m = -1. C. m = 1 .
D. Không có m . x -2016
Câu 7. Đồ thị (C) của hàm số y =
cắt trục tung tại điểm M có tọa độ ? 2x +1 A. M (0;0). B. M (0; 201 - 6). C. M (2016;0) . D. (2016; 2016 - ) . ax b
Câu 8. Cho hàm số y
có đồ thị C. Đồ thị C nhận đường thẳng y  3 làm tiệm cận x  2
ngang và C đi qua điểm A3; 
1 . Tính giá trị của biểu thức P a  . b
A. P  3. B. P  5.  C. P  8.
D. P  5.
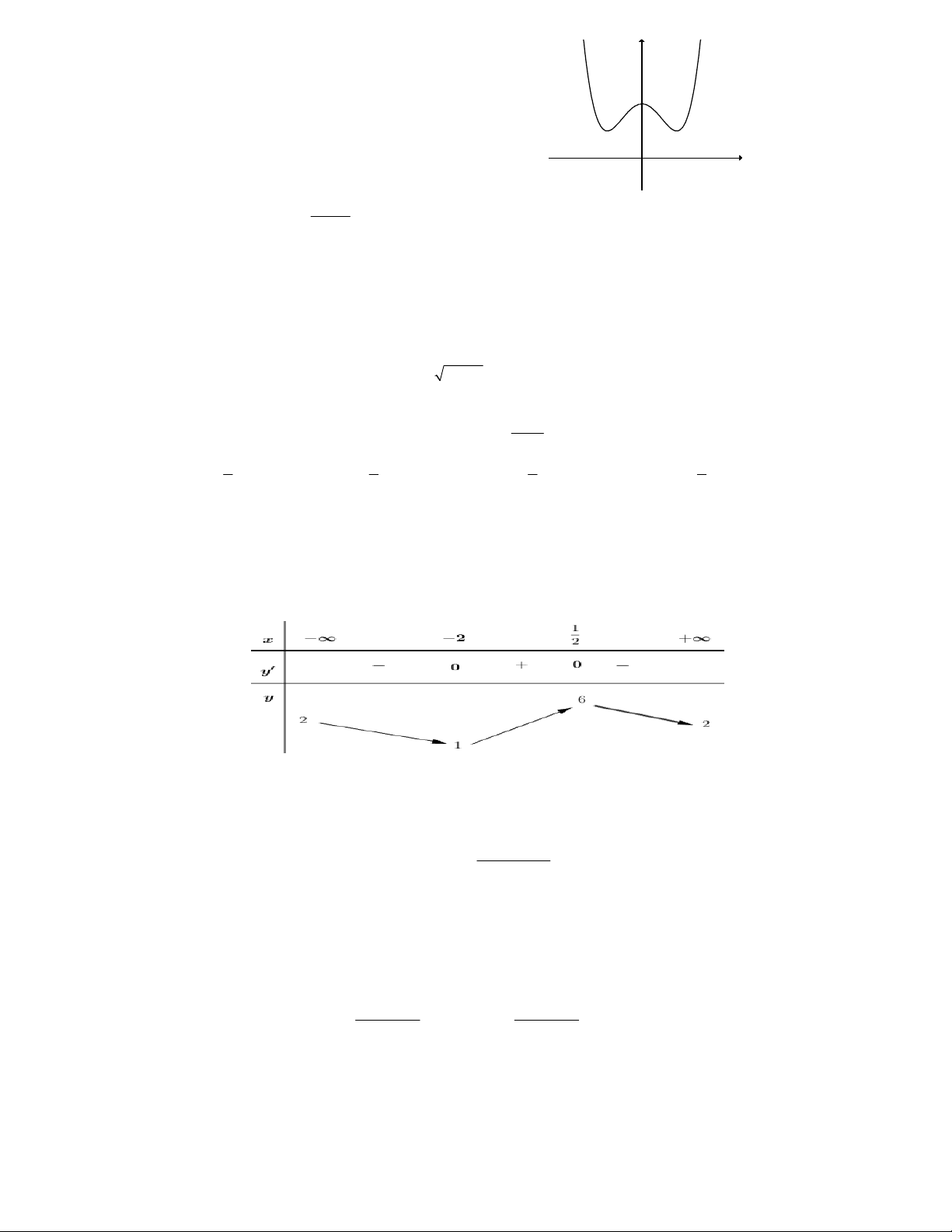
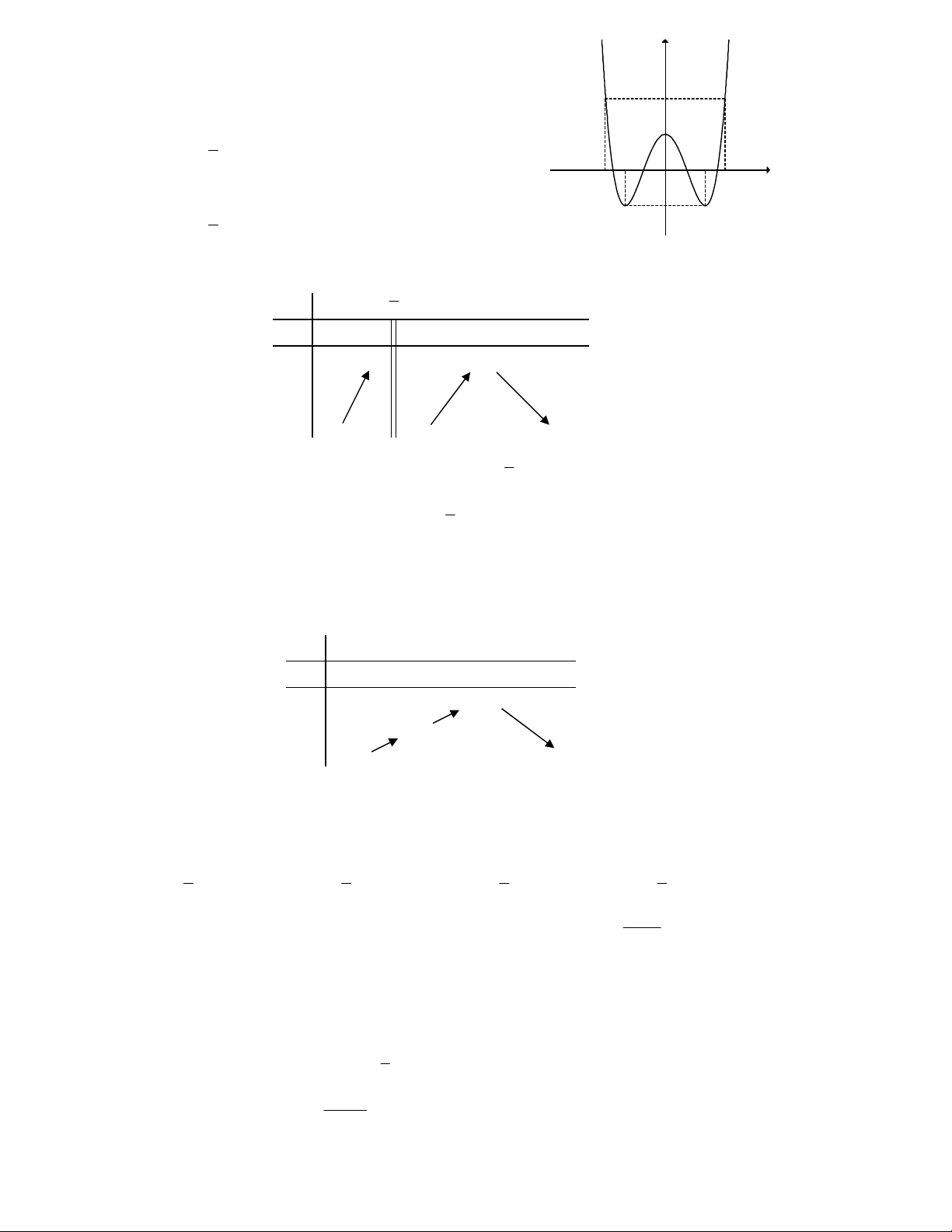
Câu 9. Cho đồ thị của hàm số 4 2
y ax bx c (a  0) như hình vẽ. Khẳng định nào sau đây là khẳng định đúng ?
A. a  0, b  0, c  0. B. a  0, b  0, c  0. C. a  0, b  0, c  0. D. a  0, b  0, c  0. x +1
Câu 10. Cho hàm số y =
. Chọn phương án đúng trong các phương án dưới đây ? 2x -1 1 11 1 A. min y = . B. max y = 0 . C. min y = . D. max y = . [ 1; - 2] 2 [-1;0] [3;5] 4 [-1; ] 1 2
Câu 11. Trong các hàm số sau, hàm số nào vừa có khoảng đồng biến vừa có khoảng nghịch
biến trên tập xác định của nó. x + (I) 2 1 . y = . (II) 4 2
. y = -x + x -2. (III) 3
. y = x + 3x - 4. x +1 A. (I) . B. (II) . C. (II); (III) . D. (I); (III) .
Câu 12. Tìm điểm cực tiểu của đồ thị hàm số 3 2 y = x - + 3x + 4 . A. ( 0; 2). B. M (0;4) . C. M (2;0). D. (0; 4). x +
Câu 13. Cho hàm số y = f (x) 3 1 =
. Khẳng định nào dưới đây là khẳng định đúng ? 1-2x
A. Đồ thị hàm số y = f (x) có tiệm cận ngang là y = 3 .
B. Đồ thị hàm số y = f (x) có tiệm cận đứng là x = 1 . 3
C. Đồ thị hàm số y = f (x) có tiệm cận ngang là y = - . 2
D. Đồ thị hàm số y = f (x) không có tiệm cận.
Câu 14. Đồ thị hàm số 3 2
y = x -3x -2x cắt trục hoành tại bao nhiêu điểm ? A. 4 . B. 3 . C. 2 . D. 1.
Câu 15. Đường thẳng y = m cắt đồ thị hàm số 3
y = x -3x + 2 tại ba điểm phân biệt khi:
A. 0 £ m < 4 . B. m > 4 .
C. 0 < m £ 4 .
D. 0 < m < 4 . Câu 16. Cho hàm số 3 2
y = -x + 3x +1 , có đồ thị là (C). Viết phương trình tiếp tuyến của đồ thị
hàm số (C) tại điểm A (3; ) 1 .
A. y = 20 -9x .
B. 9x + y -28 = 0 .
C. y = 9x + 20 .
D. 9x - y + 28 = 0 . m Câu 17. Hàm số 3 2 y =
x + x + x + 2017 có cực trị khi và chỉ khi: 3 m ìï <1 m ìï £1
A. m £1 . B. ïí . C. ïí . D. m <1 . m ï ¹ 0 ïî m ï ¹ 0 ïî
Câu 18. Hàm số f x 4 2
x  4x có số điểm cực trị là ?
A. 1. B. 3. C. 2. D. 4.
Câu 19. Tìm giá trị lớn nhất và nhỏ nhất của hàm số f x 3 2
x  3x  9x 10 trên  4;  2.
A. max f x  37; min f x  5. B. max f x  40; min f x 12.  4;  2  4;  2  4;  2  4;  2
C. max f x  30; min f x  4. D. max f x  50; min f x  6.  4;  2  4;  2  4;  2  4;  2 2 x  3x  9
Câu 20. Cho M là điểm có tọa độ nguyên, thuộc đồ thị hàm số y  . Hỏi có bao nhiêu x  2
điểm M thỏa mãn bài toán ? A. 5.
B. 4. C. 6. D. 7.
Câu 21. Cho hàm số C 3
: y  x  3x và d : y mx  
1  2 . Tìm tất cả giá trị thực của tham số m
sao cho d cắt C tại ba điểm phân biệt. 9 9 9
A. m   và m  0.
B. m   . C. m  0. D. m   và m  3.  4 4 4
Câu 22. Hàm số nào sau đây đồng biến trên  . x -1 1 1 A. y = . B. y = 3 x - 2 x - x . C. y = 4 x - 4x - 2 . D. y = 3 x + 2 3x + 3x -1 . x + 2 3 2
Câu 23. Hàm số bậc ba = 3 + 2 y ax
bx + cx + d có thể có bao nhiêu cực trị ? A. 1, 2 hoặc 3 . B. 0 hoặc 2 . C. 0, 1 hoặc 2 . D. 2 .
Câu 24. Gọi A, B, C lần lượt là ba điểm cực trị của đồ thì hàm số y = 4 x - 2 2 4x +1 . Tính diện
tích của tam giác ABC . A. 4 . B. 2 . C. 1. D. 2 . ax +1
Câu 25. Biết rằng đồ thị hàm số y =
có tiệm cận đứng là x = 2 và tiệm cận ngang là bx - 2
y = 3 . Tính giá trị của biểu thức P = a + b . A. P = 1 . B. P = 4 . C. P = 0 . D. P = 5 .
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN
Câu 1. Đường cong trong hình dưới đây là đồ thị của hàm số nào ? 2x  5 2x  5 2x  5 2x  5 A. y  . B. y  . C. y  . D. y  . x  2 x  2 x  2 x  2 x  2
Câu 2. Đồ thị hàm số y
có bao nhiêu đường tiệm cận ? 2 x 1
A. 1. B. 2. C. 3. D. 0.
Câu 3. Tìm điều kiện của a, ,
b c để hàm số 3 2
y ax bx cx d (a  0) đồng biến trên .  A. 2
a  0, b  3ac  0. B. 2
a  0, b  3ac  0. C. 2
a  0, b  3ac  0. D. 2
a  0, b  3ac  0. 2x
Câu 4. Tìm giá trị cực tiểu y của hàm số y  2x 1 . CT 2 x 1
A. y  3 3 1. B. y  1.
C. y  3 3. D. y 1 3 3. CT CT CT CT
Câu 5. Biết đường thẳng d : y  2x 1 cắt đồ thị C của hàm số 2
y x  3x  5 tại điểm duy nhất,
kí hiệu  x ; y là tọa độ của điểm đó. Tìm y . 0 0  0
A. y  2.
B. y  3. C. y  1.
D. y  4. 0 0 0 0 2 x  2x  3
Câu 6. Tìm giá trị lớn nhất của hàm số f x  trên đoạn 0;  3 . x  2 12 17 14
A. max f x 
. B. max f x  12. C. max f x 
. D. max f x  . 0; 3 5 0; 3 0; 3 5 0; 3 5 2 x 1
Câu 7. Tìm tất cả các giá trị thực của a sao cho đồ thị hàm số y  có đúng một tiệm 2
3x  2xa a cận đứng. 3 A. a   .
B. a  0 hoặc a  3. C. a  1 hoặc a  2. D a  2.  2
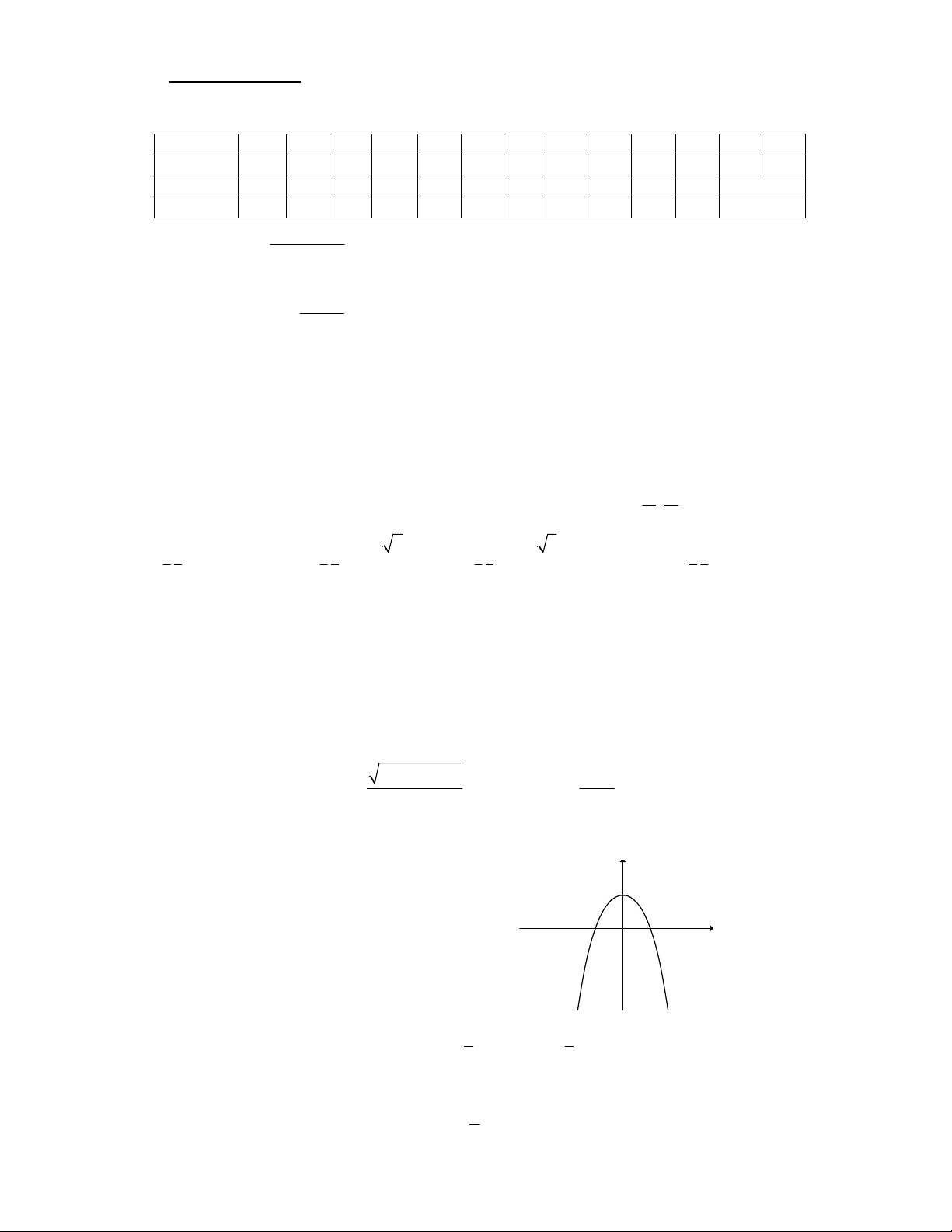
Câu 8. Hãy xác định hệ số , a ,
b c để hàm số y 4 2
y = ax + bx + c có đồ thị như hình vẽ. 4
A. a = -4, b = -2, c = 2 . 2 1
B. a = , b = 2 - , c = 2 . 4 x -2 2 -3 O 3
C. a = 4, b = 2, c = -2 . 1 -2
D. a = , b = 2, c = 2 . 4
Câu 9. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào đúng trong các mệnh đề dưới đây. 1 - x -¥ 2 3 +¥ y ' + + 0 - +¥ 4 y -¥ -¥ -¥ æ 1ö
A. Hàm số đồng biến trên các khoảng çç ; ÷ -¥ - ÷ ç và (3;+¥) . è 2÷ø æ 1 ö
B. Hàm số đồng biến trên khoảng ç- ç ; ÷ +¥÷ ç . è 2 ÷ø
C. Hàm số nghịch biến trên khoảng (3;+¥) .
D. Hàm số đồng biến trên khoảng ( ;3 -¥ ) .
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Khẳng định nào dưới đây là khẳng định sai? x -¥ 0 3 +¥ y ' + 0 + 0 - 27 y 0 -¥ -¥
A. Điểm cực đại hàm số là x = 3 .
B. Giá trị cực đại của hàm số là 27 .
C. Giá trị lớn nhất của hàm số là 27 .
D. x = 0 là một điểm cực trị của hàm số. Câu 11. Cho hàm số 4 2
y = cos x + sin x . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng ? 1 3 5 7 A. . B. . C. . D. . 4 4 4 4 2x -1
Câu 12. Biết rằng đường thẳng y = x -1 cắt đồ thị hàm số y =
tại hai điểm phân biệt x +1
A (x ; y , B(x ; y và x > x . Khi đó, tính giá trị của biểu thức 2
P = y -2 y . B B ) A A ) A B A B A. P = 4 - . B. P = 1 - . C. P = 4 . D. P = 3 . Câu 13. Cho hàm số 3
y = x -2x . Hệ thức liên hệ giữa giá trị cực đại y và giá trị cực tiểu y là: CD CT 3
A. y = 2 y .
B. y = y .
C. y = y .
D. y + y = 0 . CT CD CT 2 CD CT CD CT CD 3x  9
Câu 14. Đồ thị hàm số y
có mấy đường tiệm cận ? 2 x  4
A. 1. B. 2. C. 4. D. 3. x  3
Câu 15. Tìm giá trị cực đại y của hàm số y  . CÑ 2 x 1 A. 3.
B. 7. C. 10. D. 5.
Câu 16. Hàm số nào sau đây có bảng biến thiên như hình bên dưới: x -¥ 2 +¥ y ' - - 3 +¥ y -¥ 3 3x -9 3x -7 3x -1 3x -8 A. y = . B. y = . C. y = D. y = . x -2 x -2 x -2 x -2 x -1
Câu 17. Đường thẳng y = x +8 là tiếp tuyến tại điểm nào của đồ thị hàm số y = ? x + 3 A. (3;-5) . B. ( 1; - - ) 1 . C. (1; ) 1 - . D. ( 5; - 3) .
Câu 18. Khẳng định nào sau đây đúng về hàm số 3 2
y = x -2x + x ? æ 1ö
A. Hàm số chỉ đồng biến trên khoảng çç ; ÷ -¥ ÷ ç . è 3÷ø
B. Hàm số chỉ đồng biến trên khoảng (1;+¥) . æ1 ö
C. Hàm số đồng biến trên khoảng çç ;1÷÷ ç . è3 ÷ø æ 1ö
D. Hàm số đồng biến trên các khoảng çç ; ÷ -¥ ÷ ç và (1;+¥) . è 3÷ø 2
7 + 3 cos x -sin x
Câu 19. Tìm giá trị nhỏ nhất của hàm số y = . 2 + cos x 10 5 A. 4. B. . C. 3. D. . 3 3
Câu 20. Đồ thị hàm số 3 2
y = x -3x + ax + b có điểm cực tiểu A (2;-2) . Tính a +b : A. 1. B. 2 . C. 3 . D. 4 .
Câu 21. Với giá trị nào của m thì phương trình 4 2
-x + 2x + m + 3 = 0 có 2 nghiệm phân biệt: A. m = 3 - . B. m Î( 3; - +¥)È{ 4
- } . C. m Î(- ; ¥ -3) . D. m = 4 - .
Câu 22. Đồ thị hàm số 4 2
y = ax + bx + c với ,
a b > 0 có mấy điểm cực trị ? A. 0 . B. 1. C. 2 . D. 3 . Câu 23. Cho hàm số 3 2 2
y = x -3mx + 4m - 2 . Tìm m để đồ thị hàm số có hai điểm cực trị A, B
sao cho I (1;0) là trung điểm của AB : A. m = 2 . B. m = 1 - . C. m = 1 . D. m = 0
Câu 24. Điều kiện của , a ,
b c để hàm số 3
y = ax + bx + c luôn nghịch biến trên  là:
A. ab > 0, "c Î  .
B. a < 0,b £ 0, "c Î  . C. ab < 0, "c Î  . D. a > 0,b ³ 0, "c Î  . 2 x  3x  3
Câu 25. Hàm số y
nghịch biến trên khoảng nào ? x  2 A. x  2.  B. ( ;  3
 ). C. (1;). D. ( 3  ; 2  ).
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN 2 x  3x  3
Câu 1. Hàm số y
nghịch biến trên khoảng nào ? x  2 A. (1;). B. ( ;  3  ). C. ( 3  ; 2  ).
D. x  2. ax b
Câu 2. Cho hàm số y
c  0, ad bc  0. Khẳng định nào dưới đây là sai ? cx d
A. Đồ thị luôn có một tiệm cận đứng.
B. Trong mọi trường hợp, trục tung không thể là tiệm cận đứng của đồ thị hàm số.
C. Đồ thị hàm số luôn có một tâm đối xứng.
D. Đồ thị luôn có một tiệm cận ngang.
Câu 3. Hàm số y  3 x  2
3x  3x  4 có bao nhiêu cực trị ? A. 2. B. 1. C. 0. D. 3.    
Câu 4. Tìm giá trị nhỏ nhất của hàm số y  5cos x  cos5x trên đoạn  ; .  4 4   
A. min y  4.
B. min y  3 2. C. min y  3 3.
D. min y  4.                  ;   ;  ;  ; 4 4     4 4     4 4     4 4   
Câu 5. Biết rằng đồ thị hàm số 2
y  x  8x  3 cắt đồ thị hàm số 3 2
y  2x  3x  9x  4 tại điểm duy
nhất M . Khẳng định nào dưới đây là khẳng định đúng ?
A. Điểm M thuộc góc phần tư thứ hai. B. Điểm M thuộc góc phần tư thứ nhất.
C. Điểm M thuộc góc phần tư thứ ba. D. Điểm M thuộc góc phần tư thứ tư.
Câu 6. Tìm m sao cho đồ thị hàm số 3 2
f (x)  2x  3(m 1)x  6m(1 2m)x có điểm cực đại và cực
tiểu nằm trên đường thẳng y  4 . x
A. m  1.
B. m  2. C. m  1.
D. m  2.
Câu 7. Tìm khoảng cách d giữa hai tiệm cận đứng của hai đồ thị hàm số sau: 3 3 2 8x x  2 x 1 f (x) 
C và g(x)  C '. x  3 x  2
A. d  4.
B. d  2. C. d  3.
D. d  1.
Câu 8. Đồ thị ở hình bên là đồ thị của
hàm số nào trong bốn hàm số dưới đây ? y A. 4 2
y = x -2x +1 . x B. 4 2
y = -x + 2x -1 . O C. 4 2
y = -x -2x +1 . D. 4 2
y = x + 2x -1 . 1 5
Câu 9. Khoảng nghịch biến của hàm số 3 2
y = x - x -3x + là: 3 3 A. ( ; -¥ - ) 1 . B.( 1; - 3). C. (3;+¥) . D. ( ; -¥ - ) 1 và (3;+¥). 2
Câu 10. Giá trị nhỏ nhất của hàm số 2
y = x + với x > 0 bằng: x A. 4. B. 3. C. 1. D. 2.
Câu 11. Cho hàm số y = (x - )( 2
1 x + mx + m). Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt. é 1 1 ê- ¹ m < 0 A. m > 4.
B. - ¹ m < 0.
C. 0 < m < 4. D. ê 2 . 2 ê êm > 4 ë 2 Câu 12. Hàm số 3 2
y = ax - ax +1 có điểm cực tiểu x = khi điều kiện của a : 3 A. a = 2 . B. a > 0 . C. a = 0 . D. a < 0 . x -
Câu 13. Cho đường cong (C) 2 : y =
. Điểm nào dưới đây là giao của hai tiệm cận của (C)? x + 2 A. L (-2;2) . B. M (2; ) 1 . C. N (-2;-2) . D. K (-2; ) 1 .
Câu 14. Cho bảng biến thiên sau:
Biết đây là bảng biến thiên của hàm số 4 2
y ax bx . Tìm giá trị của a và . b
A. a  1 và b  2.
B. a  2 và b  3.  C. a  1
và b  2. D. a  1
và b  2.  2 x  2mx 1
Câu 15. Với bài toán tìm tất cả các giá trị thực của m sao cho hàm số y  đạt cực đại x  2m
tại x  1, một học sinh đã tiến hành giải như sau: 2 2
x  4mx  4m 1
Bước 1. Tập xác định D   \ 2  
m và tính y '  . x  2m2
Bước 2. Hàm số đạt cực đại tại x  1  y '  1  0. 4m(1 m) m  0
Bước 3. Biến đổi y '  1  0   0    1 2m2 m 1
Kết luận m  0, m  1 thỏa mãn bài toán.
Học sinh giải đúng hay sai, nếu sai thì sai ở bước nào ?
A. Học sinh giải sai và sai ở bước 1.
B. Học sinh giải sai và sai ở bước 3.
C. Học sinh giải sai và sai ở bước 2.
D. Học sinh giải đúng.
Câu 16. Tìm giá trị lớn nhất, nhỏ nhất của hàm số f x 3 2
x  3x  9x  35 trên đoạn  4;  4.
A. max f x  15; min f x  41. B. max f x  8; min f x  41. 4;4 4;4  4;  4  4;  4
C. max f x  40; min f x  41. D. max f x  40; min f x  8.  4;4   4;4  4;  4  4;  4
Câu 17. Biết rằng đồ thị hàm số 3
y x  3x 1 cắt đồ thị hàm số 2
y  3x tại điểm duy nhất, kí hiệu
x ; y là tọa độ điểm đó. Tìm y . 0 0  0
A. y  3.
B. y  4. C. y  2.
D. y  5. 0 0 0 0
Câu 18. Trong các hàm số dưới đây, hàm số nào có tiệm cận đứng ? 2 x 1
A. f x 2017  x
x  . B. f x 1  3  x
. C. f x 
. D. f x 4 2
x x  2017. 3 x  3 2 x 1
Câu 19. Đồ thị ở hình bên là đồ thị của hàm số nào y
trong bốn hàm số dưới đây? 1 1 A. 3 2
y = x -2x + 3x - . 3 3 1 1 1 B. 3 2
y = - x + 2x -3x - . x 3 3 3 O 1 1 1 1 - 3 C. 3 2
y = x -3x + 4x - . 3 3 D. 3 2
y = x -6x + 9x -1 . 1
Câu 20. Tìm tất cả giá trị của số thực m để hàm số 3 2
y = x -mx +(2m - )
1 x -m + 2 đồng biến trên  . 3 A. m >1 . B. m = 1 . C. m ¹ 1 . D. m <1 . Câu 21. Cho hàm số 4 2
y = ax -bx +1 xác định và liên tục trên  và có bảng biến thiên: x -¥ - 2 0 2 +¥ y ' - 0 + 0 - 0 + +¥ a +¥ y 1-b 1-b
Giá trị của a và b thỏa đề bài là:
A. a = 1 và b = 2 .
B. a = -1 và b = -4 .
C. a = 1 và b = 4 . D. a = -1 và b = -2 . x -3
Câu 22. Số điểm có tọa độ là các số nguyên trên đồ thị hàm số y = là: x -2 A. 6 . B. 2 . C. 4 . D. 8 . Câu 23. Cho hàm số 4 2
y = x -2mx + 3m -1 . Khẳng định nào sau đây sai?
A. Hàm số có 1 cực trị khi m £ 0 .
B. Hàm số có 3 cực trị khi m > 0 .
C. Hàm số có 1 cực trị khi m < 0 .
D. Hàm số có ít nhất hai cực trị.
Câu 24. Đồ thị của hàm số 3 2
y = ax + bx + cx + d có hai điểm cực trị là gốc tọa độ O(0;0) và điểm
A (2;-4) thì phương trình của hàm số là: A. 3 2
y = x -3x . B. 3
y = x -3x . C. 3 2
y = -3x + x . D. 3
y = -3x + x . 1
Câu 25: Số điểm cực trị của đồ thị hàm số 3
y   x x  7 là ? 3 A. 1 B. 0 C. 3 D. 2
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN
Câu 1: Đồ thị hàm số sau là của hàm số nào? A. 3 2
y  x  3x 1 B. 4 2
y  x  2x  2 C. 4 2
y x  2x  2 D. 3 2
y x  3x 1 1
Câu 2: Số điểm cực trị của đồ thị hàm số 3
y   x x  7 là ? 3 A. 1 B. 0 C. 3 D. 2 x 1
Câu 3: Cho hàm số sau: y
, những mệnh đề nào đúng trong các mệnh đề sau ? x  3
(1) : Hàm số luôn nghịch biến trên D   \   3
(2) : Đồ thị hàm số có 1 tiệm cận đứng là x  1; 1 tiệm cận ngang là y  3
(3) : Hàm số đã cho không có cực trị.
(4): Đồ thị hàm số nhận giao điểm I 3; 
1 của 2 đường tiệm cận làm tâm đối xứng. A. (1),(3),(4) B. (3),(4) C. (2),(3),(4) D. (1), (4) x
Câu 4: Hàm số y
đồng biến trên khoảng nào ? 2 x 1 A.  ;    1 B. 1; C.  1;   1 D.  ;    1 và 1; Câu 5: Cho hàm số 4 2
y x  2x  2 . Giá trị cực đại của hàm số bằng ? A. 2 B. 1 C. -1 D. 0
Câu 6: Tìm giá trị nhỏ nhất của hàm số 3 2
y x  3x  9x  6 trên  4;  4
A. Min f x  21
B. Min f x  14
C. Min f x  11
D. Min f x  70  4;4 4;4  4;  4 4;4 2 x  3mx
Câu 7: Tìm m để hàm số y
(C) cắt đường thẳng y mx  7 d  tại 2 điểm phân biệt? x  3 19 19 19 19 A. m B. m
và m  1 C. m D. m  và m  1 12 12 12 12 2 2x 1
Câu 8: Đồ thị hàm số y
có bao nhiêu tiệm cận ? 2 x  2x A. 1 B. 0 C. 2 D. 3
Câu 9. Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn đáp án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? A. 2
y  x x 1. B. 3
y  x  5x 1. C. 4 2
y x  2x  3. D. 4 2
y  x  2x  3. Câu 10. Hàm số 3 2
y x  2x x 1 đồng biến trên khoảng nào ?  1   2   1  A. ;   và 1;. B. ;   . C.   ;1  và 2;. D.  ;1. 3     3   3 
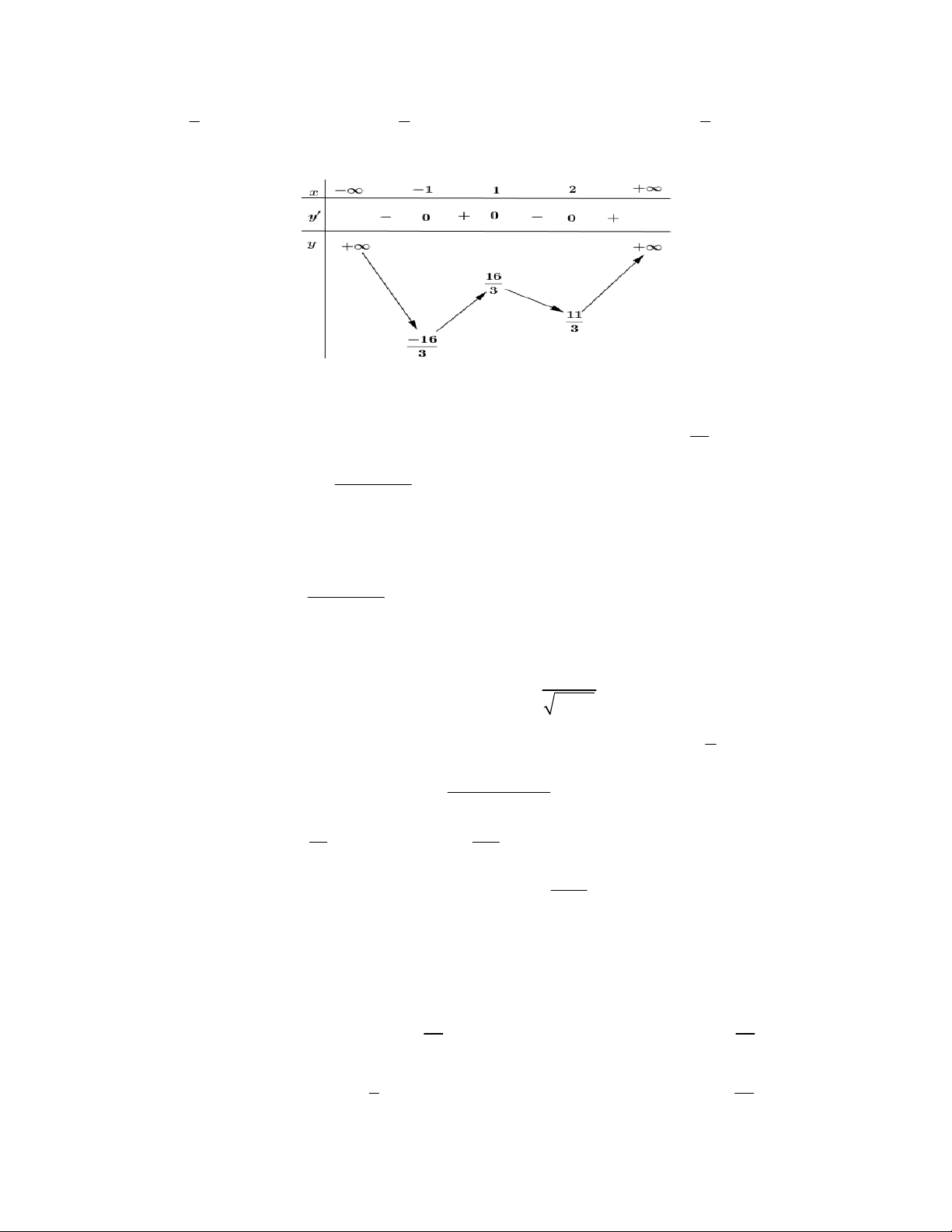
Câu 11. Cho hàm số y f (x) xác định và liên tục trên  và có bảng biến thiên sau:
Khẳng định nào sau đây là khẳng định sai ?
A. Hàm số có ba cực trị. B. Hàm số đạt giá trị cực đại tại x  1  và x  2. 16
C. Hàm số đạt giá trị cực đại tại x  1. D. Giá trị cực đại của hàm số y  . CÑ 3 x x
Câu 12. Cho hàm số f x 2 2 3 
. Khẳng định nào sau đây là khẳng định đúng ? x  2
A. Hàm số luôn nghịch biến trên . B. Hàm số luôn nghịch biến trên  \   2 .
C. Hàm số luôn đồng biến trên . D. Hàm số đồng biến trên khoảng  ;  2   và  2;  . 2
x ax b
Câu 13. Cho hàm số y  với ,
a b là các số thực. Đồ thị hàm số đã cho có điểm cực đại x 1 là (0
A ;1). Tính giá trị của biểu thức P  2a  . b
A. P  3.
B. P  6.
C. P  5.
D. P  4. x  3
Câu 14. Tìm đường tiệm cận ngang của đồ thị hàm số y  . 2 x 1 1 A. y  3. B. y  2. C. y  1.
D. y  . 2 2 20x 10x  3
Câu 15. Tìm giá trị nhỏ nhất của hàm số y  trên đoạn  3;  1  . 2 3x  2x 1   13 153 A. 7. B. . C. . D. 6. 2 22 4  x
Câu 16. Biết rằng đường thẳng y x cắt đồ thị hàm số y
tại điểm duy nhất, kí hiệu điểm đó 3 x
là x ; y . Tìm y . 0 0  0
A. y  4.
B. y  6.
C. y  2. D. y  1.  0 0 0 0 Câu 17. Cho hàm số 3 2
y x  2x x  6 , khẳng định nào sau đây đúng về tính đơn điệu của hàm số:  1    1  
A. Hàm số đồng biến trên   ;1  và ; 
B. Hàm số chỉ nghịch biến trên ;    3   3   1   1  
C. Hàm số đồng biến trên 1;  
D. Hàm số nghịch biến trên  ;    1 và ;    3   3  3  x
Câu 18. Cho hàm số y f x 
có đồ thị (C). Khẳng định nào sau đây là đúng? 2 x  2
A. Đồ thị (C) có một tiệm cận đứng là x  2 và không có tiệm cận ngang
B. Đồ thị (C) có đúng một tiệm cận đứng là x  2 và một tiệm cận ngang là y  0 .
C. Đồ thị (C) có hai tiệm cận đứng là x  2; x   2 và một tiệm cận ngang là y  0 .
D. Đồ thị (C) có hai tiệm cận đứng là x  2; x   2 và không có tiệm cận ngang. Câu 19. Hàm số 3 2
y  2x  9x 12x  4 nghịch biến trên khoảng nào? A.   ;1  B. 1;2 C. 2;3 D. 2;
Câu 20. Trong các hàm số sau hàm số nào đồng biến trên  ?
A. y  3sin 1 4x B. 2
y x  3x  4 C. 4 2
y x x 1 D. 3
y x  5x 13 Câu 21. Cho hàm số 4 2
y  2x  4x  3 và các kết quả sau: (I): y  3
 tại x  0 (II): y  3 tại x  1 (III): y  3 tại x  1 CT CD CD Kết luận nào đúng: A. Chỉ I B. Chỉ II C. Chỉ III D. Cả I, II, III 2 x  3
Câu 22. Tìm giá trị nhỏ nhất của hàm số y  trên đoạn 2;4 x 1 19
A. min y  6 B. min y  2  C. min y  3  D. min y  2;4 2;4 2;4 2;4 3 5x  3
Câu 23. Tìm giá trị nhỏ nhất của hàm số y  trên 3;5 x  2 28 3 A. min y
B. min y   C. min y  2  D. min y  5 3;5 3 3;5 2 3;5 3;5
Câu 24. Cho đồ thị của hàm số 4 2
y ax bx c (a  0) như hình vẽ. Khẳng định nào sau đây là
khẳng định đúng ?
A. a  0, b  0, c  0. B. a  0, b  0, c  0. C. a  0, b  0, c  0. D. a  0, b  0, c  0. 2x 1
Câu 25. Tìm các khoảng đồng biến của hàm số y  . x  2  1   1  A.  ;
 2 và 2; . B. ;    và ; .    2   2   1   1  C. ;     và  ; .   D.  ;  2   và  2;  .  2   2 
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN
Câu 1. Số điểm cực trị của hàm số 3 2
y ax bx cx d (a  0) có thể là ? A. 3.
B. 0 hoặc 2. C. 1 hoặc 2.
D. 0 hoặc 1 hoặc 2. 4
Câu 2. Tìm giá trị nhỏ nhất của hàm số f x  1 sin 2x  . 2 sin 2x
A. 3. B. 15. C. 17. D. 4. 2 x  5x 15
Câu 3. Điểm M thuộc đồ thị C của hàm số y
và M có tọa độ là các số nguyên. x  3
Hỏi có bao nhiêu điểm M thỏa mãn bài toán ?
A. 4 B. 7. C. 3. D. 6 1 Câu 4. Cho hàm số 3 2
y x mx  2m  
1 x 1 . Mệnh đề nào sau đây là sai ? 3 A. m
 1 thì hàm số có hai cực trị
B. Hàm số luôn luôn có cực đại và cực tiểu. C. m
  1 thì hàm số có cực đại và cực tiểu. D. m
 1 thì hàm số có cực trị. 2x 1
Câu 5. Tập xác định của hàm số y  là: 3  x  1 
A. D   B. D   ;3
  C. D   ; \     3
D. D  3;  2  x 1
Câu 6. Tìm m để đồ thị hàm số y
có đúng một đường tiệm cận đứng 2
x  2mx  3m  4 A. m  5;  1  ;  4 B. m  1;
 4 C. m ;    1  4; D. m  1  ;  4 Câu 7. Hàm số 3 2
y  2x  9x 12x  4 nghịch biến trên khoảng nào ? A.   ;1  B. 1;2 C. 2;3 D. 2;
Câu 8. Đồ thị hàm số 3 2
y  x  6x 13x  6 có bao nhiêu điểm cực trị ? A. 0 B. 1 C. 2 D. 3
Câu 9. Với giá trị nào của m để đường thẳng y x m đi qua trung điểm của đoạn nối hai điểm cực
trị của đồ thị hàm số 3 2
y x  6x  9x ?
A. m  0
B. m  1
C. m  2 D. m  3
Câu 10. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y x  3x 1 trên đoạn  1;  4 là:
A. max y  51; min y  3 
B. max y  51;min y  1  1;  4 1;4  1;  4  1;  4
C. max y  51;min y  1 
D. max y  1;min y  1  1;  4  1;  4  1;  4  1;  4
Câu 11. Cho hàm số y f (x) có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị hàm số có tiệm cận đứng y  1
 và tiệm cận ngang x  2. 
B. Đồ thị hàm số có duy nhất một tiệm cận.
C. Đồ thị hàm số có ba tiệm cận.
D. Đồ thị hàm số có tiệm cận đứng x  1 và tiệm cận ngang y  2.  2 x x 1
Câu 12. Hàm số y
nghịch biến trên khoảng nào ? x 1 A.  
;1 . B. 1;2. C. 2;. D.  ;0  . m
Câu 13. Kí hiệu m và M lần lượt là GTNN, GTLN của hàm số 2
y x  12  3x . Tính tỉ số . M m 1 m 1 m 1 m 1 A.   . B.  . C.   . D.  . M 4 M 2 M 2 M 4
Câu 14. Số giá trị cực trị của hàm số 4 2
y x  2x  3 là: A. 1 B. 2 C. 3 D. Vô số
Câu 15. Giá trị lớn nhất của hàm số 3 2
y x  2x x  4 là: 104 A. -4 B.C. 100 D. Không tồn tại 27
Câu 16. Số điểm cực trị của hàm số 3 2
y x  3x  3x  6 là: A. 0 B. 1 C. 2 D. Vô số 2x 1
Câu 17. Chọn phát biểu đúng khi nói về tiệm cận của đồ thị hàm số y  . x  2
A. Tiệm cận ngang là đường thẳng y  2
B. Tiệm cận đứng là đường thẳng x  2
C. Tiệm cận đứng là đường thẳng y  2
D. Tiệm cận ngang là đường thẳng y  2 1
Câu 18. Khoảng đồng biến của hàm số 3 2
y x  2x  3x  5 là: 3 A.  ;3   B. 1; C. 1;3 D. 3; 1 1
Câu 19. Tâm đối xứng của đồ thị hàm số 3 2
y x  2x  3x  có tọa độ là: 3 3  1   1   1   1  A. I 2;    B. I 2;   C. I 2;   D. I 2;      3   3   3   3 
Câu 20. Hàm số nào dưới đây có bảng biến thiên sau: x  0 2  y '  0  0  y  CÑ y  3  A. 3 2
y x  3x 1. B. 3 2
y  x  3x 1. C. 4 2
y x  4x  3. D. 3 2
y  2x  6x  4.
Câu 21. Đồ thị hàm số nào sau đây không có ba tiệm cận ? x  3 2 x x 1 3 x x 1 3 x  2 A. y  . B. y  . C. y  . D. y . 2 2x  2x 2 4  x 3 x 1 3 2 x  3x  4 x
Câu 22. Cho hàm số f x 1 
. Khẳng định nào sau đây là khẳng định đúng ? 2  5x
A. Hàm số luôn nghịch biến trên .   2   2 
B. Hàm só luôn nghịch biến trên hai khoảng ;    và ;  .    5   5 
C. Hàm số đồng biến trên .   2   2 
D. Hàm số đồng biến trên hai khoảng ;    và ;  .    5   5 
Câu 23. Cho hàm số f x  2  x  2  x. Khẳng định nào sau đây là khẳng định đúng ?
A. min f x  0 và max f x  3 2.
B. min f x  2 và max f x  3 2.  2;  2  2;2    2;  2  2;2  
C. min f x  2 và max f x  2 2.
D. min f x  1 và max f x  3 2.  2;  2  2;  2 2;2  2;  2 3 x  3x  2
Câu 24. Giao điểm hai đường tiệm cận của đồ thị hàm số y  có tọa độ là ? 3 x  3 A. T  3
1; 3. B. T  3 3; 
1 . C. T 1;3. D. T 3;  1 .
Câu 25. Tìm tất cả giá trị thực của tham số m sao cho hàm số 3 2
y x  3x  3mx  20m 17 đồng biến trên .  A. m  ;
 . B. m1;. C. m 1;    .
D. m  ;1  . 
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN 2x 1
Câu 1. Hàm số y  luôn: x 1
A. Đồng biến trên 
B. Nghịch biến trên 
C. Đồng biến trên từng khoảng xác định
D. Nghịch biến trên từng khoảng xác định
Câu 2. Giá trị cực đại của hàm số 3 2
y x  3x  5x  7 là: 3   2 6 3   2 6 32 6 32 6 A. B. C. D.  3 3 9 9 2 x  x  2
Câu 3: Khoảng đồng biến của hàm số y  là: x 1 A.  ;
 3 và 1; B.  ;   
1 và 3; C. 3; D. 1;3 4
Câu 4: Đường thẳng d : y  x 3 cắt đồ thị (C) của hàm số y  2 x tại hai điểm. Gọi x
x , x x  x là hoành độ giao điểm của hai đồ thị hàm số, tính y  3y . 1 2  1 2  2 1 A. y  3y  25 B. y  3y  1  0 C. y  3y  1 D. y  3y  2  7 2 1 2 1 2 1 2 1 1
Câu 5. Một vật rơi tự do với phương trình chuyển động 2
S gt , trong đó 2
g  9,8m / s và t tính 2
bằng giây (s). Vận tốc của vật tại thời điểm t  5s bằng:
A. 25m / s
B. 49m / s
C. 10m / s
D. 18m / s 2x 1
Câu 6. Hàm số y  luôn: x 1
A. Đồng biến trên 
B. Nghịch biến trên 
C. Đồng biến trên từng khoảng xác định
D. Nghịch biến trên từng khoảng xác định
Câu 7. Hàm số y  m   2
3 x  2mx  3 không có cực trị khi: m  0 A. m  3 B.C. m  0 D. m  3 m  3
Câu 8. Hàm số nào sau đây đồng biến trên  ?
A. y  tan x . B. y  4 x  2 2 x . C. y  3
x  3x  1 . D. y  3 x  2 . 2 x 1
Câu 9. Gọi Q là giá trị lớn nhất và K là giá trị nhỏ nhất của hàm số y
trên đoạn 1;2. Khi đó x 1 24Q  27K
giá trị của biểu thức 1997 là: 2 3929 3925 3927 3923 A.B.C.D.  2 2 2 2
Câu 10: Đồ thị hàm số nào sau đây luôn nằm dưới trục hoành A. 4 2 y  x  3x 1 B. 3 2
y  x  2x  x 1 C. 4 2
y  x  2x  2 D. 4 2 y  x  4x 1 2 x  x  2
Câu 11: Khoảng đồng biến của hàm số y  là: x 1 A.  ;
 3 và 1; B.  ;   
1 và 3; C. 3; D. 1;3 4
Câu 12: Đường thẳng d : y  x 3 cắt đồ thị (C) của hàm số y  2 x tại hai điểm. Gọi x
x , x x  x là hoành độ giao điểm của hai đồ thị hàm số, tính y  3y . 1 2  1 2  2 1 A. y  3y  1 B. y  3y  1  0 C. y  3y  25 D. y  3y  2  7 2 1 2 1 2 1 2 1 1
Câu 13: Tính tất cả các giá trị của tham số m để hàm số y  m   3 2 1 x  x  2m   1 x  3 có cực 3 trị ?  3   3   3   3  A. m   ;0 
B. m   ;0 \     1 C. m   ;0  
D. m   ;0 \   1 2     2   2   2   
Câu 14. Kết luận nào sau đây là không đúng về đồ thị hàm số 3 2
y ax bx cx d a  0 ?
A. Đồ thị hàm số bậc ba luôn cắt trục hoành tại ít nhất một điểm.
B. Đồ thị hàm số bậc ba nhận điểm có hoành độ là nghiệm của PT y"  0 làm tâm đối xứng.
C. Nếu PT y '  0 có 2 nghiệm phân biệt thì đồ thị hàm số bậc ba có 1 điểm cực đại, 1 điểm cực tiểu.
D. Đồ thị hàm số bậc ba không có điểm cực trị khi và chỉ khi phương trình y '  0 vô nghiệm. 2 x  3x 1
Câu 15. Hàm số y  đồng biến trên: x 1 A.  ;   
1 và 1; B.  ;   
1  1; C. đồng biến với mọi x D. 1;  1
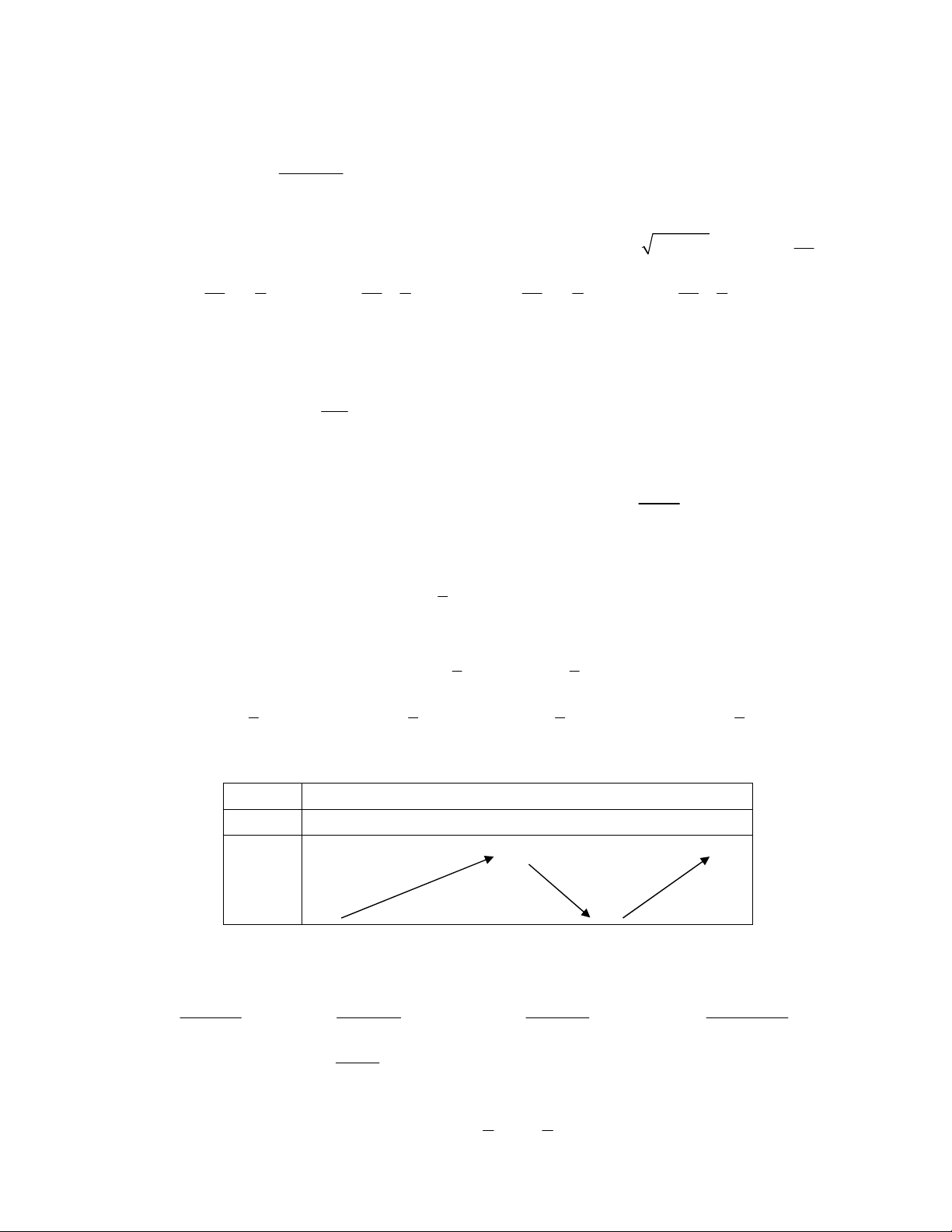
Câu 16. Cho đồ thị hàm số y f x 4 2
x  2x  3 như hình vẽ. Từ đồ thị suy ra được số nghiệm của phương trình 4 2
x  2x  3  m với m 3;4 là:
A. 3 B. 2 C. 4 D. 6
Câu 17. Biết đồ thị hàm số 4 2
y x bx c chỉ có một điểm cực trị là
điểm có tọa độ 0; 
1 thì b và c thỏa mãn điều kiện nào ?
A. b  0 và c  1 
B. b  0 và c  1 
C. b  0 và c  0
D. b  và c tùy ý.
Câu 18. Với giá trị nào của m thì đường thẳng y x m đi qua trung điểm của đoạn nối 2 điểm cực
trị của đồ thị hàm số 3 2
y x  6x  9x ? A. 0 B. 1 C. 2 D. 3
Câu 19. Gọi M và m lần lượt là GTLN và GTNN của hàm số 2
y x 1 x trên tập xác định. Khi
đó M m bằng ? A. 1 B. 2 C. 3 D. đáp số khác
Câu 20. Đồ thị của hàm số 3
y x  3x cắt:
A. đường thẳng y  3 tại hai điểm
B. đường thẳng y  4  tại hai điểm. 5
C. đường thẳng y  tại ba điểm
D. trục hoành tại một điểm. 3
Câu 21: Cho hàm số y  f x xác định, liên tục trên  và có bảng biến thiên: x  1  1 2  y' + 0 + 0 - 0 + y 9  20  3  5
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có ba cực trị. 9 3
B. Hàm số có giá trị lớn nhất bằng
và giá trị nhỏ nhất bằng  20 5
C. Hàm số đồng biến trên khoảng   ;1 
D. Hàm số đạt cực đại tại x  2 và đạt cực tiểu tại x  1 x 1
Câu 22: Đồ thị hàm số y 
có bao nhiêu đường tiệm cận ? x 1 A. 0 B. 1 C. 2 D. 3 Câu 23: Cho hàm số 3
y  x  3x 1. Viết phương trình đường thẳng qua hai điểm cực trị của đồ thị hàm số. A. y  2  x 1 B. y  2  x 1 C. y  2x 1 D. y  2x 1
Câu 24: Đồ thị hàm số bậc 2 và đồ thị hàm số bậc 4 trùng phương có chung đặc điểm nào sau đây
A. Đều tồn tại cả điểm cực đại và điểm cực tiểu B. Đều có tâm đối xứng
C. Đồ thị hàm số đều có dạng parabol
D. Đều có trục đối xứng Câu 25: Hàm số 4 2
y x  2x  1
A. Nghịch biến trên ( -1 ; 1) B. Đồng biến trên (1;) C. Đồng biến trên ( ;  0)
D. Nghịch biến trên (-1 ; 0)
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN
Câu 1: Tổng của GTLN và GTNN của hàm số 3 2
y x  3x  9x  35 trên đoạn 4;4   là : A. -1 B. 48 C. -26 D. 23 ax  2
Câu 2: Hãy xác định a,b để hàm số y
có đồ thị như hình vẽ: x b
A. a  1 ;b  2 
B. a b  2
C. a  1;b  2
D. a b  2 
Câu 3: Giá trị nhỏ nhất của hàm số y = sinx( 1 + cosx) trên đoạn [ 0;  ] là: 2 3 A. 1 B. C. 0 D. 2 4 2 2x 1
Câu 4: Phương trình tiếp tuyến của đồ thị y 
tại điểm có hoành độ x  1 là: x A. y  x  2 B. y  3x  3 C. y  x  2 D. y  x  3
Câu 5: Giá trị lớn nhất của hàm số   2
f x  x  2x  3 trên đoạn 0;  3 là: A. 3 B. 18 C. 2 D. 6
Câu 6: Giá trị nhỏ nhất của hàm số   2 f x  x  2x  5 là: A. 5 B. 2 2 C. 2 D. 3
Câu 7: Giá trị lớn nhất và GTNN của hàm số 3 2
y x  3x  9x  40 trên đoạn  5;  5 lần lượt là A. 45; 115  . B. 13; 115  . C. 45;13 . D. 115;45 . Câu 8: Cho hàm số 4 2
y x  2x 1024 . Trong các mệnh đề sau, mệnh đề nào sai?
A. Đồ thị hàm số qua ( A 0; 1024)  .
B. Hàm số có 1 cực tiểu.
C. lim f (x)   ;
 lim f (x)   .
D. Đồ thị có 2 điểm có hoành độ thỏa mãn y ''  0 . x x
Câu 9: Tìm GTLN của hàm số 2
y x  5  x trên  5; 5   ? A. 5. B. 10 . C. 6. D. Đáp án khác.
Câu 10: Phương trình 3 2
x  3x m m có 3 nghiệm phân biệt khi A. m  21  . B. 1   m  2 . C. 1   m  2 . D. 2   m 1.
Câu 11: Phương trình tiếp tuyến của đường cong (C) 3
y x  2x tại điểm có hoành độ x  1  là
A. y  x  2 .
B. y x  2 .
C. y  x  2 .
D. y x  2 . Câu 12: Cho hàm số 3 2
y x  6x mx 1 đồng biến trên 0; khi giá trị của m là A. m  0 . B. m  0 . C. m  12 . D. m  12 .
Câu 13: Điểm nào sau đây thuộc đồ thị hàm số 3
y x  3x  5 mà hoành độ là nghiệm của phương trình y ''  0 ? A. 0;0 . B. 1;3 . C.  1  ;  1 . D. 0;5.
Câu 14: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? x 1 x 1 A. y  B. y  x  2 x  2 2x 1 x 1 C. y  D. y  2x  2 x  2 Câu 15: Hàm số 4 2
y  x  8x  7 có bao nhiêu giá trị cực trị ? A. 0 B. 1 C. 2 D. 3
Câu 16: Hỏi có tất cả các giá trị nguyên của m để đồ thị hàm số 1 3 2 y  x  mx   2
2m  3m  3 x  2016 có 2 cực trị: 3 A. 3 B. 4 C. 5 D. 6 2
Câu 17: Tìm tất cả các giá trị của m để hàm số 3 2
y  x  mx  4mx  2016 có hai điểm cực trị thỏa 3 x  x  3 . 1 2 A. m  9
B. Không tồn tại giá trị m thỏa mãn yêu cầu bài toán m  1  C.D. m  1  m  9 
Câu 18: Tìm tọa độ giao điểm M của đồ thị   2x 1 C : y 
và đường thẳng d : y  3 x 1 A. M  4  ;3 B. M 3;4 C. M 4;3 D. M 3; 4   x  5
Câu 19: Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số y  2 x 1
A. Đồ thị hàm số không có đường tiệm cận đứng B. x  1 và x  1  C. x  1 D. x  1 
Câu 20: Viết phương trình tiếp tuyến của đồ thị hàm số   4 2
f x  x  x 1 tại điểm có hoành độ x  1 A. y  6x  3 B. y  6  x  3 C. y  6x  3 D. y  6  x  3
Câu 21: Cho hàm số y f x xác định và liên tục trên R và có bảng biến thiên: x  1  2  f ' x + 0 + 0 - 5 f x 0  
Mệnh đề nào sau đây là sai:
A. Hàm số đồng biến trên  ;  2
B. Hàm số nghịch biến trên 2;
C. Giá trị lớn nhất của hàm số trên R là 5 khi x  2 D. Hàm số đạt cực trị tại x  1  Câu 22: Cho hàm số 4 2
y x  4x  5 và các khoảng: (I)  2;0 , (II) 0; 2 , (III)  2;
Hàm số đồng biến trên khoảng nào ? A. I và II B. II và III C. III và I D. chỉ I
Câu 23: Giao điểm có hoành độ là số nguyên của đồ thị hàm số y  3x  2 và đồ thị hàm số 3
y x x 1 là: A. 0;  1 B. 0;2 C. 1;5 D.  1  ;  1 x  2
Câu 24: Tìm lỗi sai trong bài toán khảo sát hàm số y
của một bạn học sinh như sau: x 1 Bài giải
1. Tập xác định:  \  1  2. Sự biến thiên: 3 
+) Chiều biến thiên y '  x  2 1
y' không xác định khi x  1 ; y' luôn âm với mọi x  1
vậy hàm số nghịch biến trên  ;    1 và  1  ;
+) Cực trị: Hàm số đã cho không có cực trị +) Tiệm cận: lim y   ;  lim y   x 1 x 1  
Do đó đường thẳng x  1  là tiệm cận đứng lim y  1  x
Vậy đường thẳng y  1  là tiệm cận ngang +) Bảng biến thiên: x  1   y' - - 1   y  1 
A. Bài giải trên sai ở giai đoạn tìm điều kiện xác định B. Bài giải trên đạo hàm sai
C. Bài giải trên sai ở giai đoạn tìm tiệm cận D. Bài giải trên sai bảng biến thiên Câu 25: Cho hàm số 4 2
y  3x  6x 1 . Kết luận nào sau đây là đúng ? A. y  2  B. y  1 C. y  1  D. y  2 CD CD CD CD
SỞ GD-ĐT QUẢNG NGÃI ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BA TƠ Môn: Toán Giải Tích 12A1. Năm học: 2017 -2018
Họ và tên học sinh: ( Thời gian làm bài: 45 phút)
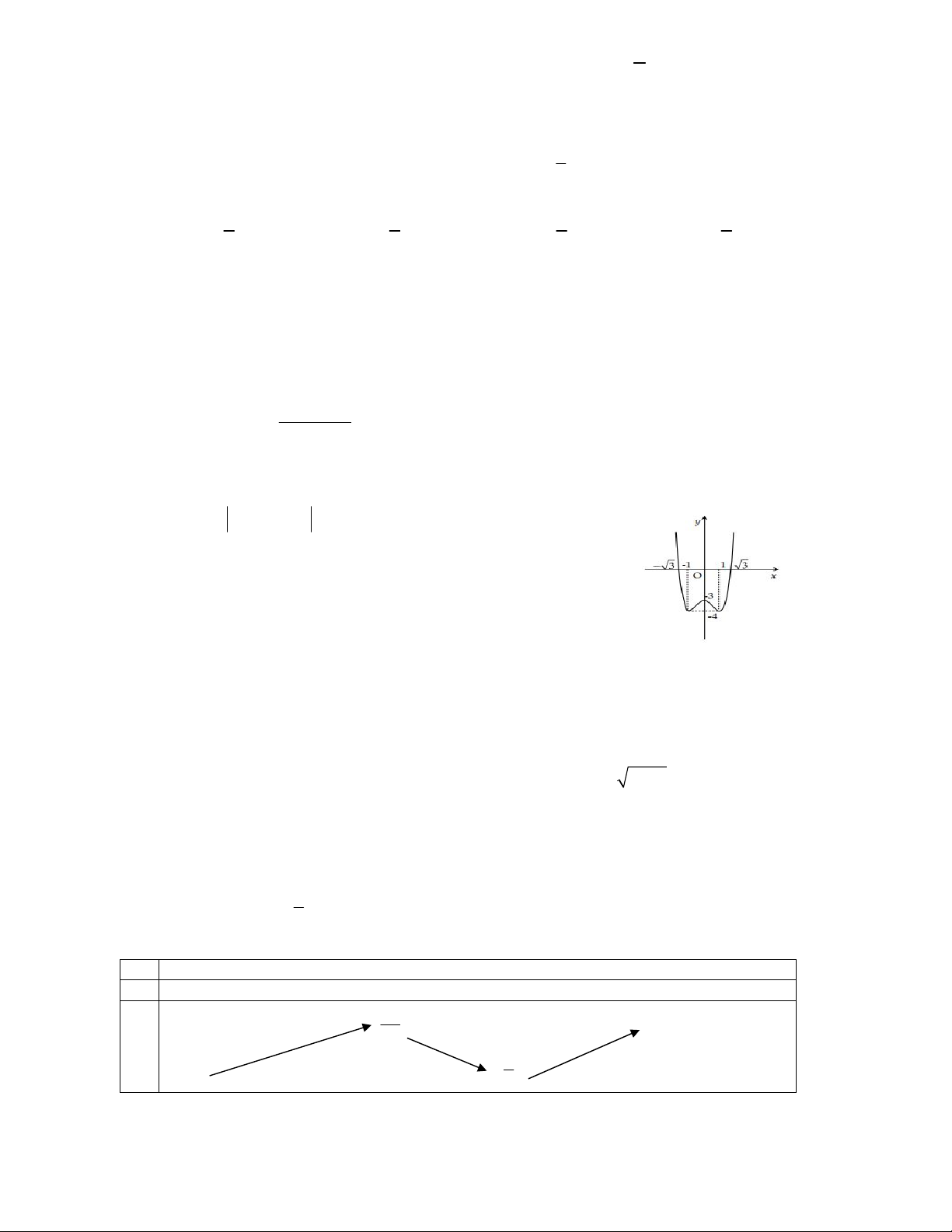
……………………………………………. CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐÁP ÁN CÂU 14 15 16 17 18 19 20 21 22 23 24 25 ĐÁP ÁN 2 x Câu 1: 5
Tìm giá trị nhỏ nhất của hàm số y  trên đoạn 0; 2   . x  3 5 1
A. min y   .
B. min y   .
C. min y  2 .
D. min y  10 .  x 0;2   3  x 0;2   3  x 0;2    x 0;2   Câu 2: Cho hàm số 3
y  x  3x  2016 . Trong các giá trị sau giá trị nào là giá trị cực trị của hàm số? A. 2 B. 2018 C. 2017 D. -1
Câu 3: Tìm tọa độ điểm cực tiểu M của đồ thị hàm số 3 y  x  3x  2 A. M  1  ;0 B. M 1;0 C. M  1  ;4 D. M 1;4
Câu 4: Gọi M , N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số: 2 y  x  4  x .
Giá trị của biểu thức M  2N A. 2 2  2 B. 2 2  4 C. 2 2  2 D. 2 2  4
Câu 5: Trong các kết quả sau, kết quả nào nêu đúng cả hai đường thẳng đều là tiệm cận của đồ thị x  5 hàm số y  x 1
A. x 1; y    1 B. x  1  ; y    2 C. x 1; y   1
D. x 1; y   2 x  2016
Câu 6: Đồ thị hàm số y 
có số đường tiệm cận là: 2 x  5 A. 1 B. 2 C. 3 D. 4
Câu 7. Cho hàm số y f x có đạo hàm tại x . Tìm mệnh đề đúng? 0
A. Nếu f ' x  0 thì hàm số đạt cực trị tại x 0  0
B. Hàm số đạt cực trị tại x thì f x  0 0  0
C. Nếu hàm số đạt cực trị tại x thì f ' x  0 0  0
D. Hàm số đạt cực trị tại x thì f ' x đổi dấu khi qua x 0 0 1 1
Câu 8. Một học sinh khảo sát sự biến thiên 3 2
y x x  2x  2 như sau: 3 2
I. Tập xác định: D R x  1  II. Sự biến thiên: 2
y '  x x  2; y '  0    x  2 lim y   ;  lim y   x x III. Bảng biến thiên: x  -1 2  y' + 0  0 + y 19  6 4   3
IV. Vậy hàm số đồng biến trên  ;   
1  2; , nghịch biến trên khoảng  1  ;2
Lời giải trên sai từ bước nào?
A. Lời giải trên sai từ giai đoạn I
B. Lời giải trên sai từ giai đoạn II
C. Lời giải trên sai từ giai đoạn III
D. Lời giải trên sai ở giai đoạn IV a x
Câu 9. Xác định a,b để hàm số y
có đồ thị như hình vẽ: x b
A. a  2;b  1
B. a  1;b  2 C. a  1;  b  2 D. a  2;  b  1 
Câu 10. Hàm số nào sau đây không có cực trị: A. 2
y x B. 3
y x  3x C. 4 2
y x  2x D. 2 y  3x
Câu 11. Hàm số nào sau đây không có GTLN trên đoạn  2;  2 ? 1 x 1
A. y  x B. 3
y x  2 C. 4 2
y x x D. y  2 x 1 x
Câu 12. Số nguyên dương m nhỏ nhất để đường thẳng y  x m cắt đồ thị hàm số C 3 : y  2  x
tại hai điểm phân biệt là:
A. m  1
B. m  0
C. m  2
D. m  3 2x  3 x  7
Câu 13. Cho hai hàm số y  và y
. Tập hợp các giá trị của tham số m để hai 2 x m  4 x  5
đường tiệm cận đứng của 2 đồ thị hàm số trên trùng nhau là? A.  1;   1 B.  3;   3 C.  2;   2 D.   0
Câu 14. Số điểm cực trị của đồ thị hàm số 4 2
y ax bx c a  0;b  0 là: A. 0 B. 2 C. 1 D. 3
Câu 15: Cho hàm số y f x xác định, liên tục trên R và có bảng biến thiên như sau: x  1   y' + 0 + y  1 
Khẳng đinh nào đúng trong các khẳng đinh sau?
A. Hàm số đạt cực trị tại x =1
B. Hàm số đồng biến trên R
C. Tập giá trị của hàm số là[1;)
D. Hàm số có giá trị nhỏ nhất bằng 1 Câu 16: Hàm số 3
y x  3x  2 đồng biến trên tập nào sau đây ? A. R B. ( ;  1  ) C. (1;) D. R   1 
Câu 17: Đồ thị bên là đồ thị của hàm số nào trong các hàm số sau A. 2
y  x  2x 1 B. 2
y x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y x  2x 1 1 5
Câu 18: Tìm tổng các giá trị cực trị của hàm số 3 2
y x x  6x 1 3 2 17  11 67 17 A. B. C. D. 3 2 6 3 1
Câu 19: Tìm giá trị lớn nhất của hàm số 2
y  4x   2 trên đoạn [-1;2] x 29 A. 3 B. 1 C. D. Không tồn tại 2 2x 1
Câu 20: Cho hàm số y
có đồ thị (C) và đường thẳng (d) y  x m . Tìm m để (C) cắt (d) x  3
tại 2 điểm phân biệt A và B sao cho AB  2 14 A. -1 B. 1 C. -2 D. 2
Câu 21: Đồ thị hàm số y  3 x  2
3x  2x  1 cắt đồ thị hàm số y  2
x  3x  1 tại hai điểm phân
biệt A, B. Khi đó độ dài AB là bao nhiêu ? A. AB  2 . B. AB  2 2 . C. AB  3 . D. AB  1 .
Câu 22: Tìm giá trị lớn nhất của hàm số f (x)  3cos 3x  2cos 2x  9cos x 1 A. -11 B. 13 C. 16 D. -3
Câu 23: Trong các hình sau có cùng chu vi, hình nào có diện tích lớn nhất?
A. Hình tam giác đều B. Hình vuông C. Hình chữ nhật D. Hình tròn Câu 24: Cho hàm số 4 2
f (x)  x mx  2m  4 . Tìm m để đồ thị của hàm số đã cho cắt trục hoành tại bốn điểm phân biệt. m  2
A. m  2
B. m  4 C.
D. 2  m  4 m  4 2x
Câu 25: Tìm tiệm cận đứng của đồ thị hàm số y  ? 2 x  3x A. x  0; x  3 B. y  3 C. y  0 D. x  3