Đề kiểm tra 45 phút ĐS&GT 11 chương 5 năm 2018 – 2019 trường Phan Đăng Lưu – TT Huế

Đề kiểm tra 45 phút ĐS&GT 11 chương 5 năm học 2018 – 2019 trường THPT Phan Đăng Lưu – TT Huế mã đề 134, nội dung kiểm tra thuộc chủ đề đạo hàm, đề kiểm tra gồm 02 trang với 20 câu trắc nghiệm, học sinh làm bài kiểm tra trong thời gian 1 tiết học.

54 27 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

2 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/2 - Mã đề thi 134
SỞ GD&ĐT THỪA THIÊN HUẾ
TRƯỜNG THPT PHAN ĐĂNG LƯU
KIÊM TRA 45 PHÚT
MÔN: GIẢI TÍCH 11
Thời gian làm bài: 45 phút
(20 câu trắc nghiệm)
Mã đề thi 134
Họ và tên học sinh: …......................................................... Lớp: ..................
Câu 1: Phương trình tiếp tuyến với đồ thị
32
:26 3Cy x x
có hệ số góc nhỏ nhất là
A.
650xy
. B.
650xy
. C.
670xy
. D.
630xy
.
Câu 2: Hình bên là đồ thị của hàm số
yfx . Biết rằng tại các điểm
A
,
B
, C đồ thị hàm số có
tiếp tuyến được thể hiện trên hình vẽ bên dưới.
Mệnh đề nào dưới đây đúng?
A.
A
CB
f
xfxfx

. B.
B
AC
f
xfxfx

.
C.
A
BC
f
xfxfx

. D.
CAB
f
xfxfx

.
Câu 3: Một chất điểm chuyển động theo quy luật
23
13St t t . Vận tốc của chuyển động đạt giá
trị lớn nhất khi
t
bằng bao nhiêu
A.
3t . B. 4t . C. 2t . D. 1t .
Câu 4: Tính đạo hàm của hàm số
2
sin 3yx .
A.
6cos3
x
. B.
3cos6
x
. C.
6sin6
y
x
. D.
3sin6
y
x
.
Câu 5: Cho hàm số
 
32
22
3
m
f
xxmxx
. Để đạo hàm
f
x
bằng bình phương của một
nhị thức bậc nhất thì giá trị
m là
A.
1
hoặc
4
. B. Không có giá trị nào.
C. 1 hoặc 1. D. 4 hoặc 4 .
Câu 6: Tính đạo hàm của hàm số
1
sin 2
y
x
.
A.
2
2cos
sin 2
x
y
x

. B.
2
2cos2
sin 2
x
y
x
. C.
2
cos 2
sin 2
x
y
x

. D.
2
2cos2
sin 2
x
y
x

.
Câu 7: Đạo hàm của hàm số
2
sin 2yx trên là ?
A.
2sin4yx

. B.
2cos4yx
. C.
2sin4yx
. D.
2cos4yx

.
Câu 8: Tìm số hạng không chứa
x
trong khai triển nhị thức Newton của
2
3
2
n
x
x



0x , biết
rằng
123
1. 2. 3. ... 256
n
nnn n
CCC nC n
(
k
n
C
là số tổ hợp chập
k
của
n
phần tử).
A.
489888
. B.
4889888
. C.
48988
. D.
49888
.
Câu 9: Tìm số tiếp tuyến của đồ thị hàm số
32
461yx x , biết tiếp tuyến đó đi qua điểm

1; 9 .M
A.
0
. B. 1. C. 2 . D.
3
.
O
x
y
A
B
C
C
x
A
x
B
x
Trang 2/2 - Mã đề thi 134
Câu 10: Cho đồ thị hàm số
32
22yx x x có đồ thị

C
. Gọi
1
x
,
2
x
là hoành độ các điểm
M
,
N
trên

C mà tại đó tiếp tuyến của

C vuông góc với đường thẳng
2019yx
. Khi đó
12
x
x
bằng
A. 1 . B.
4
3
. C.
4
3
. D.
1
3
.
Câu 11: Biết hàm số
2
f
xfx có đạo hàm bằng 19 tại 1
x
và đạo hàm bằng 1000 tại 2x .
Tính đạo hàm của hàm số
4
f
xfx tại 1
x
.
A. 2018 . B. 2019 . C. 2018 . D. 2019 .
Câu 12: Gọi đường thẳng
y
ax b
là phương trình tiếp tuyến của đồ thị hàm số
21
1
x
y
x
tại điểm
có hoành độ
1
x
. Tính
Sab
.
A. 1S  . B. 1S . C.
1
2
S
. D. 2S .
Câu 13: Hàm số

2
2
1
x
y
x
có đạo hàm là
A.

2
2
2
1
x
x
y
x

.
B.

2
2
2
1
x
x
y
x
.
C.
22yx
 . D.

2
2
2
1
x
x
y
x
.
Câu 14: Đạo hàm của hàm số

2
23
f
xx
bằng biểu thức nào sau đây?
A.
2
2
6
22 3
x
x
.
B.
2
3
23
x
x
. C.
2
3
23
x
x
. D.
2
1
22 3
x
.
Câu 15: Phương trình tiếp tuyến của đường cong
32
32yx x tại điểm có hoành độ
0
1x là
A.
97
y
x
. B.
97
y
x
. C.
97
y
x
. D.
97
y
x
.
Câu 16: Có bao nhiêu điểm thuộc đồ thị hàm số
21
1
x
y
x
thỏa mãn tiếp tuyến với đồ thị có hệ số
góc bằng
2019
?
A. Vô số. B.
0
. C. 1. D. 2 .
Câu 17: Phương trình tiếp tuyến của đồ thị hàm số
1
2
x
y
x
tại điểm có hoành độ bằng 3 là
A. 313yx . B. 35yx . C. 35yx. D. 313yx.
Câu 18: Cho hàm số
32
265yxx có đồ thị
C
. Phương trình tiếp tuyến của

C
tại điểm
M
thuộc

C
và có hoành độ bằng
3
là
A.
18 49yx
. B.
18 49yx
. C.
18 49yx
. D.
18 49yx
.
Câu 19: Hệ số góc
k
của tiếp tuyến đồ thị hàm số
3
1yx tại điểm
1; 2M
là
A.
5k
.
B.
4k
.
C.
3k
.
D.
12k
.
Câu 20: Cho hàm số

2
1
x
fx
x
. Tính
f
x
?
A.


2
1
1
fx
x
. B.


2
1
1
fx
x
. C.


2
2
1
fx
x
. D.


2
2
1
fx
x
.
----------- HẾT ----------
| 1/2
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT THỪA THIÊN HUẾ KIÊM TRA 45 PHÚT
TRƯỜNG THPT PHAN ĐĂNG LƯU MÔN: GIẢI TÍCH 11
Thời gian làm bài: 45 phút
(20 câu trắc nghiệm) Mã đề thi 134
Họ và tên học sinh: …......................................................... Lớp: ..................
Câu 1: Phương trình tiếp tuyến với đồ thị C 3 2
: y  2x  6x  3 có hệ số góc nhỏ nhất là
A. 6x y  5  0 .
B. 6x y  5  0 .
C. 6x y  7  0 .
D. 6x y  3  0 .
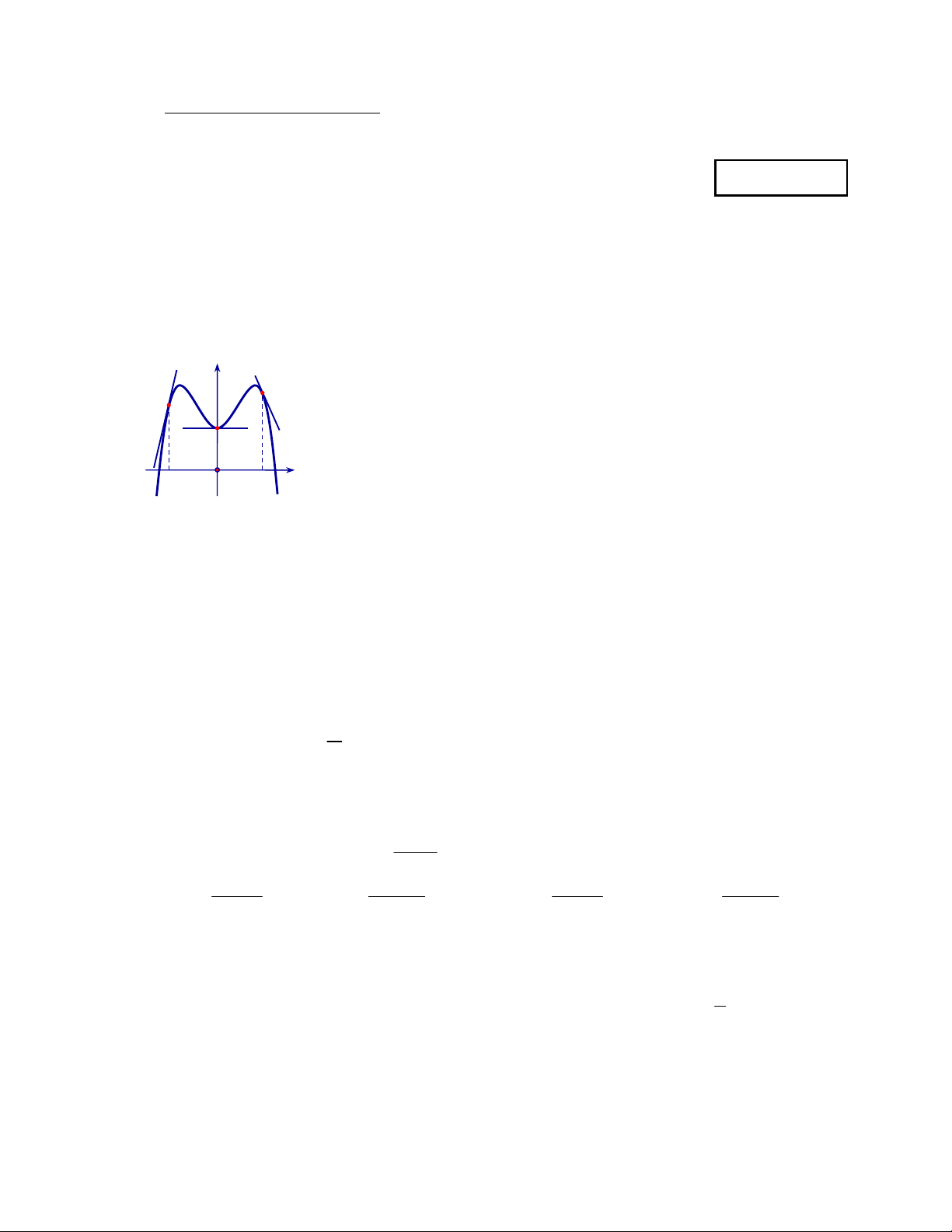
Câu 2: Hình bên là đồ thị của hàm số y f x . Biết rằng tại các điểm A , B , C đồ thị hàm số có
tiếp tuyến được thể hiện trên hình vẽ bên dưới. y B C A x x x C O A B x
Mệnh đề nào dưới đây đúng?
A. f  x f x f x .
B. f  x f x f x . B   A  C A   C   B
C. f  x f x f x .
D. f  x f x f x . C   A  B A   B   C
Câu 3: Một chất điểm chuyển động theo quy luật S t 2 3
1 3t t . Vận tốc của chuyển động đạt giá
trị lớn nhất khi t bằng bao nhiêu A. t  3 . B. t  4. C. t  2. D. t  1.
Câu 4: Tính đạo hàm của hàm số 2 y  sin 3x .
A. y  6 cos 3x .
B. y  3cos 6x .
C. y  6sin 6x .
D. y  3sin 6x . m
Câu 5: Cho hàm số f x 3 
x  m   2
2 x x  2 . Để đạo hàm f  x bằng bình phương của một 3
nhị thức bậc nhất thì giá trị m là A. 1 hoặc 4 .
B. Không có giá trị nào. C. 1 hoặc 1. D. 4  hoặc 4 . 1
Câu 6: Tính đạo hàm của hàm số y  . sin 2x 2 cos x 2 cos 2x cos 2x 2 cos 2x A. y   . B. y  . C. y   . D. y   . 2 sin 2x 2 sin 2x 2 sin 2x 2 sin 2x
Câu 7: Đạo hàm của hàm số 2
y  sin 2x trên  là ?
A. y  2sin 4x .
B. y  2 cos 4x .
C. y  2sin 4x .
D. y  2 cos 4x .  3 n
Câu 8: Tìm số hạng không chứa x trong khai triển nhị thức Newton của 2 2x  
  x  0 , biết  x  rằng 1 2 3
1.C  2.C  3.C  ... n
nC  256n ( k
C là số tổ hợp chập k của n phần tử). n n n n n A. 489888 . B. 4889888 . C. 48988 . D. 49888 .
Câu 9: Tìm số tiếp tuyến của đồ thị hàm số 3 2
y  4x  6x 1, biết tiếp tuyến đó đi qua điểm M  1  ; 9  . A. 0 . B. 1. C. 2 . D. 3 .
Trang 1/2 - Mã đề thi 134
Câu 10: Cho đồ thị hàm số 3 2
y x  2x 2
x có đồ thị C. Gọi x , x là hoành độ các điểm M , N 1 2
trên C mà tại đó tiếp tuyến của C vuông góc với đường thẳng y  x  2019. Khi đó x x 1 2 bằng 4 4 1 A. 1. B. . C. . D. . 3 3 3
Câu 11: Biết hàm số f x  f 2x có đạo hàm bằng 19 tại x 1 và đạo hàm bằng 1000 tại x  2 .
Tính đạo hàm của hàm số f x  f 4x tại x 1. A. 20  18. B. 2019 . C. 2018 . D. 20  19. 2x 1
Câu 12: Gọi đường thẳng y ax b là phương trình tiếp tuyến của đồ thị hàm số y  tại điểm x 1
có hoành độ x  1. Tính S a b . 1 A. S  1  . B. S 1. C. S  . D. S  2 . 2 x  2 2
Câu 13: Hàm số y  có đạo hàm là 1 x 2 x  2x 2 x  2x 2 x  2x A. y  . B. y  . C. y  2  x  2 . D. y  . 1 x2 1 x2 1 x2
Câu 14: Đạo hàm của hàm số f x 2
 2  3x bằng biểu thức nào sau đây? 2 6  x 3x 3x 1 A. . B. . C. . D. . 2 2 2  3x 2 2  3x 2 2  3x 2 2 2  3x
Câu 15: Phương trình tiếp tuyến của đường cong 3 2
y x  3x  2 tại điểm có hoành độ x  1 là 0
A. y  9x  7 .
B. y  9x  7 .
C. y  9x  7 .
D. y  9x  7 . 2x 1
Câu 16: Có bao nhiêu điểm thuộc đồ thị hàm số y
thỏa mãn tiếp tuyến với đồ thị có hệ số x 1 góc bằng 2019 ? A. Vô số. B. 0 . C. 1. D. 2 . x 1
Câu 17: Phương trình tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ bằng 3  là x  2 A. y  3  x 13. B. y  3  x  5.
C. y  3x  5.
D. y  3x 13. Câu 18: Cho hàm số 3 2 y  2
x  6x  5 có đồ thị C. Phương trình tiếp tuyến của C tại điểm M
thuộc C và có hoành độ bằng 3 là
A. y  18x  49 .
B. y  18x  49 .
C. y  18x  49 .
D. y  18x  49 .
Câu 19: Hệ số góc k của tiếp tuyến đồ thị hàm số 3
y x 1 tại điểm M 1;2 là A. k  5 . B. k  4 . C. k  3. D. k 12 . x
Câu 20: Cho hàm số f x 2 
. Tính f  x ? x 1 1 1 2 2
A. f  x  .
B. f  x  .
C. f  x  .
D. f  x  . x  2 1 x  2 1 x  2 1 x  2 1
----------- HẾT ----------
Trang 2/2 - Mã đề thi 134