Đề kiểm tra chuyên đề Toán 10 lần 2 năm 2019 – 2020 trường Quang Hà – Vĩnh Phúc

SỞ GD&ĐT VĨNH PHÚC
ĐỀ KIỂM TRA CHUYÊN ĐỀ LẦN II
TRƯỜNG THPT QUANG HÀ NĂM HỌC 2019 - 2020
Đề 1. Môn: Toán; Khối 10
Thời gian làm bài: 120 phút, không kể thời gian phát đề
Câu 1. (1,0 điểm): Tìm các tập hợp sau:
a/ 2;5 4;7 b/ 1;5 \ 3;7
Câu 2. (1,0 điểm): Xác định a, b để đồ thị hàm số y  ax  b đi qua hai điểm A0;3 và B1;  1
Câu 3. (1,0 điểm): Xác định Parabol 2
y  ax  bx  c biết rằng Parabol đó đi qua điểm A 0;5 và đỉnh I 2;  1
Câu 4. (2,0 điểm): Giải các phương trình sau:
a/ 2x  5  3x - 2
b/ 4x - 7  2x - 5
c/ x 1  x 1  1
Câu 5. (1,0 điểm): Cho phương trình 2
x  2x  m  0 . Tìm m để phương trình có hai nghiệm phân biệt x ; x thỏa mãn: 2 2 x  x 10 . 1 2 1 2 2 2
x  xy  y  4
Câu 6. (1,0 điểm): Giải hệ phương trình sau: 
x  xy  y  2
Câu 7. (2,0 điểm): Trong mặt phẳng tọa độ Oxy, cho 3 điểm (
A 1; 2); B(-2;6); C(4; 4)
a/ Chứng minh 3 điểm A, B, C không thẳng hàng
b/ Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. 2 1
Câu 8. (0,5 điểm): Cho tam giác ABC. Gọi D, E lần lượt là các điểm thỏa mãn: BD  BC; AE  AC . 3 4 Điểm K trên đoạ AD
n thẳng AD sao cho B, K, E thẳng hàng. Tìm tỉ số . AK 
 x  y 2 2
x  xy  y  3  3 2 2
x  y   2
Câu 9. (0,5 điểm): Giải hệ phương trình :  2 2
x y  x  2x 12  0
---------Hết----------- SỞ GD&ĐT VĨNH PHÚC
ĐỀ KIỂM TRA CHUYÊN ĐỀ LẦN II
TRƯỜNG THPT QUANG HÀ NĂM HỌC 2019 - 2020
Đề 2. Môn: Toán; Khối 10
Thời gian làm bài: 120 phút, không kể thời gian phát đề
Câu 1. (1,0 điểm): Tìm các tập hợp sau: a/ 1;4 3;  8 b/ 2;6 \ 4;8
Câu 2. (1,0 điểm): Xác định a, b để đồ thị hàm số y  ax  b đi qua hai điểm A0;-3 và B2;5
Câu 3. (1,0 điểm): Xác định Parabol 2
y  ax  bx  c biết rằng Parabol đó đi qua điểm A 0;2 và đỉnh I 1  ;1
Câu 4. (2,0 điểm): Giải các phương trình sau:
a/ 3x 1  2x - 4
b/ 5  x  x - 3
c/ x  3  x  1
Câu 5. (1,0 điểm): Cho phương trình 2
x  3x  m  0 . Tìm m để phương trình có hai nghiệm phân biệt x ; x thỏa mãn: 2 2 x  x 17 . 1 2 1 2 2
x  x  y 2 3  y  28
Câu 6. (1,0 điểm): Giải hệ phương trình: 
x  xy  y 11
Câu 7. (2,0 điểm): Trong mặt phẳng tọa độ Oxy, cho 3 điểm ( A 1  ;3); B(2; 5  ); C(3;4)
a/ Chứng minh 3 điểm A, B, C không thẳng hàng
b/ Tìm tọa độ điểm D sao cho tứ giác ABDC là hình bình hành.
Câu 8. (0,5 điểm): Cho tam giác ABC có trọng tâm G và điểm N thỏa mãn NB  3NC  0 . Gọi P PA
là giao điểm của AC và GN , tính tỉ số . PC 2 2
2x  xy  y 5x  y  2  0
Câu 9. (0,5 điểm): Giải hệ phương trình  2 2
x  y  x  y  4  0
---------Hết----------- SỞ GD&ĐT VĨNH PHÚC
ĐÁP ÁN KIỂM TRA CHUYÊN ĐỀ LẦN II TRƯỜNG THPT QUANG HÀ
NĂM HỌC 2019 – 2020
Đề 1. Môn: Toán; Khối 10 Câu Ý Nội dung Thang điểm 1 a
2;54;7 4;5 0.5 b
1;5\3;7  1;3 0.5 2 b   3 0.5
Ta có hệ phương trình:  a  b 1 b   3 0.25   a  2  Vậy y  2  x  3 0.25 3
Câu 3. (1,0 điểm): Xác định Parabol 2
y  ax  bx  c biết rằng Parabol đó đi
qua điểm A0;5 và đỉnh I 2;  1 Ta có hệ phương trình: 0.5  c  5 
4a  2b  c 1  b    2 2a c  5 0.25 b   4 a 1  Vậy Parabol là: 2
y  x  4x  5 0.25 4 a
Câu 4. (2,0 điểm): Giải các phương trình sau:
a/ 2x  5  3x - 2
2x  5  3x  2 0.5
2x  5  3x - 2   2x  5  3  x  2 x  7 0.25   3   x   5 b  5  0.5 2x  5  0  x 
4x - 7  2x - 5     2 4x  7   2x-52 2
4x 24x32  0  5 0.25 x   2       x  l  x 4 2  x  4  tm c
x 1  x 1  1 0.25 Đk: x 1 x 1  1 x 1
 x 1 1 x 1 2 x 1 1  2 x 1 0.25 1  4x   1 5
 x  tm KL: Nghiệm phương trình 5 x  4 4 5
Câu 5. (1,0 điểm): Cho phương trình 2
x  2x  m  0 . Tìm m để phương trình
có hai nghiệm phân biệt x ; x thỏa mãn: 2 2 x  x 10 . 1 2 1 2
Để phương trình có 2 nghiệm phân biệt  '  0 1 m  0  m 1 0.25 x  x  2  0.25 Theo Vi ét ta có: 1 2  
x .x  m  1 2 Ta có: x  x
10  x  x 2 2 2  2x x 10 0.25 1 2 1 2 1 2   2 2
 2m 10  m  3  tm 0.25 6 2 2
x  xy  y  4
Câu 6. (1,0 điểm): Giải hệ phương trình sau: 
x  xy  y  2 
 x  y2  xy  4  0.25
x  y  S 2     Đặt ;S 4P  x  y   xy  2 xy  P 2 S  P  4 0.25 ta có:  S  P  2 S  3;  P  5 l  0.25   S  2; P  0  tm
x  2; y  0 0.25
Giải ra được   x  ; 0 y  2 7
Câu 7. (2,0 điểm): Trong mặt phẳng tọa độ Oxy, cho 3 điểm ( A 1; 2); (
B -2;6); C(4; 4) a
a/ Chứng minh 3 điểm A, B, C không thẳng hàng 0.5 Ta có: AB  ( 3  ;4); AC  (3;2) 3  4 0.5 Mà:   Ba điểm ; A ;
B C không thẳng hàng 3 2 b
b/ Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. 0.5 Gọi D  ( ; x y)
Để tứ giác ABCD là hình bình hành  AB  DC  ( 3
 ;4)  (4  x; 4  y) x  7 0.5    D ; 7 0 y  0 8
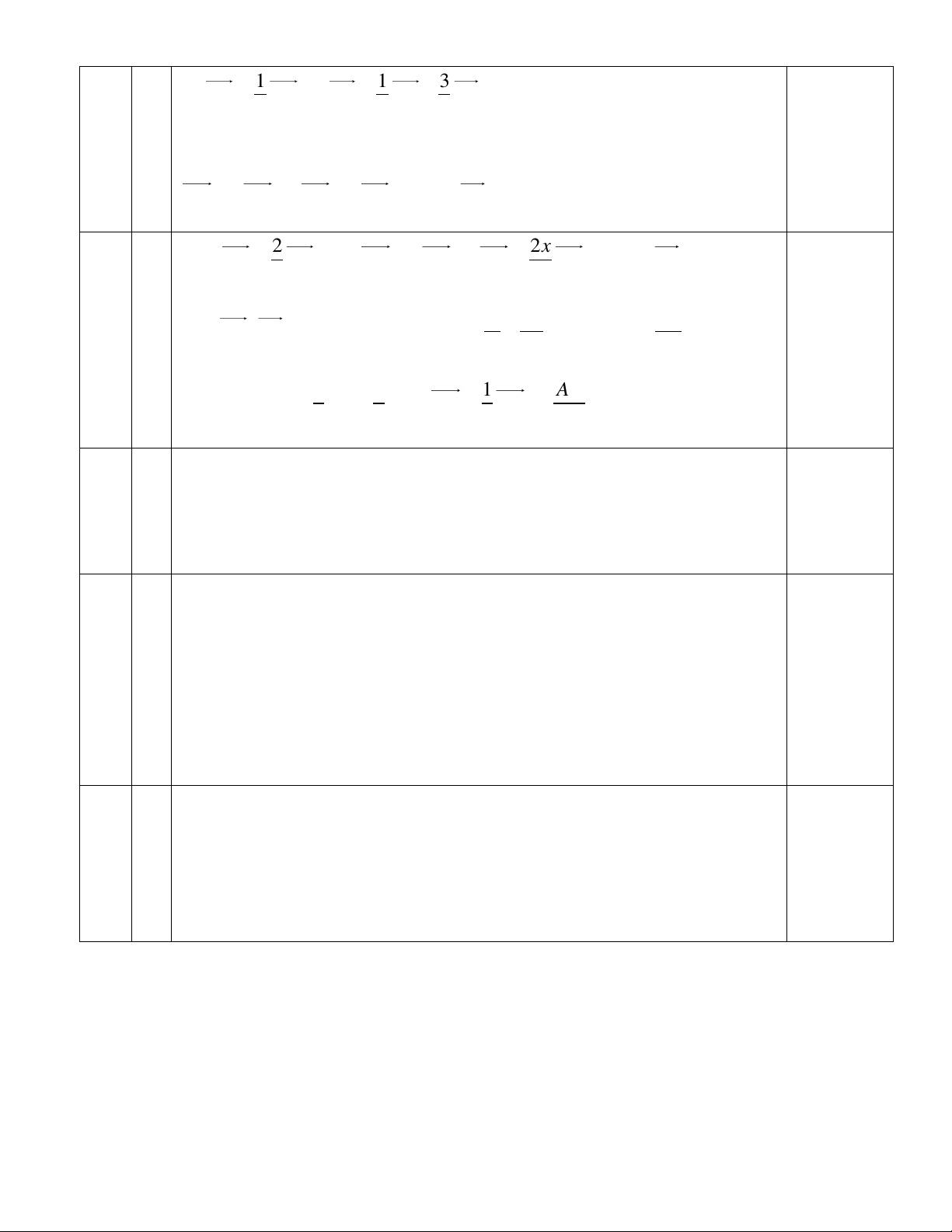
Câu 8. (1,0 điểm): Cho tam giác ABC. Gọi D, E lần lượt là các điểm thỏa mãn: 2 1 BD  BC; AE 
AC . Điểm K trên đoạn thẳng AD sao cho B, K, E thẳng 3 4 AD hàng. Tìm tỉ số . AK 0,25 1 1 3 Vì AE  AC  BE  BC  BA   1 4 4 4 Giả sử:
AK  x AD  BK  xBD  1 x BA   1 2 2x Mà: BD 
BC nên AK  x AD  BK 
BD  1 x BA 3 3 m 2x 3m
Do . BC; BA không cùng phương nên:   0; 1 x   0 0,25 4 3 4 1 8 1 AD Từ đó suy ra x  ; m  Vậy AK  AD   3 3 9 3 AK 9
Câu 9. (0,5 điểm): Giải hệ phương trình 
 x  y 2 2
x  xy  y  3  3 2 2
x  y   2  2 2
x y  x  2x 12  0
x  y 2 2
x  xy  y  3  3 2 2
x  y   2
 x  y 2 2
x  xy  y  2 2
 3(x  y)  3(x  y )  2 3 3 2 2
 x  y  3(x  y)  3x  3y  2 0,25 3 2 3 2
 x  3x  3x 1  y  3y  3y 1 3 3
 (x 1)  (y 1)  x 1  y 1  y  x  2
Thế y  x  2 vào phương trình (2) ta có 2 2 3 2
x (x  2)  x  2x 12  0  x  x  2x 12  0 . 0,25 x  3 2
 (x  3)(x  2x  4)  0  x  3  y 1. Hệ có nghiệm  y  1 SỞ GD&ĐT VĨNH PHÚC
ĐÁP ÁN KIỂM TRA CHUYÊN ĐỀ LẦN II TRƯỜNG THPT QUANG HÀ
NĂM HỌC 2019 – 2020
Đề 2. Môn: Toán; Khối 10 Câu Ý Nội dung Thang điểm 1 a 1;43;  8  3;4 0.5 b
2;6\4;8  2;4 0.5 2 b   3  0.5
Ta có hệ phương trình: 
2a  b  5 b   3  0.25   a  4
Vậy y  4x  3 0.25 3
Câu 3. (1,0 điểm): Xác định Parabol 2
y  ax  bx  c biết rằng Parabol đó đi qua
điểm A0;2 và đỉnh I 1  ;1 Ta có hệ phương trình: 0.5  c  2 
a  b  c  1  b    1 2a c  2 0.25 b   2 a 1  Vậy Parabol là: 2
y  x  2x  2 0.25 4 a
Câu 4. (2,0 điểm): Giải các phương trình sau:
a/ 3x 1  2x - 4
3x 1  2x  4 0.5
3x 1  2x - 4   3x 1  2  x  4 x  5  0.25   3  x   5 b x  3  0  x  3 0.5
b/ 5  x  x - 3     5   x   x-32 2
x  5x  4  0 x  3 0.25   x 1 
l  x  4  x  4  tm c
x  3  x  1 0.25 Đk: x  0 x  3  1 x
 x  3 1 x  2 x  2  2 x 0.25  x 1
 x 1 tm KL: Nghiệm phương trình x=1 5
Câu 5. (1,0 điểm): Cho phương trình 2
x  3x  m  0 . Tìm m để phương trình có
hai nghiệm phân biệt x ; x thỏa mãn: 2 2 x  x 17 . 1 2 1 2 0.25 Để 9
phương trình có 2 nghiệm phân biệt   '  0  9  4m  0  m  4 x  x  3  0.25 Theo Vi ét ta có: 1 2  
x .x  m  1 2 Ta có: x  x
17  x  x 2 2 2  2x x 17 0.25 1 2 1 2 1 2   2 3
 2m 17  m  4  tm 0.25 6 2
x  x  y 2 3  y  28
Câu 6. (1,0 điểm): Giải hệ phương trình: 
x  xy  y 11 
 x  y2 3x  y 2xy  28  0.25
x  y  S 2     Đặt ;S 4P  x  y   xy 11 xy  P 2
S  3S  2P  28 0.25 ta có:  S  P 11 S  1  ; 0
P  21 tm 0.25   S  5; P  6  tm x  3  ; y  7 0.25
x   ;7 y  3 
Giải ra được   x  2; y  3  x  3; y  2 7
Câu 7. (2,0 điểm): Trong mặt phẳng tọa độ Oxy, cho 3 điểm ( A 1  ;3); ( B 2; 5  ); C(3;4) a
a/ Chứng minh 3 điểm A, B, C không thẳng hàng 0.5 Ta có: AB  (3; 8  ); AC  (4;1) 3 8  0.5 Mà:   Ba điểm ; A ;
B C không thẳng hàng 4 1 b
b/ Tìm tọa độ điểm D sao cho tứ giác ABDC là hình bình hành. 0.5 Gọi D  ( ; x y)
Để tứ giác ABDC là hình bình hành  AB  CD  (3; 8  )  (x3; y 4) x  6 0.5    D6; 4   y  4  8
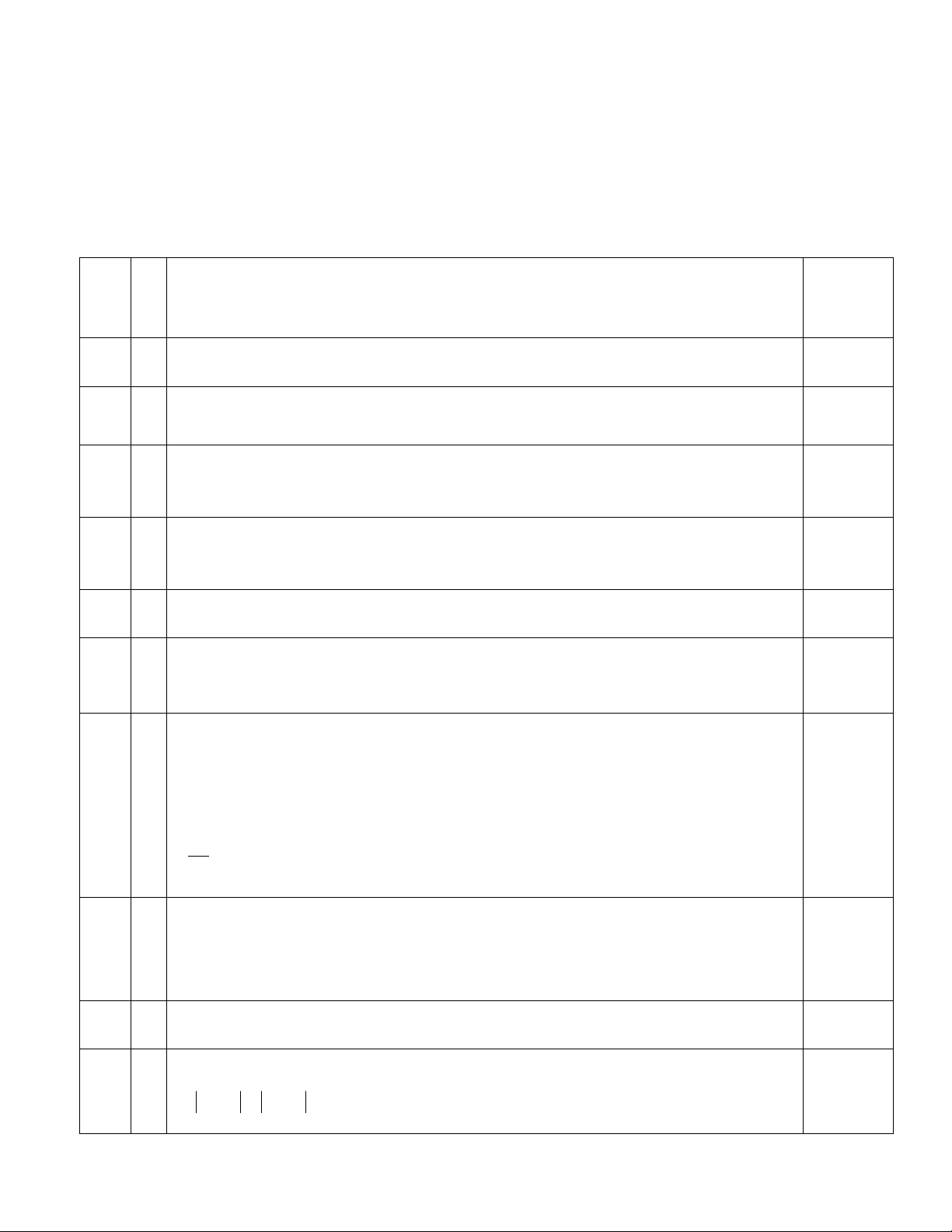
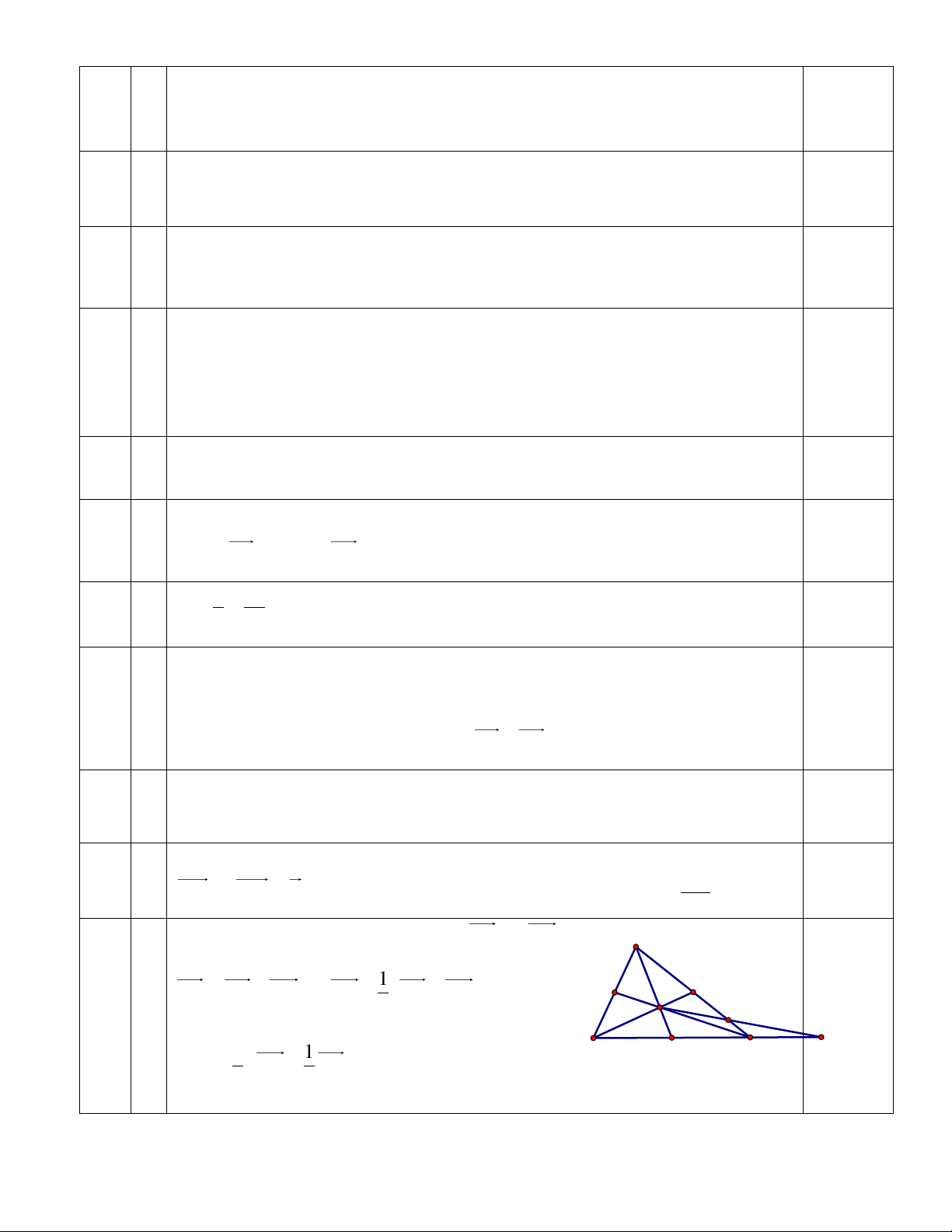
Câu 8. (1,0 điểm): Cho tam giác ABC có trọng tâm G và điểm N thỏa mãn PA
NB  3NC  0 . Gọi P là giao điểm của AC và GN , tính tỉ số . PC
Gọi M là trung điểm của cạnh BC. Đặt AP  k AC . A 1
GP  AP  AG  k AC   AB  AC G 3 P 0,25 N  1  1 B M C  k  AC  AB   .  3  3 1 1
GN  GM  MN  AM  BC  AB AC 7 5
 AC  AB  AC  AB 3 6 6 6 Ba điểm G, ,
P N thẳng hàng nên hai vectơ G ,
P GN cùng phương. Do đó 1 1 1 k   k  2 1 7 4 4 3 3 3     k  
 k   AP  AC 7 5 7 5 3 15 5 5  0,25 6 6 6 4 PA
 AP  AC   4 5 PC 9
Câu 9. (0,5 điểm): Giải hệ phương trình 2 2
2x  xy  y 5x  y  2  0  2 2
x  y  x  y  4  0 Ta có: 2 2 2 2
2x  xy  y  5x  y  2  0  y  2xy  y  xy  2x  x  2 y  4x  2  0
 y y  2x  
1  x  y  2x  
1  2 y  2x   1  0    y   x y  2x  
1  y  x  2 2
 0  y  2x1 0,25 Như thế:
y  2  x          x   2  x2 2 2 2
 x  2  x x xy y x y   4  0 2 5 2 0    2 2
x  y  x  y  4  0
y  2x 1   x   2x  2 2
1  x  2x   1  4  0
y  2  x  2
2x  4x  2  0
 y  2x1  0,25  2  5
 x  x  4  0 x  1  y  1  4    x     5   13    y   5     Vậy hệ có nghiệm  ; x y là   4 13 1;1 ; ;    5 5 
Document Outline

• de_1-kscdtoan_1o-lan_2_152202021
• de_2-kscd_toan_1o-_lan_2_152202021
• dap_an-de_12-kscdtoan_1o-lan_2_152202021