

Preview text:
TRƯỜNG THPT CHUYÊN BẮC NINH
ĐỀ KIỂM TRA CUỐI HÈ NĂM 2019 TỔ TOÁN – TIN
Môn thi: Toán 10 chuyên
Thời gian: 150 phút (không kể thời gian giao đề)
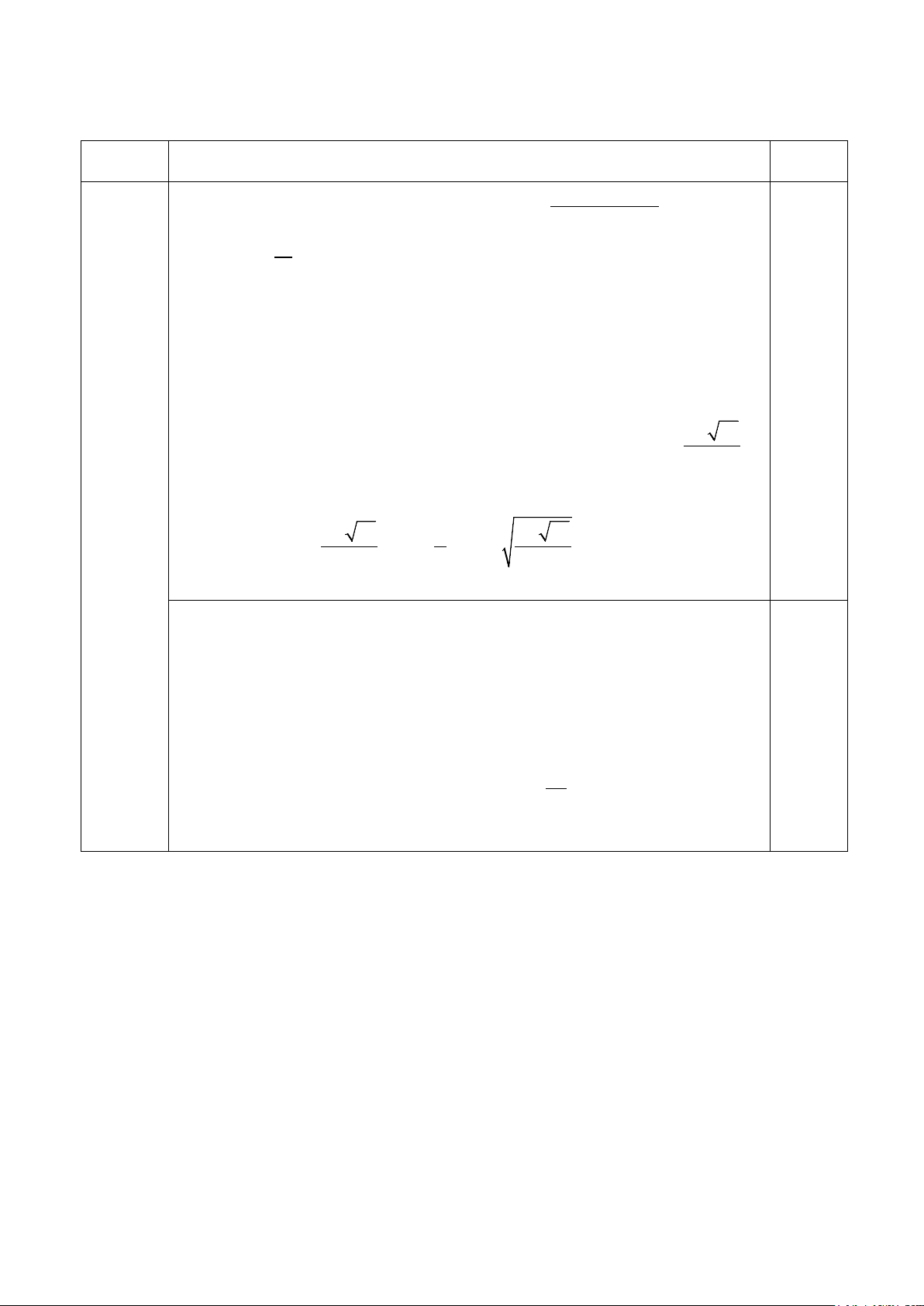
(Đề thi gồm 01 trang) Câu 1 (2,0 điểm). Cho phương trình 2 8 + 42 + 55 m x x = 2 4x + 23x + 33
a) Giải phương trình khi m =1.
b) Tìm m để phương trình có 4 nghiệm phân biệt. Câu 2 (3,0 điểm)
Cho hình vuông ABCD có tâm .
O Đường thẳng d quay quanh O, cắt hai cạnh AD và
BC lần lượt ở E và F (không trùng với các đỉnh của hình vuông). Qua E và F lần lượt
kẻ đường thẳng song song với BD và AC chúng cắt nhau tại I. Kẻ IH vuông góc với
EF tại H. Chứng minh rằng:
a) Điểm I chạy trên đoạn A . B
b) Điểm H thuộc đường tròn cố định và đường thẳng IH đi qua một điểm cố định.
Câu 3 (1,0 điểm). Cho hai số 2a > b > 0. Chứng minh rằng 64 2a + ≥ 5.
(2a −b)(b +3)2 Câu 4 (2,0 điểm).
a) Cho tập X ={1,2,3,..., }
2020 . Chứng minh rằng trong số 1011 phần tử bất kì của tập X
luôn có hai phần tử nguyên tố cùng nhau.
b) Chứng minh rằng tồn tại vô số số nguyên dương n thỏa mãn 5n −1 chia hết cho .n
Câu 5 (2,0 điểm). Giả sử phương trình 2
ax + bx + c = 0(a ≠ 0) có các nghiệm x , x . 1 2 Đặt n n
S = x + x n∈ n , . 1 2
a) Chứng minh: aS +bS + = − cS n n n− 0. 1 2
b) Áp dụng tính A = ( + )8 +( − )8 1 3 1 3
------------ Hết ------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm. ĐÁP ÁN TOÁN 10 Câu Nội dung Điểm a) Khi m 1 1 điểm = 1, ta có phương trình 2 8x + 42x + 55 = ĐK 2 4x + 23x + 33 11 x ≠ 3 − ; x ≠ − 4
PT ⇔ (2x + 5)(4x + ) 11 (4x + ) 11 (x + 3) =1
⇔ (2x + 5)(x + 3)(4x + )2 11 =1
⇔ (4x +10)(4x +12)(4x + )2 11 = 8 Đặt ( x + )2 4
3 = t,(t ≥ 0), phương trình trở thành 2 1 33 t t 8 0 t ± − − = ⇔ = , 2
Câu 1 đối chiếu đk, (2điểm) ta có ( + + x + )2 1 33 1 1 33 4 11 = ⇔ x = 11 − ± 2 4 2
b) Ta có ( x + )( x + )( x + )2 2
4 10 4 12 4 11 = 8m ⇒ t − t −8m = 0 (1) 1 điểm
với t = ( x + )2 4 11 ,t ≥ 0.
PT đã cho có 4 nghiệm phân biệt khi và chỉ khi PT (1) có hai nghiệm ∆ > + > t 0 1 32m 0 dương phân biệt 1 ⇔ S > 0 ⇔ 1 > 0 ⇔ − < m < 0. 32 P 0 > 8 − m > 0 1 điểm Câu 2 (3điểm
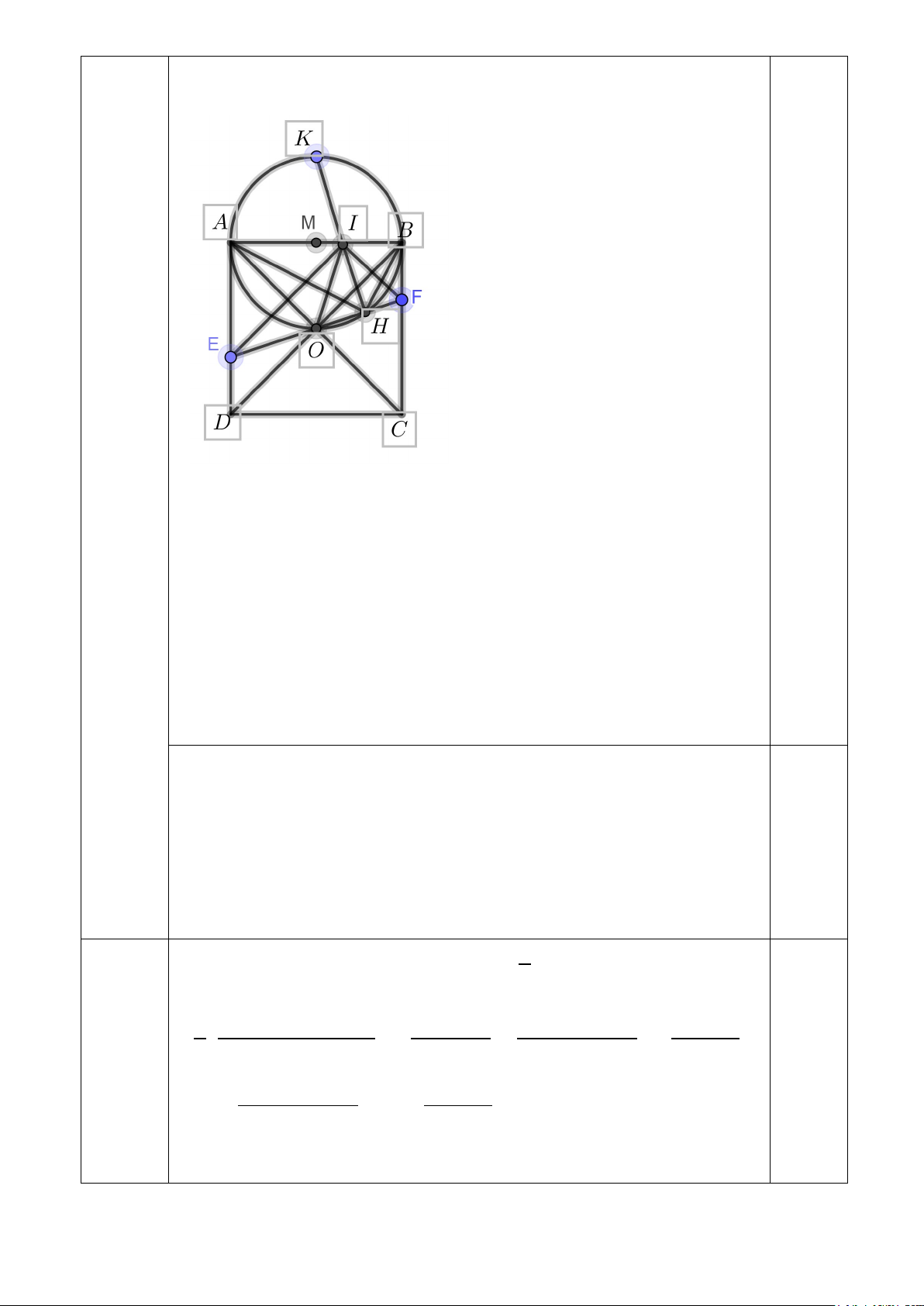
a) Dễ dàng chứng minh được E
∆ FI vuông ở I, và IO là trung tuyến thuộc
cạnh huyền EF, do đó OE = OI nên O nằm trên trung trực của EI
Mặt khác OA ⊥ EI nên OA là trung trực của EI. Nên A
∆ EI vuông cân tại A Suy ra 0
AIE = 45 . Tương tự 0 BIF = 45 . Vậy = + + 0 0 0 0
AIB AIE EIF BIF = 45 + 90 + 45 =180 suy ra I, , A B thẳng hàng
hay I ∈ AB (đpcm).
b) Ta có: AEHI và BFHI là các tứ giác nội tiếp. Suy ra 2 điểm = 0 = = 0 = ⇒ 0
AHI AEI 45 , IHB IFB 45
AHB = 90 . Vậy H ∈ đường tròn đường kính A . B (đpcm).
Gọi HI cắt đường tròn đường kính AB ở K , ta có = 0 AHK BHK = 45 nên
K là trung điểm cung
AB suy ra K cố định. (đpcm).
Câu 3 Theo BĐT AM-GM: ( a 1 điểm
− b)(b + )(b + ) 1 2 3
3 = (4a − 2b)(b + 3)(b + 3) 1điểm 2 3
1 4a − 2b + b + 3+ b + 3 4(2a + 3)3 3 64 6 ≤ = ⇒ ≥ 2. 2 3 27
(2a −b)(b +3)2 (2a +3)3 3 64 6 ⇒ 2a + ≥ 2 a + . (1) (2a b)(b 3)2 (2a 3)3 − + + Theo BĐT AM-GM ta có 3 3
2a + 3 2a + 3 2a + 3 6 6 3 5 + + + ≥ 4 ⇒ a + ≥ 4 − = (2) 6 6 6 (2a +3)3 (2a +3)3 2 2
Từ (1) và (2) suy ra đpcm. Dấu đẳng thức xảy ra khi 3 a = ,b =1. 2
Câu 4 a) Chia tập X thành các cặp (1,2),(3,4),...,(2019,2020). Có tất cả 1010 cặp 1 điểm
2điểm và 1011 phần tử nên theo nguyên tắc Dỉichlet, tồn tại hai phần tử thuộc cùng
một cặp. Hai phần tử này nguyên tố cùng nhau. (đpcm)
b) Xây dựng dãy (x ) : x =1, x =
− Ta chứng minh (x là dãy số 1 điểm n ) + 5 nx n n 1. 1 1
nguyên dương tăng và mọi số hạng của dãy đều thỏa mãn đk bài toán.
+ Thật vậy (x là dãy số nguyên dương. Áp dụng BĐT Becnuli ta có n ) x = − ≥ + − = >
Vậy (x là dãy số tăng. (1) n ) + 5 nx x x x n 1 1 4. n 1 4 1 n n
+ Dùng quy nạp chứng minh 5 nx −1x (*) n Với n=1, ta có 1
5x −1x (đúng) 1
Giả sử (*) đúng đến n, tức là 5 nx −1x ⇒ x = − = ∈ + 5 nx k x k n n 1 . n,( * 1 ) Ta có nx 1 5 + −1 = 5 n
kx −1(5 nx − ) n x 1
1 ⇒ 5 + −1x Theo nguyên lí quy nạp suy ra n+ . 1 n x * 5 −1x n ∀ ∈ n , (2).
Từ (1) và (2) suy ra đpcm. Câu 5 a) ta có 2
ax + bx + c = 0 ( ) 2
1 ,ax + bx + c = 0
2 Nhân hai vế của (1) 1 điểm 1 1 2 2 ( )
2điểm với n 2
x − và nhân hai vế của (2) với n 2
x − rồi cộng theo vế ta đc đpcm. 1 2
b) Ta có 1± 3 là nghiệm của PT 2
x − 2x − 2 = 0 nên 1 điểm S − S − = = = ⇒ = + = ⇒ = Vậy − S − S S S S S n 2 n 2 n 0,S 2, 2 2 2 8,... 3104. 1 2 0 1 2 1 0 8 A=31044. 2
Document Outline
- Toan 10 chuyen _De
- Toan 10 chuyen_DA




