Đề kiểm tra cuối học kỳ 2 Toán 10 năm 2021 – 2022 sở GD&ĐT Bắc Ninh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ II BẮC NINH NĂM HỌC 2021 - 2022 Môn: Toán - Lớp 10 (Đề có 02 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm) 2006
Câu 1. Hàm số y có tập xác định là x 10 A. 10; . B. \ 10 . C. 10; . D. 0; .
Câu 2. Cho phương trình 2 x 6x 2m 1
0 với m là tham số. Tìm tất cả các giá trị của m để
phương trình đã cho có nghiệm. 1 A. m 5. B. m 5. C. m 4 . D. m . 2
Câu 3. Kết quả bài kiểm tra cuối học kì 2 môn Toán của một lớp 10 ở một trường Trung học Phổ
thông được ghi lại trong bảng dưới đây. Điểm thi 3 4 5 6 7 8 9 10 Cộng Tần số 1 1 2 7 12 14 2 1 40
Độ lệch chuẩn (làm tròn đến hàng phần trăm) của mẫu số liệu trên bằng A. 2, 29 . B. 0, 21. C. 1, 77 . D. 1, 33 .
Câu 4. Trong mặt phẳng với hệ tọa độ Oxy , đường thẳng Ox có phương trình là x 0 x t x 0 x t A. . B. t . C. t . D. t . y 0 y t y t y 0
Câu 5. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A 3; 0 , B 0; 6 . Đường thẳng AB có phương trình là x y x y A. 3x 6y 0 . B. 3x 6y 1. C. 1. D. 0 . 3 6 3 6 2 2 x y
Câu 6. Trong mặt phẳng với hệ tọa độ Oxy , cho elip E :
1. Điểm nào sau đây không 9 4 thuộc elip E ? A. A 3; 0 . B. B 3; 0 .
C. C 0; 4 . D. D 0; 2 . x 3 2t
Câu 7. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d : t . Một vectơ y 4 5t
chỉ phương của đường thẳng d là A. u 3; 4 . B. u 2;5 . C. u 5; 2 . D. u 2;5 . 1 2 3 4 2 2
Câu 8. Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn C : x 3 y 5 36 . Tâm
và bán kính của đường tròn C lần lượt là
A. I 3; 5 , R 6 . B. I 3;5 , R
6 . C. I 3; 5 , R 36. D.I 3;5 ,R 36. Trang 1/2
Câu 9. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d đi qua điểm M 1; 1 và có một 0
vectơ pháp tuyến là n
3; 4 . Phương trình tổng quát của đường thẳng d là A. 3x 4y 7 0 . B. 3x 4y 1 0 . C. 4x 3y 1 0 . D. x y 7 0 .
Câu 10. Khẳng định nào sau đây đúng với mọi x ? A. 2 2 sin x cos x 1. B. 2 2 sin x cos x 0 . C. sin x cosx 1. D. 2 2 sin x cos x 1.
Câu 11. Khẳng định nào sau đây đúng với mọi u, v ? u v u v u v u v A. cos u cos v 2 cos cos . B. cos u cos v 2 sin sin . 2 2 2 2 u v u v u v v u C. sin u sin v 2 sin cos . D. sin u sin v 2 cos sin . 2 2 2 2 Câu 12. Cho
0 . Khẳng định nào sau đây sai? 2 A. sin 0. B. cos 0 . C. tan 0. D. cot 0.
II. TỰ LUẬN (7,0 điểm)
Câu 1. (2,0 điểm)
Giải các bất phương trình sau đây. a) 5x 6 9 . b) x x 8 7 0. c) 2 2x x 1 x 5 .
Câu 2. (2,0 điểm) 1 Cho cos với 0; . 3 2 a) Tính sin , tan , cot và sin 2 . 1
b) Tính giá trị của biểu thức 4 4 P sin cos cos . 4 4 2
Câu 3. (2,5 điểm)
Trong mặt phẳng với hệ tọa độ O ,
xy cho tam giác ABC với (
A 1;1), B(0;2), C(3;1).
a) Tìm tọa độ điểm M sao cho B là trung điểm của đoạn thẳng AM .
b) Viết phương trình đường tròn ngoại tiếp tam giác ABC .
c) Viết phương trình đường thẳng d sao cho khoảng cách từ điểm A tới d bằng 8 , khoảng
cách từ điểm B tới d bằng 2 .
Câu 4. (0,5 điểm)
Cho tam giác ABC có BC a , CA b , AB c thỏa mãn a b c 6 . Tìm giá
trị lớn nhất của biểu thức 1 1 1 F . a 16 b 16 c 16 ===== Hết ===== Trang 2/2
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
KIỂM TRA CUỐI HỌC KỲ 2 ¯¯¯¯¯¯¯¯¯¯
NĂM HỌC 2021 – 2022 (HDC có 04 trang)
Môn: Toán – Lớp 10
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
I. TRẮC NGHIỆM (3,0 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C B D D C C D B A A A B
II. TỰ LUẬN (7,0 điểm) Câu
Lời giải sơ lược Điểm 1. (2,0 điểm) a) Ta có 5x 6 9 5x 15 x 3. 0,5
Vậy bất phương trình có nghiệm x 3. b) Ta có 2 x x 8 7 0 x 8x 7 0 7 x 1. 0,5
Vậy bất phương trình có nghiệm 7 x 1. c) Giải bất phương trình 2 2x x 1 x 5. x 1 2 2x x 1 0 Trườ 1 ng hợp 1: x x 5 . x 5 0 2 x 5 Trường hợp 2: 0,75 x 5 x 5 0 x 5 5 x 2 x 13 2 2 . 2 2x x 1 x 5 x 11x 26 0 x 13 x 2
Lưu ý: Nếu học sinh chỉ giải quyết được trọn vẹn 1 trong 2 trường hợp trên thì
cho 0,5 điểm trong tổng số 0,75 điểm. x 2
Kết hợp hai trường hợp ta được nghiệm của bất phương trình đã cho là . x 13 0,25 2. (2,0 điểm) a) 2 1 1 2 2 Vì cos và 0; nên 2 sin 1 cos 1 . 0,25 3 2 3 3 sin 2 2 1 tan : 2 2. 0,25 cos 3 3 cos 1 2 2 2 cot : . 0,25 sin 3 3 4 2 2 1 4 2 sin 2 2 sin cos 2. . . 0,25 3 3 9 b) 1 4 4 P sin cos cos 4 4 2 Trang 3/2 2 1 2 2 2 2 sin cos 2 sin cos cos 0,25 4 4 4 4 2 1 1 2 1 sin cos 0,25 2 2 2 1 1 cos 1 1 . cos 0,25 2 2 2 3 3 cos 1. 0,25 4 3. (2,5 điểm) a)
Điểm B là trung điểm của đoạn thẳng AM nên x x 2x x 2x x x 2.0 1 1 A M B M B A . Do đó M . 0,5 Vậy M 1; 3 . y y 2y y 2y y y 2.2 1 3 A M B M B A M b) Gọi 2 2 T : x y 2ax 2by c
0 là đường tròn ngoại tiếp tam giác ABC , ở đó 0,25 a, ,
b c là các hằng số thoả mãn 2 2 a b c 0. Ta có 2 2 1 1 2a. 1 2 .1 b c 0 2 2 0 2 2a.0 2 .2 b c 0 0,25 2 2 3 1 2a.3 2 .1 b c 0 2a 2b c 2 a 1 4b c 4 b 0 . 0,25 6a 2b c 10 c 4 Vậy 2 2 T : x y 2x 4 0. 0,25 c) Cách 1: Vì d , A d 8 2 2, d , B d
2 nên đường thẳng AB và đường d
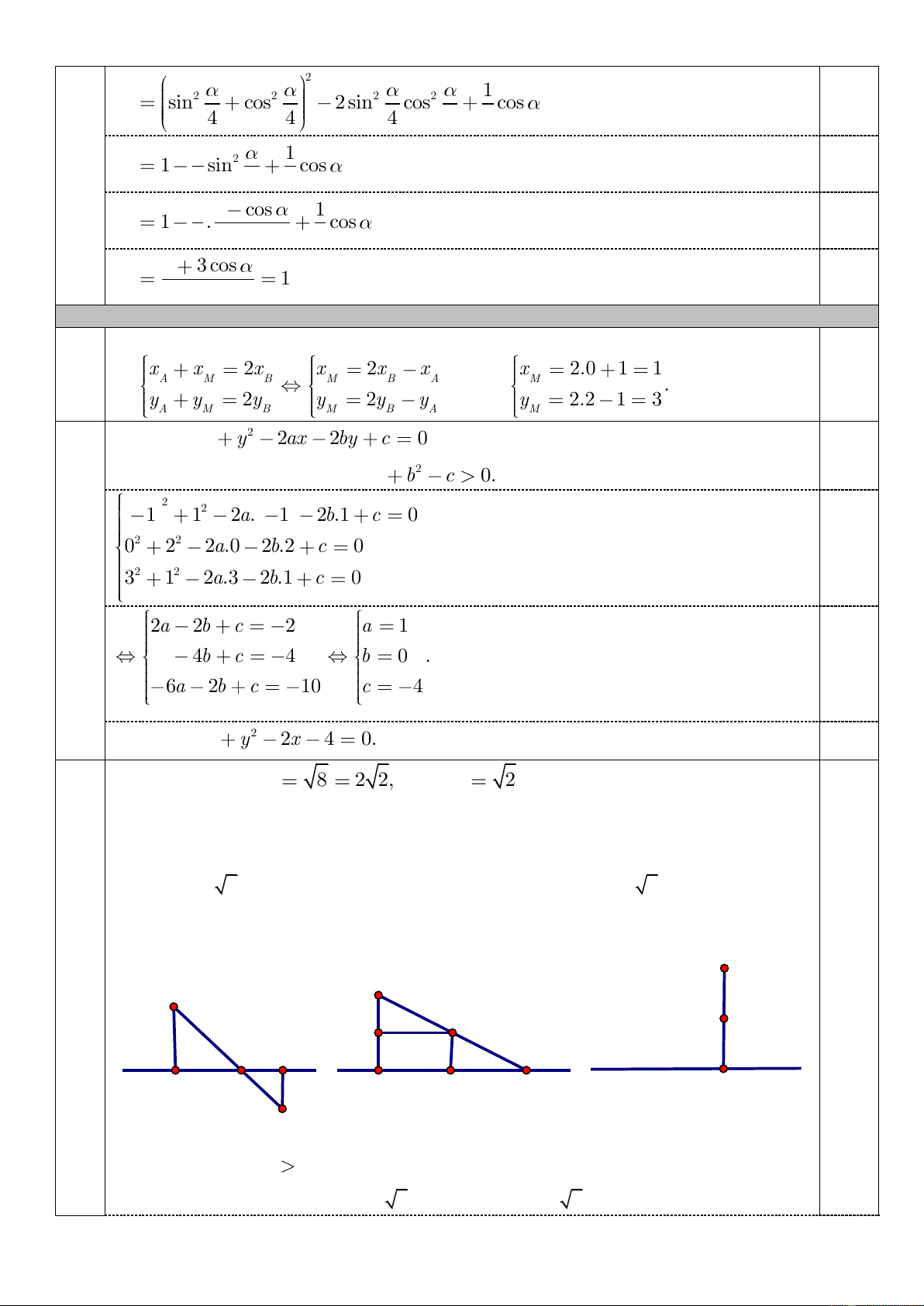
thẳng cắt nhau. Gọi N là giao điểm của AB và d , gọi H , K lần lượt là hình chiếu
vuông góc của A , B trên d , gọi E là hình chiếu vuông góc của B trên đường thẳng
AH . Nếu A , B nằm khác phía so với d thì
2  AB  AN  NB  AH  BK  d  , A d   d  ,
B d   3 2, vô lí.
Do đó A , B nằm cùng phía so với d . A A A 0,75 B B d E K d d N H H K N M B Lúc này, do d , A d d ,
B d nên điểm E thuộc đoạn thẳng AH. Ta có EH  BK 
2, AE  AH  EH  2  AB, Trang 4/2
dẫn tới E là trung điểm của AH , E trùng với B, các điểm H , K trùng với N. Mặt
khác, lại có B là trung điểm của AM nên suy ra M trùng với N. Như vậy, đường
thẳng d đi qua điểm M và vuông góc với AB .
Đường thẳng d đi qua điểm M 1; 3 và nhận AB  1 
;1 làm một vectơ pháp tuyến,
nên có phương trình là 1.x   1 1. y  
3  0  x  y  4  0. 0,25 Vậy d : x y 4 0 .
Cách 2: Gọi phương trình của đường thẳng d là ax by c 0 , với a, , b c là các hằng số thoả mãn 2 2 a b 0. Vì d , A d 8 2 2, d , B d 2 nên a b c 2 2 (0,25) 2 2 2 2 a b c 2 2. a b a b c 2 2b c a b . 2 2 2 2 2b c 2b c 2. a b 2b c 2. a b 2 2 2 a b Trường hợp 1: a b c 4b 2c a 3b c a 3b c 2 2 2 2 2 2 2 2 2b c 2. a b a b 2. a b a 2ab b 2a 2b a 3b c b a 2 . a b 0 c 4a Chọn a 1 thì b 1,c
4 , ta được d : x y 4 0 . Trường hợp 2: (0,75) a b c 4b 2c 3c a 5b 3c a 5b 2 2 2 2 2 2 2 2 2b c 2. a b a b 3 2. a b a 2ab b 18a 18b 3c a 5b 2 (hệ này vô nghiệm). 2 2 16a 16b a b 0 Vậy d : x y 4 0 .
Lưu ý: Nếu học sinh chỉ giải quyết được trọn vẹn 1 trong 2 trường hợp trên thì cho
0,5 điểm trong tổng số 0,75 điểm. 4. (0,5 điểm)
Do a , b , c là độ dài ba cạnh của một tam giác thỏa mãn a b c 6 nên a b a b c 6 a b c 2 c c 3. 2 Suy ra 3 c c 2 0 3 c c 4 c 4 0 0,25 7c c c 12 16 c 0 7c c c 112 16 c 100 c 16 7 c 100 Trang 5/2 1 7 c 1 . c 16 100 Dấu “=” ở  
1 xảy ra khi c  2 hay c  4. Tương tự ta có 1 7 a 1 7 b 2 , 3 . a 16 100 b 16 100
Dấu “=” ở 2,3 lần lượt xảy ra khi a  4,b  4. Từ  
1 , 2,3 và a b c 6 suy ra 0,25 1 1 1 7 a 7 b 7 c 3 F . a 16 b 16 c 16 100 100 100 20 3 Đẳng thức F
xảy ra khi a  b  c  4. 20 3 Vậy max F
, đạt được khi a  b  c  4. 20 Trang 6/2