




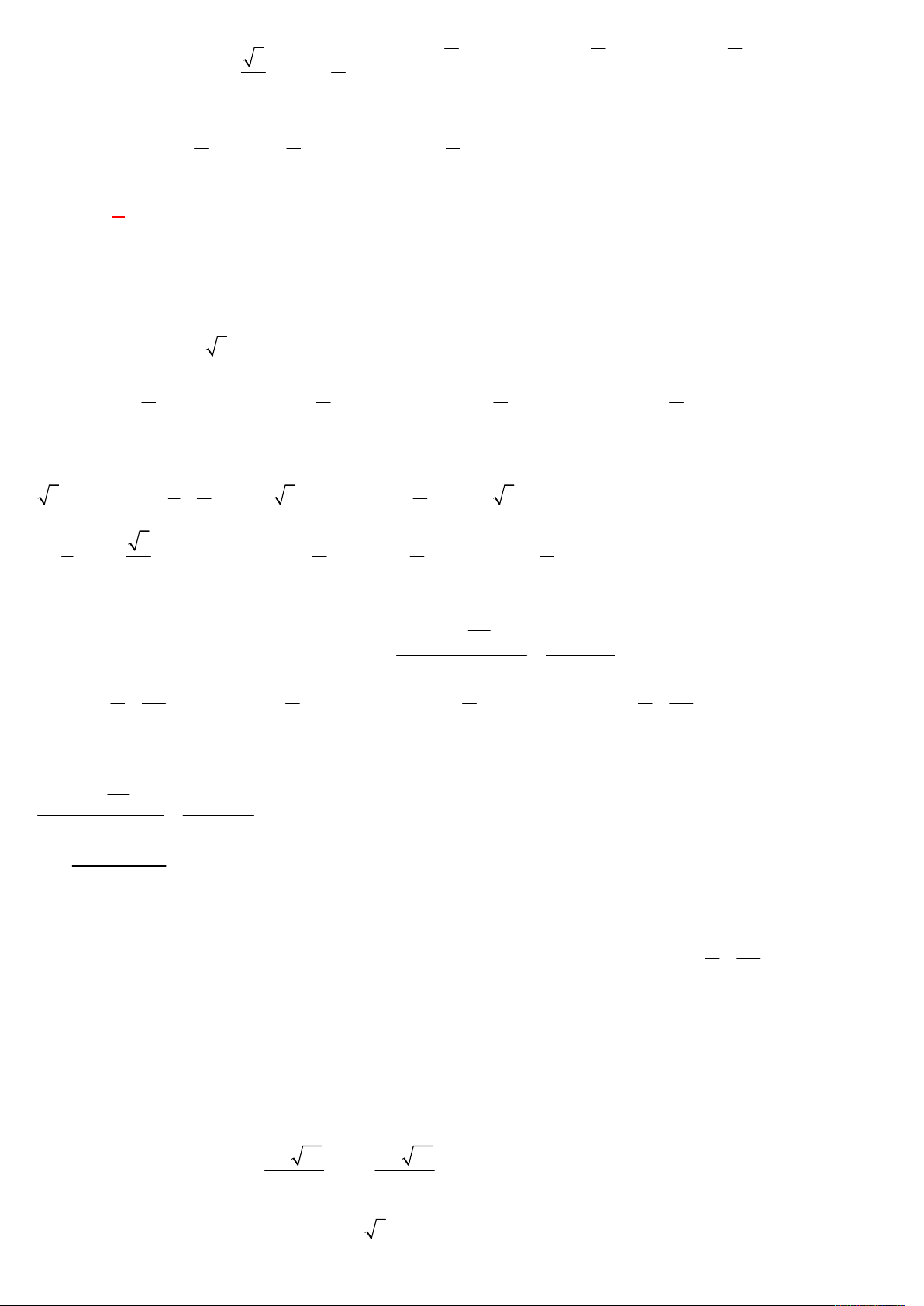

Preview text:
TRƯỜNG THPT AN LƯƠNG ĐÔNG KIỂM TRA ĐỊNH KỲ TỔ TOÁN
Môn: TOÁN - Năm học: 2019 - 2020 §Ò CHÝNH THøC
Thời gian: 45 phút (không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (8,0 ĐIỂM)
Câu 1: Phương trình sin 2x 3cos x 0 có bao nhiêu nghiệm trong khoảng 0; A. 0 . B. 1. C. 2 . D. 3 . x
Câu 2: Gọi X là tập nghiệm của phương trình cos 15 sin x
. Mệnh đề nào dưới đây đúng? 2 A. 290 X . B. 220 X . C. 240 X . D. 200 X . 2
Câu 3: Nghiệm của phương trình cos x là 4 2 x k 2 x k x k x k2 A. k . B. k . C. k . D. k x k x k x k 2
x k2 2 2 2 2
Câu 4: Tìm tập xác định D của hàm số y tan 2x :
A. D \ k2 | k .
B. D \ k | k . 4 2
C. D \ k | k .
D. D \ k | k . 4 4 2
Câu 5: Chọn phát biểu đúng:
A. Các hàm số y sin x , y cos x , y cot x đều là hàm số chẵn.
B. Các hàm số y sin x , y cos x , y cot x đều là hàm số lẻ.
C. Các hàm số y sin x , y cot x , y tan x đều là hàm số chẵn
D. Các hàm số y sin x , y cot x , y tan x đều là hàm số lẻ.
Câu 6: Tìm nghiệm của phương trình 2 2
sin 5x cos x sin x 0 π π π 2π π π x k x k x k2π x k2π 6 3 6 3 6 6 A. B. C. D. π π π 2π π π x k x k x k2π x k2π 14 7 14 7 14 14
Câu 7: Tìm góc ; ; ; để phương trình cos 2x 3 sin 2x 2 cos x 0 tương đương với phương 6 4 3 2
trình cos 2x cos x . A. . B. . C. . D. . 6 4 2 3 1
Câu 8: Tìm tập xác định D của hàm số y . sin x cos x
A. D \ k | k .
B. D \ k | k C. D \ k | k . D. D \ k2 | k 2 4 .
Câu 9: Tìm tập giá trị của hàm số y
3 sin x cos x 2 . A. 2; 3 .
B. 3 3; 3 1 . C. 4 ; 0 . D. 2 ; 0
Câu 10: Trong bốn hàm số: (1) y cos 2x , (2) y sin x ; (3) y tan 2x ; (4) y cot 4x có mấy hàm số tuần hoàn với chu kỳ ? A. 1. B. 0 . C. 2 . D. 3 .
Câu 11: Hàm số y sin x đồng biến trên khoảng nào sau đây? 5 7 9 11 7 7 9 A. ; . B. ; . C. ;3 . D. ; . 4 4 4 4 4 4 4
Câu 12: Gọi x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x 2 sin x cos x cos x 0 . Chọn khẳng định 0 đúng? 3 3 A. x ; 2 . B. x ; . C. x ; . D. x 0; . 0 0 0 0 2 2 2 2 3
Câu 13: Nghiệm của phương trình tan x
được biểu diễn trên đường y 3
tròn lượng giác ở hình bên là những điểm nào? B
A. Điểm F , điểm D . D C
B. Điểm C , điểm F .
C. Điểm C , điểm D , điểm E , điểm F . A' O A
D. Điểm E , điểm F . x
Câu 14: Số nghiệm chung của hai phương trình 2
4 cos x 3 0 và E F 3
2 sin x 1 0 trên khoảng ; là: 2 2 B' A. 4. B. 1. C. 2. D. 3. 3
Câu 15: Phương trình sin 2x
có hai công thức nghiệm dạng k , k k với , thuộc 2 khoảng ;
. Khi đó, bằng 2 2 A. . B. . C. . D. . 3 2 2
Câu 16: Tìm điều kiện của tham số m để phương trình 3sin x m cos x 5 vô nghiệm A. m 4 ; 4 . B. m ; 4
4; . C. m ; 4 .
D. m 4; . x Câu 16. Phương trình 2 3 cosx 2sin 1
tương đương với phương trình nào dưới đây 2 4 A. sin x 0 B. sin x 0 C. sin x 0 D. sin x 0 4 3 4 3 3 5 4 sin x 2 6 tan a
Câu 17: Tìm a để phương trình sau có nghiệm 2 sin x 1 tan a k k A. a . B. a k . C. a k 2 . D. a . 4 2 4 3 6 2
Câu 18: Có bao nhiêu số nguyên m để phương trình 2
2 cos x 2(m 1) sin x cos x 2m 3 có nghiệm thực. A. 11. B. 6. C. 5. D. 10.
Câu 19: Tập giá trị của hàm số y sin 2x 3 cos 2x 1 là đoạn ;
a b. Tính tổng T a b ? A. T 0 B. T 1 C. T 2 D. T 1 s inx
Câu 20: Gọi S là tổng các nghiệm của phương trình
0 trên đoạn 0; 2017 .Tính S. cos x 1 A. S 2035153 B. S 1001000 C. S 1017072 D. S 200200
II. PHẦN TỰ LUẬN (2,0 ĐIỂM)
Giải tự luận các bài 15 và bài 18.
Câu 1: Phương trình sin 2x 3cos x 0 có bao nhiêu nghiệm trong khoảng 0; A. 0 . B. 1. C. 2 . D. 3 . Lời giải. Chọn B
sin 2x 3cos x 0 2 sin .
x cos x 3cos x 0 cos .
x 2sin x 3 0
cos x 0 x k k 2 3 sin x
loai vì sin x 1 ;1 2
Theo đề: x 0; k 0 x . 2 x
Câu 2: Gọi X là tập nghiệm của phương trình cos 15 sin x
. Mệnh đề nào dưới đây đúng? 2 A. 290 X . B. 220 X . C. 240 X . D. 200 X . Lời giải Chọn A x x Xét phương trình: cos
15 sin x cos 15 cos 90 x 2 2 x 3x
15 90 x k360 75 k360 x 50 120 2 2 k , k x x
x 210 k720 15 90 x k360 105 k360 2 2
Vậy 290 50 2.120 X . 2
Câu 3: Nghiệm của phương trình cos x là 4 2 x k 2 x k A. k . B. k . x k x k 2 2 x k x k 2 C. k . D. k . x k 2 x k 2 2 2 Lời giải Chọn D x k 2 2 Phương trình cos x cos x cos k . 4 2 4 4 x k 2 2
Câu 4: Tìm tập xác định D của hàm số y tan 2x :
A. D \ k2 | k .
B. D \ k | k . 4 2
C. D \ k | k .
D. D \ k | k . 4 4 2 Giải: Chọn D
Hàm số xác định khi cos 2x 0 2x
k x k k . 2 4 2
Tập xác định của hàm số là: D \ k | k . 4 2
Câu 5: Chọn phát biểu đúng:
A. Các hàm số y sin x , y cos x , y cot x đều là hàm số chẵn.
B. Các hàm số y sin x , y cos x , y cot x đều là hàm số lẻ.
C. Các hàm số y sin x , y cot x , y tan x đều là hàm số chẵn
D. Các hàm số y sin x , y cot x , y tan x đều là hàm số lẻ. Giải: Chọn D
Hàm số y cos x là hàm số chẵn, hàm số y sin x , y cot x , y tan x là các hàm số lẻ.
Câu 6: Tìm nghiệm của phương trình 2 2
sin 5x cos x sin x 0 π π π 2π π π x k x k x k2π x k2π 6 3 6 3 6 6 A. B. C. D. π π π 2π π π x k x k x k2π x k2π 14 7 14 7 14 14 Đáp án là B 2 2
sin 5x cos x sin x 0 sin 5x cos 2x 0 sin 5x sin 2 x 2 k 2 5x 2 x k 2 x 2 14 7 k 2 k 2
5x 2x k2 x 2 2 3 6 3
Câu 7: Tìm góc ; ; ; để phương trình cos 2x 3 sin 2x 2 cos x 0 tương đương với phương 6 4 3 2
trình cos 2x cos x . A. . B. . C. . D. . 6 4 2 3 Lời giải Chọn D k 2
2x x k 2 x
cos 2x cos x 3 3
2x x k 2
x k 2 1 3
cos 2x 3 sin 2x 2 cos x 0 cos 2x
sin 2x cos x 2 2 x k 2 3 cos 2x cos x 3 k 2 x 9 3 3 9
Để hai phương trình tương đương cần có . 3 3 1
Câu 8: Tìm tập xác định D của hàm số y . sin x cos x
A. D \ k | k
. B. D \ k | k . 2
C. D \ k | k .
D. D \ k 2 | k 4 . Lời giải Chọn C
Hàm số đã cho xác định khi và chỉ khi
sin x cos x 0 sin x 0 x
k ,k . 4 4
Câu 9: Tìm tập giá trị của hàm số y
3 sin x cos x 2 . A. 2; 3 .
B. 3 3; 3 1 . C. 4 ; 0 . D. 2;0 Lời giải Chọn C
Xét y 3 sin x cos x 2 2 sin . x cos cos . x sin 2 2 sin x 2 6 6 6
Ta có 1 sin x 1 4 2sin x 2 0 4
y 0 với mọi x 6 6
Vậy tập giá trị của hàm số là 4 ; 0 .
Câu 10: Trong bốn hàm số: (1) y cos 2x , (2) y sin x ; (3) y tan 2x ; (4) y cot 4x có mấy hàm số tuần hoàn với chu kỳ ? A. 1. B. 0 . C. 2 . D. 3 . Lời giải Chọn A
Do hàm số y cos x tuần hoàn với chu kỳ 2 nên hàm số (1) y cos 2x tuần hoàn chu kỳ .
Hàm số (2) y sin x tuần hoàn với chu kỳ 2 .
Do hàm số y tan x tuần hoàn với chu kỳ nên hàm số (3) y tan 2x tuần hoàn chu kỳ . 2
Do hàm số y cot x tuần hoàn với chu kỳ nên hàm số (4) y cot 4x tuần hoàn chu kỳ . 4
Câu 11: Hàm số y sin x đồng biến trên khoảng nào sau đây? 5 7 9 11 7 7 9 A. ; . B. ; . C. ;3 . D. ; . 4 4 4 4 4 4 4 Lời giải Chọn D
Dựa vào định nghĩa đường tròn lượng giác ta thấy hàm số lượng giác cơ bản y sin x đồng biến ở góc
phần tư thứ nhất và góc phần tư thứ tư. 7 9 Dễ thấy khoảng ;
là phần thuộc góc phần tư thứ tư và thứ nhất nên hàm số đồng biến. 4 4
Câu 12: Gọi x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x 2 sin x cos x cos x 0 . Chọn khẳng định 0 đúng? 3 3 A. x ; 2 . B. x ; . C. x ; . D. x 0; . 0 0 0 0 2 2 2 2 Lời giải Chọn D
Ta thấy cos x 0 không thỏa phương trình. Chia hai vế phương trình cho 2
cos x 0 ta được: 2
3 tan x 2 tan x 1 0 tan x 1 x k 4 1
, k, l . tan x 1 3 x arctan l 3 1
Vậy nghiệm dương nhỏ nhất của phương trình là arctan 0; . 3 2 3
Câu 13: Nghiệm của phương trình tan x
được biểu diễn trên đường tròn lượng giác ở hình bên là những 3 điểm nào? y B D C A' O A x E F B'
A. Điểm F , điểm D .
B. Điểm C , điểm F .
C. Điểm C , điểm D , điểm E , điểm F .
D. Điểm E , điểm F . Lời giải: Chọn A 3 tan x x
k , k . 3 3 2
Với 0 x 2 x hoặc x . 3 3 3
Câu 14: Số nghiệm chung của hai phương trình 2
4 cos x 3 0 và 2 sin x 1 0 trên khoảng ; là: 2 2 A. 4. B. 1. C. 2. D. 3. Đáp án C x k 2 3 2 6
4cos x 3 0 osx= c 2 5 x k 2 6 x k 2 1 6
2sinx+1=0 sinx 2 7 x k 2 6
Vậy 2 pt trên có 2 họ nghiệm chung là: x k 2 6 5 7 x k 2 k 2 6 6 3
Câu 15: Phương trình sin 2x
có hai công thức nghiệm dạng k , k k với , thuộc 2 khoảng ;
. Khi đó, bằng 2 2 A. . B. . C. . D. . 3 2 2 Lời giải Chọn B 2x k 2 x k x k 3 3 6 6 Ta có: sin 2x sin . 2 3 4 2 2x k 2 x k
x k 3 3 3 Vậy và . Khi đó . 6 3 2
Câu 16: Tìm điều kiện của tham số m để phương trình 3sin x m cos x 5 vô nghiệm A. m 4 ; 4 . B. m ; 4 4; . C. m ; 4 .
D. m 4; . Lời giải Chọn A
Để phương trình đã cho vô nghiệm thì 2 2 2 3 m 5 2
m 16 4 m 4 . x Câu 16. Phương trình 2 3 cosx 2sin 1
tương đương với phương trình nào dưới đây 2 4 A. sin x 0 B. sin x 0 C. sin x 0 D. sin x 0 4 3 4 3 Đáp án B Ta có: x 2 3 cos x 2sin 1
3 cos x cos x
0 3 cos x sin x 0 2 4 2 1 3 sin x cos x 0 sin . x cos cos . x sin 0 sin x 0. 2 2 3 3 3 3 5 4 sin x 2 6 tan a
Câu 17: Tìm a để phương trình sau có nghiệm 2 sin x 1 tan a k k A. a . B. a k . C. a k 2 . D. a . 4 2 4 3 6 2 Đáp án A Ta có: 3 5 4.sin( x) 6 tan 2 2 s inx 1 tan 5 4( osx) c 3sin 2 s inx
3sin 2.s inx 4 cos x 5
Để phương trình có nghiệm => k 2 2 2 2 2
(3sin 2 ) 4 5 sin 2 1 sin 2 1 sin 2 1 os c 2 =0<=> = 4 2
Câu 18: Có bao nhiêu số nguyên m để phương trình 2
2 cos x 2(m 1) sin x cos x 2m 3 có nghiệm thực. A. 11. B. 6. C. 5. D. 10. Đáp án C
Phương trình tương đương với:
(1 cos 2x) (m 1) sin 2x 2m 3 (m 1) sin 2x cos 2x 2m 4. Phương trình có nghiệm: 9 39 9 39 2 2 2
(2m 4) (m 1) 1 m
m 1, 2,3, 4, 5 . 3 3
Có 5 số nguyên thoả mãn.
Câu 19: Tập giá trị của hàm số y sin 2x 3 cos 2x 1 là đoạn ;
a b. Tính tổng T a b ? A. T 0 B. T 1 C. T 2 D. T 1 Đáp án C
Ta có y sin 2x 3 cos 2x 1 2sin 2x 1 3 a 1 Vì 1 sin 2x
1 1 2 sin 2x 1 3
T a b 2. 3 3 b 3 s inx
Câu 20: Gọi S là tổng các nghiệm của phương trình
0 trên đoạn 0; 2017 .Tính S. cos x 1 A. S 2035153 B. S 1001000 C. S 1017072 D. S 200200 Đáp án C s inx cos x 1 0 cos x 1 Phương trình 0
cos x 1 x k 2 k . 2 cos x 1 s inx 0 1 os c x 0 2017
Mà x 0; 2017 x k2 0; 2017 0 k
suy ra k 0;1; 2; ...;1008 . Khi đó 2 u d 2
S 2 4 ... 2016 . Dễ thấy S là tổng của CSC với 1 n 1008. u 2016 n
n u u 1008. 2 2016 1 n Suy ra S
1008.1009 1017072 . 2 2




