Đề kiểm tra định kỳ Giải tích 12 chương 3 trường THPT Triệu Quang Phục – Hưng Yên

SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯNG YÊN
ĐỀ KIỂM TRA ĐỊNH KÌ
TRƯỜNG THPT TRIỆU QUANG PHỤC
MÔN GIẢI TÍCH LỚP 12- CHƯƠNG 3
Thời gian làm bài: 45 phút
Họ và tên học sinh :....................................................... Lớp : ................... Mã đề 838
I. Phần trắc nghiệm ( 20 câu – 8 điểm )
Câu 1. Tìm họ các nguyên hàm của hàm số f ( x) 1 = . 5x − 2 dx dx 1 A.
= 5ln 5x − 2 + C ∫ . B.
= − ln(5x − 2) + C ∫ . 5x − 2 5x − 2 2 dx dx 1 C.
= ln 5x − 2 + C ∫ . D.
= ln 5x − 2 + C ∫ . 5x − 2 5x − 2 5 1
Câu 2. Tìm họ các nguyên hàm của hàm số f ( x) = . 2 sin x A. f
∫ (x)dx = −cot x+C . B. f
∫ (x)dx = tan x+C . C. f
∫ (x)dx = −tan x+C . D. f
∫ (x)dx = cot x+C .
Câu 3. Tìm họ các nguyên hàm của hàm số f (x) = 2sin x . A. 2
2 sin xdx = sin x + C ∫ .
B. 2 sin xdx = 2 cos x + C ∫ .
C. 2 sin xdx = 2 − cos x + C ∫ .
D. 2 sin xdx = sin 2x + C ∫ . 2 2 2
Câu 4. Tính tích phân I = 2x x − 1dx ∫
bằng cách đặt u = x − 1 . Mệnh đề nào dưới đây đúng? 1 3 2 1 3 2
A. I = ∫ udu .
B. I = ∫ udu I 2 udu I udu 2 . C. = ∫ . D. = ∫ . 0 1 0 1
Câu 5. Xét hàm số F (x) là một nguyên hàm của hàm số f (x) trên [a;b]. Khẳng định nào sau đây luôn đúng? b b A.
f (x)dx = F (b) + F (a) ∫ .
B. F (x)dx = f (b) + f (a) ∫ . a a b b C.
f (x)dx = F (b) − F (a) ∫ .
D. F (x)dx = f (b) − f (a) ∫ . a a 4 1 Câu 6. Cho f
∫ (x)dx = 9 . Tính tích phân I = f (3x+ ∫ ) 1 dx . 1 0
A. I = 27 .
B. I = 3 .
C. I = 9 . D. I = 1. 1 1 1 Câu 7. Cho
f (x)dx = 1 ∫ và
g(x)dx = 2 − ∫
. Tính ∫ (1− f (x) + 3g(x)) . dx 2 − 2 − 2 − A. 24. B. 7. − C. 4. − D. 8. 1
Câu 8. Tính tích phân: = 3x I dx ∫ . 0 2 3 1 A. I = . B. I = .
C. I = 2 . D. I = . ln 3 ln 3 4 1/4 - Mã đề 838
Câu 9. Một vật thể trong không gian được giới hạn bởi hai mặt phẳng x = a, x = b . Một mặt phẳng
tùy ý vuông góc với trục Ox tại điểm x (a ≤ x ≤ b) cắt vật thể theo thiết diện là một hình vuông có đường chéo bằng 2
2 x +1 . Thể tích của vật thể bằng b b A. 2 2(x +1)dx ∫ . B. 2 2 x +1 . dx ∫ a a b b C. 2 2π (x +1)dx ∫ . D. 2 π 4(x +1)dx ∫ . a a 3
Câu 10. Cho F (x) là một nguyên hàm của hàm số ( ) x
f x = e + 2x thỏa mãn F (0) = . Tìm F (x) . 2 x 5 x 3 A. 2
F (x) = e + x + . B. 2
F (x) = e + x + . 2 2 x 1 x 1 C. 2
F (x) = e + x + . D. 2
F (x) = 2e + x − . 2 2
Câu 11. Thể tích vật thể tròn xoay tạo thành khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số π
y = cos x , đường thẳng y = 1, trục tung, đường thẳng x =
khi xoay quanh trục Ox bằng 2 2 π 2 3π 2 3π 2 π A. . B. − 2π . C. − + π . D. . 2 4 4 4
Câu 12. Xét hàm số f (x) có
f (x) = F (x) + C. ∫
Với a,b là các số thực và a ≠ 0, khẳng định nào sau đây luôn đúng? 1 A.
f (ax + b) =
F (ax + b) + C ∫ . B.
f (ax + b) = aF (ax + b) + C ∫ . a C.
f (ax + b) = F (ax + b) + C ∫ . D.
f (ax + b) = aF (x) + b + C ∫ . 3 3 2 Câu 13. Cho
f (x)dx = a,
f (x)dx = b ∫ ∫
. Khi đó f (x)dx ∫ bằng 0 2 0
A. a − b .
B. −a − b .
C. a + b .
D. b − a . 1 3 x 1 1 Câu 14. Biết dx = − ln 2 ∫ . Tính a . 2 x +1 2 a +1 0
A. a = 2 . B. a = 2 − .
C. a = 1. D. a = 0 .
Câu 15. Tìm nguyên hàm của hàm số f ( x) = cos 3x . sin 3x A. cos 3xdx = + C ∫ .
B. cos 3xdx = 3sin 3x + C ∫ . 3 sin 3x
C. cos 3xdx = − + C ∫ .
D. cos 3xdx = sin 3x + C ∫ . 3
Câu 16. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = x − x , trục hoành, các đường thẳng x = 2, − x = 1 bằng 1 1 1 1 A. 3
(x − x)dx . ∫ B. 3 (x − x) . dx ∫ C. 3 x − x . dx ∫ D. 3 x − x . dx ∫ 2 − 2 − 1 − 2 −
Câu 17. Họ các nguyên hàm của hàm số f (x) = sin x + cos x là 2/4 - Mã đề 838
A. sin 2x + C .
B. − cos x − sin x + C .
C. cos x + sin x + C .
D. sin x − cos x + C . π 2
Câu 18. Tính tích phân I = x sin xdx ∫ . 0 A. 3. B. 1. C. -1. D. 2. 1
Câu 19. Tìm I = dx ∫ . 2 4 − x 1 x − 2 1 x + 2 A. I = ln . B. I = ln . 4 x + 2 2 x − 2 1 x + 2 1 x − 2 C. I = ln . D. I = ln . 4 x − 2 2 x + 2
Câu 20. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2
x − 2x + 3 , trục Ox và các đường thẳng x = 1 − ; x = 2 bằng 1 A. 9 . B. . C. 17 . D. 7 . 3
II. Phần tự luận ( 3 câu – 2 điểm )
Câu 1. ( 0,5 điểm ) Tính = .ex I x dx ∫ .
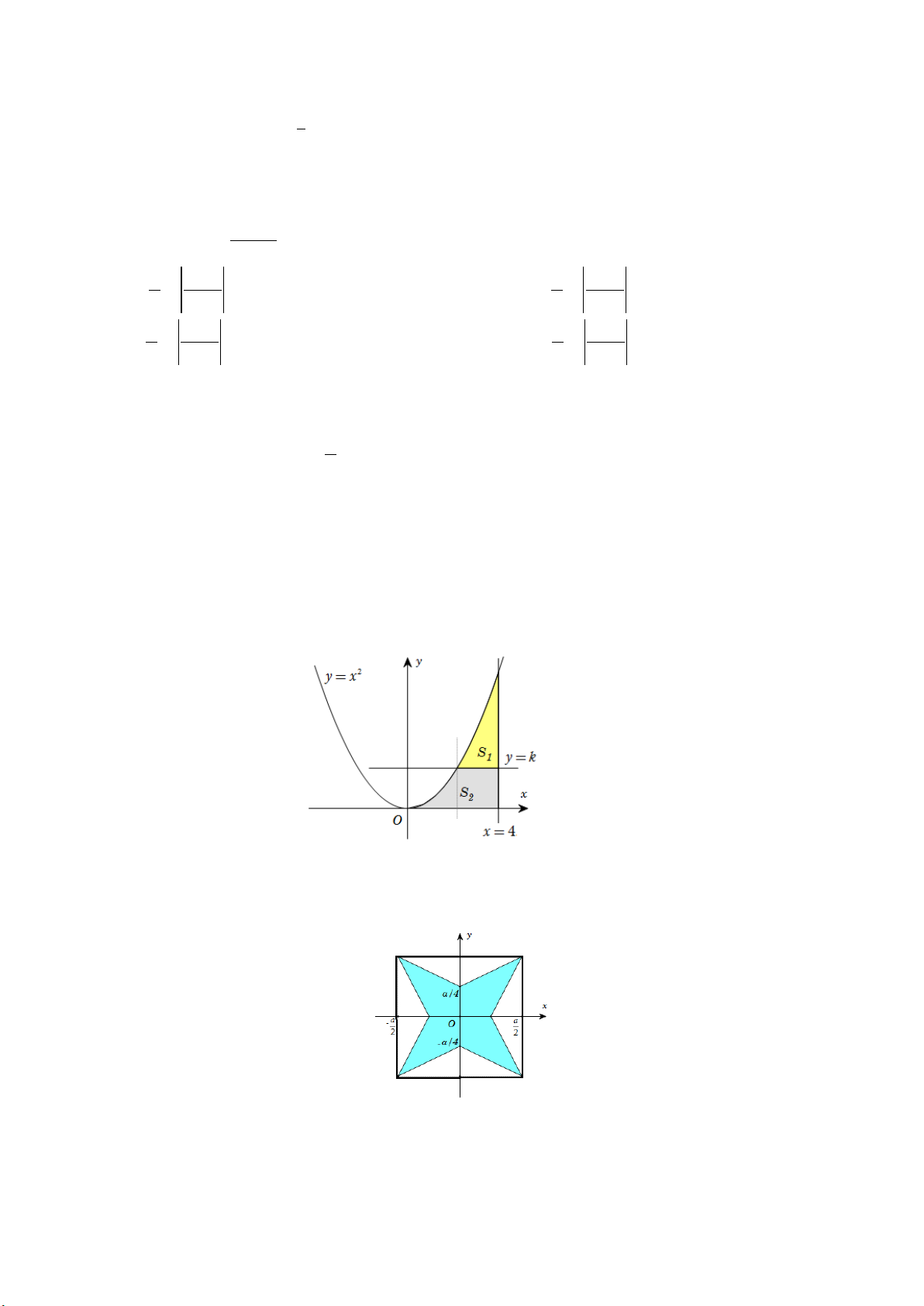
Câu 2. ( 0,5 điểm ) Cho hình phẳng H  giới hạn bởi các đường 2 y = x , y = 0, x = 0, x = 4. Đường thẳng y = k (
0 < k < 16) chia hình H  thành hai phần có diện tích S , S (hình vẽ). Tìm k để 1 2 S = S . 1 2
Câu 3. ( 1 điểm ) Bên trong hình vuông cạnh a , dựng hình sao bốn cánh đều như hình vẽ bên (các
kích thước cần thiết cho như ở trong hình). Tính thể tích V của khối tròn xoay sinh ra khi quay hình
sao đó quanh trục Ox .
……………………HẾT………………… 3/4 - Mã đề 838
I. TRẢ LỜI PHẦN TRẮC NGHIỆM. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
II. TRẢ LỜI PHẦN TỰ LUẬN.
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………............ 4/4 - Mã đề 838 SỞ GD&ĐT HƯNG YÊN ĐÁP ÁN
TRƯỜNG THPT TRIỆU QUANG PHỤC
MÔN TOÁN – Khối 12
Thời gian làm bài : 45 phút
I. Phần đáp án câu trắc nghiệm:
Tổng câu trắc nghiệm: 20. 838 839 840 841 1 D B D B 2 A A D A 3 C C B C 4 A D B D 5 C B C A 6 B B C C 7 C A C D 8 A B C D 9 A A A B 10 C D A B 11 D D C C 12 A B D B 13 A B B D 14 C B C A 15 A C C B 16 D A D C 17 D C A D 18 B C A A 19 C B B A 20 A A A C
II. Phần đáp án tự luận. 1 Câu Đáp án Thang điểm Câu 1  =  = Đặt u x du dx 0,25đ  ⇒  x x ( 0,5đ ) dv = e dx v = e Khi đó = .ex = . x x − = . x x I x dx x e
e dx x e − e + C ∫ ∫ 0,25đ Câu 2
. Phương trình hoành độ giao điểm: 2 x  k 
 x  k . Ta có: 0,25đ 4 3 4 x 64 ( 0,5đ ) ● 2 S S  x dx   . 1 2  3 3 0 0 4 4 3 ●   S    x 2   k k 64 2
x  k dx   kx  4k   . 1   3  3 3 k k Theo giả thiết 1 2k k 64 32 S  S  S 
S S  4k    0,25đ 1 2 1  1 2  2 3 3 3
t k 0t4 3 2
 2k k 12k  32  0 2t 12t 32  0  t  2   k  4.
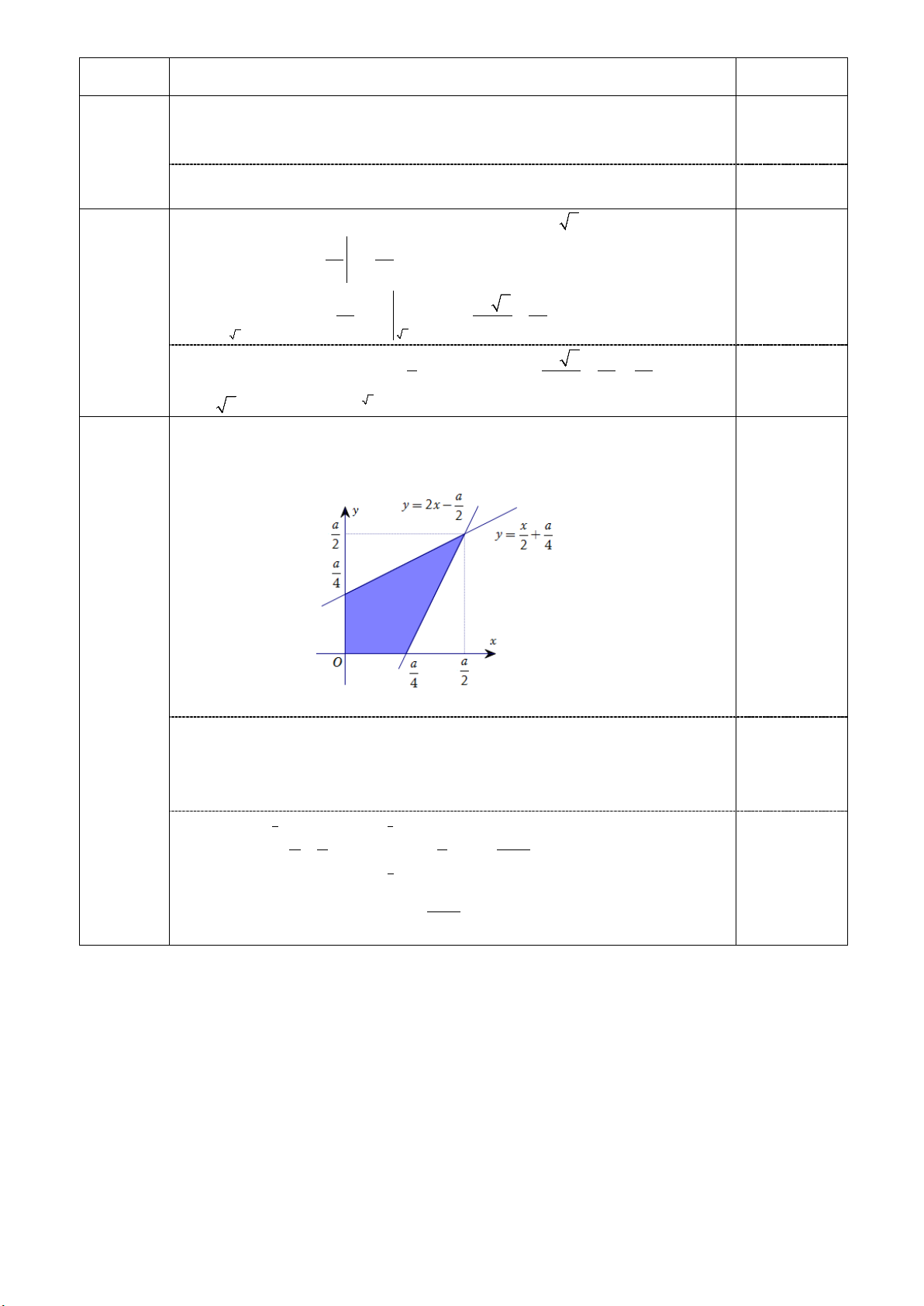
Do hình sao có tính đối xứng nên ta quay theo trục thẳng đứng hay nằm Câu 3 0,25đ
ngang đều cho thể tích như nhau. ( 1đ )
Chọn hệ trục tọa độ như hình vẽ. 0,25đ Gọi
V là thể tích khối tròn xoay cần tính.
Gọi V1 là thể tích khối tròn xoay khi quay hình phẳng được tô màu trong
hình bên quanh trục hoành. Khi đó V  2V .1 a a 2 2 2 2 3  0,5đ x a   a  5a
Ta có V    
    dx      2x    dx  . 1 2 4  2 96 0 a 4 3
Suy ra thể tích cần tính 5a V  2V  . 1 48
--------------HẾT-------------- 2
Document Outline

• de 838
• ĐÁP ÁN