Đề kiểm tra Giải tích 12 chương 2 năm 2019 – 2020 trường Nguyễn Trãi – Đà Nẵng

TRƯỜNG THPT NGUYỄN TRÃI
KIỂM TRA 1 TIẾT NĂM HỌC 2019 – 2020 TỔ TOÁN - TIN Môn: Toán - Lớp 12 - Chương II U
Thời gian làm bài: 45 phút (không kể thời gian phát đề) ĐỀ GỐC
Họ và tên thí sinh: …………………………………………. Lớp: ……… SBD: ..……… Câu 1. Với ;
a b là các số thực dương và ;
m n là các số nguyên, mệnh đề nào sau đây sai? a n
A. log a − log b = log . B. ( . ) n a b = a . n b . b C. m. n m n a a a + = .
D. log a + log b = log .
a log b . Lời giải Chọn D
Câu 2. Cho a là số thực dương, ,
m n tùy ý. Phát biểu nào sau đây là phát biểu sai? m m a  a  m a − n A. m n m n a a a + + = . B. =   . C. m n = a . D. ( m ) m.n a = a . m b  b  n a Lời giải Chọn A m n m n a a a + + =
lũy thừa không có tính chất này.
Câu 3. Biểu thức a a (
, a > 0) được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 3 3 1 2 A. 4 a . B. 2 a . C. 2 a . D. 3 a . Lời giải Chọn A 1 3 3 Ta có: 2 2 4 a . a = . a a = a = a .
Câu 4. Tìm tập xác định của hàm số y = log x +10 . A. (0; +∞) . B. ( 1 − 0;+∞) . C.  . D. ∅ . Lời giải Chọn A
Hàm số đã cho xác định x > 0 .
Câu 5. Tìm tập xác định D với của hàm số y = ( x + x − )e 2 2 3 . A. D = ( ; −∞ 3 − ) ∪(1;+∞).
B. D = (0; +∞) . C. D =  \ { 3 − ; } 1 .
D. D =  . Lời giải Chọn A  > Điều kiện: x 1 2
x + 2x − 3 > 0 ⇔  x < 3 − Vậy D = ( ; −∞ 3 − ) ∪(1;+∞).
Câu 6. So sánh hai số 2019 a = π
; log b = 2019 . 3
A. a < b .
B. a = b .
C. a > b .
D. không so sánh được.
Trang 1/6 - Mã đề thi 114 - https://toanmath.com/ Lời giải Chọn C U 2019 2019 a = π ; b = 3 Ta có:  ⇒ a > . b π  > 3 x− 1
Câu 7. Giải phương trình 4 π = π .
A. x = 5 .
B. x = 3 .
C. x = 4 − π . D. x = 5 − Lời giải Chọn B x− 1 Ta có: 4 π = ⇔ − = − ⇔ = π x 4 1 x 3 .
Câu 8. Tập nghiệm của phương trình log 1− x = 0 . 2 ( ) A. S = { } 2 . B. S = { } 0 .
C. S =  .
D. S = ∅ . Lời giải Chọn B
Điều kiện: x <1.
Phương trình tương đương với 1− x =1 ⇔ x = 0 .
Câu 9. Tập nghiệm của phương trình log x = log ( 2
x − x là: 2 2 ) A. S = { } 2 . B. S = { } 0 . C. S = {0; } 2 . D. S = {1; } 2 Lời giải Chọn A
Điều kiện x >1.
Với điều kiện trên ta có: x = log x = log ( 2 x − x 2
⇔ x = x − x 2 ⇔ x − 2x = 0 0 ⇔ . 2 2 )  x = 2
Đối chiếu điều kiện phương trình có tập nghiệm là S = { } 2 .
Câu 10. Bất phương trình 2x > 4 có tập nghiệm là:
A. T = (2; +∞) .
B. T = (0; 2) . C. T = ( ; −∞ 2) .
D. T = ∅ . Lời giải Chọn A x x 2
2 > 4 ⇔ 2 > 2 ⇔ x > 2 .
Vậy tập nghiệm của bất phương trình là: T = (2;+∞) . π
Câu 11. Cho hàm số y = x . Tính y′′( ) 1 . A. y′′( ) 2 1 = ln π . B. y′′( ) 1 = π ln π . C. y′′( ) 1 = 0 . D. y′′( ) 1 = π (π − ) 1 Hướng dẫn giải Chọn D π − π − Ta có 1 y′ = π x
⇒ y′′ = π (π − ) 2 1 x do đó y′′( ) 1 = π (π − ) 1 .
Câu 12. Tập nghiệm của phương trình 4 log x = log x là: 4 2 2 A.  . B. ∅ . C. { } 4 . D. (0; +∞) . Lời giải Chọn D
Trang 2/6 - Mã đề thi GỐC - https://toanmath.com/
Điều kiện xác định: x > 0 . Ta có: 4 log x = log
x ⇔ 4 log x = 4 log x đúng với mọi x > 0 4 2 2 2 2 . 3 1 + 2− 3 a .a
Câu 13. Rút gọn biểu thức P =
, với a > 0 . 2 −2 2 +2 (a ) A. 5 P = a . B. 4 P = a .
C. P = a . D. 3 P = a . Lời giải Chọn A 3 1 + 2− 3 3 1 + +2− 3 3 a .a a a + Ta có: 3 2 5 P = = = = = − + ( − )( + ) a a . 2 2 2 2 2 2 2 2 2 − (a ) a a
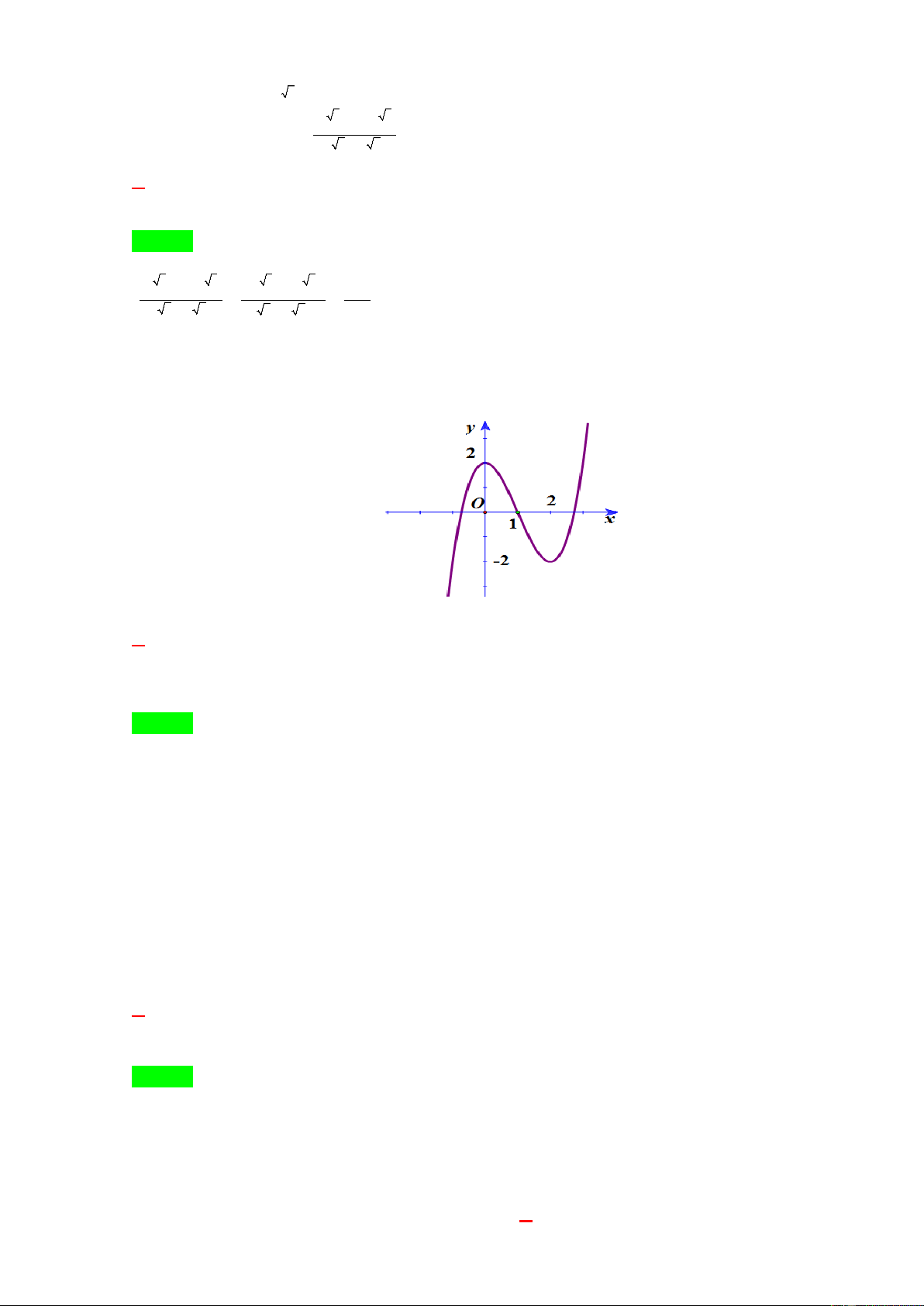
Câu 14. Cho hàm số y = f ( x) liên tục trên  . Đồ thị hàm số y = f ( x) như hình vẽ. Tìm giá trị của tham
số m để đồ thị hàm số y = f (x) cắt đường thẳng 2m y =
tại hai điểm phân biệt A. m ∈ (0; ] 1 . B. m ∈[ 1 − ;0].
C. m > 1. D. m < 1 − . Lời giải Chọn A
Ta có phương trình hoành độ giao điểm ( ) 2m f x = .
Dựa vào đồ thị ta có để đồ thị hàm số y = f (x) cắt đường thẳng 2m y =
tại hai điểm phân biệt khi
2m = 2 ⇔ m = 1.
Câu 15. Phương trình 2 log x − log
8x + 3 = 0 tương đương với phương trình nào sau đây? 2 2 ( ) A. 2
log x + log x = 0 . B. 2
log x − log x − 6 = 0 . 2 2 2 2 C. 2
log x − log x = 0 . D. 2
log x − log x + 6 = 0 2 2 2 2 Lời giải Chọn C
Với điều kiện x > 0 : 2
log x − log 8x + 3 = 0 ⇔ 2
log x − log 8 + log x + 3 = 0 ⇔ log x − log x = 0 . 2 ( 2 2 ) 2 2 2 ( ) 2 2
Câu 16. Tập nghiệm của phương trình log (4 − 2x ) = 2 − x là: 2
A. S = ∅ .
B. S =  . C. S = { } 1 .
D. S = (−∞ ) ;1 .
Trang 3/6 - Mã đề thi 114 - https://toanmath.com/ Lời giải Chọn C 2 x x −x x 2
log (4 − 2 ) = 2 − x ⇒ 4 − 2 = 2 ⇔ 4 − 2 = ⇔ − + = ⇔ x = x (2x)2 2 4.2x 4 0 1 2 2
So với điều kiện phương trình S = { } 1 . − −
Câu 17. Nghiệm nguyên dương lớn nhất của bất phương trình: x 1 x 2 4 − 2
≤ 3 thuộc khoảng nào sau đây? A. ( ; −∞ − ) 1 . B. [ 1 − ;2) . C. [2; 4) . D. [4; +∞) . Lời giải Chọn C − − Ta có x 1 x 2 4 − 2 ≤ 1 x 1 3 4 2x ⇔ −
− 3 ≤ 0 ⇔ 0 < 2x ≤ 4 ⇔ x ≤ 2 . 4 4
Câu 18. Để chuẩn bị tiền sau 3 năm nữa cho con lựa chọn học nghề với các gói học phí như sau: gói 1: 150
triệu đồng, gói 2: 200 triệu đồng, gói 3: 250 triệu đồng, gói 4: 300 triệu đồng. Ông A đã gửi số tiền
là 1 tỉ đồng vào một ngân hàng với lãi suất 8% trên một năm . Hỏi sau 3 năm với số tiền lãi của ông
A lĩnh được, con ông A có thể chọn được tối đa bao nhiêu nguyện vọng phù hợp với gói học phí đã nêu? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Ta có: Số tiền ông A nhận được sau 3 năm là: 1000(1+8%)3 ≈1 5 2 9, 712 triệu đồng.
Tiền lãi sau 3 năm là: T =1259,712 −1000 = 259,712 triệu đồng. l
Vậy chọn được tối đa 3 nguyện vọng.
Câu 19. Khi đặt t = log x , x > 0 thì bất phương trình 2 log 5x − 3log
x − 5 ≤ 0 trở thành bất phương 5 ( ) 5 5 trình nào sau đây? A. 2
t − 6t − 4 ≤ 0 . B. 2
t − 6t − 5 ≤ 0 . C. 2
t − 4t − 4 ≤ 0 . D. 2
t − 3t − 5 ≤ 0 . Lời giải Chọn C 2 log 5x − 3log
x − 5 ≤ 0 ⇔ (log x +1 − 6 log x − 5 ≤ 0 2
⇔ log x − 4log x − 4 ≤ 0. 5 )2 5 ( ) 3 5 5 5
Với t = log x bất phương trình trở thành: 2
t − 4t − 4 ≤ 0 . 5
Câu 20. Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 = . 9x m
+1 có đúng 1 nghiệm. A. [1;3) . B. (3; 10 ) . C. { 10} . D. (1; ] 3 ∪{ 10}. Lời giải Chọn D + Đặt t x 3 2
t = 3 , t > 0 ⇒ pt ⇔ t + 3 = . m t +1 ⇔ m = = f (t). 2 t +1 1− 3t 1
Có f ′(t ) = (
⇒ f ′ t = 0 ⇔ 1− 3t = 0 ⇔ t = . 2 t − )3 ( ) 3 1
Ta có bảng biến thiên hàm số f (t ) như sau:
Trang 4/6 - Mã đề thi GỐC - https://toanmath.com/
Dựa vào bảng biến thiên ta thấy, với m∈(1; ]
3 ∪{ 10} thì phương trình đã cho có đúng 1 nghiệm.
Câu 21. Phương trình .2019 x 3.2019 x x − − +
= 0 có tập nghiệm là: A. S = {− } 3 . B. S = { 3 − ; } 2019 . C. S = { } 2019 . D. S = {0; 3 − ; } 2019 . Lời giải Chọn A .2019 x 3.2019 x x − − +
= 0 ⇔ 2019−x (x + 3) = 0 ⇔ x = 3 − Câu 22. Cho hàm số 2 y =
x + 2 − ln x trên đoạn [1; 2]. Giá trị nhỏ nhất của hàm số có dạng a + b ln a ,
với b∈ và a là số nguyên tố. Mệnh đề nào sau đây đúng? A. a = 4 − b .
B. a < b . C. 2 2
a + b = 10 . D. 2
a < 9b . Lời giải Chọn A
Xét trên [1; 2] hàm số liên tục. x 1 y′ = − . 2 + 2 x x 2 2 y′ = 0 ⇔ x + 2 = x . 2 x = 1 − ⇔  ⇒ x = 2 ∈[1;2]. 2 x = 2 y ( )
1 = 3 ; y (2) = 6 − ln 2 ; y ( ) 1 2 = 2 − ln 2 . 2 1 Nên min y = y = −
và max y = y (2) = 6 − ln 2 . ∈ ( 2) 2 ln2 x [1;2] 2 x [ ∈ 1;2]
Câu 23. Bất phương trình: 2 2 2 2020 4038 log
x − 4038 log x + 2019 + x − 2 x + 2
≤ 0 có tập nghiệm là: 2 2 A. 2019 S = 2 ; +∞  ). B. S =( ; −∞ 2020) . C. S = { 2019 2 }.
D. S = (2019; +∞) . Lời giải Chọn C 2 2 2 2020 4038 log
x − 4038 log x + 2019 + x − 2 x + 2 ≤ 0 . 2 2 log x − 2019 = 0 ⇔ ( 2
log x − 2019) + ( x − 2 )2 2 2019 ≤ 0 2019  ⇔ x = 2 . 2 2019 x − 2 = 0 ( 6−2 5)2019.( 5+ )2020 1
Câu 24. Giá trị biểu thức
= a + b , với a,b∈ . Tính 2 6
a − b . 4036 2
Trang 5/6 - Mã đề thi 114 - https://toanmath.com/ A. 4071 − . B. 4016 − . C. 2304 . D. 2019 . Lời giải Chọn C ( 6−2 5)2019.( 5+ )2020 2019 1  5 −1 .( 5 +   )2020 1 Ta có: = 4036 4036 2 2 ( 5 − )1.( 5 + ) 2019 1  .( 5 +   )1 = 4036 2 2019 4 .( 5 + ) 1 = = 4 5 +1 = 80 + 4 2018 ( ) 4 Vậy: 2 6 2 6
a = 80;b = 4 ⇒ a − b = 80 − 4 = 2304.
Câu 25. Gọi S là tập hợp tất cả các giá trị của tham số m để trong tất cả các cặp ( ; x y ) thỏa mãn log
(4x + 4 y − 4) ≥ 1 đồng thời tồn tại duy nhất cặp ( ;
x y ) sao cho 3x − 4 y + m = 0 . Tính tổng 2 2 x + y +2
các giá trị của S . A. 20 . B. 4 . C. 12 . D. 8 . Lời giải Chọn B Ta có 2 2 2 2 log
(4x + 4 y − 4) ≥ 1 ⇔ 4x + 4 y − 4 ≥ x + y + 2 ⇔ 2 ≥ (x − 2) + ( y − 2) (1) 2 2 x + y +2
Lại có tồn tại duy nhất cặp sao cho 3x − 4y + m = 0 . (
 x − )2 +( y − )2 2 2 ≤ 2 Suy ra :  có nghiệm duy nhất. 3
 x − 4y + m = 0
Hay đường thẳng tiếp xúc với hình tròn. 6 − 8 + m m = d( = = 12 2 ⇔ . I ;∆)  5 m = 8 −
Vậy tổng các giá trị của S là 4 .
------------- HẾT -------------
Trang 6/6 - Mã đề thi GỐC - https://toanmath.com/
Document Outline

• Made goc chuong II giai tich 12