Đề kiểm tra giữa kì 1 Toán 10 năm 2020 – 2021 trường THPT Mỹ Đức C – Hà Nội

Đề kiểm tra giữa kì 1 Toán 10 năm 2020 – 2021 trường THPT Mỹ Đức C – Hà Nội được biên soạn theo dạng đề trắc nghiệm khách quan kết hợp với tự luận, mời bạn đọc đón xem

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

16 trang 9 tháng trước

Tác giả:

Profile Thanh Tâm

Trang1
MA TRẬN CHI TIẾT ĐỀ KIỂM TRA GIỮA KỲ I - LỚP 10
NĂM HỌC 2020 - 2021
TRẮC NGHIỆM: 50%
CÁC DẠNG TOÁN
CÁC MỨC ĐỘ ĐÁNH GIÁ
CỘNG
(Câu|Điểm)
Nhận biết
(Câu|STT)
Thông hiểu
(Câu|STT)
Vận dụng
(Câu|STT)
VD cao
(Câu|STT)
Xác định mệnh đề, mệnh đề chứa
biến
1
c1
1
0.2
Xét tính đúng sai của một mệnh đề
1
c13
1
0.2
Xác định một tập hợp; Số phần tử
của tập hợp; Quan hệ giữa
phần tử và tập hợp,…
1
c2
1
0.2
Các phép toán về giao, hợp, hiệu của
hai tập hợp
1
c3
1
0.2
Tập hợp con của một tập hợp, hai
tập hợp bằng nhau
1
c14
1
0.2
Các phép toán về giao, hợp, hiệu của
hai tập hợp
1
c15
1
0.2
Tìm điều kiện của tham số để hai tập
số giao nhau khác rỗng hoặc
tương tự hoặc bài toán có
nội dung thực tế về giao,
h
ợ
p các
t
ập h
ợ
p
1
c21
1
0.2
Tìm tập xác định của hàm số đơn
giản
1
c4
1
0.2
Nhận dạng BBT, hàm số và đồ thị
hàm số (1 công thức)
1
c16
1
0.2
Xác định đỉnh và trục đối xứng của
đồ thị hàm số bậc hai đơn
giản
1
c5
1
0.2
Xác định 3 hệ số hàm số bậc hai,
chiều biến thiên hàm số bậc
hai, nhận dạng đồ thị hàm số
bậc hai, xác định tọa độ giao
điểm,…
1
c17
1
0.2
Điều kiện xác định của phương trình
1
c6
1
0.2
Tìm m để một phương trình là
phương trình bậc 1, 2 hoặc
nhận dạng nghiệm của PT
đơn giản
1
c7
1
0.2
Xét tính chẵn lẻ của hàm số
1
c23
1
0.2
Tìm giá m để 3 điểm thẳng hàng
1
c18
1
0.2
Câu hỏi lý thuyết chung về vectơ
như định nghĩa, phương,
hướng, hai vec tơ bằng nhau
hoặc đếm số vectơ tạo
thành,…
1
c8
1
0.2
Nhận dạng quy tắc 3 điểm, quy tắc
hình bình hành, quy tắc trừ
hai vectơ
1
c9
1
0.2
Tính độ dài véctơ
t
ổ
n
g
, hiệu dùn
g
1
1

Trang2
quy tắc ba điểm, quy tắc
hình bình hành, quy tắc trừ
hai vectơ
c19
0.2
Nhận dạng định nghĩa tích của vec
tơ với 1 số, tính chất trung
điểm, trọng tâm, điều kiện
để hai vec tơ cùng phương,
…
1
c10
1
0.2
Tính độ dài véctơ tổng, hiệu, tích
với 1 số; phân tích 1 vectơ
theo hai vec tơ không cùng
phương.
1
c22
1
0.2
Tìm tập hợp điểm thoả điều kiện cho
trước; tìm điều kiện để 3
điểm thẳng hàng
1
c24
1
0.2
Xác định toạ độ điểm, toạ độ véctơ
đơn
g
iản
1
c11
1
0.2
Sự cùng phương, cùng hướng của 2
véctơ
1
c20
1
0.2
Các câu hỏi lý thuyết về tích vô
hướng
1
c12
1
0.2
Ứng dụng tích vô hướng để tìm độ
dài, tìm quỹ tích, cực trị
hình học, biểu thức tọa độ
của tích vô hướng để tìm
điểm đặc biệt,…
1
c25
1
0.2
TỔNG CỘNG
12
2.4
8
1.6
2
0.4
3
0.6
25
5
TỰ LUẬN: 50%
CÁC DẠNG TOÁN
CÁC MỨC ĐỘ ĐÁNH GIÁ
CỘNG
(Câu
|
Đi
m)
Nhận biết
(Câu|STT)
Thông hiểu
(Câu|STT)
Vận dụng
(Câu|STT)
VD cao
(Câu|STT)
Xác định hàm số bậc hai;
Lập bảng biến thiên và vẽ
đồ thị hàm số bậc
hai
1
c28
1
2
Tìm tập xác định của hàm
s
ố
1
c26
1
1
Xác định tọa độ điểm, véc-
tơ
1
c27
1
1
Phân tích một vectơ theo 2
vectơ không cùng
phương cơ bản
1
c29
1
1
TỔNG CỘNG
0
0
2
2
2
3
1
4
5

Trang3
Trường THPT Mỹ Đức C
Tổ Toán - Lý
ĐỀ KIỂM TRA GIỮA KÌ I LỚP 10
NĂM HỌC 2020-2021
Thời gian : 90 phút
ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (25 CÂU TRẮC NGHIỆM – 5,0 ĐIỂM)
Câu 1. Trong các câu sau, câu nào là mệnh đề chứa biến?
A. 18 là số chính phương.
B. Hình chữ nhật có hai đường chéo bằng nhau.
C.
2
5,xx x
.
D. 9 là số nguyên tố.
Câu 2. Cho tập hợp
;;;
A
abcd
, phát biểu nào là sai?
A.
aA
. B.
;ad A
. C.
;bc A
. D.
dA
.
Câu 3. Cho tập hợp
5; 3A 
. Tập CA
là
A.
;5
. B.
5; 
. C.
3; 
. D.

;5 3; 
.
Câu 4. Tìm tập xác định hàm số
1
x
y
x

.
A.
1; 
. B.
1; 
. C.
;1
. D.
;1
.
Câu 5. Cho hàm số
2
21
y
xx
có đồ thị
P
. Đỉnh của

P
là
A.
17
;
48
I



. B.
111
;
48
I



. C.
1
;1
2
I



. D.
1
;2
2
I



.
Câu 6. Điều kiện nào để khi bình phương 2 vế phương trình sau ta được một phương trình tương
đương:
2
46 2xx x.
A.
x
. B.
2x
. C.
2x
. D.
2x 
.
Câu 7. Nghiệm của phương trình
10xx
là
A.
0x
. B.
1x
. C.
2x
. D.
1x 
.
Câu 8. Số các vectơ (khác
0
) có điểm đầu và điểm cuối là các đỉnh của hình vuông
A
BCD
.
A.
10
. B.
11
. C.
12
. D.
13
.
Câu 9. Chọn khẳng định đúng trong các hệ thức sau:
A.
A
BACBC
  
. B.
M
PNM NP
  
. C.
CA BA CB
 
. D. AA BB AB
 
.
Câu 10. Cho đoạn thẳng
A
B
, hình nào sau đây biểu diễn đúng điểm
M
thỏa mãn:
40MA MB
 

Trang4
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 11. Cho
(2; ), 3; 1 , ;5ubv wa

. Vectơ
wuv

nếu:
A.
5; 6ab
. B.
5; 3ab
. C.
4; 4ab
. D.
3; 4ab
.
Câu 12. Cho
a
và
b
là hai vectơ khác vectơ
0
. Chọn đáp án đúng trong các đáp án sau:
A. Tích vô hướng của
a
và
b
là một véc tơ khác vectơ
0
.
B. Tích vô hướng của
a
và
b
là một số khác 0.
C. Tích vô hướng của
a
và
b
là một số bằng 0.
D. Tích vô hướng của
a
và
b
là một số thực.
Câu 13. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai?
A. Tam giác
A
BC
cân thì tam giác có hai cạnh bằng nhau.
B. Số thực
a
chia hết cho
6
thì
a
chia hết cho
2
và
3
.
C. Tứ giác
A
BCD
là hình bình hành thì
A
B
song song với CD.Câu 14. Cho tập hợp
1; 2; 4; 6A
. Có
tất cả bao nhiêu tập hợp con của
A
có chứa phần tử
1
?
A.
9 . B. 8 . C. 6. D.
7
.
Câu 15. Cho hai tập hợp

2;3 , 1;AB
. Khi đó
CAB
bằng
A.
1; 3 .
B.

;1 3; . 
C.
3; .
D.
;2.
Câu 16. Cho hàm số bậc 2 có BBT sau:
Trong các hàm số sau, hàm số nào có BBT như trên?
A.
2
23yx x
. B.
2
21
y
xx
. C.
2
25yx x
. D.
2
22yx x
Câu 17. Cho hàm số
2
yax bxc
có đồ thị như hình vẽ

Trang5
Xác định các hệ số
,,abc
A.
1, 2, 2abc 
B.
1, 2, 2abc 
C.
1, 2, 1ab c
D.
1, 2, 0abc 
Câu 18 . Trong mặt phẳng
Oxy
, cho ba điểm

1; 2 , 2; 5 2 , 3; 4Am B m Cm
. Tính giá trị của
tham số
m
để ba điểm
,,ABC
thẳng hàng .
A.
3m
. B.
2m 
. C.
1m
. D.
2m
.
Câu 19. Tam giác
A
BC
có
A
BACa
và
120BAC 
. Tính
.
A
BAC

A.
3.AB AC a

B.
.
A
BAC a

C.
.
2
a
AB AC

D.
2.
A
BAC a
 
Câu 20. Cho lục giác đều
A
BCDEF
tâm
.O
Số các vectơ khác vectơ - không, cùng phương với
OC

có
điểm đầu và điểm cuối là các đỉnh của lục giác là
A.
4.
B.
6.
C.
7.
D.
9.
Câu 21. Cho hai tập hợp

21;25Mm m
và
1; 7Nm m
. Số các giá trị nguyên của tham số
m
sao cho
MN
là
A.
10
. B.
11
. C.
12
. D.
13
.
Câu 22. Cho tam giác
A
BC , điểm
I
thỏa mãn
253 0IA IB IC

, điểm
K
thỏa mãn
;AK xAB x
 
. Xác định
x
để ba điểm
;;CKI
thẳng hàng.
A.
1
3
. B.
2
3
. C.
5
7
. D.
3
7
.
Câu 23. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
2
1
1
x
y
x
. B.
1
y
x
. C.
y
xx
. D.
2
22yx x
.
Câu 24. Cho tam giác
A
BC
. Gọi ,DE lần lượt là các điểm thỏa mãn:
2
3
BD BC
 
,
1
4
A
EAC

. Gọi
B
E cắt
A
D
tại K . Tỉ số
A
K
A
D
bằng
A.
1
3
. B.
2
5
. C.
3
5
. D.
1
4
.
Câu 25. Cho tam giác ABC đều cạnh
3a
. Lấy các điểm ,
M
N lần lượt trên các cạnh
,BC CA
sao cho
B
Ma
,
2CN a
. Gọi
P
là điểm trên cạnh
A
B
sao cho
A
M
vuông góc
PN
. Độ dài
PN
theo
a là

Trang6
A.
21
5
a
. B.
3
a
. C.
5
3
a
. D.
2
5
a
.
II. PHẦN TỰ LUẬN (4 CÂU TỰ LUẬN – 5,0 ĐIỂM)
Bài 26.
Tìm tập xác định các hàm số sau:
a.
2
21
6
x
y
xx

. b.
21 32
2
xx
y
x

Bài 27. Trong mặt phẳng tọa độ
Oxy
, cho ba điểm
3; 3A
,

4; 2B
,
1; 1C 
.
a. Tính tọa độ véc tơ
AB

,
A
C

.
b. Tìm tọa độ điểm
M
thỏa mãn
40MA MB MC
  
Câu 28. Xác định hàm số
2
yax bxc
biết đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ là
1;2
và cắt trục tung tại điểm có tung độ bằng
2
. Lập bảng biến thiên và vẽ đồ thị của hàm số
vừa tìm được.
Câu 29. Cho
A
BC có trọng tâm G ,
H
là điểm đối xứng với
B
qua G . Gọi
M
là trung điểm đoạn
BC
. Đặt ;
A
BbACc
 
. Biểu thị các vectơ ;;
A
HCHMH
  
theo hai vectơ ;bc

.
HẾT

Trang7
ĐÁP ÁN THAM KHẢO
ĐÁP ÁN PHẦN TRẮC NGHIỆM
1.C 2.B 3.D 4.D 5.A 6.B 7.B 8.C 9.B 10.D
11.A 12.D 13.C 14.B 15.D 16.B 17.A 18.D 19.B 20.B
21.C 22.C 23.D 24.A 25.A
ĐÁP ÁN CHI TIẾT
PHẦN TRẮC NGHIỆM
Câu 1. Trong các câu sau, câu nào là mệnh đề chứa biến?
A. 18 là số chính phương.
B. Hình chữ nhật có hai đường chéo bằng nhau.
C.

2
5,xx x
.
D. 9 là số nguyên tố.
Lời giải
Chọn C
Câu 2. Cho tập hợp
;;;
A
abcd
, phát biểu nào là sai?
A.
aA
. B.
;ad A
. C.
;bc A
. D.
dA
.
Lời giải
Chọn B
Câu 3. Cho tập hợp
5; 3A 
. Tập
CA
là
A.

;5
. B.
5; 
. C.
3; 
. D.
;5 3; 
.
Lời giải
Chọn D
Câu 4. Tìm tập xác định hàm số
1
x
y
x

.
A.
1; 
. B.
1; 
. C.
;1
. D.
;1
.
Lời giải
Chọn D

Trang8
Điều kiện
10 1
x
x
.
Vậy

;1D 
.
Câu 5. Cho hàm số
2
21
y
xx
. Đỉnh của
P
là
A.
17
;
48



I
. B.
111
;
48



I
. C.
1
;1
2



I
. D.
1
;2
2



I
.
Lời giải
Chọn A
Đỉnh
P
là
1
24
b
x
a

thế
1
4
x
vào
2
21
y
xx
.
Ta được
7
8
y
17
;
48
I




.
Câu 6. Điều kiện nào để khi bình phương 2 vế phương trình sau ta được một phương trình tương
đương:
2
46 2
x
xx
.
A.
x
. B.
2x
. C.
2x
. D.
2x 
.
Lời giải
Chọn B
Điều kiện
2
460
2
20
x
xx
x
x




Vậy
2x
.
Câu 7. Nghiệm của phương trình
10xx
là
A.
0
x
. B.
1
x
. C.
2
x
. D.
1
x

.
Lời giải
Chọn B
Điều kiện:
1
x
10 10 10 1
x
xxxx 
Câu 8. Số các vectơ (khác
0
) có điểm đầu và điểm cuối là các đỉnh của hình vuông
ABCD
.
A.
10
. B.
11
. C.
12
. D.
13
.
Lời giải
Chọn C
Cách
1
: Có
6
đoạn thẳng nối từ các đỉnh của hình vuông
ABCD
, mà mỗi đoạn thẳng tạo
thành hai vectơ nên lập được
12
vectơ.
Cách
2
: cố định
1
điểm làm gốc thì có
3
vectơ là lấy
3
điểm còn lại làm ngọn. Do vai trò của
4
điểm như nhau nên có
4.312
vectơ.
Câu 9. Chọn khẳng định đúng trong các hệ thức sau:
A.
A
BAC BC
  
. B.
M
PNM NP
 
. C.
CA BA CB

. D.
A
ABB AB
 
.
Lời giải

Trang9
Chọn B
Cách
1
: Theo quy tắc trừ ta có:
M
PNM NP MP NPNM MPMP
       
(đúng).
Cách
2
:
0VT MN NP NM MN NM NP NP NP VP
   
Câu 10. Cho đoạn thẳng
A
B
, hình nào sau đây biểu diễn đúng điểm
M
thỏa mãn: 40MA MB
 
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Lời giải
Chọn D
Ta có 40 4
M
AMB MA MB
   
.
Do đó
4.
M
AMA
;
M
A

và
M
B

ngược hướng.
Câu 11. Cho
(2; ), 3; 1 , ;5ubv wa

. Vectơ
wuv

nếu:
A.
5; 6ab
. B.
5; 3ab
. C.
4; 4ab
. D.
3; 4ab
.
Lời giải
Chọn A
Ta có:
23 5
5(1) 6
aa
wuv
bb







.
Câu 12. Cho
a
và
b
là hai vectơ khác vectơ
0
. Chọn đáp án đúng trong các đáp án sau:
A. Tích vô hướng của
a và b
là một véc tơ khác vectơ 0
.
B. Tích vô hướng của
a và b
là một số khác 0.
C. Tích vô hướng của
a và b
là một số bằng 0.
D. Tích vô hướng của
a và b
là một số thực.
Lời giải
Chọn D
Tích vô hướng của
a và b
là một số thực.
Câu 13. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai?
A.
Tam giác
A
BC
cân thì tam giác có hai cạnh bằng nhau.
B.
Số thực
a
chia hết cho
6
thì
a
chia hết cho
2
và
3
.
C. Tứ giác
A
BCD
là hình bình hành thì
A
B
song song với
CD
.
D. Tứ giác
A
BCD
là hình chữ nhật thì tứ giác có ba góc vuông.
Lời giải
Chọn C

Trang10
Vì nếu tứ giác ABCD có AB song song với CD thì tứ giác có thể là hình thang không là hình
bình hành.
Câu 14. Cho tập hợp
1; 2; 4; 6A
. Có tất cả bao nhiêu tập hợp con của
A
có chứa phần tử
1
?
A.
9
. B.
8
. C.
6
. D.
7
.
Lời giải
Chọn B
Số tập con của tập hợp
2; 4; 6
là 8 . Lấy mỗi tập con đó và thêm vào phần tử
1
ta được tập
con của tập hợp
1; 2; 4; 6A
thỏa mãn đề bài.
Vậy có tất cả
8 tập con thỏa mãn đề bài.
Câu 15. Cho hai tập hợp

2;3 , 1;AB
. Khi đó
CAB
bằng
A.
1; 3 .
B.

;1 3; . 
C.
3; .
D.
;2.
Lời giải
Chọn D
Ta có:
2;AB

\CAB AB
;2CAB
.
Câu 16. Cho hàm số bậc 2 có BBT sau:
Trong các hàm số sau, hàm số nào có BBT như trên?
A.
2
23yx x
. B.
2
21yx x
. C.
2
25yx x
. D.
2
22yx x
Lời giải
Chọn B
Câu 17. Cho hàm số
2
y
ax bx c
có đồ thị như hình vẽ
Xác định các hệ số
,,abc
A.
1, 2, 2abc 
B.
1, 2, 2abc 
C.
1, 2, 1ab c
D.
1, 2, 0abc 

Trang11
Lời giải
Chọn A
Vì đồ thị hàm số cắt trục
Ox
tại điểm có tung độ là
2
nên
2c 
.
Mặt khác đồ thị hàm số nhận điểm
(1; 1)I
làm đỉnh nên
22
0
1
22
1
2
1
2
44 484
1
2
4
b
a
ba ba
a
a
a
b
baca aaa
ba
a


 












(vì 2c  và
0a
)
Vậy
1, 2, 2abc 
Dựa vào BBT ta thấy đồ thị hàm số nhận điểm
(1; 2)I
làm đỉnh và có hệ số
0a
nên ta chọn
hàm số
2
21yx x
.
Câu 18 . Trong mặt phẳng
Oxy
, cho ba điểm
1; 2 , 2; 5 2 , 3; 4Am B m Cm
. Tính giá trị của
tham số
m
để ba điểm
,,ABC
thẳng hàng .
A. 3m . B. 2m  . C.
1m
. D. 2m .
Lời giải
Chọn D
Ta có

3;32, 2;2AB m m AC

Ba điểm
,,ABC
thẳng hàng
A
B

và
A
C

cùng phương
332
2
22
mm
m


.
Câu 19. Tam giác
A
BC
có
A
BACa
và
120BAC 
. Tính
.
A
BAC
 
A.
3.AB AC a
 
B.
.
A
BAC a

C.
.
2
a
AB AC
 
D.
2.
A
BAC a
 
Lời giải
Chọn B
Gọi
M
là trung điểm
.
B
CAMBC
Trong tam giác vuông
A
MB
, ta có
0
.sin .sin 30 .
2
a
AM AB ABM a
Ta có
22 .
A
BAC AM AM a
  
Câu 20. Cho lục giác đều
A
BCDEF
tâm
.O
Số các vectơ khác vectơ - không, cùng phương với OC

có
điểm đầu và điểm cuối là các đỉnh của lục giác là
A.
4.
B.
6.
C.
7.
D.
9.
Lời giải
M
C
B
A

Trang12
Chọn B
Đó là các vectơ:
,, , , ,
A
BBADEEDFCCF
    
.
Câu 21. Cho hai tập hợp
21;25Mm m
và
1; 7Nm m
. Số các giá trị nguyên của tham số
m
sao cho MN là
A. 10 . B.
11
. C.
12
. D. 13 .
Lời giải
Chọn C
Xét
25 1 4
21 7 8
mm m
MN
mm m



.
Suy ra
48MN m
.
Vậy có 12 giá trị
m
nguyên.
Câu 22. Cho tam giác
A
BC , điểm
I
thỏa mãn
253 0IA IB IC

, điểm
K
thỏa mãn
;AK x AB x
 
. Xác định
x
để ba điểm
;;CKI
thẳng hàng.
A.
1
3
. B.
2
3
. C.
5
7
. D.
3
7
.
Lời giải
Chọn C
Ta có
25
33
CI IA IB
 
.
Theo giả thiết
A
KxAB
 

I
KIAxIBIA
 
.
1IK x IA xIB
 
.
Ba điểm
;;CKI
thẳng hàng ;IK CI
 
cùng phương.

15
51 2
25
7
33
xx
xxx

.
Câu 23. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
2
1
1
x
y
x
. B.
1
y
x
. C.
y
xx
. D.
2
22yx x
.

Trang13
Lời giải
Chọn D
Xét hàm số

2
22yfx x x
có tập xác định
D
.
Suy ra

1xx 
.
Mặt khác,
 
2
2
22 22 2fx x x x x fx
.
Từ

1,2
suy ra hàm số

2
22yfx x x
là hàm số chẵn.
Câu 24. Cho tam giác
ABC
. Gọi
,DE
lần lượt là các điểm thỏa mãn:
2
3
BD BC
 
,
1
4
AE AC
 
. Gọi
BE
cắt
AD
tại
K
. Tỉ số
AK
AD
bằng
A.
1
3
. B.
2
5
. C.
3
5
. D.
1
4
.
Lời giải
Chọn A
Vì

113
1
444
AE AC BE BC BA
  
.
Giả sử

..1.AK x AD BK x BD x BA
    
.
Mà
2
3
BD BC
 
nên

2
.1.
3
x
BK BC x BA
  
.
Vì
,,BKE
thẳng hàng

BE
nên có
m
sao cho
.BK m BE
 
.
Do đó ta có:

23
.1.
344
xmm
BC x BA BC BA
 
. Hay
23
10
43 4
mx m
BC x BA




 
.
Do
,BC BA
 
không cùng phương nên ta có:
8
2
0
9
43
1
3
10
3
4
mx
m
m
x
x





.
Vậy
1
3
AK
AD
.

Trang14
Câu 25. Cho tam giác ABC đều cạnh
3a
. Lấy các điểm
,MN
lần lượt trên các cạnh
,BC CA
sao cho
BM a
,
2CN a
. Gọi
P
là điểm trên cạnh
AB
sao cho
AM
vuông góc
PN
. Độ dài
PN
theo
a
là
A.
21
5
a
.
B.
3
a
.
C.
5
3
a
.
D.
2
5
a
.
Lời giải
Chọn A
Đặt

.0AP x AB x

 
.
Ta có:

11 21
33 33
AM AB BM AB BC AB AC AB AB AC  
      
.
1
.
3
PN PA AN x AB AC
    
.
Do
AM PN
nên:
21 1
.0 .. 0
33 3
AM PN AB AC x AB AC




     
2
22 2
2
22
212 9
(3 ) (3 ) . 0 . 9 cos 60
3993 2
29
60
93 2
29 4
61 0
932 15
xx a
a a AB AC AB AC a
xa
xa a
x
xx















 
Khi đó:
2
2
2
22 2
41 41
..
15 3 15 3
16 1 8 9 21
(3 ) (3 ) .
225 9 45 2 25
PN AB AC PN AB AC
a
aa a





    
21
5
a
PN
.

Trang15
PHẦN TỰ LUẬN
Bài 26. Tìm tập xác định các hàm số sau:
a.
2
21
6
x
y
xx

. b.
21 32
2
xx
y
x

Lời giải
a
. Điều kiện xác định:
2
2
60
3
x
xx
x


.
Vậy
\2;3D 
.
b. Điều kiện xác định:
210
320
20
x
x
x



1
2
2
3
2
x
x
x

1
2
2
x
x
.
Vậy tập xác định của hàm số là

1
;\2
2
D



.
Bài 27. Trong mặt phẳng tọa độ
Oxy
, cho ba điểm
3; 3A
,

4; 2B
,
1; 1C 
.
a. Tính tọa độ véc tơ AB

,
A
C

.
b. Tìm tọa độ điểm
M
thỏa mãn
40MA MB MC
  
Lời giải
a.
Ta có
1; 5AB

,
4; 4AC 

.
b. Ta có
40MA MB MC
  


344 1 0
342 1 0
MM M
MMM
xx x
yyy


5
1
M
M
x
y

Vậy điểm
5; 1M
.
Câu 28. Xác định hàm số
2
y
ax bx c
biết đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ là
1;2
và cắt trục tung tại điểm có tung độ bằng
2
. Lập bảng biến thiên và vẽ đồ thị của hàm số
vừa tìm được.
Lời giải
+ Theo bài ra ta có:
01
42 0 1
22
abc a
abc b
cc








.
Hàm số cần tìm là:
2
2yxx
.
+ Bảng biến thiên:

Trang16
+ Vẽ đồ thị hàm số:
Đồ thị hàm số có: + Đỉnh
19
;
24
I



.
+ Trục đối xứng:
1
2
x
.
+ Giao với trục hoành:

1;0 ; 2;0
.
+ Giao với trục tung:
0;2
.
Câu 29. Cho
A
BC
có trọng tâm
G
,
H
là điểm đối xứng với
B
qua
G
. Gọi
M
là trung điểm đoạn
BC
. Đặt ;
A
BbACc
 
. Biểu thị các vectơ ;;
A
HCHMH
  
theo hai vectơ ;bc

.
Lời giải
+ Ta có:

42
22
33
A
HAB AG AH AB AG AB AM AB ABAC
      
12 12
33 33
A
BAC bc 
 
+
21 2 1 11 11
33 3 3 33 33
CH CA CB AC AB AC AB AC b c
      
.
+
111 51
233 66
M
HMCCH BC AB AC b c
   
.
HẾT
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


MA TRẬN CHI TIẾT ĐỀ KIỂM TRA GIỮA KỲ I - LỚP 10 NĂM HỌC 2020 - 2021
TRẮC NGHIỆM: 50%
CÁC MỨC ĐỘ ĐÁNH GIÁ CỘNG CÁC DẠNG TOÁN
Nhận biết Thông hiểu Vận dụng VD cao (Câu|Điểm) (Câu|STT)
(Câu|STT) (Câu|STT) (Câu|STT)
Xác định mệnh đề, mệnh đề chứa 1 1 biến c1 0.2 1 1
Xét tính đúng sai của một mệnh đề c13 0.2
Xác định một tập hợp; Số phần tử 1 1
của tập hợp; Quan hệ giữa c2 0.2
phần tử và tập hợp,…
Các phép toán về giao, hợp, hiệu của 1 1 hai tập hợp c3 0.2
Tập hợp con của một tập hợp, hai 1 1 tập hợp bằng nhau c14 0.2
Các phép toán về giao, hợp, hiệu của 1 1 hai tập hợp c15 0.2
Tìm điều kiện của tham số để hai tập
số giao nhau khác rỗng hoặc 1 1
tương tự hoặc bài toán có c21 0.2
nội dung thực tế về giao, hợp các tập hợp
Tìm tập xác định của hàm số đơn 1 1 giản c4 0.2
Nhận dạng BBT, hàm số và đồ thị 1 1 hàm số (1 công thức) c16 0.2
Xác định đỉnh và trục đối xứng của 1 1
đồ thị hàm số bậc hai đơn c5 0.2 giản
Xác định 3 hệ số hàm số bậc hai,
chiều biến thiên hàm số bậc 1 1
hai, nhận dạng đồ thị hàm số c17 0.2
bậc hai, xác định tọa độ giao điểm,… 1 1
Điều kiện xác định của phương trình c6 0.2
Tìm m để một phương trình là
phương trình bậc 1, 2 hoặc 1 1
nhận dạng nghiệm của PT c7 0.2 đơn giản 1 1
Xét tính chẵn lẻ của hàm số c23 0.2 1 1
Tìm giá m để 3 điểm thẳng hàng c18 0.2
Câu hỏi lý thuyết chung về vectơ
như định nghĩa, phương, 1 1
hướng, hai vec tơ bằng nhau c8 0.2
hoặc đếm số vectơ tạo thành,…
Nhận dạng quy tắc 3 điểm, quy tắc 1 1
hình bình hành, quy tắc trừ c9 0.2 hai vectơ
Tính độ dài véctơ tổng, hiệu dùng 1 1 Trang 1
quy tắc ba điểm, quy tắc c19 0.2
hình bình hành, quy tắc trừ hai vectơ
Nhận dạng định nghĩa tích của vec
tơ với 1 số, tính chất trung 1 1
điểm, trọng tâm, điều kiện c10 0.2
để hai vec tơ cùng phương, …
Tính độ dài véctơ tổng, hiệu, tích
với 1 số; phân tích 1 vectơ 1 1 theo hai vec tơ không cùng c22 0.2 phương.
Tìm tập hợp điểm thoả điều kiện cho 1 1
trước; tìm điều kiện để 3 c24 0.2 điểm thẳng hàng
Xác định toạ độ điểm, toạ độ véctơ 1 1 đơn giản c11 0.2
Sự cùng phương, cùng hướng của 2 1 1 véctơ c20 0.2
Các câu hỏi lý thuyết về tích vô 1 1 hướng c12 0.2
Ứng dụng tích vô hướng để tìm độ
dài, tìm quỹ tích, cực trị 1 1
hình học, biểu thức tọa độ c25 0.2
của tích vô hướng để tìm điểm đặc biệt,… 12 8 2 3 25 TỔNG CỘNG 2.4 1.6 0.4 0.6 5 TỰ LUẬN: 50% CỘNG
CÁC MỨC ĐỘ ĐÁNH GIÁ CÁC DẠNG TOÁN (Câu|Điểm)
Nhận biết Thông hiểu Vận dụng VD cao (Câu|STT) (Câu|STT) (Câu|STT) (Câu|STT)
Xác định hàm số bậc hai;
Lập bảng biến thiên và vẽ 1 1 đồ thị hàm số bậc c28 2 hai
Tìm tập xác định của hàm 1 1 số c26 1
Xác định tọa độ điểm, véc- 1 1 tơ c27 1
Phân tích một vectơ theo 2 1 1 vectơ không cùng c29 1 phương cơ bản 0 2 2 1 4 TỔNG CỘNG 0 2 3 5 Trang 2
Trường THPT Mỹ Đức C
ĐỀ KIỂM TRA GIỮA KÌ I LỚP 10 Tổ Toán - Lý NĂM HỌC 2020-2021 Thời gian : 90 phút ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (25 CÂU TRẮC NGHIỆM – 5,0 ĐIỂM) Câu 1.
Trong các câu sau, câu nào là mệnh đề chứa biến?
A. 18 là số chính phương.
B. Hình chữ nhật có hai đường chéo bằng nhau. C.  2
x x5, x  .
D. 9 là số nguyên tố. Câu 2.
Cho tập hợp A  a; ; b ;
c d , phát biểu nào là sai?
A. a A . B.  ; a d  A . C.  ; b c A.
D. d  A . Câu 3.
Cho tập hợp A   5;   3 . Tập C A là  A.  ;    5 . B. 5; . C. 3; . D.  ;  5   3;. x Câu 4.
Tìm tập xác định hàm số y  . x 1
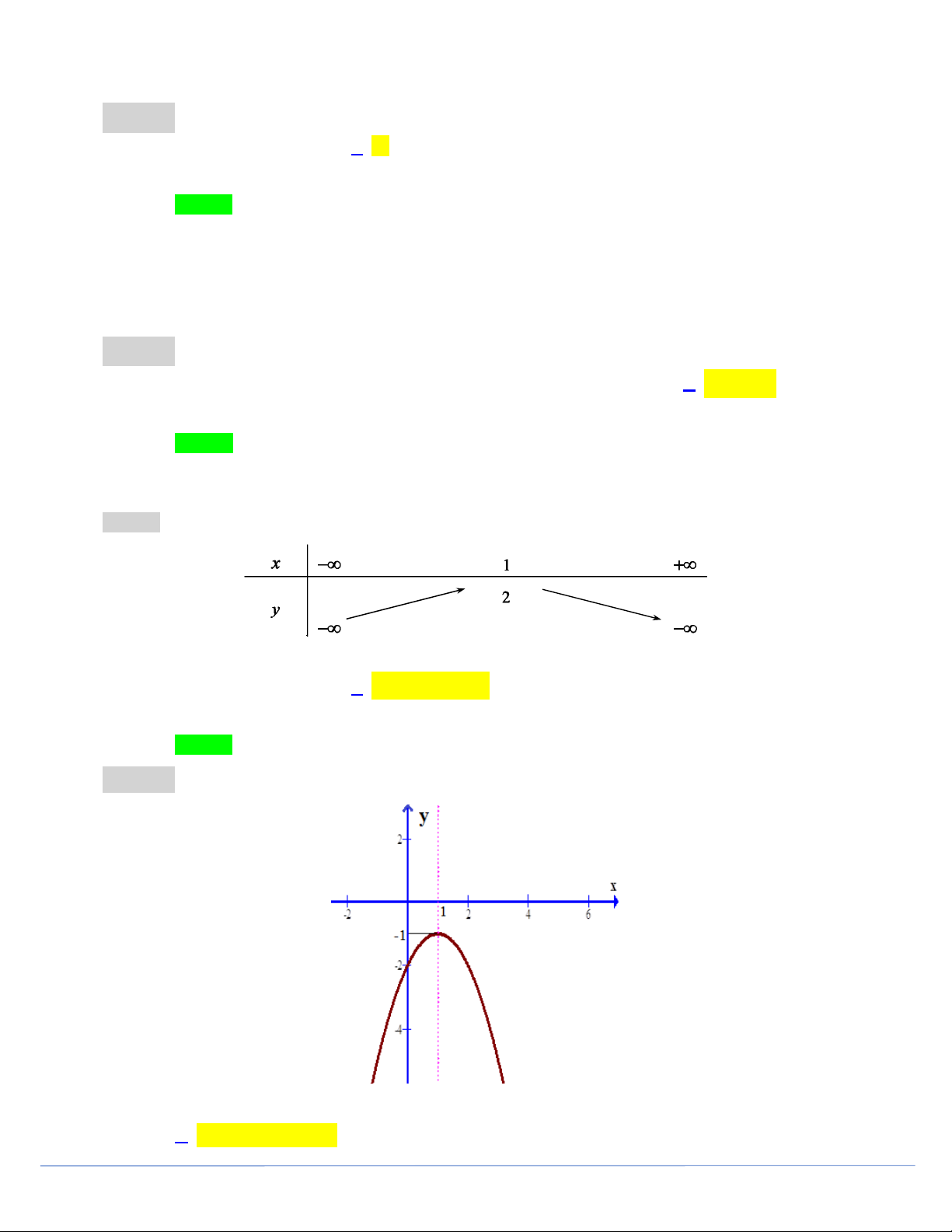
A. 1; . B. 1; . C.   ;1  . D.   ;1  . Câu 5. Cho hàm số 2
y  2x x 1 có đồ thị P . Đỉnh của P là  1 7   1 11  1   1  A. I ;   . B. I  ;   . C. I ;1   . D. I  ;2   .  4 8   4 8   2   2  Câu 6.
Điều kiện nào để khi bình phương 2 vế phương trình sau ta được một phương trình tương đương: 2
x  4x  6  x  2 .
A. x   . B. x  2 . C. x  2 . D. x  2  . Câu 7.
Nghiệm của phương trình x x 1  0 là A. x  0 . B. x  1 . C. x  2 .
D. x  1. Câu 8.
Số các vectơ (khác 0 ) có điểm đầu và điểm cuối là các đỉnh của hình vuông ABCD . A. 10 . B. 11. C. 12 . D. 13 . Câu 9.
Chọn khẳng định đúng trong các hệ thức sau:            
A. AB AC BC .
B. MP NM NP . C. CA BA CB .
D. AA BB AB .   
Câu 10. Cho đoạn thẳng AB , hình nào sau đây biểu diễn đúng điểm M thỏa mãn: MA  4MB  0 Trang 3 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.      
Câu 11. Cho u  (2;b), v   3;  1 , w  
a;5 . Vectơ w u v nếu:
A. a  5; b  6 .
B. a  5; b  3 .
C. a  4; b  4 .
D. a  3; b  4 .   
Câu 12. Cho a và b là hai vectơ khác vectơ 0 . Chọn đáp án đúng trong các đáp án sau:   
A. Tích vô hướng của a và b là một véc tơ khác vectơ 0 .  
B. Tích vô hướng của a và b là một số khác 0.  
C. Tích vô hướng của a và b là một số bằng 0.  
D. Tích vô hướng của a và b là một số thực.
Câu 13. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai?
A. Tam giác ABC cân thì tam giác có hai cạnh bằng nhau.
B. Số thực a chia hết cho 6 thì a chia hết cho 2 và 3.
C. Tứ giác ABCD là hình bình hành thì AB song song với CD.Câu 14. Cho tập hợp A  1;2;4;  6 . Có
tất cả bao nhiêu tập hợp con của A có chứa phần tử 1? A. 9 . B. 8 . C. 6. D. 7 .
Câu 15. Cho hai tập hợp A   2; 
3, B  1; . Khi đó C bằng
  A BA. 1;  3 . B.  
;1 3;. C. 3;. D.  ;  2  .
Câu 16. Cho hàm số bậc 2 có BBT sau:
Trong các hàm số sau, hàm số nào có BBT như trên? A. 2
y x  2x  3 . B. 2
y  x  2x 1. C. 2
y  x  2x  5 . D. 2
y  x  2x  2 Câu 17. Cho hàm số 2
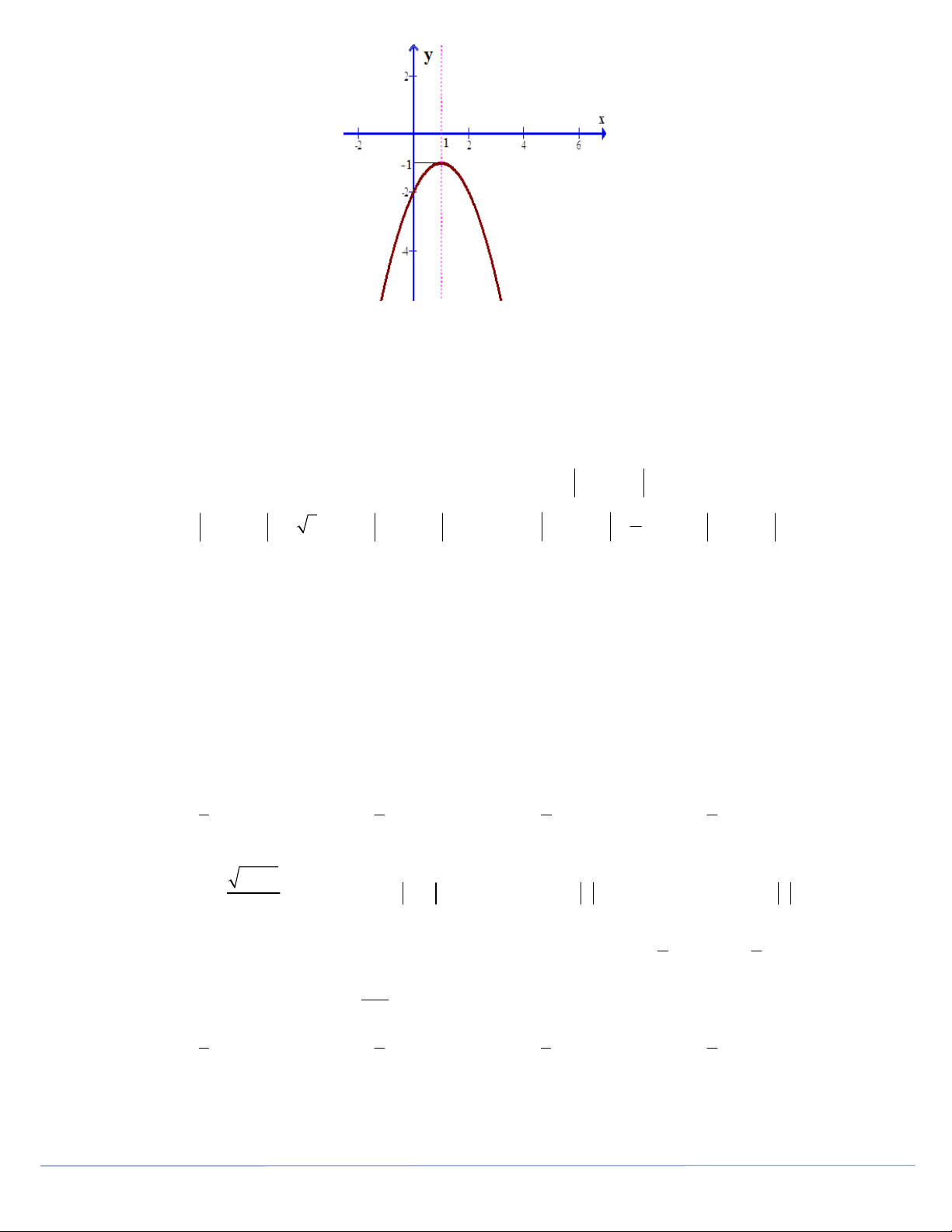
y ax bx c có đồ thị như hình vẽ Trang 4
Xác định các hệ số a, , b c
A. a  1,b  2, c  2 B. a  1,b  2, c  2 C. a  1,b  2,c  1 D. a  1,b  2, c  0
Câu 18 . Trong mặt phẳng Oxy , cho ba điểm Am 1;2, B2;5  2m,C m 3;4 . Tính giá trị của
tham số m để ba điểm ,
A B,C thẳng hàng . A. m  3 . B. m  2  . C. m  1.
D. m  2 .  
Câu 19. Tam giác ABC có AB AC a và 
BAC  120 . Tính AB AC .       a  
A. AB AC a 3.
B. AB AC a.
C. AB AC  .
D. AB AC  2a. 2 
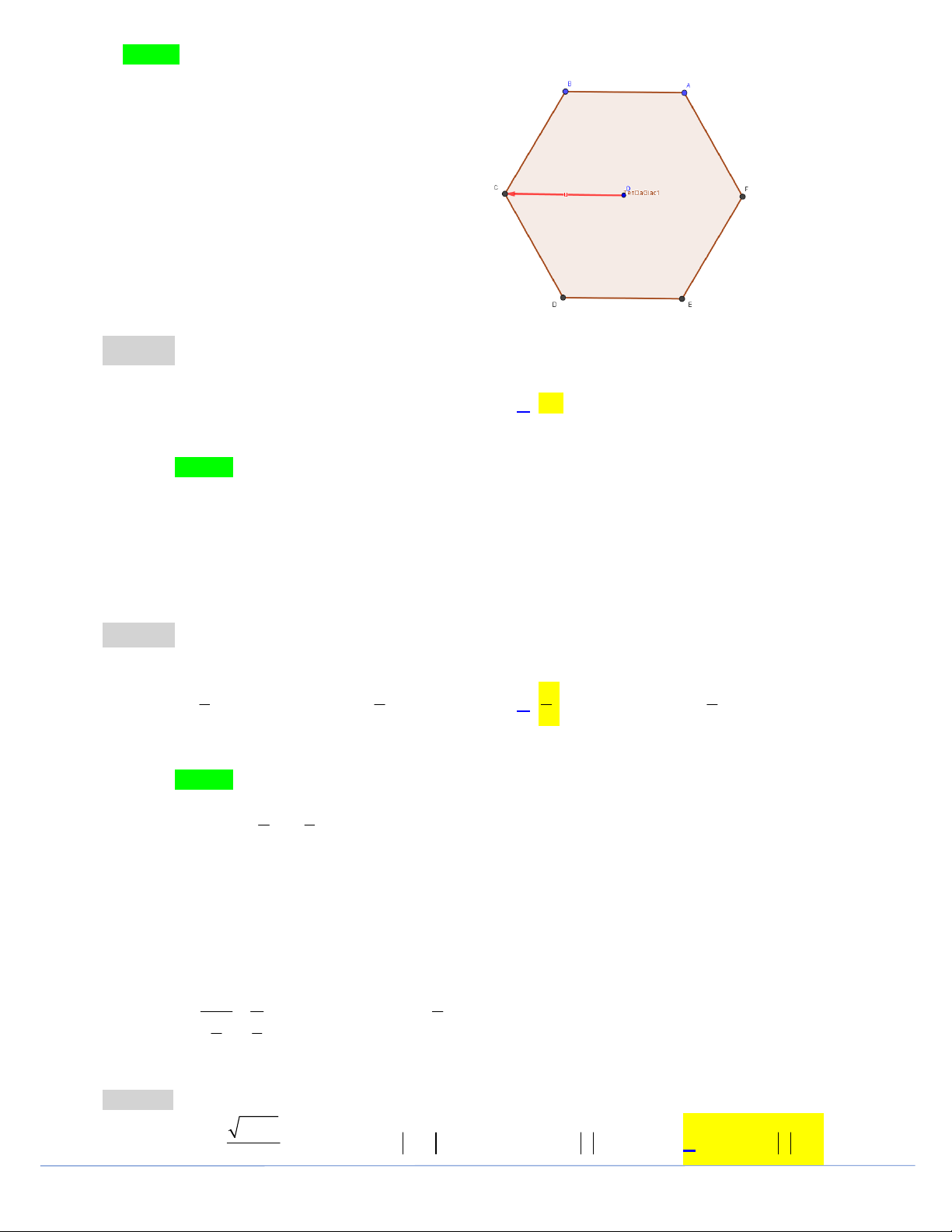
Câu 20. Cho lục giác đều ABCDEF tâm .
O Số các vectơ khác vectơ - không, cùng phương với OC có
điểm đầu và điểm cuối là các đỉnh của lục giác là A. 4. B. 6. C. 7. D. 9.
Câu 21. Cho hai tập hợp M  2m 1;2m  
5 và N  m 1;m  7 . Số các giá trị nguyên của tham số
m sao cho M N   là A. 10 . B. 11. C. 12 . D. 13 .    
Câu 22. Cho tam giác ABC , điểm I thỏa mãn 2IA  5IB  3IC  0 , điểm K thỏa mãn  
AK x AB; x   . Xác định x để ba điểm C ; K ; I thẳng hàng. 1 2 5 3 A. . B. . C. . D. . 3 3 7 7
Câu 23. Trong các hàm số sau, hàm số nào là hàm số chẵn? 2 x 1 A. y  .
B. y x 1 .
C. y x x . D. 2
y x  2 x  2 . x 1  2   1 
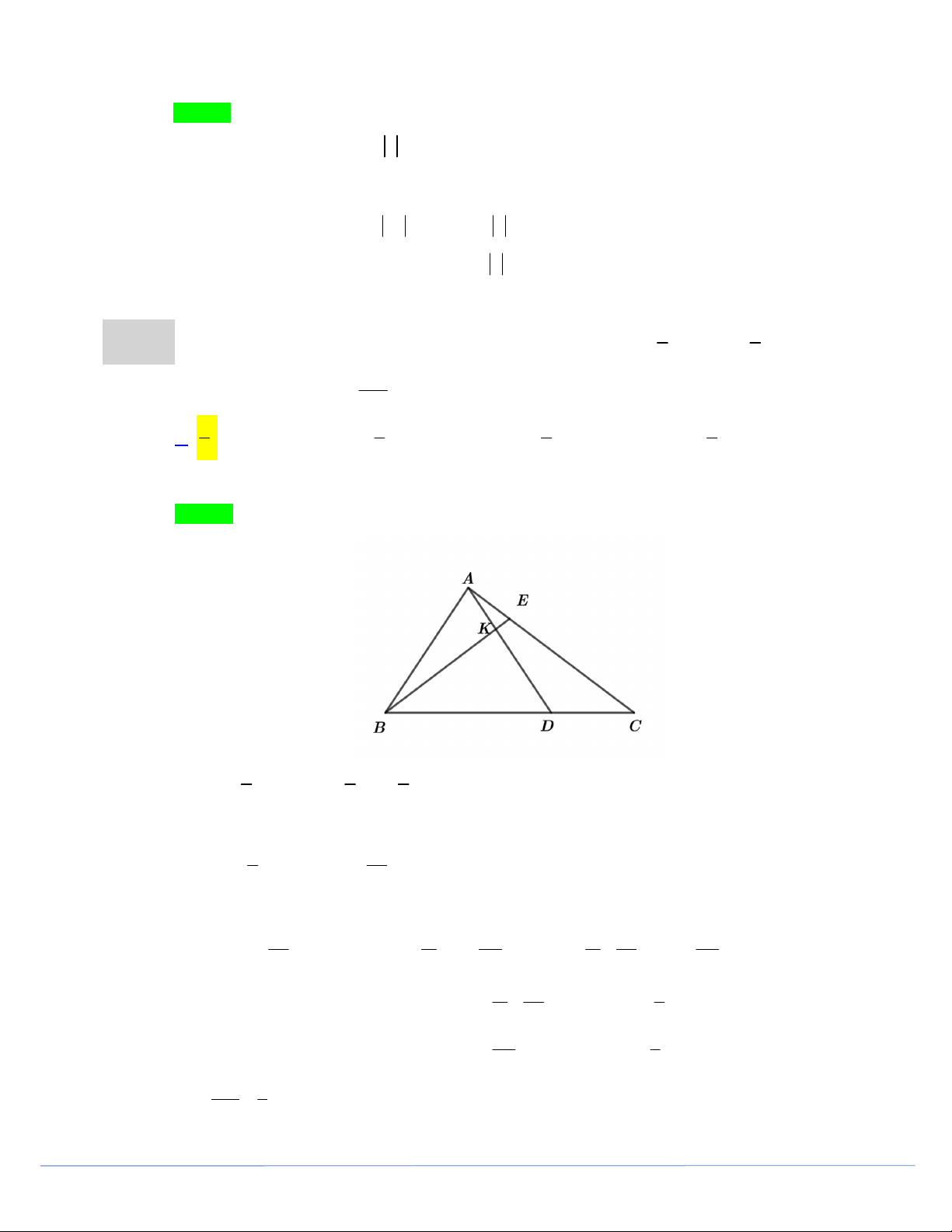
Câu 24. Cho tam giác ABC . Gọi D, E lần lượt là các điểm thỏa mãn: BD BC , AE AC . Gọi 3 4 AK
BE cắt AD tại K . Tỉ số bằng AD 1 2 3 1 A. . B. . C. . D. . 3 5 5 4
Câu 25. Cho tam giác ABC đều cạnh 3a . Lấy các điểm M , N lần lượt trên các cạnh BC,CA sao cho
BM a , CN  2a . Gọi P là điểm trên cạnh AB sao cho AM vuông góc PN . Độ dài PN theo a là Trang 5 a 21 a a 5 2a A. . B. . C. . D. . 5 3 3 5
II. PHẦN TỰ LUẬN (4 CÂU TỰ LUẬN – 5,0 ĐIỂM) Bài 26. Tìm
tập xác định các hàm số sau: 2x 1
2x 1  3x  2 a. y  . b. y  2 x x  6 x  2
Bài 27. Trong mặt phẳng tọa độ Oxy , cho ba điểm A3;  3 , B4; 2  , C  1  ;  1 .  
a. Tính tọa độ véc tơ AB , AC .    
b. Tìm tọa độ điểm M thỏa mãn MA 4MB MC  0
Câu 28. Xác định hàm số 2
y ax bx c biết đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ là
1; 2 và cắt trục tung tại điểm có tung độ bằng 2 . Lập bảng biến thiên và vẽ đồ thị của hàm số vừa tìm được.
Câu 29. Cho ABC có trọng tâm G , H là điểm đối xứng với B qua G . Gọi M là trung điểm đoạn
   
    
BC . Đặt AB b; AC c . Biểu thị các vectơ AH ;CH ; MH theo hai vectơ b;c . HẾT Trang 6 ĐÁP ÁN THAM KHẢO
ĐÁP ÁN PHẦN TRẮC NGHIỆM
1.C 2.B 3.D 4.D 5.A 6.B 7.B 8.C 9.B 10.D
11.A 12.D 13.C 14.B 15.D 16.B 17.A 18.D 19.B 20.B 21.C 22.C 23.D 24.A 25.A ĐÁP ÁN CHI TIẾT PHẦN TRẮC NGHIỆM Câu 1.
Trong các câu sau, câu nào là mệnh đề chứa biến?
A. 18 là số chính phương.
B. Hình chữ nhật có hai đường chéo bằng nhau. C.  2
x x5, x .
D. 9 là số nguyên tố. Lời giải Chọn C Câu 2.
Cho tập hợp A   ; a ; b ;
c d, phát biểu nào là sai?  ;ad  A  ;b c Ad  A
A. a A . B. . C. . D. . Lời giải Chọn B Câu 3.
Cho tập hợp A   5;
 3 . Tập C A là   ;  5   5; 3;  ;  5   3; A. . B. . C. . D. . Lời giải Chọn D x Câu 4.
Tìm tập xác định hàm số y  . x 1
A. 1; . B. 1; . C.   ;1  . D.   ;1  . Lời giải Chọn D Trang 7
Điều kiện x 1  0  x 1.
Vậy D    ;1 . Câu 5. Cho hàm số 2
y  2x x 1. Đỉnh của P là A.  1 7        I ;   . B. 1 11 I  ;   . C. 1 I ;1   . D. 1 I  ; 2   .  4 8   4 8   2   2  Lời giải Chọn A b 1 1
Đỉnh P là x   thế x  vào 2
y  2x x 1. 2a 4 4 7   Ta được y  1 7  I  ;   . 8  4 8  Câu 6.
Điều kiện nào để khi bình phương 2 vế phương trình sau ta được một phương trình tương đương: 2
x  4x  6  x  2 .
A. x   . B. x  2 . C. x  2 . D. x  2  . Lời giải Chọn B 2
x  4x  6  0  x   Điều kiện    x  2  0 x  2 Vậy x  2 . Câu 7.
Nghiệm của phương trình x x 1  0 là A. x  0. B. x 1. C. x 2. D. x 1  . Lời giải Chọn B Điều kiện: x 1
x x 1  0  x 1  0  x 1 0  x 1  Câu 8.
Số các vectơ (khác 0) có điểm đầu và điểm cuối là các đỉnh của hình vuông ABCD . A. 10. B. 11. C. 12. D. 13. Lời giải Chọn C
Cách 1: Có 6 đoạn thẳng nối từ các đỉnh của hình vuông ABCD , mà mỗi đoạn thẳng tạo
thành hai vectơ nên lập được 12 vectơ.
Cách 2: cố định 1 điểm làm gốc thì có 3 vectơ là lấy 3 điểm còn lại làm ngọn. Do vai trò của
4 điểm như nhau nên có 4.3 12 vectơ. Câu 9.
Chọn khẳng định đúng trong các hệ thức sau:
  
  
  
  
A. AB AC BC .
B. MP NM NP . C. CA BA CB .
D. AA BB AB . Lời giải Trang 8 Chọn B
  
    
Cách 1: Theo quy tắc trừ ta có: MP NM NP MP NP NM MP MP (đúng).
  
 
   
Cách 2: VT MN NP NM  MN NM   NP  0  NP NP VP   
Câu 10. Cho đoạn thẳng AB , hình nào sau đây biểu diễn đúng điểm M thỏa mãn: MA  4MB  0 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. Lời giải Chọn D     
Ta có MA  4MB  0  MA  4MB .  
Do đó MA  4.MA ; MA và MB ngược hướng.      
Câu 11. Cho u  (2;b), v   3;  1 , w   ;
a 5 . Vectơ w u v nếu:
A. a  5; b  6 .
B. a  5; b  3  .
C. a  4; b  4  .
D. a  3; b  4 . Lời giải Chọn A    a  2  3 a  5
Ta có: w u v     . 5   b  ( 1  ) b   6   
Câu 12. Cho a và b là hai vectơ khác vectơ 0 . Chọn đáp án đúng trong các đáp án sau:   
A. Tích vô hướng của a và b là một véc tơ khác vectơ 0 .  
B. Tích vô hướng của a và b là một số khác 0.  
C. Tích vô hướng của a và b là một số bằng 0.  
D. Tích vô hướng của a và b là một số thực. Lời giải Chọn D  
Tích vô hướng của a và b là một số thực.
Câu 13. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai?
A. Tam giác ABC cân thì tam giác có hai cạnh bằng nhau.
B. Số thực a chia hết cho 6 thì a chia hết cho 2 và 3 .
C. Tứ giác ABCD là hình bình hành thì AB song song với CD .
D. Tứ giác ABCD là hình chữ nhật thì tứ giác có ba góc vuông. Lời giải Chọn C Trang 9
Vì nếu tứ giác ABCD có AB song song với CD thì tứ giác có thể là hình thang không là hình bình hành.
Câu 14. Cho tập hợp A  1;2;4; 
6 . Có tất cả bao nhiêu tập hợp con của A có chứa phần tử 1? A. 9. B. 8 . C. 6 . D. 7 . Lời giải Chọn B
Số tập con của tập hợp 2;4; 
6 là 8 . Lấy mỗi tập con đó và thêm vào phần tử 1 ta được tập
con của tập hợp A  1;2;4;  6 thỏa mãn đề bài.
Vậy có tất cả 8 tập con thỏa mãn đề bài.
Câu 15. Cho hai tập hợp A   2; 
3, B  1; . Khi đó C bằng
  A B A. 1;3. B.  
;1  3;. C. 3;. D. ;2. Lời giải Chọn D
Ta có: AB   2;    C
C AB   ;  2  .  
  A B   \  AB
Câu 16. Cho hàm số bậc 2 có BBT sau:
Trong các hàm số sau, hàm số nào có BBT như trên? A. 2
y x  2x  3. B. 2
y  x  2x 1. C. 2
y  x  2x  5 . D. 2
y  x  2x  2 Lời giải Chọn B Câu 17. Cho hàm số 2
y ax bx c có đồ thị như hình vẽ Xác định các hệ số , a , b c
A. a  1,b  2, c  2 B. a  1,b  2, c  2 C. a  1,b  2, c  1 D. a  1,b  2, c  0 Trang 10 Lời giải Chọn A
Vì đồ thị hàm số cắt trục Ox tại điểm có tung độ là 2 nên c  2  .
Mặt khác đồ thị hàm số nhận điểm
I (1; 1) làm đỉnh nên  b  1 a  0  b   2  a b   2 2  a a  a  1        a  1    (vì c  2  và a  0 ) 2 2  b
  4ac  4a
4a  8a  4a b    2   1  b    2  a  4a
Vậy a  1,b  2, c  2
Dựa vào BBT ta thấy đồ thị hàm số nhận điểm I(1;2) làm đỉnh và có hệ số a  0 nên ta chọn hàm số 2
y  x  2x 1.
Câu 18 . Trong mặt phẳng Oxy , cho ba điểm Am 1;2, B2;5  2m,C m 3;4 . Tính giá trị của
tham số m để ba điểm ,
A B,C thẳng hàng . A. m  3 . B. m  2  . C. m  1. D. m  2 . Lời giải Chọn D   Ta có AB  3 ;
m 3 2m, AC   2  ;2   3  m 3  2m Ba điểm ,
A B,C thẳng hàng AB và AC cùng phương    m  2 . 2  2   
Câu 19. Tam giác ABC có AB AC a và BAC 120 . Tính AB AC .       a  
A. AB AC a 3.
B. AB AC  . a
C. AB AC  .
D. AB AC  2 . a 2 Lời giải Chọn B
Gọi M là trung điểm BC   AM BC. a
Trong tam giác vuông AMB , ta có  0 AM  . AB sin ABM  . a sin 30  . 2 A B M C   
Ta có AB AC  2AM  2AM  . a 
Câu 20. Cho lục giác đều ABCDEF tâm .
O Số các vectơ khác vectơ - không, cùng phương với OC có
điểm đầu và điểm cuối là các đỉnh của lục giác là A. 4. B. 6. C. 7. D. 9. Lời giải Trang 11 Chọn B
     
Đó là các vectơ: AB, B ,
A DE, ED, FC, CF .
Câu 21. Cho hai tập hợp M  2m 1;2m  
5 và N  m 1;m  7. Số các giá trị nguyên của tham số
m sao cho M N   là A. 10 . B. 11. C. 12 . D. 13 . Lời giải Chọn C
2m  5  m 1 m  4 
Xét M N      . 2m 1 m 7       m  8
Suy ra M N    4   m  8 .
Vậy có 12 giá trị m nguyên.    
Câu 22. Cho tam giác ABC , điểm I thỏa mãn 2IA  5IB  3IC  0 , điểm K thỏa mãn  
AK x AB; x   . Xác định x để ba điểm C ; K ; I thẳng hàng. 1 2 5 3 A. . B. . C. . D. . 3 3 7 7 Lời giải Chọn C  2  5 
Ta có CI IA IB . 3 3      
Theo giả thiết AK x AB IK IA xIB IA .   
IK  1 xIAxIB .  
Ba điểm C ; K ; I thẳng hàng  IK ;CI cùng phương. 1 x x      x 5 5 1
 2x x  . 2 5 7 3 3
Câu 23. Trong các hàm số sau, hàm số nào là hàm số chẵn? 2 x 1 A. y  .
B. y x 1 .
C. y x x . D. 2
y x  2 x  2 . x 1 Trang 12 Lời giải Chọn D
Xét hàm số y f x 2
x  2 x  2 có tập xác định D   . Suy ra x
   x    1 .
Mặt khác, f x  x2 2
 2 x  2  x  2 x  2  f x 2 . Từ  
1 ,2 suy ra hàm số y f x 2
x  2 x  2 là hàm số chẵn.  2   1 
Câu 24. Cho tam giác ABC . Gọi D, E lần lượt là các điểm thỏa mãn: BD BC , AE AC . Gọi 3 4 AK
BE cắt AD tại K . Tỉ số bằng AD 1 2 3 1 A. . B. . C. . D. . 3 5 5 4 Lời giải Chọn A  1   1  3 
Vì AE AC BE BC BA   1 . 4 4 4      Giả sử AK  .
x AD BK  .
x BD  1 x.BA .  2   2x  
Mà BD BC nên BK
.BC  1 x.BA. 3 3  
Vì B, K , E thẳng hàng B E nên có m sao cho BK  . m BE . 2x  
m  3m 
m 2x    3m    Do đó ta có:
.BC  1 x.BA BC BA . Hay  BC
x 1 BA  0     . 3 4 4  4 3   4  m 2x  8     0 m     
Do BC, BA không cùng phương nên ta có: 4 3 9    . 3m 1   x 1  0 x   4  3 AK 1 Vậy  . AD 3 Trang 13
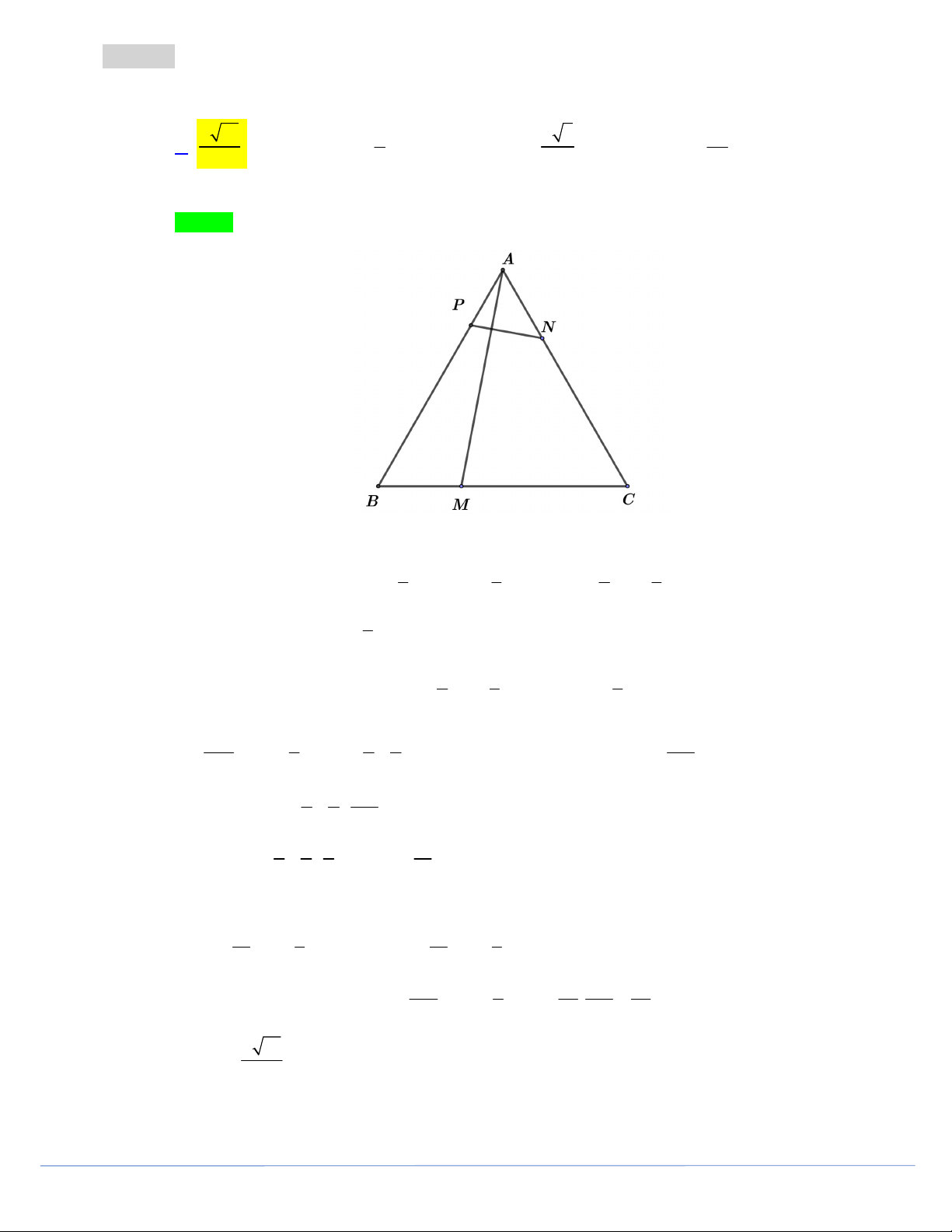
Câu 25. Cho tam giác ABC đều cạnh 3a . Lấy các điểm M , N lần lượt trên các cạnh BC,CA sao cho
BM a , CN  2a . Gọi P là điểm trên cạnh AB sao cho AM vuông góc PN . Độ dài PN theo a là a 21 a a 5 2a A. . B. . C. . D. . 5 3 3 5 Lời giải Chọn A   Đặt AP  .
x AB x  0 .
    1   1   2  1 
Ta có: AM AB BM AB BC AB   AC AB  AB AC . 3 3 3 3
    1 
PN PA AN   .
x AB AC . 3  
 2  1   
 1  
Do AM PN nên: AM .PN  0 
AB AC .  .
x AB AC  0      3 3   3  2 2x 1
 2 x         9a 2 2 2 
(3a)  (3a)   . AB AC  0    .
AB AC  9a cos 60   3 9  9 3   2  2  2 x  9a 2 2
 6xa a    0    9 3  2  2 x  9 4  6x 1   0  x     9 3  2 15 Khi đó: 2  4  1 
 4  1  2  PN  
.AB AC PN   .AB AC   15 3  15 3  2 16 1 8 9a 21 2 2 2 
(3a)  (3a)  .  a 225 9 45 2 25 a 21  PN  . 5 Trang 14 PHẦN TỰ LUẬN Bài 26. Tìm
tập xác định các hàm số sau: 2x 1
2x 1  3x  2 a. y  . b. y  2 x x  6 x  2 Lời giải x  2
a. Điều kiện xác định: 2
x x  6  0   . x  3 
Vậy D   \2;  3 .  1 x   2x 1 0 2   1   2  x
b. Điều kiện xác định: 3
x  2  0  x    2 .  3 x  2  0    x  2 x  2 
Vậy tập xác định của hàm số là 1  D  ; \     2 .  2 
Bài 27. Trong mặt phẳng tọa độ Oxy , cho ba điểm A3;  3 , B4; 2  , C  1  ;  1 .  
a. Tính tọa độ véc tơ AB , AC .    
b. Tìm tọa độ điểm M thỏa mãn MA 4MB MC  0 Lời giải  
a. Ta có AB1; 5   , AC 4;  4   . 
   3
  x  4  x    x   x  5 M
4 M   1 M  0
b. Ta có MA 4MB MC  0   M   3
  y  4   y    y   y  1  M
 2 M   1 M  0  M
Vậy điểm M 5;  1 .
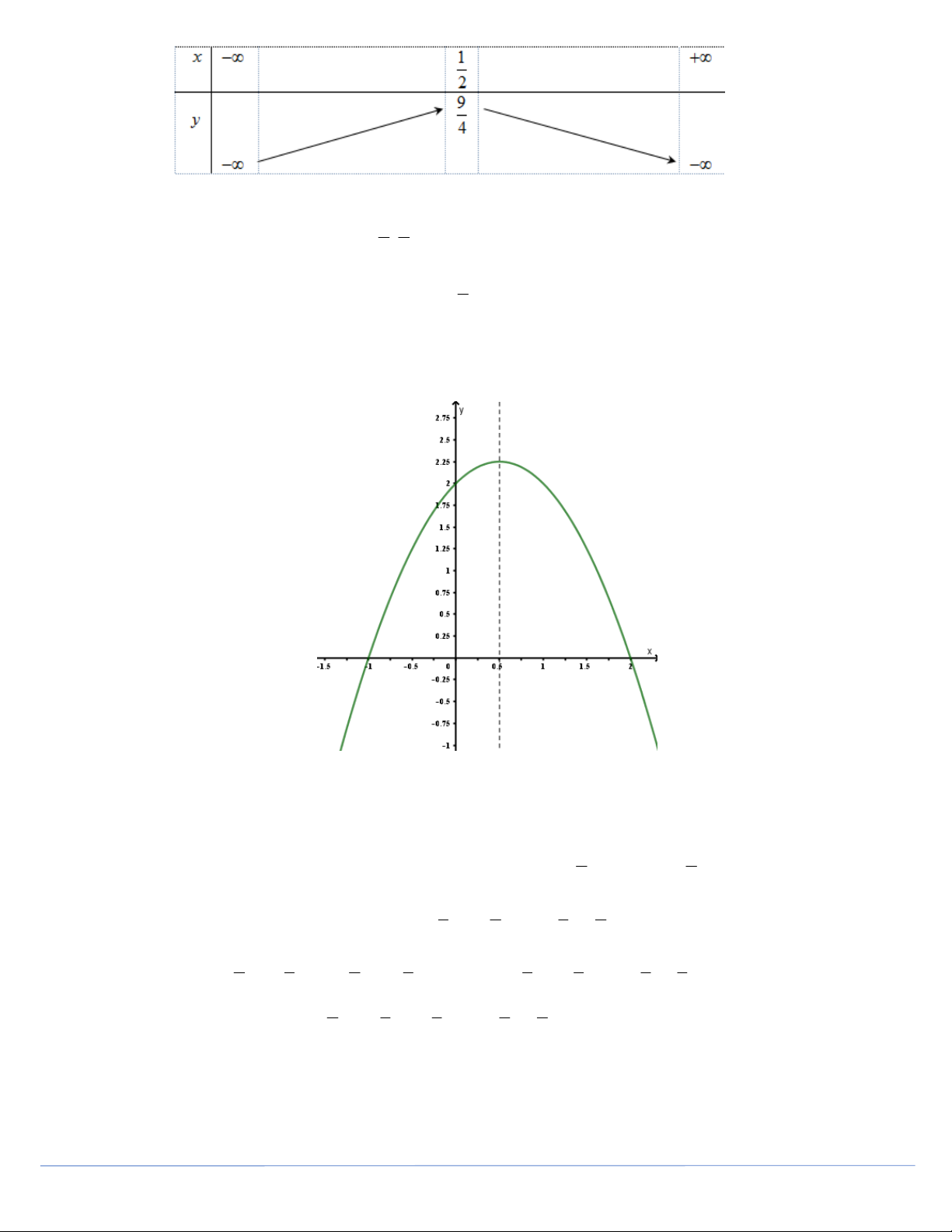
Câu 28. Xác định hàm số 2
y ax bx c biết đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ là
1; 2 và cắt trục tung tại điểm có tung độ bằng 2 . Lập bảng biến thiên và vẽ đồ thị của hàm số vừa tìm được. Lời giải
a b c  0 a  1   
+ Theo bài ra ta có: 4a  2b c  0  b  1 . c 2   c  2    Hàm số cần tìm là: 2
y  x x  2. + Bảng biến thiên: Trang 15 + Vẽ đồ thị hàm số:  1 9 
Đồ thị hàm số có: + Đỉnh I ;   .  2 4  1
+ Trục đối xứng: x  . 2
+ Giao với trục hoành:  1;  0;2;0.
+ Giao với trục tung: 0;2 .
Câu 29. Cho ABC có trọng tâm G , H là điểm đối xứng với B qua G . Gọi M là trung điểm đoạn
   
     BC . Đặt ;
AB b AC c . Biểu thị các vectơ AH ;CH ; MH theo hai vectơ b;c . Lời giải        4 
 2  
+ Ta có: AH AB  2AG AH   AB  2AG   AB AM   AB   AB AC 3 3 1  2  1  2 
  AB AC   b c 3 3 3 3  2  1 
2  1   1  1  1  1 
+ CH CA CB   AC   AB AC   AB AC   b c . 3 3 3 3 3 3 3 3
  
1  1  1  5  1  +
MH MC CH BC AB AC   b c . 2 3 3 6 6 HẾT Trang 16