Đề kiểm tra giữa kỳ 1 Toán 10 năm 2019 – 2020 trường Lý Thái Tổ – Bắc Ninh

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH ĐỀ KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC 2019 - 2020
TRƯỜNG THPT LÝ THÁI TỔ Môn thi: TOÁN 10
Thời gian làm bài: 90 phút (không kể thời gian giao đề). ĐỀ CHÍNH THỨC
Ngày kiểm tra: 25 tháng 10 năm 2019
Câu 1 (2,0 điểm). Tìm tập xác định của các hàm số: 3x  2019 a) y  . x  2 b) y 
9  3x  2  x .
Câu 2 (2,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị (P)của hàm số 2
y  x  2x  3. Câu 3 (2,0 điểm).
a) Tìm tất cả các giá trị của tham số m để hai đường thẳng 2
d : y  m x  2m  3 và
d ' : y  3 2mx 1 song song với nhau.
b) Biết đồ thị hàm số 2
y  ax bx  c có đỉnh là I 1;8 và đi qua điểm C 0;5. Tính tổng 2 2 2
S  a b  c . Câu 4 (3,0 điểm). 
   
Cho tam giác ABC . Gọi M, N, P là các điểm thỏa mãn MA  2MB, NA  NC  0,   
2PB  PC  0.
    
a) Biểu diễn AM, AN, AP theo AB, AC.
b) Chứng minh M, N, P thẳng hàng. Câu 5 (1,0 điểm).
a) Tìm tất cả giá trị của tham số m để hàm số y  m   2 2
2 x  4mx  m m  2 là hàm số lẻ.
b) Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  x x   2
2 x  2x  4 trên đoạn  2;2  .  
---------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ........................................................... Số báo danh: .................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH
ĐÁP ÁN – THANG ĐIỂM
TRƯỜNG THPT LÝ THÁI TỔ
ĐỀ THI GIỮA HỌC KÌ I NĂM 2019 - 2020
Môn thi: TOÁN; Khối 10
(Đáp án – thang điểm gồm 03 trang) Câu Ý Nội dung trình bày Điểm 1 2,0
a Điều kiện xác định: x − 2 ≠ 0 ⇔ x ≠ 2 0,5
Vậy tập xác định của hàm số là D = R \{ } 2 0,5
b Điều kiện xác định: 9  − 3x ≥ 0  0,25 2 + x ≥ 0 x ≤ 3 ⇔  ⇔ 2 − ≤ x ≤ 3 0,5 x ≥ 2 −
Vậy tập xác định của hàm số là D = [ 2; − ]3 0,25 2 Cho hàm số 2
y = x − 2x − 3 2,0
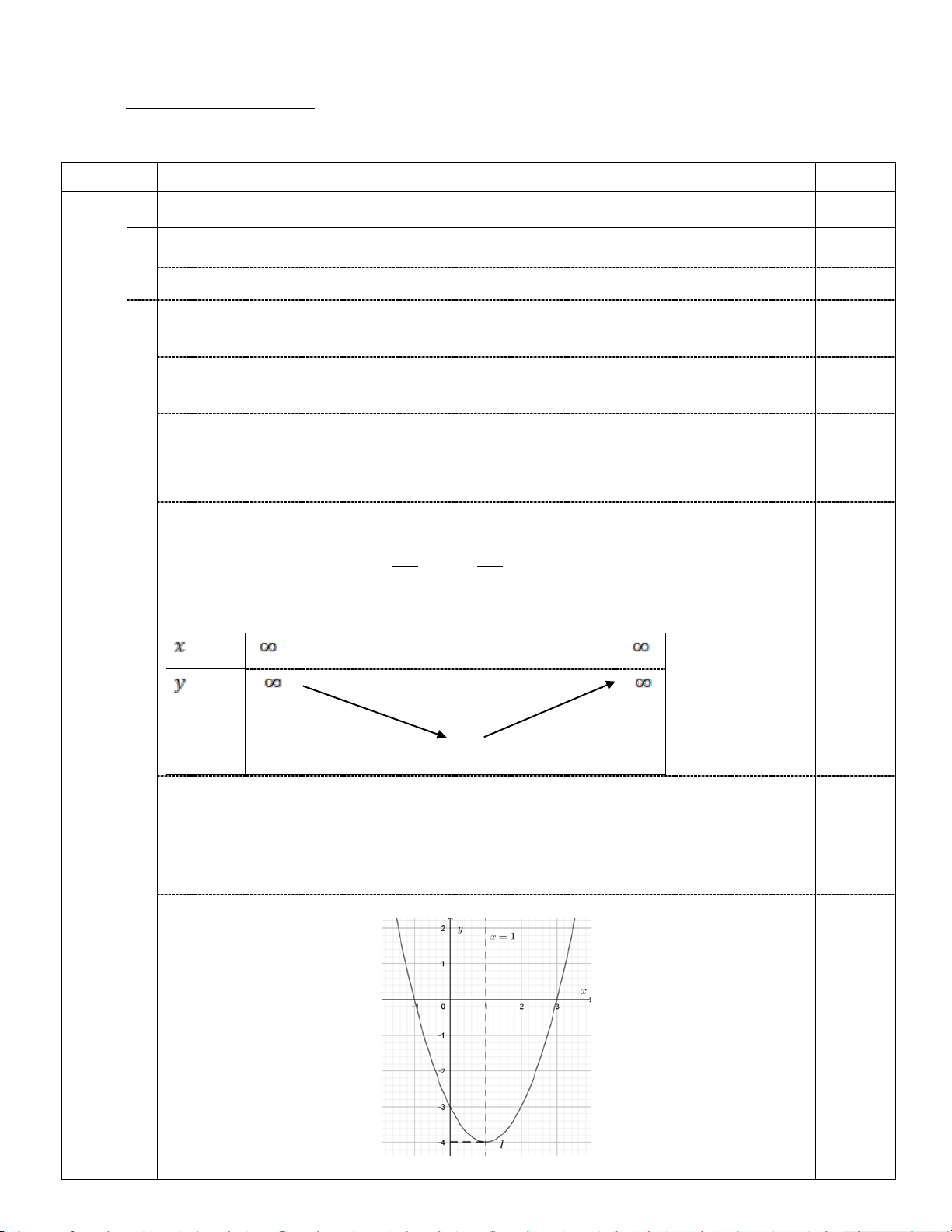
Khảo sát sự biến thiên và vẽ đồ thị (P) của hàm số. * TXĐ: R ∆ * Bảng biến thiên b : Ta có: − =1, − = 4
− . Vì a =1 > 0 nên 2a 4a
Hàm số đồng biến trong (1;+∞) ; nghịch biến trong ( ; −∞ ) 1 . 1,0 - 1 + + + -4 Đồ thị : - Đỉnh I(1;-4)
- Trục đối xứng: đường thẳng x = 1. 0,5
- Giao của đồ thị với trục Oy : (0;-3) .
- Giao của đồ thị với trục Ox : (-1;0) ;(3;0). Vẽ đồ thị 0,5 1 3
a Tìm m để d , d ' song song với nhau… 1,0 2  =  = − Hai đường thẳng a a ' m 3 2m
d , d ' song song ⇔  ⇔  0,5 b  ≠ b' 2m − 3 ≠ 1 − 2
m + 2m − 3 = 0 m =1∨ m = 3 − ⇔  ⇔  ⇔ m = 3 − m ≠ 1 m ≠ 1 0,5 Vậy m = 3
− là giá trị cần tìm.
b Biết đồ thị hàm số 2
y  ax bx  c có đỉnh là I 1;8 và đi qua điểm 1,0
C 0;5. Tính tổng 2 2 2
S  a b  c . b
Vì đồ thị có đỉnh là I 1; 8 nên ta có −
= 1;a + b + c = 8 0,25 2a
Đồ thị đi qua C 0;5 nên c = 5 0,25
Từ đó suy ra a  3,b  6,c  5 0,5
Vậy S  a b c   2 2 2 2 2 2 3  6  5  70
     4
a Biểu diễn AM,AN,AP theo AB,AC. 1,5       
Có MA  2MB  AM 
 2AB AM  AM  2AB 0,5   
     1 
NA  NC  0  AN 
 AC  AN  0  AN  AC 2 0,5           
PB  PC   AB AP 2 1 2 0 2
 AC  AP  0  AP  AB  AC 3 3 0,5
b Chứng minh M, N, P thẳng hàng. 1,5    1    1 
MN  AN  AM  AC  2AB  2AB  AC (1) 2 2    1,0 2  1   4  1 
MP  AP  AM  AB  AC  2AB   AB  AC (2) 3 3 3 3     Từ (1) và (2) 3
 MN  MP  MN,MP cùng phương nên M,N,P thẳng 2 0,5 hàng. 5 a Tìm
tất cả giá trị của tham số m để hàm số
y  f x  m   2 2
2 x  4mx  m m  2 0,5 là hàm số lẻ.
Tập xác định D   là tập đối xứng.
Để hàm số đã cho là hàm số lẻ  f  x
   f x, x  .  0,25  m   2 x   2 2 2
2 m  m   2  0, x  .  2 2
 m 2  0    m  2   2 2 m  m   2  0 0,25 
Vậy m  2 là giá trị cần tìm.
b Tìm giá trị nhỏ nhất và lớn nhất của hàm số y  x x   2
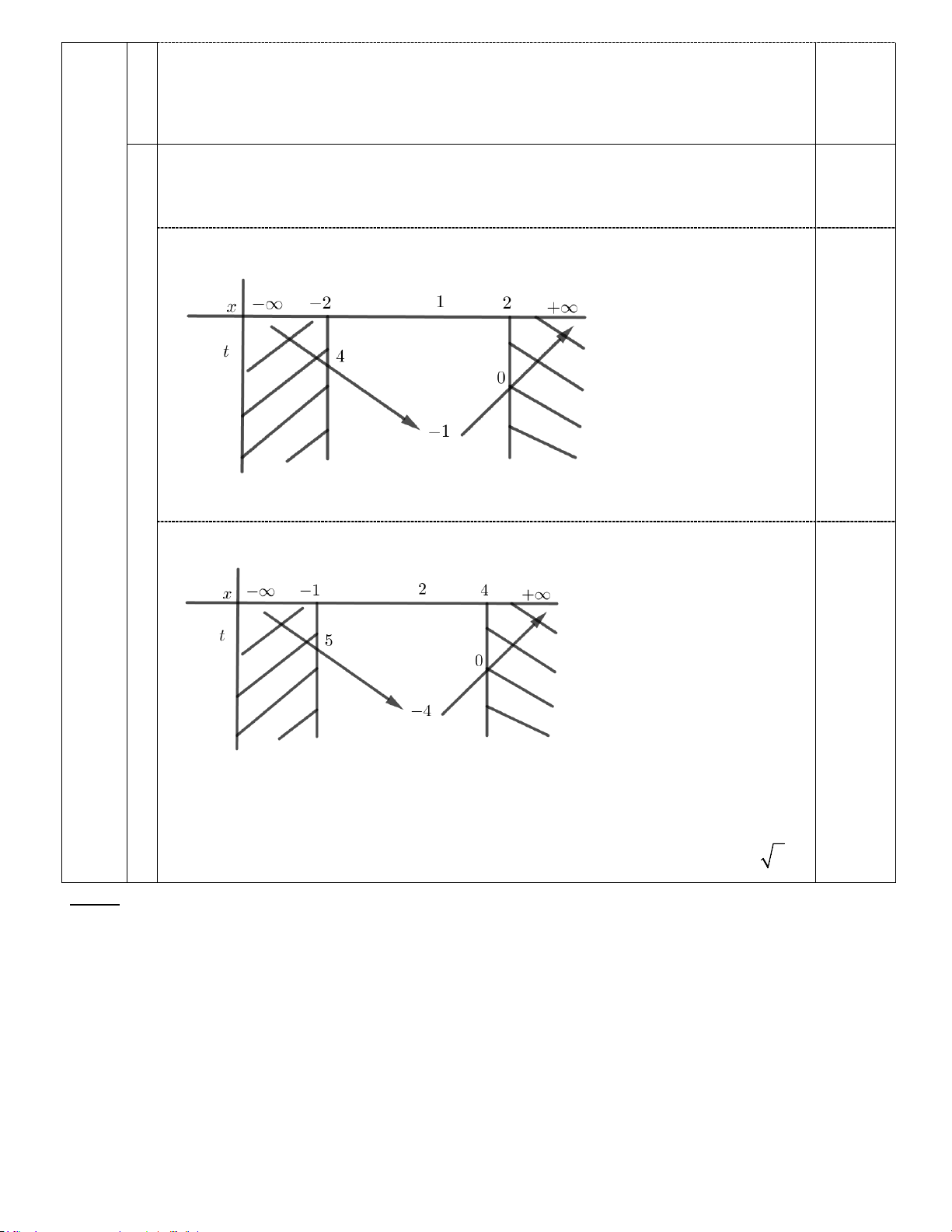
2 x  2x  4 trên đoạn 0,5  2;2    Đặt 2
t  x  2x với x  2;2   
 ta có bảng biến thiên 0,25 Từ đó suy r  a t   1; 4   . Khi đó hàm số 2
y  t  4t với t  1;4   
 . Ta có bảng biến thiên: 0,25
Từ BBT, trên đoạn  1;4    ta có:
Giá trị lớn nhất y  5
t    x  LN khi 1 1
và giá trị nhỏ nhất là: y  4 2
t  2  x  2x  2  x  1  3 NN khi
Chú ý: Mọi cách giải khác nếu đúng vẫn cho điểm tối đa U U 3
Document Outline

• ĐỀ TOÁN 10
• ĐÁP-ÁN-TOÁN-10-NAM-HOC-2019-2020