Đề kiểm tra giữa kỳ môn xác suất thống kê toa201.3 - đáp án 2023 môn Xác suất thống kê| Đại học Duy Tân

21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu KHOA CƠ BẢN
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ BỘ MÔN TOÁN TOA201.3(tháng 6/2022)
Thời gian: 50 phút (không được sử dụng tài liệu) Điểm
Họ và tên:…………………………………………………
Lớp:……………………… STT:…………………………
Chú ý: Thí sinh lựa chọn A, B, C, D điền vào ô trả lời tương ứng. Nếu có kết quả
khác các phương án trong đề, thí sinh ghi rõ kết quả đó thay vì ghi A, B, C, D. Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 TL
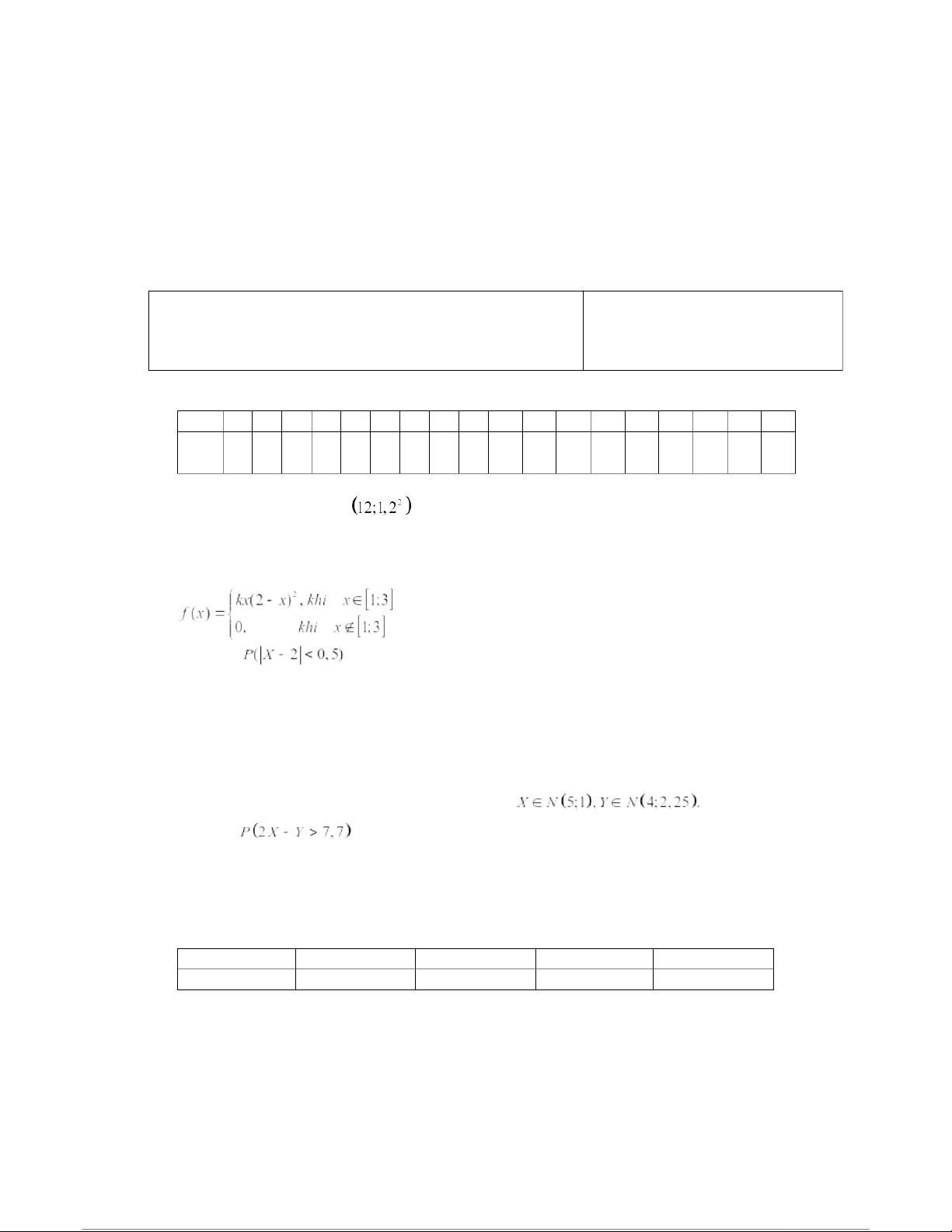
Câu 1. Độ dài chi tiết (tính bằng cm) do một máy tự động sản xuất ra là biến ngẫu nhiên phân phối chuẩn N
. Xác suất để lấy ngẫu nhiên ra 3 chi tiết thì được
đúng 2 chi tiết có kích thước từ 10,5 cm đến 15 cm là: A. 0,4838 B. 0,1464 C. 0,2646 D. 0,3252
Câu 2. Cho hàm mật độ xác suất của biến ngẫu nhiên X có dạng Xác suất bằng A. 1/2 B. 1/4 C. 1/6 D. 1/8
Câu 3. Với đầu bài câu 2, E(X) bằng A. 2,7 B. 2,5 C. 2,3 D. 2,1
Câu 4. Bốn người khách ra khỏi nhà bỏ quên mũ. Chủ nhà không biết rõ chủ của
những chiếc mũ đó nên gửi trả cho họ một cách ngẫu nhiên. Xác suất để có ít nhất một
người được trả đúng mũ là A. 0,385 B. 0,465 C. 0,545 D. 0,625
Câu 5. Cho hai biến ngẫu nhiên độc lập X, Y và Khi đó xác suất bằng A. 0,2358 B. 0,2483 C. 0,2514 D. 0,2611
Câu 6. Trong một đợt phát hành xổ số, xác suất để mua được vé trúng thưởng là 0,15.
Cần phải mua ít nhất bao nhiêu vé để với xác suất lớn hơn 0,94 ta sẽ trúng ít nhất 1 vé A. 18 B. 20 C. 21 D. 24
Câu 7. Cho biến ngẫu nhiên rời rạc có bảng phân phối xác suất như sau X -3 -1 2 4 P 0,25 0,15 P 0,45 V(X) bằng A. 5,43 B. 6,54 C. 7,65 D. 8,76
Câu 8. Có 15 hộp bi, trong đó có 6 hộp loại I, mỗi hộp có 7 bi trắng và 3 bi đỏ; 4 hộp
loại II, mỗi hộp có 7 bi trắng, 5 bi đỏ; 5 hộp loại III, mỗi hộp có 6 bi trắng, 9 bi đỏ.
Lấy ngẫu nhiên ra một hộp, rồi từ hộp đó lấy ngẫu nhiên ra 2 bi. Xác suất để lấy được hai bi đỏ là A. 0,1814 B. 0,1619 C. 0,1512 D. 0,1715 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu
Câu 9. Với đầu bài câu 8, biết rằng hai bi lấy ra là hai bi đỏ. Xác suất để hai bi đó
thuộc hộp loại I là A. 0,176 B. 0,165 C. 0,155 D. 0,147
Câu 10. Cho hai biến ngẫu nhiên độc lập X, Y và bằng A. 0,01 B. 0,025 C. 0,05 D. 0,1
Câu 11. Tung hai con xúc xắc đối xứng và đồng chất trên mặt phẳng. Gọi X là tổng số
chấm xuất hiện ở mặt trên của hai con xúc xắc đó. F(x) là hàm phân bố xác suất của
X; F(x) = + m khi 10 < x 11. Giá trị của m bằng A. 2/3 B. 1/2 C. 1/6 D. 3/4
Câu 12. Cho A và B là các biến cố sao cho P(A) = 3/5; P(B) = 1/11; P(A + B) = 4/11. Khi đó bằng A. 5/11 B. 6/11 C. 7/11 D. 8/11
Câu 13. Chiều dài của một loại cây là biến ngẫu nhiên X (đơn vị là m) có phân phối chuẩn N
. Biết rằng số cây có chiều dài thấp hơn 18 m chiếm tỷ lệ 3,92% và số
cây có chiều dài cao hơn 25,49 m chiếm tỷ lệ 4,09%. Giá trị của và bằng A. 21,7664; 2,14 B. 21,6447; 2,38 C. 21,5776; 2,46 D. 21,8335; 2,21
Câu 14. Chọn khẳng định đúng trong các khẳng định sau
A. P(A + B) = P(A) + P(B) khi và chỉ khi A, B là hai biến cố xung khắc
B. Nếu biến cố A kéo theo biến cố B thì P(A) < P(B) C. thì D.
độc lập thì A và B cũng độc lập
Câu 15. Độ dài của sản phẩm do 1 nhà máy sản xuất là biến ngẫu nhiên phân phối
chuẩn với kỳ vọng là 20 cm và độ lệch chuẩn là 0,5 cm. Lấy ngẫu nhiên 3 sản phẩm,
xác suất để được không quá 2 sản phẩm có độ dài nằm trong khoảng (18,5; 21,5) cm là A. 0,09965 B. 0,09979 C. 0,00778 D. 0,03989
Câu 16. Một máy tự động có tỷ lệ phế phẩm là 2%. Trong 400 sản phẩm do máy sản
xuất ra thì số chính phẩm có khả năng nhiều nhất là A. 396 hoặc 397 B. 392 hoặc 393 C. 392 D. 397
Câu 17. Tung một con xúc xắc cho tới khi được mặt chẵn chấm thì dừng. Xác suất để
người đó phải tung số chẵn lần là A. 6/33 B. 1/3 C. 3/56 D. 5/11
Câu 18. Một người góp x (ngàn đồng) tham gia một trò chơi như sau: Gieo đồng thời
2 con xúc xắc cân đối đồng chất, nếu được 2 mặt 6 chấm thì được 100 000đ; 1 mặt 6
chấm thì được 26 000đ. Giá trị của x để về trung bình người chơi hòa vốn là A. 10 B. 15 C. 17 D. 20
Hà Nội, ngày 01 tháng 06 năm 2022 GV giảng dạy
ThS. Phan Thị Hương 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu KHOA CƠ BẢN
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ BỘ MÔN TOÁN TOA201.3(Tháng 6/2022)
Thời gian: 50 phút (không được sử dụng tài liệu) Điểm
Họ và tên: ………………………………………………...
Lớp:……………………………STT:……………………..
Chú ý: Thí sinh lựa chọn A, B, C, D điền vào ô trả lời tương ứng. Nếu có kết quả
khác các phương án trong đề, thí sinh ghi rõ kết quả đó thay vì ghi A, B, C, D. Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 TL
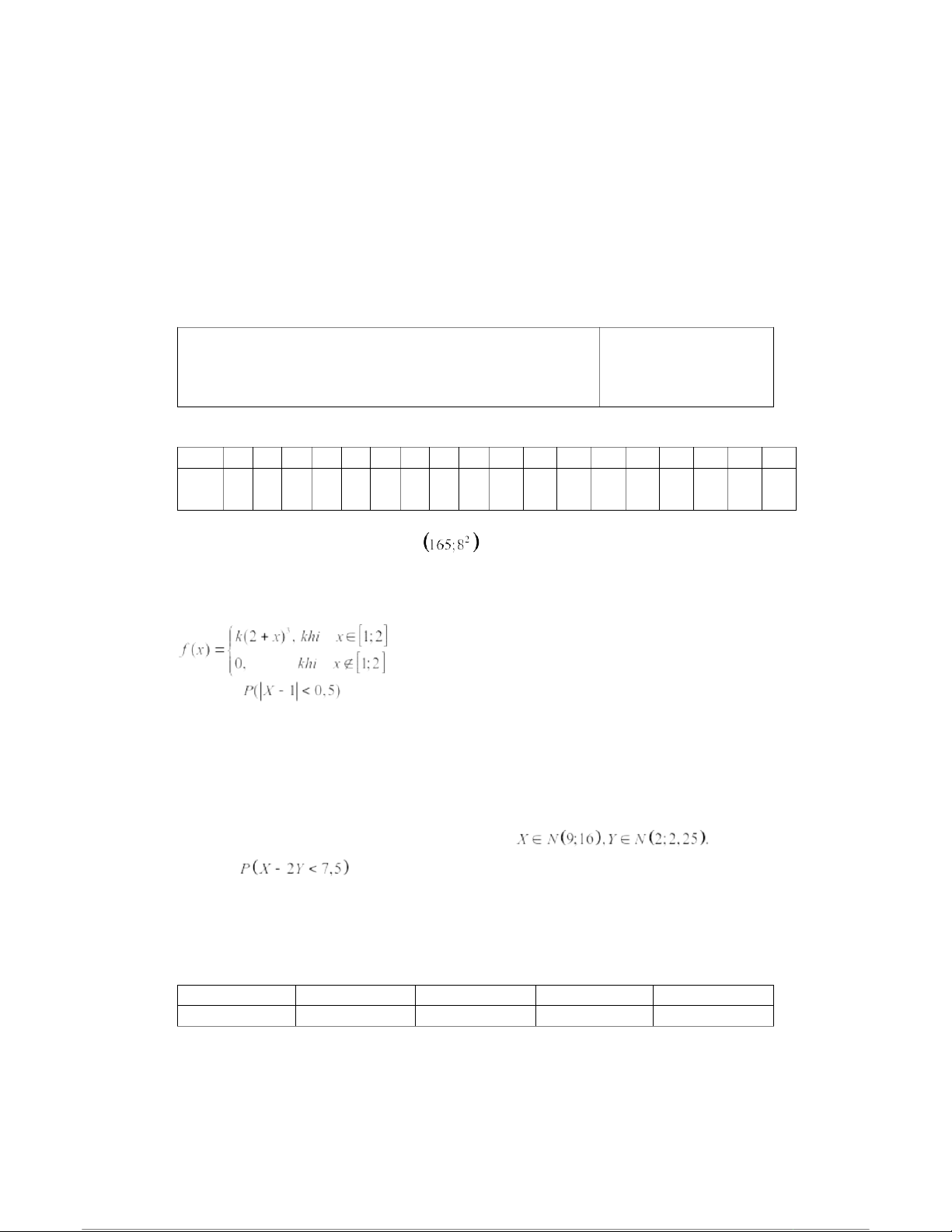
Câu 1. Chiều cao của nam giới trưởng thành (tính bằng cm) ở một vùng dân cư là
biến ngẫu nhiên phân phối chuẩn N
. Xác suất để lấy ngẫu nhiên 3 thanh niên
thì có đúng 2 thanh niên có chiều cao từ 163 cm đến 171 cm là: A. 0,2407 B. 0,2509 C. 0,2608 D. 0,2706
Câu 2. Cho hàm mật độ xác suất của biến ngẫu nhiên X có dạng Xác suất bằng A. 0,4121 B. 0,5232 C. 0,6343 D. 0,7454
Câu 3. Với đầu bài câu 2, E(X) bằng A. 1,5703 B. 1,4206 C. 1,3804 D. 1,6105
Câu 4. Một đoàn tàu gồm 3 toa đỗ ở sân ga. Có 4 hành khách mới bước lên tàu. Mỗi
hành khách độc lập với nhau chọn ngẫu nhiên một toa. Xác suất để mỗi toa có ít nhất
một hành khách mới bước lên là A. 1/16 B. 3/16 C. 9/16 D. 15/16
Câu 5. Cho hai biến ngẫu nhiên độc lập X, Y và Khi đó xác suất bằng A. 0,6368 B. 0,6517 C. 0,6736 D. 0,6915
Câu 6 .Tỷ lệ phế phẩm của một lô hàng là 1%. Cần phải lấy ít nhất bao nhiêu sản
phẩm từ lô hàng đó để với xác suất lớn hơn 0,95 được ít nhất 1 phế phẩm là A. 297 B. 298 C. 299 D. 296
Câu 7. Cho biến ngẫu nhiên rời rạc có bảng phân phối xác suất như sau X -5 -1 2 3 P 0,15 0,25 P 0,35 V(X) bằng A. 7,5962 B. 7,6184 C. 7,9253 D. 7,8475
Câu 8. Có 12 hộp bi, trong đó có 5 hộp loại I, mỗi hộp có 4 bi trắng và 5 bi đỏ; 3 hộp
loại II, mỗi hộp có 3 bi trắng, 9 bi đỏ; 4 hộp loại III, mỗi hộp có 8 bi trắng, 7 bi đỏ.
Lấy ngẫu nhiên ra một hộp, rồi từ hộp đó lấy ngẫu nhiên ra 2 bi. Xác suất để lấy được hai bi trắng là A. 0,4128 B. 0,3851 C. 0,2382 D. 0,1697 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu
Câu 9. Với đầu bài câu 8, biết rằng hai bi lấy ra là hai bi trắng. Xác suất để hai bi đó
thuộc hộp loại III là A. 0,3732 B. 0,2153 C. 0,5238 D. 0,2308
Câu 10. Cho hai biến ngẫu nhiên độc lập X, Y và bằng A. 0,9 B. 0,925 C. 0,95 D. 0,975
Câu 11. Tung hai con xúc xắc đối xứng và đồng chất trên mặt phẳng. Gọi X là tổng số
chấm xuất hiện ở mặt trên của hai con xúc xắc đó. F(x) là hàm phân bố xác suất của
X; F(x) = + m khi 11 < x 12. Giá trị của m bằng A. 23/36 B. 5/36 C. 17/36 D. 11/36
Câu 12. Cho A và B là các biến cố sao cho P(A) = 3/5; P(B) = 3/7; P(A + B) = 6/7. Khi đó bằng A. 3/7 B. 4/7 C. 2/7 D. 5/7
Câu 13. Thời gian đi từ nhà đến trường của một sinh viên A là một biến ngẫu nhiên X
(đơn vị là phút) có phân phối chuẩn N
. Biết rằng số ngày A đến trường mất ít
hơn 20 phút chiếm tỷ lệ 35,2% và số ngày A đến trường mất hơn 30 phút chiếm tỷ lệ
11,12%. Giá trị của và bằng A. 22,645; 5,58
B. 22,375; 6,25 C. 22,425; 6,45 D. 22,195; 6,65
Câu 14. Chọn khẳng định sai trong các khẳng định sau
A. P(A + B) = P(A) + P(B) suy ra A, B là hai biến cố xung khắc
B. Nếu biến cố A kéo theo biến cố B thì P(A) P(B) C.
thì với n không đổi, phương sai của nó lớn nhất khi p = 1/2 D. độc lập thì cũng độc lập
Câu 15. Trọng lượng của sản phẩm là biến ngẫu nhiên phân phối chuẩn có E(X) = 3
kg. Biết P(2 < X < 4) = 0,62. Sản phẩm được coi là đạt tiêu chuẩn nếu trọng lượng của
nó lớn hơn 2 kg. Tỷ lệ phế phẩm là A. 0,1556 B. 0,1806 C. 0,1900 D. 0,1950
Câu 16. Một máy tự động có tỷ lệ phế phẩm là 5%. Trong 400 sản phẩm do máy sản
xuất ra thì số phế phẩm có khả năng nhiều nhất là A. 20 hoặc 21 B. 10 hoặc 11 C. 20 D. 19
Câu 17. Tung một con xúc xắc cho tới khi được mặt chẵn chấm thì dừng. Xác suất để
người đó phải tung số lẻ lần là A. 6/11 B. 2/3 C. 6/33 D. 5/11
Câu 18. Một người góp x (ngàn đồng) tham gia một trò chơi như sau: Gieo đồng thời
2 con xúc xắc cân đối đồng chất, nếu được 2 mặt cùng số chấm thì được thưởng 60
000đ; 2 mặt xuất hiện số chấm liên tiếp nhau thì được thưởng 36 000đ. Giá trị của x
để về trung bình người chơi hòa vốn là A. 10 B. 15 C. 17 D. 20
Hà Nội, ngày 01 tháng 06 năm 2022 GV giảng dạy
ThS. Phan Thị Hương 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu KHOA CƠ BẢN
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ BỘ MÔN TOÁN TOA201.3(tháng 6/2022)
Thời gian: 50 phút (không được sử dụng tài liệu) Điểm
Họ và tên: ………………………………………………...
Lớp:…………………………….. STT:…………………..
Chú ý: Thí sinh lựa chọn A, B, C, D điền vào ô trả lời tương ứng. Nếu có kết quả
khác các phương án trong đề, thí sinh ghi rõ kết quả đó thay vì ghi A, B, C, D. Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 TL
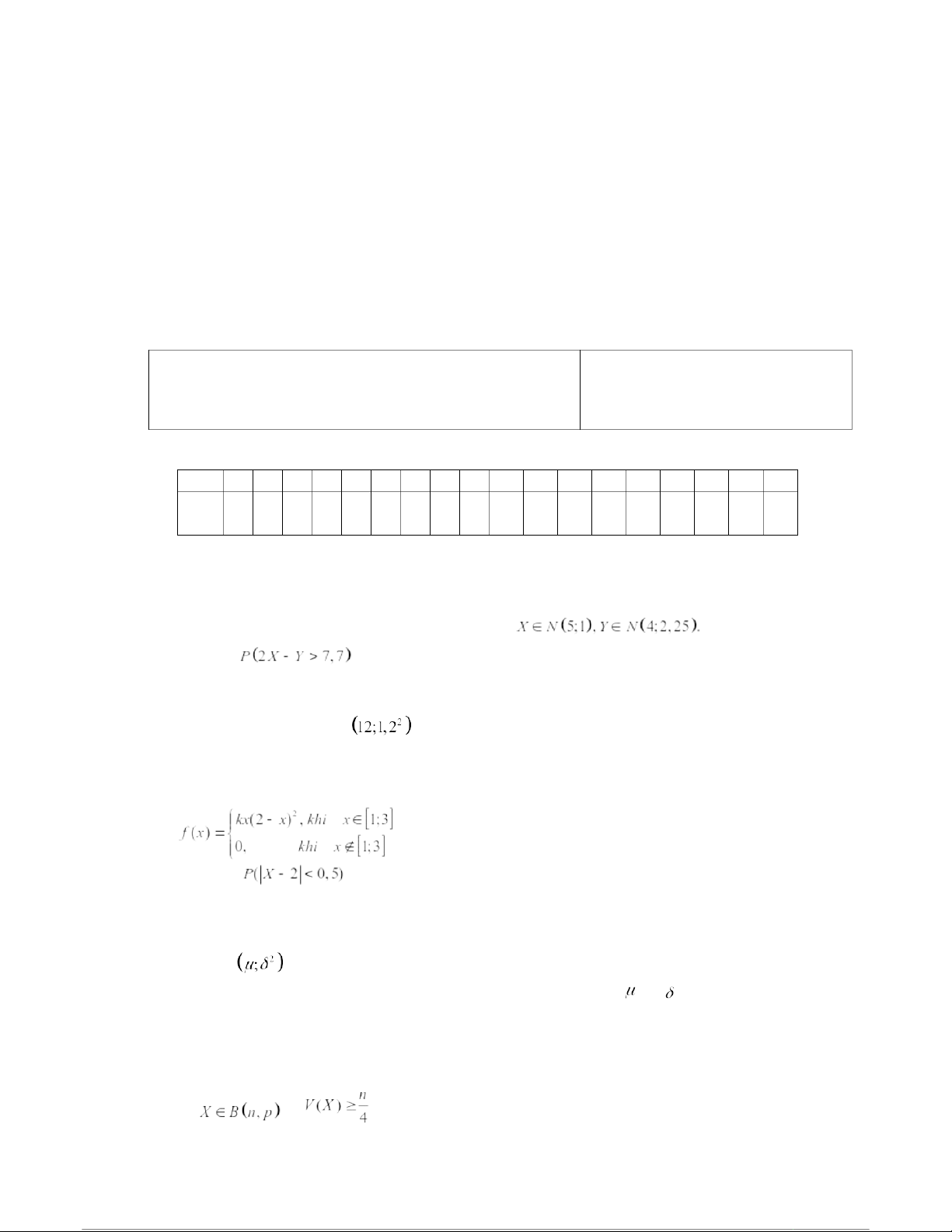
Câu 1. Bốn người khách ra khỏi nhà bỏ quên mũ. Chủ nhà không biết rõ chủ của
những chiếc mũ đó nên gửi trả cho họ một cách ngẫu nhiên. Xác suất để có ít nhất một
người được trả đúng mũ là A. 0,385 B. 0,465 C. 0,545 D. 0,625
Câu 2. Cho hai biến ngẫu nhiên độc lập X, Y và Khi đó xác suất bằng A. 0,2358 B. 0,2483 C. 0,2514 D. 0,2611
Câu 3. Độ dài chi tiết (tính bằng cm) do một máy tự động sản xuất ra là biến ngẫu nhiên phân phối chuẩn N
. Xác suất để lấy ngẫu nhiên ra 3 chi tiết thì được
đúng 2 chi tiết có kích thước từ 10,5 cm đến 15 cm là: A. 0,4838 B. 0,1464 C. 0,2646 D. 0,3252
Câu 4. Cho hàm mật độ xác suất của biến ngẫu nhiên X có dạng Xác suất bằng A. 1/2 B. 1/4 C. 1/6 D. 1/8
Câu 5. Với đầu bài câu 4, E(X) bằng A. 2,7 B. 2,5 C. 2,3 D. 2,1
Câu 6. Chiều dài của một loại cây là biến ngẫu nhiên X (đơn vị là m) có phân phối chuẩn N
. Biết rằng số cây có chiều dài thấp hơn 18 m chiếm tỷ lệ 3,92% và số
cây có chiều dài cao hơn 25,49 m chiếm tỷ lệ 4,09%. Giá trị của và bằng A. 21,7664; 2,14 B. 21,6447; 2,38 C. 21,5776; 2,46 D. 21,8335; 2,21
Câu 7. Chọn khẳng định đúng trong các khẳng định sau
A. P(A + B) = P(A) + P(B) khi và chỉ khi A, B là hai biến cố xung khắc
B. Nếu biến cố A kéo theo biến cố B thì P(A) < P(B) C. thì 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu D.
độc lập thì A và B cũng độc lập
Câu 8. Có 15 hộp bi, trong đó có 6 hộp loại I, mỗi hộp có 7 bi trắng và 3 bi đỏ; 4 hộp
loại II, mỗi hộp có 7 bi trắng, 5 bi đỏ; 5 hộp loại III, mỗi hộp có 6 bi trắng, 9 bi đỏ.
Lấy ngẫu nhiên ra một hộp, rồi từ hộp đó lấy ngẫu nhiên ra 2 bi. Xác suất để lấy được hai bi đỏ là A. 0,1814 B. 0,1619 C. 0,1512 D. 0,1715
Câu 9. Với đầu bài câu 8, biết rằng hai bi lấy ra là hai bi đỏ. Xác suất để hai bi đó
thuộc hộp loại I là A. 0,176 B. 0,165 C. 0,155 D. 0,147
Câu 10. Cho A và B là các biến cố sao cho P(A) = 3/5; P(B) = 1/11; P(A + B) = 4/11. Khi đó bằng A. 5/11 B. 6/11 C. 7/11 D. 8/11
Câu 11. Độ dài của sản phẩm do 1 nhà máy sản xuất là biến ngẫu nhiên phân phối
chuẩn với kỳ vọng là 20 cm và độ lệch chuẩn là 0,5 cm. Lấy ngẫu nhiên 3 sản phẩm,
xác suất để được không quá 2 sản phẩm có độ dài nằm trong khoảng (18,5; 21,5) cm là A. 0,09965 B. 0,09979 C. 0,00778 D. 0,03989
Câu 12. Một máy tự động có tỷ lệ phế phẩm là 2%. Trong 400 sản phẩm do máy sản
xuất ra thì số chính phẩm có khả năng nhiều nhất là A. 396 hoặc 397 B. 392 hoặc 393 C. 392 D. 397
Câu 13. Tung một con xúc xắc cho tới khi được mặt chẵn chấm thì dừng. Xác suất để
người đó phải tung số chẵn lần là A. 6/33 B. 1/3 C. 3/56 D. 5/11
Câu 14. Một người góp x (ngàn đồng) tham gia một trò chơi như sau: Gieo đồng thời
2 con xúc xắc cân đối đồng chất, nếu được 2 mặt 6 chấm thì được 100 000đ; 1 mặt 6
chấm thì được 26 000đ. Giá trị của x để về trung bình người chơi hòa vốn là A. 10 B. 15 C. 17 D. 20
Câu 15. Cho hai biến ngẫu nhiên độc lập X, Y và bằng A. 0,01 B. 0,025 C. 0,05 D. 0,1
Câu 16. Tung hai con xúc xắc đối xứng và đồng chất trên mặt phẳng. Gọi X là tổng số
chấm xuất hiện ở mặt trên của hai con xúc xắc đó. F(x) là hàm phân bố xác suất của
X; F(x) = + m khi 10 < x 11. Giá trị của m bằng A. 2/3 B. 1/2 C. 1/6 D. 3/4
Câu 17. Tiến hành bắn 3 phát súng vào bia, điểm tối đa của mỗi phát là 10. Biết xác
suất được 8 hoặc 9 điểm đều bằng 0,25, xác suất dưới 8 điểm bằng 0,4; còn xác suất
đạt 30 điểm với 3 lần bắn là 0,001. Xác suất để đạt tổng số 28 điểm là A. 0,05681 B. 0,02625 C. 0,06855 D. 0,07827
Câu 18.. Cho biến ngẫu nhiên rời rạc có bảng phân phối xác suất như sau X 0 1 2 3 4 P a 3a A 3a 2a
Giá trị k lớn nhất sao cho bằng A. 1 B. 2 C. 3 D. 4 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu
Hà Nội, ngày 01 tháng 06 năm 2022 GV giảng dạy
ThS. Phan Thị Hương KHOA CƠ BẢN
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ BỘ MÔN TOÁN TOA201.3(tháng 6/2022)
Thời gian: 50 phút (không được sử dụng tài liệu) Điểm
Họ và tên: ………………………………………………...
Lớp:…………………………… STT:…………………...
Chú ý: Thí sinh lựa chọn A, B, C, D điền vào ô trả lời tương ứng. Nếu có kết quả
khác các phương án trong đề, thí sinh ghi rõ kết quả đó thay vì ghi A, B, C, D.
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 TL
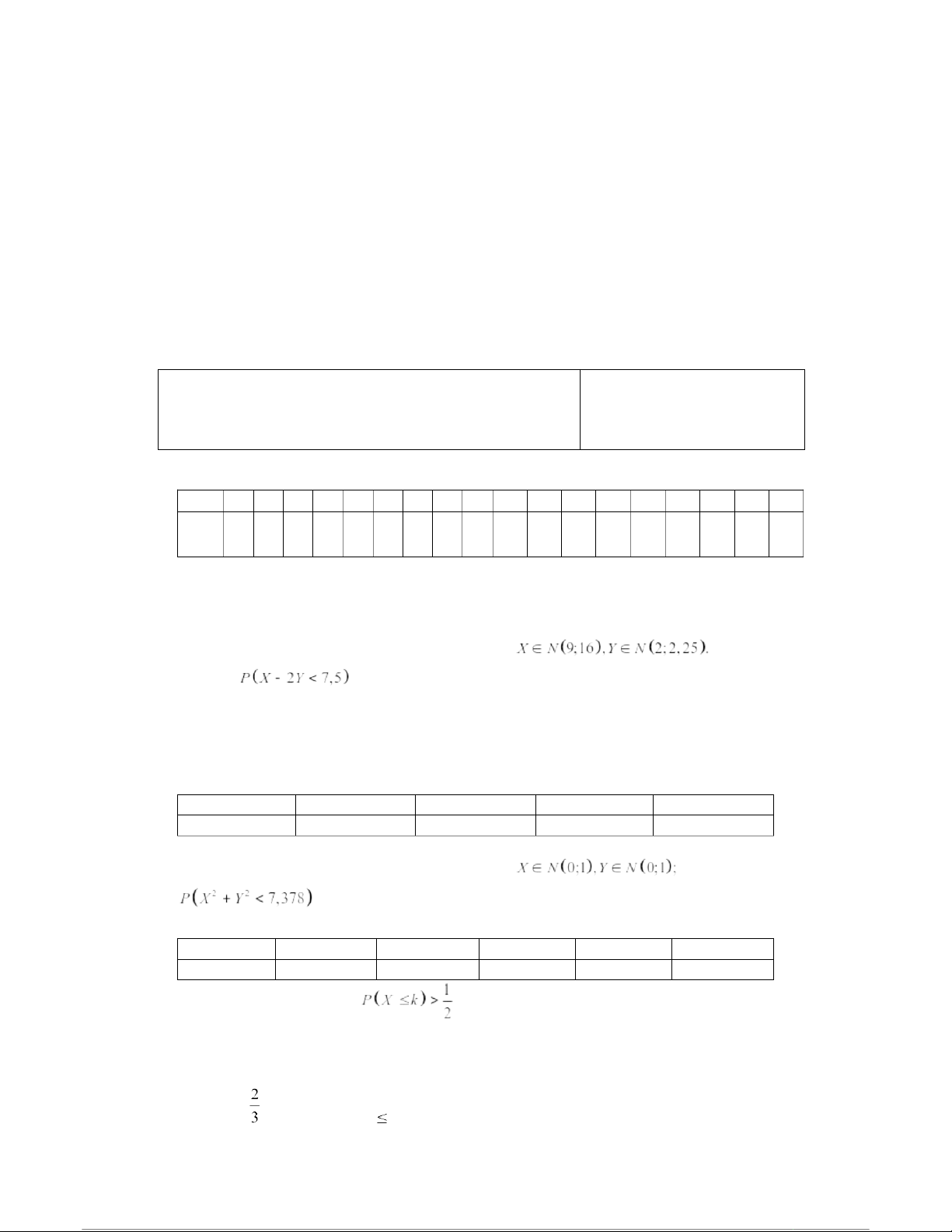
Câu 1. Một đoàn tàu gồm 3 toa đỗ ở sân ga. Có 4 hành khách mới bước lên tàu. Mỗi
hành khách độc lập với nhau chọn ngẫu nhiên một toa. Xác suất để mỗi toa có ít nhất
một hành khách mới bước lên là A. 1/16 B. 3/16 C. 7/16 D. 9/16
Câu 2. Cho hai biến ngẫu nhiên độc lập X, Y và Khi đó xác suất bằng A. 0,6368 B. 0,6517 C. 0,6736 D. 0,6915
Câu 3 .Tỷ lệ phế phẩm của một lô hàng là 1%. Cần phải lấy ít nhất bao nhiêu sản
phẩm từ lô hàng đó để với xác suất lớn hơn 0,95 được ít nhất 1 phế phẩm là A. 297 B. 298 C. 299 D. 296
Câu 4. Cho biến ngẫu nhiên rời rạc có bảng phân phối xác suất như sau X -5 -1 2 3 P 0,15 0,25 P 0,35 V(X) bằng A. 7,5962 B. 7,6184 C. 7,9253 D. 7,8475
Câu 5. Cho hai biến ngẫu nhiên độc lập X, Y và bằng A. 0,9 B. 0,925 C. 0,95 D. 0,975
Câu 6. Cho biến ngẫu nhiên rời rạc có bảng phân phối xác suất như sau X 0 1 2 3 4 P a 3a A 3a 2a
Giá trị k nhỏ nhất sao cho bằng A. 1 B. 2 C. 3 D. 4
Câu 7. Tung hai con xúc xắc đối xứng và đồng chất trên mặt phẳng. Gọi X là tổng số
chấm xuất hiện ở mặt trên của hai con xúc xắc đó. F(x) là hàm phân bố xác suất của
X; F(x) = + m khi 11 < x 12. Giá trị của m bằng 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu A. 23/36 B. 5/36 C. 17/36 D. 11/36
Câu 8. Cho A và B là các biến cố sao cho P(A) = 3/5; P(B) = 3/7; P(A + B) = 6/7. Khi đó bằng A. 3/7 B. 4/7 C. 2/7 D. 5/7
Câu 9. Thời gian đi từ nhà đến trường của một sinh viên A là một biến ngẫu nhiên X
(đơn vị là phút) có phân phối chuẩn N
. Biết rằng số ngày A đến trường mất ít
hơn 20 phút chiếm tỷ lệ 35,2% và số ngày A đến trường mất hơn 30 phút chiếm tỷ lệ
11,12%. Giá trị của và bằng A. 22,645; 5,58
B. 22,375; 6,25 C. 22,425; 6,45 D. 22,195; 6,65
Câu 10. Chọn khẳng định sai trong các khẳng định sau
A. P(A + B) = P(A) + P(B) suy ra A, B là hai biến cố xung khắc
B. Nếu biến cố A kéo theo biến cố B thì P(A) P(B) C.
thì với n không đổi, phương sai của nó lớn nhất khi p = 1/2 D. độc lập thì cũng độc lập
Câu 11. Trọng lượng của sản phẩm là biến ngẫu nhiên phân phối chuẩn có E(X) = 3
kg. Biết P(2 < X < 4) = 0,62. Sản phẩm được coi là đạt tiêu chuẩn nếu trọng lượng của
nó lớn hơn 2 kg. Tỷ lệ phế phẩm là A. 0,1556 B. 0,1806 C. 0,1900 D. 0,1950
Câu 12. Có 12 hộp bi, trong đó có 5 hộp loại I, mỗi hộp có 4 bi trắng và 5 bi đỏ; 3 hộp
loại II, mỗi hộp có 3 bi trắng, 9 bi đỏ; 4 hộp loại III, mỗi hộp có 8 bi trắng, 7 bi đỏ.
Lấy ngẫu nhiên ra một hộp, rồi từ hộp đó lấy ngẫu nhiên ra 2 bi. Xác suất để lấy được hai bi trắng là A. 0,4128 B. 0,3851 C. 0,2382 D. 0,1697
Câu 13. Với đầu bài câu 12, biết rằng hai bi lấy ra là hai bi trắng. Xác suất để hai bi
đó thuộc hộp loại III là A. 0,3732 B. 0,2153 C. 0,5238 D. 0,2308
Câu 14. Chiều cao của nam giới trưởng thành (tính bằng cm) ở một vùng dân cư là
biến ngẫu nhiên phân phối chuẩn N
. Xác suất để lấy ngẫu nhiên 3 thanh niên
thì có đúng 2 thanh niên có chiều cao từ 163 cm đến 171 cm là: A. 0,2407 B. 0,2509 C. 0,2608 D. 0,2706
Câu 15. Một máy tự động có tỷ lệ phế phẩm là 5%. Trong 400 sản phẩm do máy sản
xuất ra thì số phế phẩm có khả năng nhiều nhất là A. 20 hoặc 21 B. 10 hoặc 11 C. 20 D. 19
Câu 16. Tung một con xúc xắc cho tới khi được mặt chẵn chấm thì dừng. Xác suất để
người đó phải tung số lẻ lần là A. 6/11 B. 2/3 C. 6/33 D. 5/11
Câu 17.. Một người góp x (ngàn đồng) tham gia một trò chơi như sau: Gieo đồng thời
2 con xúc xắc cân đối đồng chất, nếu được 2 mặt cùng số chấm thì được thưởng 60
000đ; 2 mặt xuất hiện số chấm liên tiếp nhau thì được thưởng 36 000đ. Giá trị của x
để về trung bình người chơi hòa vốn là A. 10 B. 15 C. 17 D. 20
Câu 18. Cho 3 biến cố A, B, C. Biết P(A) = 0,23; P(B) = 0,18; P(C) = 0,34; P(AB) =
0,24; P(AC) = 0,15; P(BC) = 0,14; P(ABC) = 0,08. Xác suất để ít nhất 2 trong 3 biến
cố A, B, C xảy ra là A. 0,0800 B. 0,7000 C. 0,4000 D. 0,0203 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu
Hà Nội, ngày 01 tháng 06 năm 2022 GV giảng dạy
ThS. Phan Thị Hương 21:07, 10/01/2026
ĐỀ KIỂM TRA GIỮA KỲ MÔN XÁC SUẤT THỐNG KÊ TOA201.3 - ĐÁP ÁN 2023 - Studocu