Đề kiểm tra Hình học 11 chương 1 trường THPT Thừa Lưu – Thừa Thiên Huế

Đề kiểm tra Hình học 11 chương 1 trường THPT Thừa Lưu – Thừa Thiên Huế gồm 2 mã đề, mỗi mã đề gồm 3 bài toán tự luận, thời gian làm bài 45 phút, nội dung kiểm tra thuộc chủ đề 

40 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

3 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trường THPT Thừa Lưu
Tổ Toán
KIỂM TRA 1 TIẾT – CHƯƠNG I
HÌNH HỌC 11 CB
ĐỀ 1
Câu 1: (3,5 điểm)
Trong mặt phẳng Oxy, cho điểm
( 3;2)M
và đường thẳng
d
có phương trình
:4 3 1 0xy
.
Tìm ảnh của điểm
M
và đường thẳng
d
qua phép tịnh tiến theo véctơ
(1; 4)v 
Câu 2: (2,5 điểm)
Trong mặt phẳng Oxy, cho đường tròn
:
22
3 2 25xy
và điểm
(4; 5)A
Tìm ảnh của đường tròn
và điểm
A
qua phép quay
0
( ,90 )O
Q
Câu 3: (4 điểm)
a) Trong mặt phẳng Oxy, Cho đường tròn
:
2
2
( 1) 2 9xy
. Tìm đường tròn
()C
là ảnh của đường tròn
qua phép vị tự tâm O tỉ số
2k
b) Cho lục giác đều
ABCDEF
tâm O. Tìm ảnh của tam giác
AOF
bằng cách thực hiện
liên tiếp phép
0
( ,120 )O
Q
và phép
BO
T
Trường THPT Thừa Lưu
Tổ Toán
KIỂM TRA 1 TIẾT – CHƯƠNG I
HÌNH HỌC 11 CB
ĐỀ 2
Câu 1: (3,5 điểm)
Trong mặt phẳng Oxy , cho điểm A(3;2) , đường thăng d có phương trình : 3x+y-4=0
Tìm ảnh của điểm A và đường thẳng d qua phép tịnh tiến theo
(4; 3)v 
Câu 2: (2,5 điểm).
Trong mặt phẳng Oxy, cho đường tròn
: (x + 2)
2
+ (y – 3)
2
= 9 và điểm M(3 ;3)
Tìm ảnh của đường tròn
và điểm M qua
0
( ,90 )O
Q
.
Câu 3: (4điểm).
a/Trong mặt phẳng Oxy , cho đường tròn
: (x -5)
2
+ (y +2)
2
= 16 . Tìm ảnh của đường tròn
qua phép vị tự tâm O(0;0) tỉ số k=-3
b/ Cho hình vuông ABCD có M,N,P,Q lần lượt là trung điểm của AD,AB,BC,CD gọi O là
giao điểm của AC,BD,MP,NQ. Tìm ảnh tam giác MAO bằng cách thực hiện liên tiếp hai phép
dời hình là
0
( , 90 )O
Q
và phép tịnh tiến theo
MD
ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 11CB
ĐỀ1
Câu
Đáp án
Thang
điểm
1
•
( ) ;
v
M M x yT
MM v
3 1 2
2 4 2
x
y
2; 2M
• giả sử
;M x y d
.Khi đó
( ) ;
v
M M x yT
MM v
1
4
xx
yy


1
4
xx
yy


thay
vào phương trình của
d
ta được:
4 1 3 4 1 0xy

4 3 15 0xy

Vậy
()
v
ddT
:
4 3 15 0xy
1,5
1
1
2
•
0
,90
( ) ;
O
A A x yQ



0
, 90
OA OA
OA OA
5
4
xy
yx

5;4A
•Đường tròn (C) có tâm
3;2I
, bán kính
5R
Phép quay
0
,90
( ) ;
O
I I x yQ



2
3
xy
yx
2; 3I
Gọi
()C
là ảnh của
qua
0
( ,90 )O
Q
()C
có tâm
2; 3I

và bán kính
5RR

pt
()C
là:
2
2
( 2) 3 25xy
1
1,5
3a
• Đường tròn (C) có tâm
1;2I
, bán kính
3R
Phép vị tự
,2
( ) ;
O
I I x yV
2.1 2
2.2 4
x
y


2;4I
Gọi
()C
là ảnh của
qua
( ,2)O
V
()C
có tâm
2;4I
và bán kính
2.3 6R k R
pt
()C
là:
2
2
( 2) 4 36xy
0,5
0,75
0,75
3b
0
,120
()
O
AOF COBQ



()
BO
COB DEOT
0,5
0,75
0,75
ĐỀ2
câu
Nội dung
Điểm
Câu1
Gọi A’(x’ ;y’) là ảnh của A qua phép tịnh tiến theo vectơ
(4; 3)v 
Theo biểu thức tọa độ về phép tịnh tiến suy ra A’(7; -1)
Theo tính chất của phép tịnh tiến biến đường thẳng d thành đường
thẳng d’ suy ra d’ có dạng : 3x+y+m=0
A’(7 ;-1) là ảnh của A qua phép tịnh tiến theo vec tơ
(4; 3)v 
suy
ra A’ thuộc d’ nên: m=-20
Vậy d’ : 3x+y-20=0
1,5đ
2,0đ
Câu 2
Theo tính chất của phép
0
( ,90 )O
Q
biến điểm M(3;3) thành điểm M’(-
3;3)
( kèm hình vẽ)
Ta có :
: (x + 2)
2
+ (y – 3)
2
= 9 có tâm I(-2; 3) ,R=3
Theo tính chất của phép
0
( ,90 )O
Q
biến đường tròn
thành đường
tròn
’ có bán kính R’=R=3
Gọi I’(x’; y’) là tâm của đường tròn
’ nên theo
0
( ,90 )O
Q
biến I thành I’(-3; -2)
vậy
’ : (x + 3)
2
+ (y +2
2
= 9
1,5 đ
1,5 đ
Câu
3a
Ta có : đường tròn có tâm I(5 ;-2) ; Bán kính R=4
theo định nghĩa của phép vị tự suy ra I’(x’ ;y’) là ảnh của A qua
phép vị tự tâm O(0,0) tỉ số k=-3 là I’(-15;6)
Theo tính chất của phép vị tự ta có R’=3R=12
Vậy đường tròn
’: (x +15)
2
+ (y -6)
2
=144.
1 đ
Câu
3b
Ảnh của tam giác MAO qua
0
( , 90 )O
Q
là Tam giác NBO và phép tịnh
tiến theo
MD
thì tam giác NBO biến thành tam giác OPQ
Vậy ảnh tam giác MAO bằng cách thực hiện liên tiếp hai phép dời hình
là
0
( , 90 )O
Q
và phép tịnh tiến theo
MD
là tam giác OPQ
2 đ
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Trường THPT Thừa Lưu
KIỂM TRA 1 TIẾT – CHƯƠNG I Tổ Toán HÌNH HỌC 11 CB ĐỀ 1
Câu 1: (3,5 điểm)
Trong mặt phẳng Oxy, cho điểm M ( 3
 ;2) và đường thẳng d có phương trình
: 4x  3y 1  0 .
Tìm ảnh của điểm M và đường thẳng d qua phép tịnh tiến theo véctơ v  (1; 4  )
Câu 2: (2,5 điểm)
Trong mặt phẳng Oxy, cho đường tròn 2 2
(C) :  x  3   y  2  25 và điểm ( A 4; 5  )
Tìm ảnh của đường tròn (C) và điểm A qua phép quay Q 0 (O,90 )
Câu 3: (4 điểm)
a) Trong mặt phẳng Oxy, Cho đường tròn (C) : x    y  2 2 ( 1) 2  9 . Tìm đường tròn (C )
 là ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số k  2
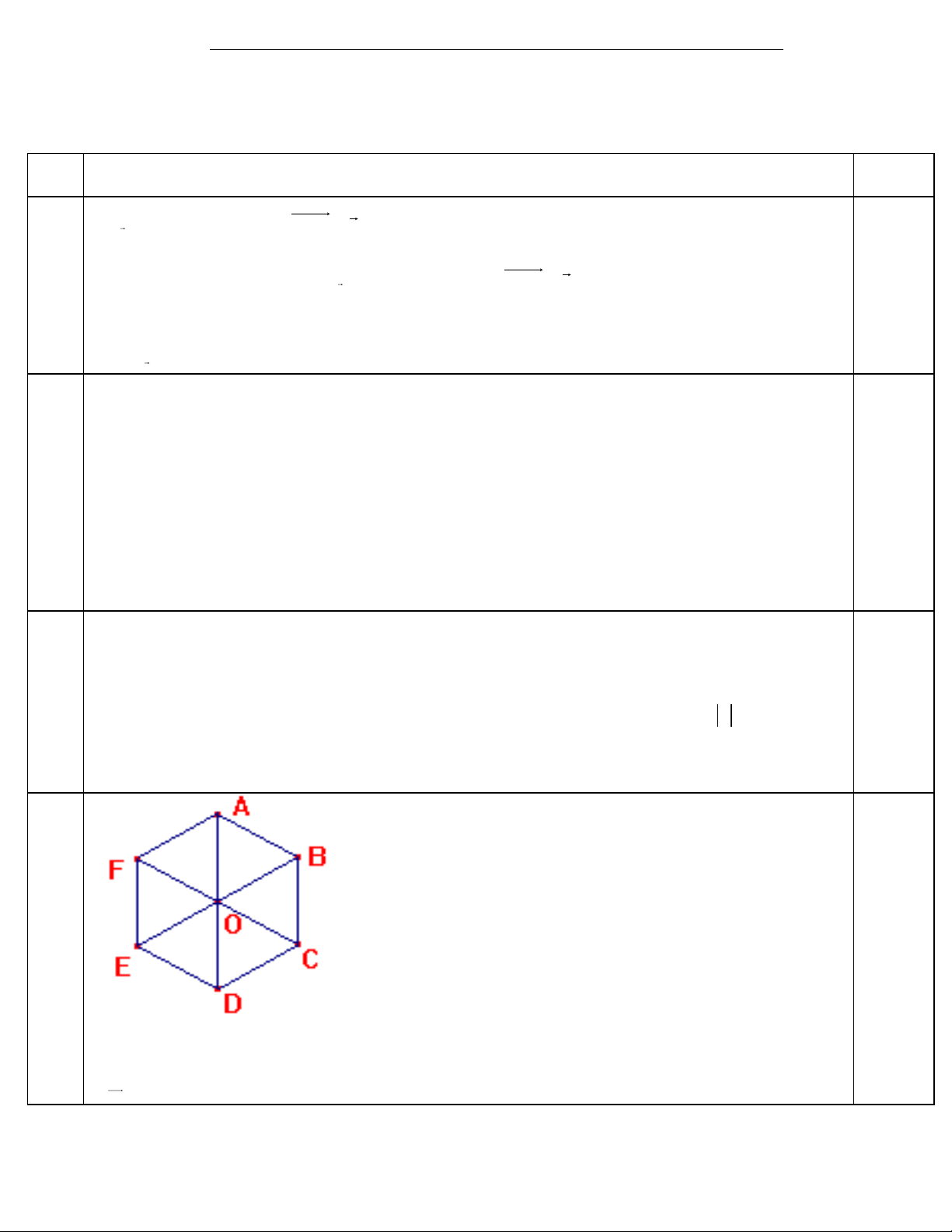
b) Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác AOF bằng cách thực hiện liên tiếp phép Q và phép T 0 (O,120 ) BO
Trường THPT Thừa Lưu
KIỂM TRA 1 TIẾT – CHƯƠNG I Tổ Toán HÌNH HỌC 11 CB ĐỀ 2 Câu 1: (3,5 điểm)
Trong mặt phẳng Oxy , cho điểm A(3;2) , đường thăng d có phương trì nh : 3x+y-4=0
Tìm ảnh của điểm A và đường thẳng d qua phép tịnh tiến theo v  (4; 3  ) Câu 2: (2,5 điểm).
Trong mặt phẳng Oxy, cho đường tròn (C) : (x + 2)2 + (y – 3)2 = 9 và điểm M(3 ;3)
Tìm ảnh của đường tròn (C) và điểm M qua Q . 0 (O,90 ) Câu 3: (4điểm).
a/Trong mặt phẳng Oxy , cho đường tròn (C) : (x -5)2 + (y +2)2 = 16 . Tìm ảnh của đường tròn
qua phép vị tự tâm O(0;0) tỉ số k=-3
b/ Cho hình vuông ABCD có M,N,P,Q lần lượt là trung điểm của AD,AB,BC,CD gọi O là
giao điểm của AC,BD,MP,NQ. Tìm ảnh tam giác MAO bằng cách thực hiện liên tiếp hai phép dời hình là Q
và phép tịnh tiến theo MD 0 (O, 9  0 )
ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 11CB ĐỀ1 Câu Đáp án Thang điểm        1,5      x
• T (M ) M x ; y MM v  3 1 2   M  2  ; 2   v  
y  2  4  2 1
x  x 1
x x  • giả sử M  ;
x y  d .Khi đó T (M )  M  x ; y  MM  v    1  thay v
y  y  4
y y  4 1
vào phương trình của d ta được: 4 x  
1  3 y  4 1  0 
4x  3y 15  0
Vậy T (d)  d : 4x  3y 15  0 1 v OA  OA
x   y  • Q ( ) A A     5   A5; 4   x ; y   1 0  , O 90   OA OA   0 ,  90
y  x  4   
•Đường tròn (C) có tâm I  3
 ;2 , bán kính R  5 2 
x   y  2 Phép quay Q (I )  I     I  2  ; 3    
x ; y    0  O,90 
y  x  3 1,5  
Gọi (C ) là ảnh của (C) qua Q  (C )  có tâm I 2  ; 3
  và bán kính R  R  5 0 (O,90 )  pt (C )  là: x    y  2 2 ( 2) 3  25
• Đường tròn (C) có tâm I 1;2 , bán kính R  3 0,5  x  2.1  2 3a Phép vị tự  V
I I xy    I 2; 4 O  ( )  ;  ,2 y  2.2  4 0,75 Gọi (C )
 là ảnh của (C) qua V  (C )
 có tâm I2;4 và bán kính R  k R  2.3  6 (O,2)
 pt (C ) là: x    y  2 2 ( 2) 4  36 0,75 3b 0,5 0,75 Q ( AOF)  COB  0 O,120      T ( COB)  DEO 0,75 BO ĐỀ2 câu Nội dung Điểm
Câu1 Gọi A’(x’ ;y’) là ảnh của A qua phép tịnh tiến theo vectơ v  (4; 3  )
Theo biểu thức tọa độ về phép tịnh tiến suy ra A’(7; -1) 1,5đ
Theo tính chất của phép tịnh tiến biến đường thẳng d thành đường
thẳng d’ suy ra d’ có dạng : 3x+y+m=0
A’(7 ;-1) là ảnh của A qua phép tịnh tiến theo vec tơ v  (4; 3  ) suy
ra A’ thuộc d’ nên: m=-20 2,0đ Vậy d’ : 3x+y-20=0
Câu 2 Theo tính chất của phép Q
biến điểm M(3;3) thành điểm M’(- 0 (O,90 ) 3;3) ( kèm hình vẽ) 1,5 đ
Ta có : (C): (x + 2)2 + (y – 3)2 = 9 có tâm I(-2; 3) ,R=3
Theo tính chất của phép Q
biến đường tròn (C) thành đường 0 (O,90 ) tròn
(C) ’ có bán kính R’=R=3
Gọi I’(x’; y’) là tâm của đường tròn
(C) ’ nên theo Q 0 (O,90 ) 1,5 đ biến I thành I’(-3; -2)
vậy (C)’ : (x + 3)2 + (y +22 = 9 Câu 3a
Ta có : đường tròn có tâm I(5 ;-2) ; Bán kính R=4 1 đ
theo định nghĩa của phép vị tự suy ra I’(x’ ;y’) là ảnh của A qua
phép vị tự tâm O(0,0) tỉ số k=-3 là I’(-15;6)
Theo tính chất của phép vị tự ta có R’=3R=12
Vậy đường tròn (C)’: (x +15)2 + (y -6)2 =144.
Câu Ảnh của tam giác MAO qua Q
là Tam giác NBO và phép tịnh 0 (O, 9  0 ) 3b
tiến theo MD thì tam giác NBO biến thành tam giác OPQ
Vậy ảnh tam giác MAO bằng cách thực hiện liên tiếp hai phép dời hình 2 đ là Q
và phép tịnh tiến theo MD là tam giác OPQ 0 (O, 9  0 )