Đề kiểm tra học kỳ 1 Toán 11 năm 2019 – 2020 trường Trưng Vương – TP HCM

TRƯỜNG THPT TRƯNG VƯƠNG KIỂM TRA HỌC KÌ I NĂM HỌC 2019 - 2020
Môn: Toán - Khối: 11 - Thời gian làm bài: 90 phút -----o0o-----
Họ, tên học sinh : ................................................ ..... Số báo danh :………………
Bài 1: (2,0 điểm) Giải các phương trình lượng giác : a) 2 3cos x  2sin x  0
b) sin 5x  3 cos 5x  1 .
Bài 2: (1,5 điểm) a) Giải phương trình : 3 2 A  C  70 n n b) Tính tổng : 1 3 5 2019 S  C  C  C  ... C . 2020 2020 2020 2020
Bài 3: (1,0 điểm) Cho tập hợp X = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 }. Từ tập X có thể lập được bao nhiêu số tự nhiên
gồm năm chữ số đôi một khác nhau sao cho luôn có mặt chữ số 1 ? 4  1 
Bài 4: (0,5 điểm) Tìm hệ số của số hạng chứa x6 trong khai triển của 6 2 (2x 1) x  x    .  4 
Bài 5: (1,0 điểm) Một hộp chứa 19 viên bi gồm 8 bi xanh, 6 bi trắng và 5 bi đỏ. Lấy ra ngẫu nhiên 4 viên bi từ
hộp trên. Gọi A là biến cố “Có đủ cả ba màu xanh, trắng và đỏ trong 4 bi được lấy ra”. Tính xác suất của biến cố A.
Bài 6: (4,0 điểm) Cho hình chóp S.ABCD với ABCD là hình thang có đáy lớn là đoạn AD, biết AD = 2BC, O
giao điểm của 2 đường chéo AC và BD. Gọi M là trung điểm của đoạn SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Tìm giao điểm I của đường thẳng BM với mặt phẳng (SAD) và chứng minh IC // SB.
c) Gọi K là trọng tâm của tam giác SCD. Chứng minh OK // (SBC).
d) Gọi () là mặt phẳng chứa OK và song song với AD. Tìm thiết diện của () với hình chóp S.ABCD. --- HẾT---
TRƯỜNG THPT TRƯNG VƯƠNG KIỂM TRA HỌC KÌ I NĂM HỌC 2019 - 2020
Môn: Toán - Khối: 11 - Thời gian làm bài: 90 phút -----o0o-----
Họ, tên học sinh : ................................................ ..... Số báo danh :………………
Bài 1: (2,0 điểm) Giải các phương trình lượng giác : a) 2 3cos x  2sin x  0
b) sin 5x  3 cos 5x  1 .
Bài 2: (1,5 điểm) a) Giải phương trình : 3 2 A  C  70 . n n b) Tính tổng : 1 3 5 2019 S  C  C  C  ...  C . 2020 2020 2020 2020
Bài 3: (1,0 điểm) Cho tập hợp X = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 }. Từ tập X có thể lập được bao nhiêu số tự nhiên
gồm năm chữ số đôi một khác nhau sao cho luôn có mặt chữ số 1 ? 4  1 
Bài 4: (0,5 điểm) Tìm hệ số của số hạng chứa x6 trong khai triển của 6 2 (2x 1) x  x    .  4 
Bài 5: (1,0 điểm) Một hộp chứa 19 viên bi gồm 8 bi xanh, 6 bi trắng và 5 bi đỏ. Lấy ra ngẫu nhiên 4 viên bi từ
hộp trên. Gọi A là biến cố “Có đủ cả ba màu xanh, trắng và đỏ trong 4 bi được lấy ra”. Tính xác suất của biến cố A.
Bài 6: (4,0 điểm) Cho hình chóp S.ABCD với ABCD là hình thang có đáy lớn là đoạn AD, biết AD = 2BC, O
giao điểm của 2 đường chéo AC và BD. Gọi M là trung điểm của đoạn SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Tìm giao điểm I của đường thẳng BM với mặt phẳng (SAD) và chứng minh IC // SB.
c) Gọi K là trọng tâm của tam giác SCD. Chứng minh OK // (SBC).
d) Gọi () là mặt phẳng chứa OK và song song với AD. Tìm thiết diện của () với hình chóp S.ABCD. --- HẾT--- TRƯỜNG THPT TRƯNG VƯƠNG KIỂM TRA HỌC KÌ I NĂM HỌC 2019 - 2020 Môn: Toán - Khối:11 -----o0o----- ĐÁP ÁN VÀ THANG ĐIỂM 1a a) 2 3cos x  2sin x  0 1b 1 3 1      sin 5x  cos 5x   sin 5x   sin 2  
 3cos x  2(1 cos x)  0 2 2 2  3  6 1đ 2
 2cos x  3cos x  2  0 1đ   2 x   k   cos x  2(L) 10 5 2   k Z    1  x    k2 7   2 cos x   3 x   k   2  30 5 2 . ĐK : n  N , n  3 3
Cách 1: Số cần lập n = abcde , a ≠ 0. a) 1đ 1đ n! n!    70 * TH1 : a = 1  bcde có 4 A = 360 cách chọn 6 (n  3)! 2!(n  2)! * TH2 : a ≠ 1  có 5. 3 C .4! = 1200 5 3 2
 2n  5n  3n 140  0  n  5
Vậy có 360 + 1200 = 1560 (số) b) 2n 0 1 2 2 3 3 2n 1  2n 1  2n 2
(1 x)  C  C x  C x  C x  ... n  C x  C x 2n 2n 2n 2n 2n 2n
Cách 2: Số cần lập n = abcde , a ≠ 0. 0.5 Cho x = 1 , x = –1
* Số n có cả chữ số 1 : 4 6.A = 2160 6 đ 0 1 2 3 2n 1  2n 2
C  C  C  C  ...  C  C  2 n (1) 2n 2n 2n 2n 2n 2n
* Số n không có chữ số 1 : 4 5.A = 600 5 0 1 2 3 2n 1  2 C  C  C  C  ... n  C  C  0 (2) 2n 2n 2n 2n 2n 2n  có 4 4 6.A  5.A = 1560 (số) 6 5
(1) – (2)  S = 22020 – 1 (n = 1010) 4 4 14  1   1  5 6 2 6 (2x 1) x  x   2  x     4 n()  C  3876 0.5  4   2  1đ 19 đ 14 1 1 2 1 2 1 2 1 1 n( )
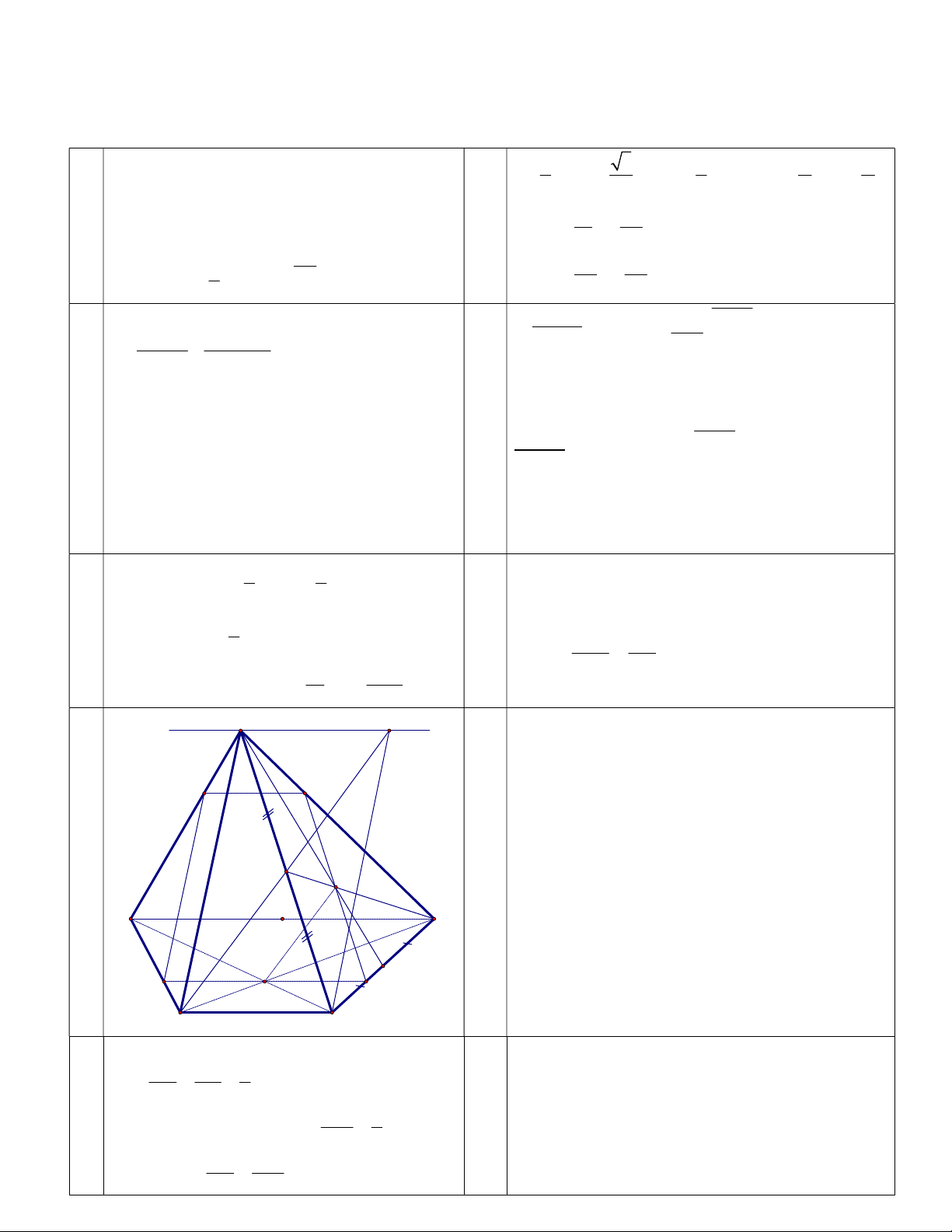
A  C C C  C C C  C C C  1920 8 5 6 8 5 6 8 5 6 k  1 k  SHTQ : 6 2 . ( )k C x 14    2  n( ) A 160 P( ) A   1 3003 n() 323 YCBT  k = 6. Hệ số : 6 C  2 14 2 4 6 S x S  (SAD)  (SBC) a) I  1đ AD  (SAD)   BC  (SBC) H Q P  Ì AD / /BC  N
 (SAD)  (SBC)  Sx / / A D / /B C H 0.5 M b) * Trong (SBC) : BM  Sx = I đ K I  BM  1đ   I  BM  (SAD) I  Sx  (SAD) A D 
*  MBC =  MIS  SI = BC E mà SI // BC O F
 SBCI là hình bình hành  IC // SB B C
*  OBC đồng dạng  ODA
+ ()  (ABCD) = EF qua O và EF // AD c) OB BC 1 d) + Trong (SCD): FK  SD = P    (1) OD DA 2
0.5đ  ()  (SCD) = FP 1đ KM 1 + ()  (SAD) = PQ // AD
* K là trọng tâm  SCD   (2) KD 2 + ()  (SAB) = EQ OB KM
Thiết diện là hình thang EFPQ ( EF // PQ ) (1) và (2)    OK // BM OD KD
mà BM  (SBC) , OK  (SBC)  OK // (SBC)