1
GV toán: Nguyễn Thế Bình
10 ĐỀ KIỂM TRA HỌC KỲ 1 2022 - 2023 ĐỀ SỐ 1
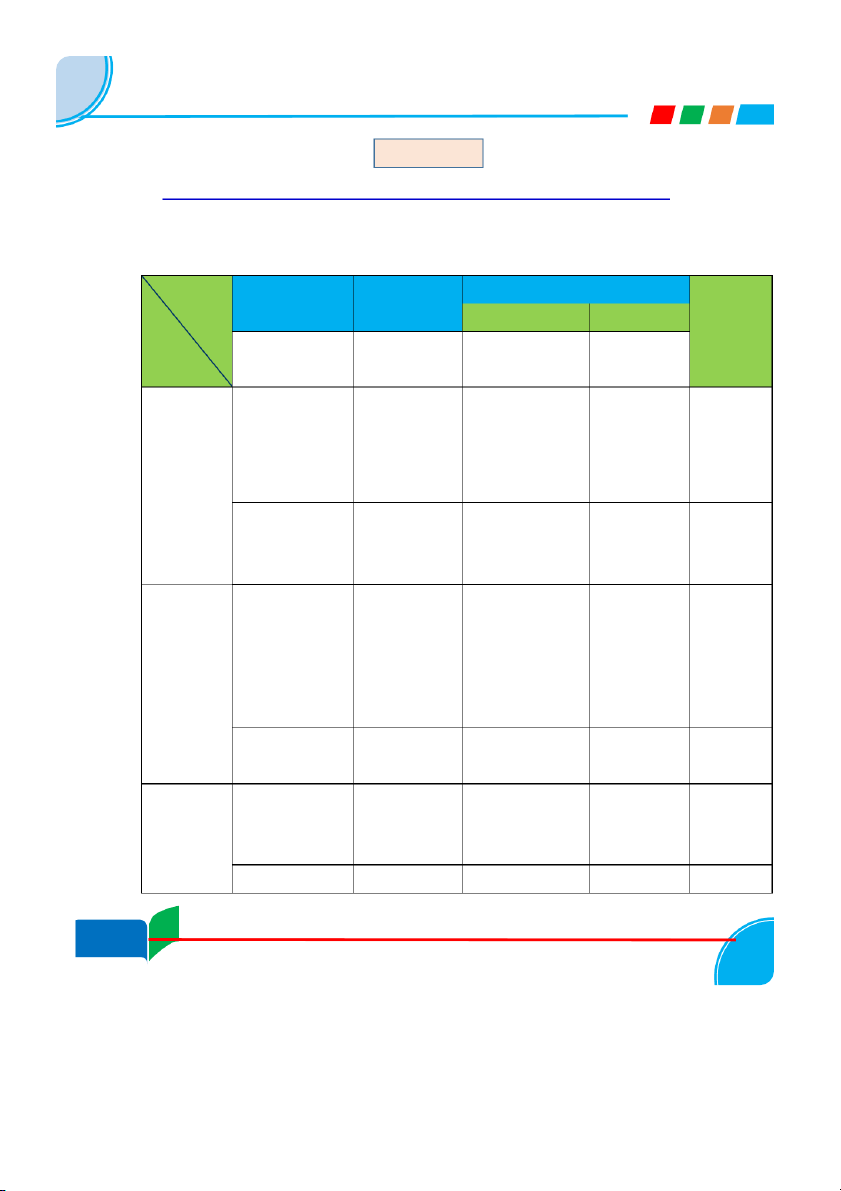
MA TRẬN ĐỀ KIỂM TRA Chủ đề
Nhận biết Thông hiểu V n ậ dụng Tổng
Vận dụng thấp
Vận dụng cao TN TL TN TL TN TL TN TL 1. Căn bậc
Biết được đk để Hiểu được căn bậc Sử dụngphép bđ đưa Giải phương trình hai căn thức có hai s h ố ọc thừa số ra ngoài dấu chứa căn bậc hai nghĩa, căn bậc căn. Sử dụng các hai c a ủ s ố phép biến đổi để thu không âm gọn biểu thức chứa căn bậc hai Số câu 1 1 2 1 5 Số m điể 0,25 0,25 1,5 1 3 Tỉ lệ 2,5% 2,5% 15% 10% 30% 2. Hàm số
Nhận biết được Xác định được Tìm đk để đường hàm s ố đồng
điểm thuộc đồ thị thẳng cắt nhau, song biến, hàm số hàm s ố song. Vẽ được đồ thị bậc nhất hàm s b ố ậc nhất Số câu 2 1 1 2 6 Số m điể 0,5 0,25 0,25 1,5 2,5 Tỉ lệ 5% 2,5% 2,5% 15% 25% 3. M t ộ s h ố ệ
Nhận biết được Hiểu được hệ thức
thức về cạnh tỉ s
ố lượng giác để tính độ dài
và đường cao. của góc nhọn đường cao Tỉ s ố lượng giác Số câu 1 1 2 Số m điể 0,25 0,25 0,5 Tỉ lệ 2,5% 2,5% 5%
4. Đường tròn Biết được số Hiểu được tính Chứng minh được 3
điểm chung của chất của đườ ố
ng n i điểm thẳng hàng và
đường thẳng và tâm. Tâm đường một đường thẳng là đường tròn.
tròn ngoại tiếp tam tiếp tuyến của đường Liên hệ giữa giác tròn 1/64 2
GV toán: Nguyễn Thế Bình đường kính và dây Số câu 2 2 2 6 Số m điể 0,5 0,5 3 4 Tỉ lệ 5% 5% 30% 40% Tổng s c ố âu 6 5 1 6 1 19 Tổng s ố điểm 1,5 1,25 0,25 6 1 10 Tỉ lệ 15% 12,5% 2,5% 60% 10% 100% ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM : (3 điểm )
Khoanh tròn vào chữ cái ở đầu câu với những câu trả lời đúng (mỗi câu đúng 0,25 điểm)
Câu 1. Với những giá trị nào của x thì x  2022 có nghĩa A. x > 2022 B. x > -2022 C. x ≥ 2022 D. x ≤ 2022
Câu 2. Căn bậc hai số học của 9 là: A. 81 B . 3 C.  81 D .  3
Câu 3. Đồ thị hàm số y = 2x -3 đ i qua điểm nào? A. (1; -3) B. (1; -5) C. (-1; -5) D. (-1; -1)
Câu 4. Hàm số y= (m - 5
)x + 2 là hàm số đồng biến khi nào? A. m <5 B. m >5 C. m <-5 D. m >-5
Câu 5. Để hàm số y = (m +1)x -3 là hàm số bậc nhất thì: A. m  1  B. m 1 C. m  1  D. m 1
Câu 6. Cho hàm số bậc nhất y = (m – 3)x – 4 và y = 4x. Giá trị của m để đồ thị của hai hàm số cắt nhau là: A. m  3 B. m  7 C. m  3  ,m  7 
D. m  3,m  7
Câu 7. Tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, AC = 8cm. Độ dài AH là: A. 3,5cm B. 4,6cm C. 4,8cm D. 5cm
Câu 8. Cho tam giác ABC vuông tại B. Khi đó SinC bằng: A. AB B. AC C. BC D. AB AC AB AC BC
Câu 9. Đường thẳng và đường tròn tiếp cắt nhau thì số điểm chung là: A. 0 B. 1 C. 2 D. 3
Câu 10. Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường nào? A. Phân giác B. Trung tuyến C. Đường cao D. Trung trực 2/64 3
Câu 11. Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm ở vị trí nào?
A. Nằm ngoài đường tròn
B. Nằm trên đường nối tâm
C.Nằm ngoài đường nối tâm D. Nằm trong đường tròn
Câu 12. Nếu AB là một dây bất kì của đường tròn (O; R) thì: A. AB  2R B. AB  2R C. AB  2R D. AB  R
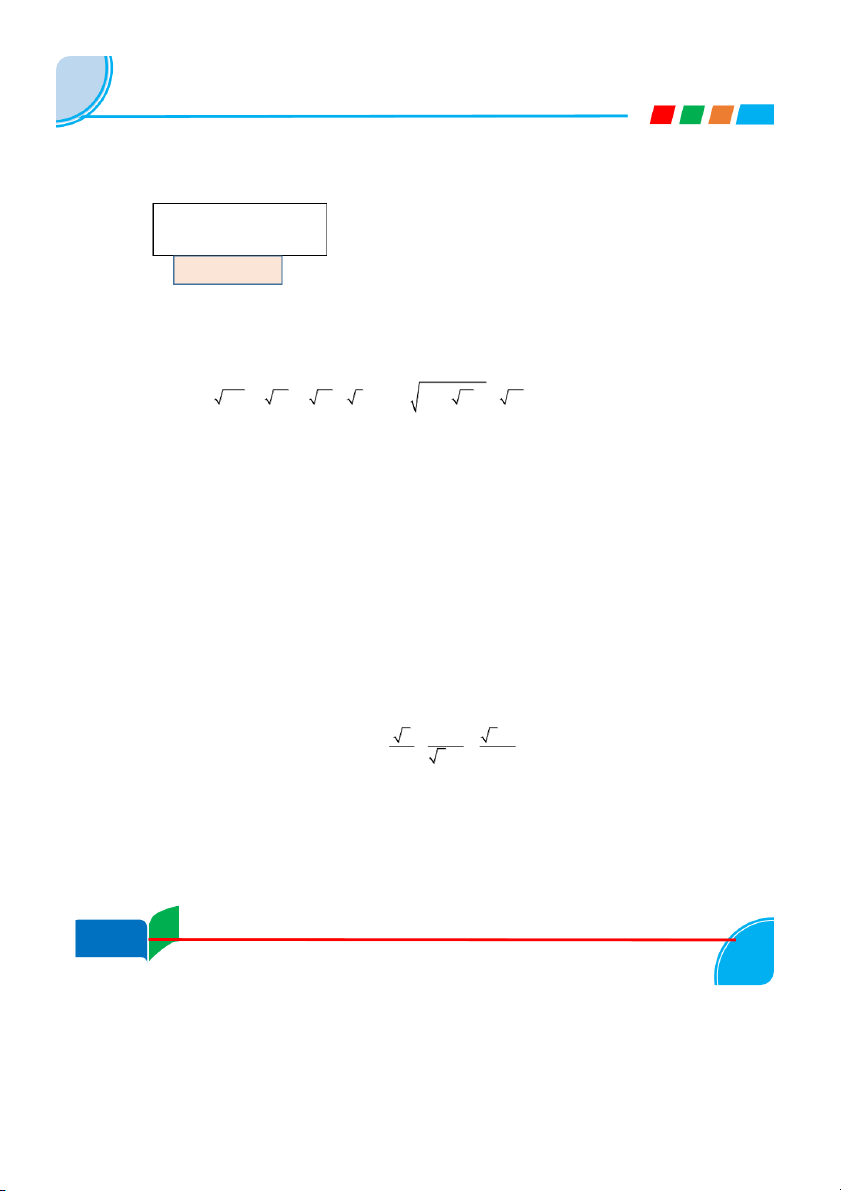
II/ PHẦN TỰ LUẬN : (7 điểm ) Bài 1. ( 1,5 điểm).
a) Tính M =  18  32  2019 2  x x  b) Rút gọn biểu thức 2 N     : (với x >0 và x  1)  x 1 x 1 x 1     
Bài 2. (1,5 điểm) Cho hàm số y = (m - 1)x +m +4 (1)
a) Vẽ đồ thị hàm số trên với m = -1.
b) Tìm m để đồ thị hàm số (1) song song với đồ thị hàm số y = -x + 2.
Bài 3. (3 điểm) Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn
tâm A, bán kính AH, kẻ các tiếp tuyến BD, CE với đường tròn tâm A (D, E là các
tiếp điểm khác H). Chứng minh rẳng:
a) Ba điểm D, A, E thẳng hàng;
b) DE tiếp xúc với đường tròn có đường kính BC.
Bài 4. (1 điểm) Giải phương trình: 2
x  2  3 x  4  0
.........HẾT........ 3/64 4
GV toán: Nguyễn Thế Bình
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
I.TRẮC NGHIỆM: ( 3 điểm ) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C B C B A D C A C D B A
Mỗi câu trả lời đúng 0,25đ
II.TỰ LUẬN ( 7 điểm ) Bài Nội dung – Đáp án Điểm 1.
a)M   18  32  2019 2 0,5đ  3 2  4 2  2019 2  2020 2  x x  2 0,5đ b) N     :  1 1  x x x 1      x. x  
1  x. x  1 2     : .  x x x    1 1 1 2 x 2 2 x x 1  :    x 0,5đ x 1 x 1 x 1 2 2.
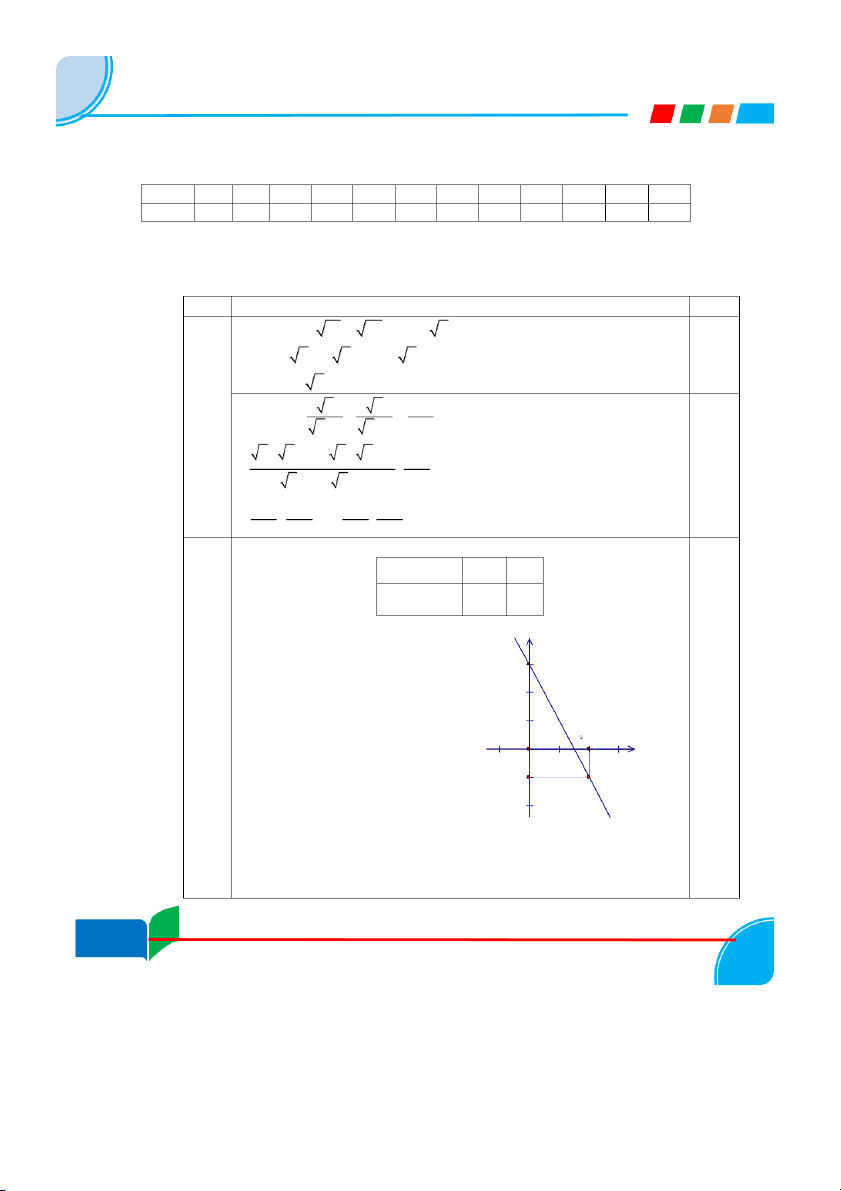
a) Khi m = -1, ta có hàm số y = -2x + 3 0,5đ x 0 1,5 y = -2x + 3 3 0
- Đồ thị hàm số y = -2x + 3 là đường thẳng đi qua hai điểm (0;3) và (1,5;0) - Vẽ đồ thị : y(d 3 ):y 2 = -2x+ O 2 0,5đ x - 1 -2
b) đồ thị hàm số y = (m - 1)x +m +4 (1) song song với đồ thị hàm m 1 1 m0 số y =       -x + 2      m  0 m  4  2 m     2 4/64 5
Vậy với m=0 thì đồ thị hàm số y = (m - 1)x +m +4 song song với
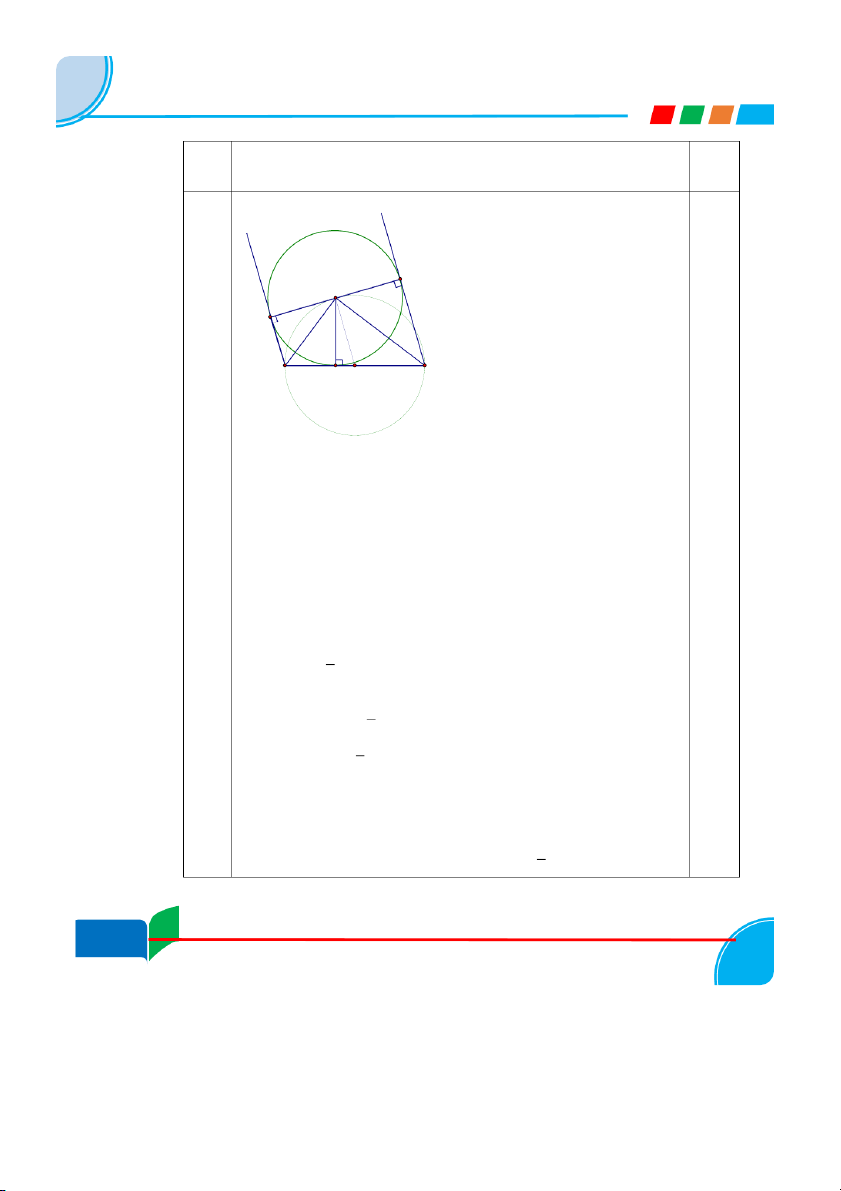
đồ thị hàm số y = -x + 2 0,5đ 3. E A 4 1 3 2 D B C H O Vẽ đúng hình 0,5đ
a) Ta có: BD và BH là hai tiếp tuyến của (A,AH) cắt nhau tại B Â1 = Â2
CE và CH là hai tiếp tuyến của (A,AH) cắt nhau tại C Â3 = Â4. Â 0
1 + Â2 + Â3 + Â4 = 2.(Â2 + Â3) = 180 . D, A, E thẳng hàng. 1đ
b) Gọi O là trung điểm của BC
OA = 1 BC ( t/c trung tuyến ứng cạnh huyền trong tam giác 2 vuông) A thuộc (O, 1 BC) 2
DE và (O, 1 BC) có điểm chung A. (1) 2
OA là đường TB của hình thang BCED
OA // BD // CE mà BD vuông góc với DE OA vuông góc với DE (2)
Từ (1) và (2) suy ra DE là tiếp tuyến của (O, 1 BC). 2 1,5đ 5/64 6
GV toán: Nguyễn Thế Bình 4 x 2  0 ĐK:   x  2 (1) 2 x  4  0  2
x  2  3 x  4  0
 x  2  3 (x  2)(x  2)  0
 x  2.1 3 x  2  0   x  2 x  2  0        1  3 x  2  17 (2)  0  x    9
Kết hợp (1) và (2) ta được: x = 2 Vậy x = 2 1đ
Chú ý : HS làm theo cách khách nếu đúng vẫn cho điểm tuyệt đối. 6/64 7 GV toán: Nguyễn Thế Bình ĐỀ SỐ 2
MA TRẬN ĐỀ KHẢO SÁT HỌC KỲ I- MÔN TOÁN 9.
Thời gian: 90 phút
NĂM HỌC: 2022 - 2023
Vận dụng Cấp độ
Nhận biết Thông hiểu
Cấp độ thấp
Cấp độ cao Cộng Chủ đề TL TL TL TL - Xác định điều -Hi c ểu đượ
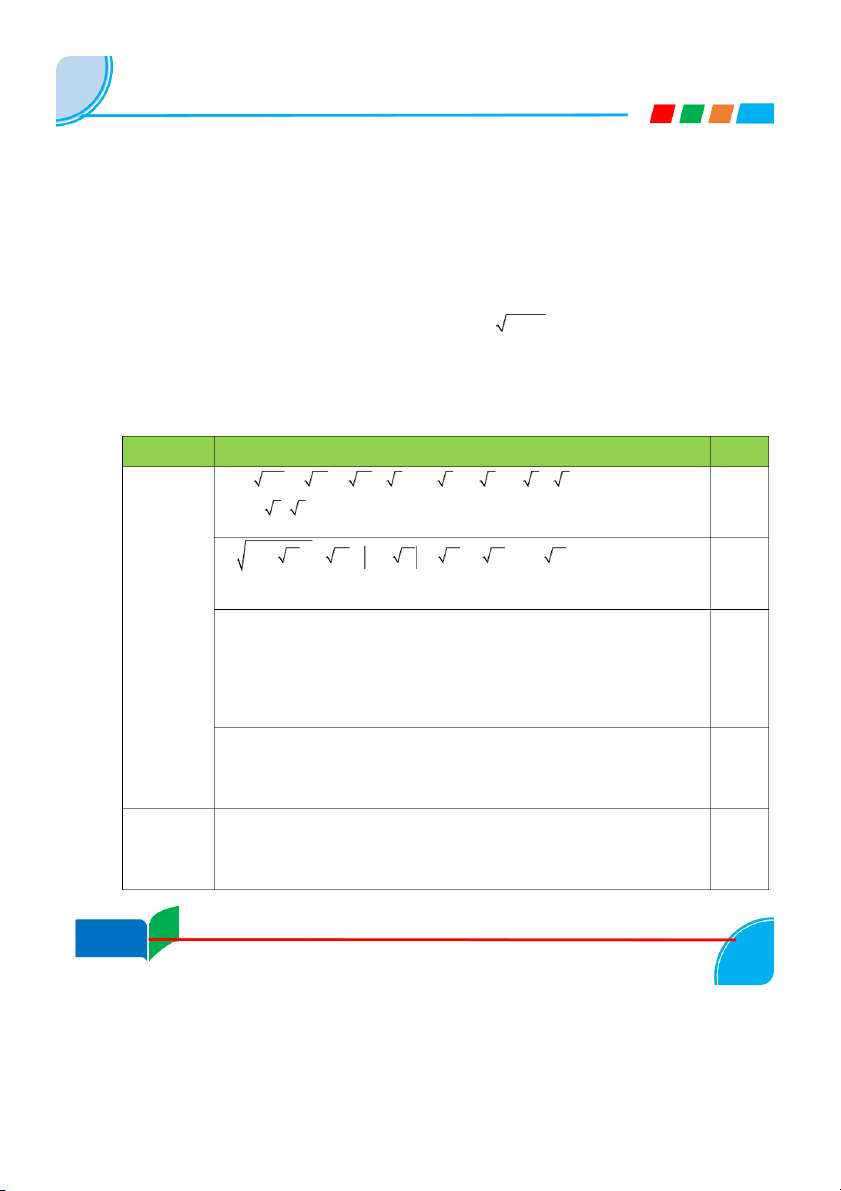
Vận dụng các phép Vận dụng các kiện có nghĩa của hằng đẳng thức biến đổi đơn giản phép biến đổi căn bậc hai. để rút gọn biểu để rút gọn biểu để rút gọn biểu thức thức, tính giá trị thức phức tạp, 1.Căn thức biểu thức giải phương trình vô tỷ bậc hai Số câu:2 Số câu:2 Số câu:2 Số câu:1
Số câu: 7 Số m điể :1 Số m điể :1 Số m điể : 1.
Số điểm:0,5
Số điểm:3.5 Nhận biết được Hiểu được hai Tìm được giao hàm s
ố đồng biến, đường thẳng điểm đồ thị của hai nghich biến song song,.. hàm s b ố ậc nhất Vẽ được đồ thị hàm s ố 2.Hàm số bậc nh t ấ Số câu:2 Số câu:2 Số câu:2
Số câu: 6
Số điểm:1
Số điểm:1
Số điểm:1
Số m điể : 3 Hiểu được các Vận dụng các hệ
3.Hệ thức
hệ thức áp dụng thức lượng trong lượng trong vào tam giác tam giác vuông để tam giác vuông giải toán vuông. Số câu:1 Số câu:1
Số câu: 2 7/64 9
GV toán: Nguyễn Thế Bình PHÒNG GD&ĐT ……….
ĐỀ KIỂM TRA CUỐI HỌC KỲ I
TRƯỜNG THCS ……..
NĂM HỌC: 2022 – 2023
ĐỀ CHÍNH THỨC
MÔN TOÁN – LỚP 9 (Đề gồm 01 trang)
Thời gian làm bài 90 phút (không kể thời gian phát ĐỀ SỐ 2 đề) Câu 1( 2 điểm):
1) Tính giá trị của biểu thức
a) 2 300 3 48 4 75 : 3 b)   2 3 2 15  60 2x  y  5
2) Giải hệ phương trình x y 1
3) Tìm a để phương trình ax + 3y =4 nhận cặp số (2;1) làm nghiệm
Câu 2 (2 điểm): Cho hàm số : y = (m – 1)x + 2m – 3 (1) với m là tham số
a/ Với giá trị nào của m thì hàm số (1) đồng biến
b/Vẽ đồ thị của hàm số trên khi m=2
c/ Tìm m để đồ thị hàm số (1) cắt đường thẳng y = 2x + 1 tại một điểm nằm trên trục tung.  
Câu 3 (2 điểm): Cho biểu thức A = x 1 x 1    :  x 1   x 1 x 1   
a) Tìm ĐKXĐ và rút gọn biểu thức A
b) Tìm giá trị của x để A< 0
c) Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên
Câu 4 (3.5 điểm): Cho đường tròn tâm O bán kính R và một điểm M nằm ngoài
đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm 9/64 10
GV toán: Nguyễn Thế Bình
giữa MA và MO cắt đường tròn (O; R) tại hai điểm C và D (C nằm giữa M và D).
Gọi I là trung điểm của dây CD, kẻ AH vuông góc với MO tại H. a/ Tính OH. OM theo R.
b/ Chứng minh: Bốn điểm M, A, I , O cùng thuộc một đường tròn.
c/ Gọi K là giao điểm của OI với HA. Chứng minh KC là tiếp tuyến của đường tròn (O)
Câu 5 (0.5điểm): Giải phương trình: 2 x  6x  26  6 2x 1
------------------------Hết------------------------ ĐÁP ÁN: Câu Nội dung đáp án Điểm
2 300 3 48 4 75: 3 20 3 1  2 3 20 3 : 3 0.5đ a) 12 3 : 3 12 1 0.5đ (2 điểm) b)   2
3 2 15  60  3  2 15  2 15  2 15  3 2 15  3  2x  y  5 3x  6 x  2 0.5đ 2)   x  y 1 x  y 1 y  1 x  2
Vậy hệ có nghiệm y 1
3)Vì phương trình ax + 3y =4 nhận cặp số (2;1) làm nghiệm nên: 0.5đ a.2+3.1=4=> a=1/2 2
y = (m – 1)x + 2m – 3 (1) với m là tham số 0.75đ
a/ Với giá trị nào của m thì hàm số (1) đồng biến 10/64 11
GV toán: Nguyễn Thế Bình (2 điểm)
Hàm số (1) đồng biến khi
a > 0 m – 1 > 0 m > 1
Vậy với m > 1 thì hàm số (1) đồng biến
b)Khi m=2 ta có hàm số y=x+1 HS vẽ đồ thị 0,75 đ
c/ Tìm m để đồ thị hàm số (1) cắt đường thẳng y = 2x + 1 tại một điểm 0,5 đ nằm trên trục tung.
- Vì đường thẳng y = 2x + 1 cắt trục tung tại điểm có tung độ bằng 1.
Đề đường thẳng (1) cắt đường thẳng y = 2x + 1 tại một điểm nằm trên m1 2 m  3 m  3       m  2
trục tung thì : 2m 3 1 2m  4 m     2
Vậy với m = 2 thì đồ thị hàm số (1) cắt đường thẳng y = 2x + 1 tại một
điểm nằm trên trục tung 3 a) Đk   (2điểm) A = x 1 x 1    :  ĐKXĐ: x 0; x 1 0.5đ x 1   x 1 x  1       = x x 1 x  1   :  ( 
x 1)( x  1)
( x 1)( x 1)     = 1  .   x 1 0.5đ ( x 1)( x   1)  = 1 x 1 b)Với x 1 0.5đ
 0; x 1để A<0  <0  x 1 0 x 1 11/64