Đề kiểm tra năng lực giáo viên môn Toán năm 2018 – 2019 sở GD và ĐT Bắc Giang

Đề kiểm tra năng lực giáo viên môn Toán năm 2018 – 2019 sở GD và ĐT Bắc Giang gồm 80 câu hỏi và bài toán trắc nghiệm khách quan, thời gian làm bài 90 phút, đề nhằm thúc đẩy quý thầy, cô giáo đang giảng dạy môn Toán phải luôn rèn luyện để nâng cao năng lực môn Toán

45 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

45 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 1 Mã đề 388
Tuonganh0209@gmail.com
Câu 1: Trong mặt phẳng với hệ trục
Oxy
, cho hai đường tròn
( ) ( )
2
2
: 1 4C x y− + =
và
( ) ( ) ( )
22
: 4 3 16C x y
− + − =
cắt nhau tại hai điểm phân biệt
A
và
B
. Lập phương trình đường
thẳng
AB
A.
20xy+ − =
. B.
2. 0xy− + =
C.
. D.
.
Câu 2: Một hình trụ có diện tích xung quanh bằng
16
và thiết diện qua trục của hình trụ này là một
hình vuông. Thể tích
V
A.
32 2
. B.
18
. C.
16
. D.
24
.
Câu 3: Một cấp số cộng gồm
5
số hạng. Hiệu số hạng đầu và số hạng cuối bằng
20
. Tìm công sai
d
của cấp số cộng đã cho
A.
5d =−
. B.
4d =
. C.
4d =−
. D.
5d =
.
Câu 4: Với hai véc tơ không cùng phương
a
và
b
. Xét hai véc tơ
23u a b=−
và
( 1)v a x b= + −
. Tìm
x để
u
và
v
cùng phương.
A.
3
2
x =
. B.
1
2
x =
. C.
1
2
x =−
. D.
3
2
x =−
.
Câu 5: Gi tr lớn nhất của hm số
2sin 1yx=+
l
A.
1−
. B.
1
. C.
1
2
−
. D.
3
.
Câu 6: Cho t diện ABCD. Gi
M
,
N
lần lưt l trung điểm của
BC
,
AD
. Biết
2AB a=
,
22CD a=
v
5.MN a=
Số đo gc gia hai đường thẳng
AB
v
CD
l
A.
60
. B.
30
. C.
90
. D.
45
.
Câu 7: Điều kiện xc đnh của phương trình
28xx− = −
là
A.
2;8x
. B.
8x
. C.
2x
. D.
8x
.
Câu 8: Mẹ hơn Minh
25
tuổi. Biết rằng
4
năm về trước tuổi của mẹ gấp
6
lần tuổi của Minh. Hãy
tính tuổi của Minh hiện nay.
A. 9 tuổi. B. 5 tuổi. C. 8 tuổi. D. 10 tuổi.
SỞ GD&ĐT BẮC GIANG
HỘI ĐỒNG KTKT GIÁO VIÊN
NĂM HỌC 2018 - 2019
------------------
ĐỀ THI TRẮC NGHIỆM
MÔN TOÁN THPT
Thời gian làm bài: 90 phút (80 câu trắc nghiệm)
MÃ ĐỀ: 385
(Giáo viên không được sử dụng tài liệu)
Họ tên giáo viên: ............................................................................... Ngày sinh: ................. SBD: .................
Trường: ......................................................................................... .... Huyện / thành phố: ...............................
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 2 Mã đề 388
Câu 9: Gi
1
x
,
2
x
là hai nghiệm của phương trình
2
22
log 3log 2 0xx− + =
. Tính
12
P x x=+
.
A.
6
. B.
3−
. C.
2
. D.
3
.
Câu 10: Cho hàm số
32
3 2 1y x x x= − − −
c đồ th
( )
C
. Phương trình tiếp tuyến với
( )
C
tại giao điểm
của
( )
C
với trục tung là
A.
21yx= − −
. B.
21yx=−
. C.
21yx=+
. D.
21yx= − +
.
Câu 11: Trong mặt phẳng với hệ trục ta độ
( )
;,O i j
, cho hai vectơ
2a i j=−
và
( )
4;2b =−
.
Khẳng
đnh no sau đây l đúng?
A.
a
và
b
cùng hướng
.
B.
a
và
b
ngưc hướng.
C.
( )
1;2a =−
. D.
( )
2;1a =
.
Câu 12: Cho hình chóp
.S ABCD
c đy
ABCD
là hình ch nhật,
( )
, 2 ,AB a AD a SA ABCD= = ⊥
và
SA a=
. Gi
M
l trung điểm của cạnh
SC
.
Khoảng cách từ
M
đến mặt phẳng
( )
SBD
bằng:
A.
.
2
a
B.
.
3
a
C.
4
.
3
a
D.
2
.
3
a
Câu 13: Biết
(
)
2
lim 4 1 1
x
x ax bx
→−
+ + + = −
. Tính giá của biểu thc
23
2P a b=−
.
A.
32P =
. B.
0P =
. C.
16P =
. D.
8P =
.
Câu 14: Xếp
6
hc sinh gồm
3
hc sinh nam và
3
hc sinh ngồi vào hai dãy ghế đối diện nhau, mỗi
dãy có
3
ghế (mỗi hc sinh ngồi một ghế, các ghế đều khác nhau). Hỏi có bao nhiêu cách xếp
sao cho không có hai hc sinh cùng giới ngồi đối diện nhau.
A. 720. B. 36. C. 288. D. 72.
Câu 15: Cho hình chóp
.S ABCD
c đy l hình vuông cạnh
a
,
SAB
l tam gic đều và nằm trong mặt
phẳng vuông góc với đy. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp
.S ABCD
A.
2
3Sa
=
. B.
2
4
3
a
S
=
. C.
2
7
3
a
S
=
. D.
2
7Sa
=
.
Câu 16: Tìm x để hai vectơ
( ;2)ax=
và
(2; 3)b =−
có giá vuông góc với nhau.
A. 3. B. 0. C.
3−
. D. 2.
Câu 17: Trong mặt phẳng với hệ ta độ Oxy, cho elip
( )
22
:1
25 9
xy
E +=
. Tiêu cự của (E) bằng
A. 10. B. 16. C. 4. D. 8.
Câu 18: Cho hai tập hp
)
1;3A =−
và
1;5B =
. Giao của A và B là tập hp no sau đây?
A.
1;5−
. B.
)
1;3
. C.
1;3
. D.
1;2
.
Câu 19: Biết các nghiệm của phương trình
có dạng
xk
m
=+
và
xk
n
= − +
,
k
;
với
,mn
là các số nguyên dương. Khi đ
mn+
bằng
A. 4. B. 3. C. 5. D. 6.
Câu 20: Cho số phc
12zi=−
. Tìm số phc
2
1 zz
= + −
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 3 Mã đề 388
A.
15
22
i
=+
. B.
16i
= − −
. C.
52i
=+
. D.
32i
=−
.
Câu 21: Cho hình chóp
.S ABCD
c đy
ABCD
là hình bình hành tâm
O
. Giao tuyến của hai mặt
phẳng
( )
SAB
và
( )
SCD
l đường thẳng no dưới đây?
A. Đường thẳng
SO
. B. Đường thẳng
AC
.
C. Đường thẳng đi qua
S
và song song
AB
. D. Đường thẳng đi qua
S
và song song với
AD
.
Câu 22: Hàm số no dưới đây đồng biển trên ?
A.
42
y x x=+
. B.
3
3y x x=+
. C.
21
3
x
y
x
+
=
+
. D.
3
y x x= − −
.
Câu 23: Biết rằng với mi giá tr thực của tham số
m
, cc đường thẳng
: ( 2) 2 3
m
d y m x m= − + −
cùng
đi qua một điểm cố đnh là
( ; )I a b
. Tính giá tr của biểu thc:
S a b=+
A.
3S =−
. B.
1S =−
. C.
1S =
. D.
3S =
.
Câu 24: Hàm số no dưới đây đồng biến trên khoảng
(0; )+
?
A.
3
logyx=
. B.
6
logyx
=
. C.
3
log
e
yx=
. D.
1
4
logyx=
.
Câu 25: Trong không gian với hệ ta độ
Oxyz
, cho mặt cầu
()S
c phương trình
2 2 2
4 2 4 0x y z x y+ + + − − =
.Tính bán kính
R
của
( ).S
A.
1
. B.
9
. C.
2
. D.
3
.
Câu 26: Điểm cực đại của hàm số
32
3 2019y x x= − +
là
A.
2019y =
. B.
(0;2019)M
. C.
0x =
. D.
2x =
.
Câu 27: Tập xc đnh của hàm số
cotyx=
là:
A.
\ 2 ,kk
. B.
\,
2
kk

+


.
C.
\,kk
. D.
\ 2 ,
2
kk

+


.
Câu 28: Trong không gian với hệ ta độ
Oxyz
, cho mặt phẳng
( )
: 1 0P x y z+ − − =
v đường thẳng
2 4 1
:
2 2 1
x y z
d
+ − +
==
−
. Viết phương trình đường thẳng
d
là hình chiếu vuông góc của
d
trên
( )
P
.
A.
21
:
7 5 2
x y z
d
++
==
−
. B.
21
:
7 5 2
x y z
d
−−
==
−
.
C.
21
:
7 5 2
x y z
d
++
==
. D.
21
:
7 5 2
x y z
d
−−
==
.
Câu 29: Trong mặt phẳng với hệ trục ta độ
Oxy
, cho hai điểm
( )
3;4A −
và
( )
5;6B
. Trung điểm của
đoạn thẳng
AB
có ta độ là
A.
( )
1;5
. B.
( )
4;1
. C.
( )
5;1
. D.
( )
8;2
.
Câu 30: Một nguyên hàm của hàm số
( )
2
3f x x=
là
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 4 Mã đề 388
A.
( )
3
F x x x=+
. B.
( )
3
1F x x=+
. C.
( )
6F x x=
. D.
( )
3
3F x x=
.
Câu 31: Cho tam giác
ABC
. Khẳng đnh no sau đây l sai?
A.
AB AC CB−=
. B.
0AB BA+=
. C.
AB AC BC−=
. D.
AB BC AC+=
.
Câu 32: Tập xc đnh của hàm số
( )
2
1
x
fx
x
=
−
là
A.
)
0; \ 1+
. B.
( )
1; +
. C.
)
0;1
. D.
\ 1;1−
.
Câu 33: Bảng biến thiên no dưới đây l của hàm số
2
22y x x= − + +
?
A.
x
+−
y
+
−
B.
x
1+− −
y
1−
−
−
C.
x
1+−
y
3
−
−
D.
x
1+−
y
+
+
3
Câu 34: Đạo hàm của hàm số
( )
2
sinf x x=
là:
A.
( )
' 2sinf x x=
. B.
( )
' 2cosf x x=
.
C.
( ) ( )
' sin 2f x x=−
. D.
( ) ( )
' sin 2f x x=
.
Câu 35: Tìm m để hàm số
2
4
2
()
2
2
x
khi x
fx
x
m khi x
−
−
=
+
=−
liên tục tại
2x =−
A.
4m =−
. B.
2m =
. C.
4m =
. D.
0m =
.
Câu 36: Tìm tất cả các giá tr của tham số m để đồ th của hàm số
39x
y
xm
−
=
+
có tiệm cận đng
A.
3m −
. B.
3m
. C.
3m =
. D.
3m =−
.
Câu 37: Tính
2019 2018
lim( 2 3 4)nn− + +
?
A.
−
. B.
+
. C.
2−
. D.
2019
.
Câu 38: Cho dãy số
( )
n
U
xc đnh bởi
1
*
1
2
5,
nn
u
u u n N
+
=
= +
Tính
10
u
?
A.
57
. B.
62
. C.
47
. D.
52
.
Câu 39: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
1 tan tan sin cot 4
2
x
x x x

+ + =


là
A.
6
−
. B.
2
. C.
6
. D.
2
−
.
Câu 40: Với
0; 1aa
, giá tr của biểu thc
log 5
a
a
là
A.
5
. B.
5
. C.
25
. D.
1
5
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 5 Mã đề 388
Câu 41: Cho hình chóp
.S ABC
có
6SA =
,
5SB =
,
4SC =
,
00
45 , 60ASB BSC ASC= = =
. Tính thể
tích khối chóp
.S ABC
.
A.
16V =
. B.
10V =
. C.
14V =
. D.
12V =
.
Câu 42: Bất phương trình
2
2 3 0xx− + +
có tập nghiệm là
A.
( ) ( )
; 1 3;− − +
. B.
( )
1;3−
. C.
1;3−
. D.
( )
3;1−
.
Câu 43: Khẳng đnh no sau đây l đúng?
A.
a b a c b c + +
. B.
22
a b a b
.
C.
a b ac bc
. D.
ab
ab
cc
.
Câu 44: Tính diện tích xung quanh của một hình nn c bn kính đy bằng
4cm
và chiều cao bằng
3cm
A.
2
20
xq
S cm
=
. B.
2
18
xq
S cm
=
. C.
2
15
xq
S cm
=
. D.
2
12
xq
S cm
=
.
Câu 45: Khối bát diện đều có bao nhiêu cạnh?
A.
1
. B.
8
.. C.
20
. D.
12
.
Câu 46: Mô đun của số phc
34zi=+
là
A.
4
. B.
7
. C.
3
. D.
5
Câu 47: Có bao nhiêu số tự nhiên có hai ch số mà cả hai ch số đ đều lẻ?
A.
20.
B.
50.
C.
25.
D.
45.
Câu 48: Cho hàm số
( )
fx
c đạo hàm trên v c đồ th của hàm
( )
y f x
=
đưc cho như hình vẽ.
Biết rằng
( ) ( ) ( ) ( )
3 0 4 1f f f f− + = + −
. Giá tr lớn nhất và giá tr nhỏ nhất của
( )
fx
trên
đoạn
3;4−
lần lưt là:
A.
(4)f
và
( 3)f −
. B.
( 3)f −
và
(0)f
. C.
(4)f
và
(0)f
. D.
(2)f
và
( 3)f −
.
Câu 49: Tìm tất cả các giá tr của tham số
m
để phương trình
2
2 1 0x x m− + − =
có hai nghiệm trái
dấu.
A.
2m
. B.
1m
. C.
1m
. D.
2m
.
Câu 50: Trong mặt phẳng với hệ ta độ
Oxy
, cho đường tròn
( ) ( )
2
2
: 2 36C x y+ + =
. Khi đ phép v tự
tỉ số
3k =
biến đường tròn
( )
C
thnh đường tròn
( )
'C
có bán kính là:
A.
108
. B.
12
. C.
6
. D.
18
.
Câu 51: Bất phương trình
( )
10xx−
có bao nhiêu nghiệm nguyên thuộc
1;2018−
?
A. 1. B. 2. C. 2019. D. 2018.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 6 Mã đề 388
Câu 52: Cho hình chóp
.S ABCD
c đy
ABCD
là hình bình hành tâm
O
. Gi
M
l trung điểm của
OB
,
( )
là mặt phẳng đi qua
M
, song song với
AC
và song song với
SB
. Thiết diện của
hình chóp
.S ABCD
khi cắt bởi mặt phẳng
( )
là hình gì?
A. Lục giác. B. Ngũ gic. C. Tam giác. D. T giác.
Câu 53: Trong không gian với hệ ta độ
Oxyz
, cho hai vectơ
( )
2;1; 2a =−
v vectơ
( )
1;0;2b =
.
Tìm ta độ vectơ
c
l tích c hướng của
a
và
b
.
A.
( )
2;6; 1c =−
. B.
( )
4;6; 1c =−
. C.
( )
4; 6; 1c = − −
. D.
( )
2; 6; 1c = − −
.
Câu 54: Phương trình
32xx−=
có bao nhiêu nghiệm nguyên?
A. 3. B. 0. C. 2. D. 1.
Câu 55: Nghiệm của phương trình
3
24
x−
=
thuộc tập no dưới đây?
A.
5;8
. B.
(
;0−
. C.
( )
0;5
. D.
( )
8;+
.
Câu 56:
n
u
đưc cho bởi công thc no dưới đây l số hạng tổng quát của một cấp số nhân?
A.
1
1
2
n
n
u
+
=
. B.
2
1
2
n
un=−
. C.
1
1
2
n
n
u =−
. D.
2
1
2
n
un=+
.
Câu 57: Cho tích phân
1
0
( 2) x
x
x e d a be− = +
, với
;ab
. Tổng
+ab
bằng
A.
1
. B.
−3
. C.
5
. D.
1−
.
Câu 58: Có bao nhiêu tiếp tuyến với đồ th hàm số
1
1
x
y
x
+
=
−
, biết tiếp tuyến đ song song với đường
thẳng
2x 7y = − +
?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 59: Hàm số no dưới đây l hm số lẻ?
A. . B. . C. . D. .
Câu 60: Trong không gian với hệ ta độ Oxyz, phương trình mặt phẳng trung trực của đoạn AB với
A. . B. . C. . D. .
Câu 61: Cho tích phân
1
0
( 2) x
x
x e d a be− = +
, với
;ab
. Tổng
+ab
bằng
A.
1
. B.
−3
. C.
5
. D.
1−
.
Câu 62: Có bao nhiêu tiếp tuyến với đồ th hàm số
1
1
x
y
x
+
=
−
, biết tiếp tuyến đ song song với đường
thẳng
2x 7y = − +
?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 63: Hàm số no dưới đây l hm số lẻ?
A. . B. . C. . D. .
44y x x= − − +
33y x x= − + +
yx=
2
51y x x= − +
( ) ( )
1, 3,2 , 1,5,4AB−−
4 7 0x y z− − + =
4 7 0x y z− − − =
4 18 0x y z− − − =
4 18 0x y z− − + =
44y x x= − − +
33y x x= − + +
yx=
2
51y x x= − +
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 7 Mã đề 388
Câu 64: Trong không gian với hệ ta độ Oxyz, phương trình mặt phẳng trung trực của đoạn AB với
A. . B. . C. . D. .
Câu 65: Tính tổng
1 2 3 2018
2018 2018 2018 2018
...S C C C C= + + + +
bằng.
A.
2018
2
. B.
2018
21−
. C.
2018
21+
. D.
2019
21−
.
Câu 66: Cho tam giác
ABC
có chu vi bằng 12 v bn kính đường tròn nội tiếp bằng 1. Diện tích của
tam giác
ABC
bằng
A.
12
. B.
3
. C.
6
. D.
24
.
Câu 67: Tính tích phân
2
0
(2 1)I x dx=+
A.
5I =
. B.
6I =
. C.
2I =
. D.
4I =
.
Câu 68: Tính diện tích hình phẳng giới hạn bởi đồ th hàm số
2
4y x x=−
và trục
Ox
A.
11
. B.
34
3
. C.
31
3
. D.
32
3
.
Câu 69: Cho các số phc
z
thỏa mãn
25z =
. Biết rằng trong mặt phẳng ta độ cc điểm biểu diễn
của số phc
( )
2w i i z= + −
cùng thuộc một đường tròn cố đnh. Tính bán kính
r
của đường
tròn đ?
A.
5r =
. B.
10r =
. C.
20r =
. D.
25r =
.
Câu 70: Phủ đnh của mệnh đề “
2
:0xx
” l mệnh đề no sau đây?
A.
2
:0xx
. B.
2
:0xx
. C.
2
:0xx
. D.
2
:0xx
.
Câu 71: Trong mặt phẳng với hệ ta độ
Oxy
, nếu phép tnh tiến theo vectơ
v
biến điểm
(1;2)A
thành
điểm
(1; 6)B −
thì nó biến đường thẳng
:2 3 0d x y− + =
thnh đường thẳng
'd
c phương trình
A.
2 3 0xy− − =
. B.
20xy−=
. C.
2 8 0xy− − =
. D.
2 5 0xy− − =
.
Câu 72: Cho hàm số
()y f x=
có tập xc đnh là
\1
và liên tục trên mỗi khoảng xc đnh của nó.
Biết
()fx
có bảng biến thiên như sau
Số nghiệm của phương trình
( ) 6fx=
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 73: Xét trong không gian, mệnh đề no dưới đây l đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
( ) ( )
1, 3,2 , 1,5,4AB−−
4 7 0x y z− − + =
4 7 0x y z− − − =
4 18 0x y z− − − =
4 18 0x y z− − + =
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 8 Mã đề 388
B. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với
đường thẳng còn lại.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng th ba thì song song với
nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng th ba thì vuông góc với
nhau.
Câu 74: Phép quay góc
0
90
biến đường thẳng
d
thnh đường thẳng
'd
. Khi đ
A.
'd
song song với
d
. B.
'd
trùng
d
.
C.
'd
tạo với
d
góc
0
60
D.
'd
vuông góc với
d
.
Câu 75: Trong mặt phẳng ta độ điểm biểu diễn số phc
z
thỏa mãn
1 2 3zi− − =
là
A. đường tròn tâm
(1;2)I
, bán kính
9R =
. B. đường tròn tâm
(1;2)I
, bán kính
3R =
.
C. đường tròn tâm
( 1; 2)I −−
, bán kính
3R =
. D.
đường thẳng c phương trình
2 3 0xy+ − =
.
Câu 76: Trong khai triển của biểu thc
8
2
1
2.x
x

−


Hệ số của
7
x
là:
A.
112
. B.
112−
. C.
1792−
. D.
1792
.
Câu 77: Để lấy nước tưới cây, ông Tráng cần xây một bể cha nước có dạng hình hộp ch nhật không
có nắp đậy. Nếu bể cần có thể tích
3
50m
và chiều dài gấp 4 lần chiều rộng thì chiều cao bằng
bao nhiêu để chi phí vật liệu thấp nhất.
A.
4,5m
. B. 5m.
C.
2,5m
. D.
2m
Câu 78: Trong mặt phẳng với hệ ta độ
Oxy
cho đường thẳng
:2 3 4 0d x y− + =
. Vectơ no sau đây l
một vectơ chỉ phương của d.
Câu 79: Cho
tan 2a =
. Tính giá tr biểu thc
2sin cos
sin cos
aa
P
aa
−
=
+
.
A.
2P =
. B.
1P =
. C.
5
3
P =
. D.
1P =−
.
Câu 80: Khẳng đnh no sau đây l sai?
A.
( )
sin sin

− = −
. B.
( )
cot cot

− = −
. C.
( )
cos cos

− = −
. D.
( )
tan tan

− = −
.
Câu 81: Trong mặt phẳng với hệ ta độ
Oxy
, cho đường thẳng
: 4 15 0d x y− + =
v điểm
( )
2; 0A
.
Tìm ta độ điểm
M
thuộc
d
để đoạn
AM
c độ dài nhỏ nhất.
A.
( )
15; 0M −
. B.
( )
5; 5M
. C.
( )
0; 3M
. D.
( )
1;4M
.
Câu 82: Thể tích khối lăng trụ tam gic đều có tất cả các cạnh đều bằng
a
là
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
2
12
a
. D.
3
2
4
a
.
Câu 83: Cho t diện đều
ABCD
c độ di cạnh bằng
a
. Tính tích vô hướng của hai vectơ
AB
v
CD
.
A.
.0AB CD =
. B.
2
.AB CD a=
. C.
2
.
2
a
AB CD =
. D.
2
.AB CD a=−
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 9 Mã đề 388
Câu 84: Một hộp đựng 9 quả cầu đưc đnh số lần lưt từ 1 đến 9. Lấy ngu nhiên một quả cầu từ hộp
đ. Tính xc suất lấy đưc quả cầu mang số chn.
A.
2
3
. B.
5
9
. C.
4
5
. D.
4
9
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 10 Mã đề 388
Tuonganh0209@gmail.com
Câu 1: Trong mặt phẳng với hệ trục
Oxy
, cho hai đường tròn
( ) ( )
2
2
: 1 4C x y− + =
và
( ) ( ) ( )
22
: 4 3 16C x y
− + − =
cắt nhau tại hai điểm phân biệt
A
và
B
. Lập phương trình đường
thẳng
AB
A.
20xy+ − =
. B.
2. 0xy− + =
C.
20xy+ + =
. D.
20xy− − =
.
Lời giải
Tác giả: Nguyễn Ngọc Thảo, FB: Nguyễn Ngọc Thảo
Chọn A.
Cách 1: Xét hệ
( )
( ) ( )
2
2
22
22
22
14
2 3 0
8 6 9 0
4 3 16
xy
x y x
x y x y
xy
− + =
+ − − =

+ − − + =
− + − =
( )
2
2
2
3 7 1 7
,
2
2
22
2 6 1 0
2 2 3 0
3 7 1 7
,
22
xy
yx
yx
xx
x x x
xy
+−
==
=−
=−

− + =
+ − − − =
−+
==
Suy ra
3 7 1 7
,
22
A

+−



,
3 7 1 7
,
22
B

−+



.
SỞ GD&ĐT BẮC GIANG
HỘI ĐỒNG KTKT GIÁO VIÊN
NĂM HỌC 2018 - 2019
------------------
ĐỀ THI TRẮC NGHIỆM
MÔN TOÁN THPT
Thời gian làm bài: 90 phút (80 câu trắc nghiệm)
MÃ ĐỀ: 385
(Giáo viên không được sử dụng tài liệu)
Họ tên giáo viên: ............................................................................... Ngày sinh: ................. SBD: .................
Trường: ......................................................................................... .... Huyện / thành phố: ...............................
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 11 Mã đề 388
( )
C
có tâm
( )
1;0O
,
( )
C
có tâm
( )
4;3O
( )
3;3OO
=
Nên đường thẳng
AB
qua
A
và nhận
( )
1;1n
là vécto pháp tuyến.
Phương trình:
3 7 1 7
1 1 0 2 0
22
x y x y
+−
− + − = + − =
. Chn
A
.
Cách 2: Giả sử hai đường tròn
( ) ( )
2
2
: 1 4C x y− + =
và
( ) ( ) ( )
22
: 4 3 16C x y
− + − =
cắt nhau
tại hai điểm phân biệt
A
và
B
khi đ ta độ của
A
và thỏa mãn hệ phương trình:
( )
( ) ( )
2
2
22
22
22
14
2 3 0 (1)
8 6 9 0 (2)
4 3 16
xy
x y x
x y x y
xy
− + =
+ − − =

+ − − + =
− + − =
Lấy
(1)
trừ
(2)
ta đưc:
6 6 12 0 2 0x y x y+ − = + − =
l phương trình đường thẳng đi qua 2
điểm
A
và
B
Câu 2: Một hình trụ có diện tích xung quanh bằng
16
và thiết diện qua trục của hình trụ này là một
hình vuông. Thể tích
V
A.
32 2
. B.
18
. C.
16
. D.
24
.
Lời giải
Tác giả: Nguyễn Ngọc Thảo, FB: Nguyễn Ngọc Thảo
Chọn C.
Ta có diện tích xung quanh:
2 16
xq
S Rl

==
Thiết diện qua trục là một hình vuông nên:
2l R h==
22
2 16 2 .2 4 2
xq
S Rl R R R
= = = = =
Thể tích khối trụ là:
2 2 2
. . .2 .2 .2.2 16V R h R R
= = = =
. Chn
C
.
buichithanh1987@gmail.com
Câu 3: Một cấp số cộng gồm
5
số hạng. Hiệu số hạng đầu và số hạng cuối bằng
20
. Tìm công sai
d
của cấp số cộng đã cho
A.
5d =−
. B.
4d =
. C.
4d =−
. D.
5d =
.
Lời giải
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 12 Mã đề 388
Tác giả: Bùi Chí Thanh, FB: Thanh bui
Chọn C.
Gi năm số hạng của cấp số cộng đã cho l:
1 2 3 4 5
; ; ; ; .uuuuu
Theo đề bài ta có:
1 5 1 1
20 ( 4 ) 20 5u u u u d d− = − + = = −
Câu 4: Với hai véc tơ không cùng phương
a
và
b
. Xét hai véc tơ
23u a b=−
và
( 1)v a x b= + −
. Tìm
x để
u
và
v
cùng phương.
A.
3
2
x =
. B.
1
2
x =
. C.
1
2
x =−
. D.
3
2
x =−
.
Lời giải
Tác giả: Bùi Chí Thanh, FB: Thanh bui
Chọn B.
Do hai véc tơ
a
và
b
không cùng phương nên điều kiện để hai véc tơ
23u a b=−
và
( 1)v a x b= + −
cùng phương l:
2
2 .1
1
3 .( 1)
2
k
k
u kv
kx
x
=
=
=

− = −
=−
kenbincuame@gmail.com
Câu 5: Gi tr lớn nhất của hm số
2sin 1yx=+
l
A.
1−
. B.
1
. C.
1
2
−
. D.
3
.
Lời giải
Tác giả: Nguyễn Vit Thảo, FB: Vit Thảo
Chọn D.
Vì
sin 1x
,
x
nên
2sin 1 3yx= +
,
x
.
3y =
khi
sin 1x =
2
2
xk
= +
,
( )
k
.
Vậy gi tr lớn nhất của hm số
2sin 1yx=+
l
3
.
Câu 6: Cho t diện ABCD. Gi
M
,
N
lần lưt l trung điểm của
BC
,
AD
. Biết
2AB a=
,
22CD a=
v
5.MN a=
Số đo gc gia hai đường thẳng
AB
v
CD
l
A.
60
. B.
30
. C.
90
. D.
45
.
Lời giải
Tác giả: Nguyễn Vit Thảo, FB: Vit Thảo
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 13 Mã đề 388
Chọn D.
Ta c:
MN MB BA AN= + +
v
MN MC CD DN= + +
. Suy ra
( ) ( ) ( )
2MN MB MC BA CD AN DN BA CD= + + + + + = +
(Vì
M
l trung điểm
BC
v
N
l
trung điểm
AD
).
Khi đ:
2 2 2
4 2 .MN BA CD BACD= + +
(
)
2 2 2
2
1
. 4 4
2
BACD MN BA CD a = − − =
.
Do vậy ta c:
( )
.
2
cos ,
2
.
BACD
AB CD
BA CD
==
.
Vậy, số đo gc gia hai đường thẳng
AB
v
CD
l
45 .
hungvn1985@gmail.com
Câu 7: Điều kiện xc đnh của phương trình
28xx− = −
là
A.
2;8x
. B.
8x
. C.
2x
. D.
8x
.
Lời giải
Tác giả: Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn C.
ĐK:
2 0 2xx−
Câu 8: Mẹ hơn Minh
25
tuổi. Biết rằng
4
năm về trước tuổi của mẹ gấp
6
lần tuổi của Minh. Hãy
tính tuổi của Minh hiện nay.
A. 9 tuổi. B. 5 tuổi. C. 8 tuổi. D. 10 tuổi.
Lời giải
Tác giả: Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn A.
Gi tuổi hiện nay của Minh là
x
,
( )
0x
. Khi đ hiện nay tuổi của mẹ là
25 x+
.
Do
4
năm về trước tuổi của mẹ gấp
6
lần tuổi Minh nên ta có
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 14 Mã đề 388
25 4 6( 4) 9.x x x+ − = − =
Vậy Minh hiện nay là
9
tuổi.
Phamquoctoan87@gmail.com
Câu 9: Gi
1
x
,
2
x
là hai nghiệm của phương trình
2
22
log 3log 2 0xx− + =
. Tính
12
P x x=+
.
A.
6
. B.
3−
. C.
2
. D.
3
.
Lời giải
Tác giả: Phạm Quốc Toàn, FB: Phạm Quốc Toàn
Chọn A.
2
22
log 3log 2 0xx− + =
21
22
log 1 2
log 2 4
xx
xx
==



==

.
Vậy
12
2 4 6P x x= + = + =
.
Phamquoctoan87@gmail.com
Câu 10: Cho hàm số
32
3 2 1y x x x= − − −
c đồ th
( )
C
. Phương trình tiếp tuyến với
( )
C
tại giao điểm
của
( )
C
với trục tung là
A.
21yx= − −
. B.
21yx=−
. C.
21yx=+
. D.
21yx= − +
.
Lời giải
Tác giả: Phạm Quốc Toàn, FB: Phạm Quốc Toàn
Chọn A.
Ta có
2
3 6 2y x x
= − −
.
Đồ th
( )
C
cắt trục tung tại điểm
( )
0; 1M −
.
Phương trình tiếp tuyến với
( )
C
tại
( )
0; 1M −
là
( ) ( ) ( )
0 0 1y y x
= − + −
21yx = − −
.
phuongthu081980@gmail.com
Câu 11: Trong mặt phẳng với hệ trục ta độ , cho hai vectơ
và
.
Khẳng
đnh no sau đây l đúng?
A. và
cùng hướng
.
B. và
ngưc hướng.
C. . D. .
Lời giải
Tác giả:Nguyễn Thị Phương Thu, FB: Nguyễn Phương Thu
Chọn B.
Ta có
( )
2 2; 1 2a i j a b a= − = − = −
( )
;,O i j
2a i j=−
( )
4;2b =−
a
b
a
b
( )
1;2a =−
( )
2;1a =
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 15 Mã đề 388
và
ngưc hướng.
Câu 12: Cho hình chóp
.S ABCD
c đy
ABCD
là hình ch nhật, và
. Gi
M
l trung điểm của cạnh .
Khoảng cách từ
M
đến mặt phẳng bằng:
A.
B. C. D.
Lời giải
Tác giả:Nguyễn Thị Phương Thu, FB: Nguyễn Phương Thu
Chọn B.
Cách 1: S
K G M
A D
H O
B C
Ta dựng:
a
b
( )
, 2 ,AB a AD a SA ABCD= = ⊥
SA a=
SC
( )
SBD
.
2
a
.
3
a
4
.
3
a
2
.
3
a
,
,
AH DB H DB
AK SH K SH
⊥
⊥
( )
( )
( ) ( ) ( )
( )
,,
SA ABCD SA BD
BD SAH BD AK
AH BD
AK BD
AK SBD K SBD d A SBD AK
AK SH
⊥ ⊥
⊥ ⊥
⊥
⊥
⊥ =
⊥
( )
2
2 2 2 2 2
2 2 2 2 2 2
1 1 1 1 1 5
:
4
2
1 1 1 5 1 9 2
:
4 4 3
ABD
AH AB AD a a
a
a
AHK AK
AK AH AS a a a
= + = + =
= + = + = =
1
):
2
MG
SAC AM SO G
AG
+ = =
( )
( )
( )
( )
( )
( )
( )
,
1
2
,
1 1 2
,.
2 2 3 3
d M SBD
MG
AM SBD G
AG
d A SBD
aa
d M SBD AK
= = =
===
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 16 Mã đề 388
Cách 2: z
S
M
A D y
O
B C
x
Chn hệ trục ta độ như hình vẽ:
( ) ( ) ( ) ( ) ( )
( ) ( )
( )
2 2 2
0;0;0 , ;0;0 , ;2 ;0 ; 0;2 ;0 , 0;0; ; ;
22
;0; ; 0; 2 ; ; 2 ; ;2
aa
A B a C a a D a S a M a
BS a a DS a a BS DS a a a




= − = − =

Suy ra VTPT của
()SBD
là v phương trình mp
()SBD
là:
( ) ( ) ( )
( )
( )
2 2 2
2 0 2 0 0 2 2 2 0
2. 2. 2
22
,
3
2 1 2
x a y z x y z a
aa
aa
a
d M SBD
− + − + − = + + − =
+ + −
= =
++
Thutrangtc1@gmail.com
Câu 13: Biết
(
)
2
lim 4 1 1
x
x ax bx
→−
+ + + = −
. Tính giá của biểu thc
23
2P a b=−
.
A.
32P =
. B.
0P =
. C.
16P =
. D.
8P =
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang, FB: Nguyễn Thị Thu Trang
Chọn D.
TH1:
2b =
(
)
2
2
2
1
1
lim 4 1 2 lim lim .
4
1
4 1 2
42
x x x
a
ax a
x
x ax x
a
x ax x
xx
→− →− →−
+
+
+ + + = = = −
+ + −
− + + −
(
)
2
lim 4 1 1 1 4
4
x
a
x ax bx a
→−
+ + + = − − = − =
.
TH2:
2b
(
)
2
2
neáu b > 2
1
lim 4 1 lim 4
neáu b < 2
xx
a
x ax bx x b
xx
→− →−


−
+ + + = − + + + =



+



Vậy
23
4, 2 2 0a b P a b= = = − =
.
( )
2;1;2n =
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 17 Mã đề 388
Câu 14: Xếp
6
hc sinh gồm
3
hc sinh nam và
3
hc sinh ngồi vào hai dãy ghế đối diện nhau, mỗi
dãy có
3
ghế (mỗi hc sinh ngồi một ghế, các ghế đều khác nhau). Hỏi có bao nhiêu cách xếp
sao cho không có hai hc sinh cùng giới ngồi đối diện nhau.
A. 720. B. 36. C. 288. D. 72.
Lời giải
Tác giả: Nguyễn Thị Thu Trang, FB: Nguyễn Thị Thu Trang
Chọn D.
Xếp chỗ ngồi cho bạn nam th nhất có
6
cách xếp.
Xếp chỗ ngồi cho bạn nam th hai có 4cách xếp (Trừ chỗ của bạn th nhất và ghế đối diện).
Xếp chỗ ngồi cho bạn nam th ba có
2
cách xếp.
Xếp chỗ ngồi cho
3
bạn n có
3! 6=
cách xếp (3 bạn n xếp ngu nhiên vào 3 chỗ còn lại).
Vậy có
6.4.2.6 288=
cách xếp chỗ ngồi cho 6 bạn thỏa mãn yêu cầu bài toán.
ptpthuyedu@gmail.com
Câu 15: Cho hình chóp
.S ABCD
c đy l hình vuông cạnh
a
,
SAB
l tam gic đều và nằm trong mặt
phẳng vuông góc với đy. Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp
.S ABCD
A.
2
3Sa
=
. B.
2
4
3
a
S
=
. C.
2
7
3
a
S
=
. D.
2
7Sa
=
.
Lời giải
Tác giả: Phạm Thị Phương Thúy, FB: thuypham
Chọn C.
+) Xác định mặt cầu ngoại tiếp hình chóp
.S ABCD
Gi SH l đường cao của tam giác SAB. Vì SAB l tam gic đều và nằm trong mặt phẳng vuông
góc với mặt đy nên SH l đường cao của hình chóp S.ABCD.
Gi O là tâm của hình vuông ABCD, từ O dựng
()Ox ABCD⊥
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 18 Mã đề 388
Từ trng tâm G của tam giác SAB dựng
()Gy SAB⊥
.
Gi
I Ox Gy=
. Vậy I là tâm của mặt cầu ngoại tiếp hình chóp
.S ABCD
.
+) Chứng minh I là tâm mặt cầu cần tìm
Vì
I Ox
, mà
()Ox ABCD⊥
, O là tâm hình vuông ABCD nên I cch đều A, B, C, D (1).
Mặt khác G là trng tâm của tam gic đều SAB,
I Gy
, mà
()Gy SAB⊥
nên I cch đều S, A, B
(2).
Từ (1) và (2) suy ra I cch đều S, A, B, C, D. Nên I là tâm mặt cầu ngoại tiếp hình chóp
S.ABCD, bán kính R=IB
+) Tìm độ dài bán kính mặt cầu
Vì
()OI ABCD⊥
,
()SH ABCD⊥
nên
//OI GH
vì
G SH
(3)
Mặt khác
()Gy SAB⊥
,
I Gy
mà
()OH SAB⊥
(vì
,OH AB OH SH⊥⊥
) nên
/ /OGI H
(4)
Từ (3) và (4) suy ra GHOI là hình bình hành
1 1 3 3
..
3 3 2 6
aa
OI GH SH= = = =
Vì
()OI ABCD OI OB BOI⊥ ⊥
vuông tại B
Xét
BOI
vuông tại B ta có
22
2 2 2 2
3 2 7 21
6 2 12 6
aa
IB IO OB a IB a R
= + = + = = =
.
Diện tích mặt cầu là
22
7
4.
3
S R a

==
ptpthuyedu@gmail.com
Câu 16: Tìm x để hai vectơ
( ;2)ax=
và
(2; 3)b =−
có giá vuông góc với nhau.
A. 3. B. 0. C.
3−
. D. 2.
Lời giải
Tác giả: Phạm Thị Phương Thúy, FB: thuypham
Chọn A.
Vectơ
( ;2)ax=
và
(2; 3)b =−
có giá vuông góc với nhau
. 0 2 6 0 3a b x x = − = =
Vậy
3x =
.
kimoanh0102@gmail.com
Câu 17: Trong mặt phẳng với hệ ta độ Oxy, cho elip
( )
22
:1
25 9
xy
E +=
. Tiêu cự của (E) bằng
A. 10. B. 16. C. 4. D. 8.
Lời giải
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 19 Mã đề 388
Tác giả:Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh
Chọn D.
Phương trình chính tắc của elip có dạng:
( )
22
22
1 0, 0
xy
ab
ab
+ =
.
Do đ elip (E) có
22
5
4
3
a
c a b
b
=
= − =
=
.
Tiêu cự của elip (E) bằng
28c =
.
Câu 18: Cho hai tập hp
)
1;3A =−
và
1;5B =
. Giao của A và B là tập hp no sau đây?
A.
1;5−
. B.
)
1;3
. C.
1;3
. D.
1;2
.
Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh
Chọn B.
)
)
1;3 1;5 1;3AB = − =
.
Quachthuy.tranphu@gmail.com.
Câu 19: Biết các nghiệm của phương trình
1
cos2
2
x =−
có dạng
xk
m
=+
và
xk
n
= − +
,
k
;
với
,mn
là các số nguyên dương. Khi đ
mn+
bằng
A. 4. B. 3. C. 5. D. 6.
Lời giải
Tác giả: Quách Phương Thúy, FB: Phương Thúy
Chọn D.
1
cos2
2
x =−
( )
2
22
2
33
cos2 cos
2
3
22
33
x k x k
xk
x k x k





= + = +

=


= − + = − +


3 3 6mn + = + =
.
Câu 20: Cho số phc
12zi=−
. Tìm số phc
2
1 zz
= + −
.
A.
15
22
i
=+
. B.
16i
= − −
. C.
52i
=+
. D.
32i
=−
.
Lời giải
Tác giả: Quách Phương Thúy, FB: Phương Thúy
Chọn C.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 20 Mã đề 388
12zi=−
( )
2
2
1 2 3 4z i i = − = − −
1 1 2 3 4 5 2i i i
= + − + + = +
Phản biện: Email: Dangvanquanggb1@gmail.com - FB: DangQuang
trichinhsp@gmail.com
Câu 21: Cho hình chóp
.S ABCD
c đy
ABCD
là hình bình hành tâm
O
. Giao tuyến của hai mặt
phẳng
( )
SAB
và
( )
SCD
l đường thẳng no dưới đây?
A. Đường thẳng
SO
. B. Đường thẳng
AC
.
C. Đường thẳng đi qua
S
và song song
AB
. D. Đường thẳng đi qua
S
và song song với
AD
.
Lời giải
Tác giả: Nguyễn Trí Chính, FB: Nguyễn trí Chính
Chọn C.
Có
( ) ( )
AB CD
Sx AB CD
SAB SDC Sx
=
. Chn C
Câu 22: Hàm số no dưới đây đồng biển trên ?
A.
42
y x x=+
. B.
3
3y x x=+
. C.
21
3
x
y
x
+
=
+
. D.
3
y x x= − −
.
Lời giải
Tác giả: Nguyễn Trí Chính, FB: Nguyễn trí Chính
Chọn B.
42
y x x=+
có
.0ab
nên có
1
cực tr (loại)
21
3
x
y
x
+
=
+
c TXĐ
\3D =−
(loại)
3
y x x= − −
có
0a
(loại)
3
3y x x=+
, TXĐ
D =
Có
/2
3 3 0,y x x= +
. Suy ra
3
3y x x=+
luôn đồng biển trên
C
B
D
A
S
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 21 Mã đề 388
nvthang368@gmail.com
Câu 23: Biết rằng với mi giá tr thực của tham số
m
, cc đường thẳng
: ( 2) 2 3
m
d y m x m= − + −
cùng
đi qua một điểm cố đnh là
( ; )I a b
. Tính giá tr của biểu thc:
S a b=+
A.
3S =−
. B.
1S =−
. C.
1S =
. D.
3S =
.
Lời giải
Tác giả: Nguyễn Văn Thắng, Facebook: Nguyễn Thắng
Chọn B.
Ta c phương trình của đường thẳng đã cho:
: ( 2) 2 3 ( 2) 2 3
m
d y m x m x m x= − + − = + − −
Vì cc đường thẳng
m
d
luôn đi qua điểm I nên ta tìm x để m b triệt tiêu ⇒
( 2; 1) 1IS− = −
⇒ Chn B
nvthang368@gmail.com
Câu 24: Hàm số no dưới đây đồng biến trên khoảng
(0; )+
?
A.
3
logyx=
. B.
6
logyx
=
. C.
3
log
e
yx=
. D.
1
4
logyx=
.
Lời giải
Tác giả: Nguyễn Văn Thắng, Facebook: Nguyễn Thắng
Chọn A.
Hàm số
log
a
yx=
đồng biến trên khoảng
(0; )+
⇔
1a
⇒ Chn A
tranquocan1980@gmail.com
Câu 25: Trong không gian với hệ ta độ
Oxyz
, cho mặt cầu
()S
c phương trình
2 2 2
4 2 4 0x y z x y+ + + − − =
.Tính bán kính
R
của
( ).S
A.
1
. B.
9
. C.
2
. D.
3
.
Lời giải
Tác giả:Trần Quốc An, FB: TranQuocAn
Chọn D.
Giả sử phương trình mặt cầu
2 2 2 2 2 2
( ): 2 2 2 0 ( 0)S x y z ax by cz d a b c d+ + − − − + = + + −
Ta có:
2, 1, 0, 4a b c d= − = = = −
Bán kính
2 2 2
3R a b c d= + + − =
.
Câu 26: Điểm cực đại của hàm số
32
3 2019y x x= − +
là
A.
2019y =
. B.
(0;2019)M
. C.
0x =
. D.
2x =
.
Lời giải
Tác giả:Trần Quốc An, FB: TranQuocAn
Chọn C.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 22 Mã đề 388
Ta có:
2
0
3 6 0
2
x
y x x
x
=
= − =
=
Bảng biến thiên:
x
−
0
2
+
()fx
+
0
−
0
+
()fx
2019
+
2015
−
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực đại tại điểm
0.x =
Thuyhung8587@gmail.com
Câu 27: Tập xc đnh của hàm số
cotyx=
là:
A.
\ 2 ,kk
. B.
\,
2
kk

+


.
C.
\,kk
. D.
\ 2 ,
2
kk

+


.
Lời giải
Tác giả: Cấn Vit Hưng, FB: Viet Hung
Chọn C.
+)Điều kiện:
sin 0 ,x x k k
, suy ra tập xc đnh của hàm số
cotyx=
là
\,D k k
=
.
Thuyhung8587@gmail.com
Câu 28: Trong không gian với hệ ta độ
Oxyz
, cho mặt phẳng
( )
: 1 0P x y z+ − − =
v đường thẳng
2 4 1
:
2 2 1
x y z
d
+ − +
==
−
. Viết phương trình đường thẳng
d
là hình chiếu vuông góc của
d
trên
( )
P
.
A.
21
:
7 5 2
x y z
d
++
==
−
. B.
21
:
7 5 2
x y z
d
−−
==
−
.
C.
21
:
7 5 2
x y z
d
++
==
. D.
21
:
7 5 2
x y z
d
−−
==
.
Lời giải
Tác giả: Cấn Vit Hưng, FB: Viet Hung
Chọn B.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 23 Mã đề 388
+) Phương trình tham số của
22
: 4 2
1
xt
d y t
zt
= − +
=−
= − +
,
tR
. Gi
( )
2 2 ;4 2 ; 1M t t t= − + − − +
là giao
điểm của
d
và
( )
P
( ) ( ) ( )
2 2 4 2 1 1 0t t t − + + − − − + − =
2t=
( )
2;0;1M=
.
+) Mặt phẳng
( )
P
có 1 vector pháp tuyến là
( )
1;1; 1
P
n =−
. Điểm
( )
0;2;0N =
d
.
Gi
l đường thẳng qua
( )
0;2;0N
và vuông góc với mặt phẳng
( )
P
nhận vector
( )
1;1; 1
P
n =−
làm vector chỉ phương. Suy ra phương trình của
là:
( ) ( )
0 2 0
: : 2
1 1 1
xc
x y z
yc
zc
=
− − −
= = = +
−
=−
,
cR
. Gi
( )
;2 ;M c c c
= + −
l giao điểm của
với mặt phẳng
( )
P
( ) ( )
1
2 1 0
3
c c c c + + − − − = = −
1 5 1
;;
333
M

−


.
+)
7 5 2
;;
3 3 3
MM
= − −


, đường thẳng
d
là hình chiếu vuông góc của
d
trên mặt phẳng
( )
P
nên
d
chính l đường thẳng
'MM
, suy ra
d
đi qua
( )
2;0;1M
và nhận vector
( )
3 7; 5;2u MM
= − = −
làm vector chỉ phương nên phương trình của
d
là:
21
:
7 5 2
x y z
d
−−
==
−
.
luongthanh80tm@gmail.com
Câu 29: Trong mặt phẳng với hệ trục ta độ
Oxy
, cho hai điểm
( )
3;4A −
và
( )
5;6B
. Trung điểm của
đoạn thẳng
AB
có ta độ là
A.
( )
1;5
. B.
( )
4;1
. C.
( )
5;1
. D.
( )
8;2
.
Lời giải
Tác giả: Nguyễn Lương Thành, FB: Luong Thanh Nguyen
Chọn A.
d'
d
P
M
N
M'
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 24 Mã đề 388
Gi
I
l trung điểm của đoạn thẳng
AB
. Khi đ ta có:
35
1
22
46
5
22
AB
I
AB
I
xx
x
yy
y
+
−+
= = =
+
+
= = =
( )
1;5I
.
Câu 30: Một nguyên hàm của hàm số
( )
2
3f x x=
là
A.
( )
3
F x x x=+
. B.
( )
3
1F x x=+
. C.
( )
6F x x=
. D.
( )
3
3F x x=
.
Lời giải
Tác giả: Nguyễn Lương Thành, FB: Luong Thanh Nguyen
Chọn B.
Ta có:
( )
23
3f x dx x dx x C= = +

với
C
là một hằng số.
Do đ cc phương n A, C, D b loại.
Ta chn phương n B (trong trường hp
1C =
).
vannguyen30031981@gmail.com
Câu 31: Cho tam giác
ABC
. Khẳng đnh no sau đây l sai?
A.
AB AC CB−=
. B.
0AB BA+=
. C.
AB AC BC−=
. D.
AB BC AC+=
.
Lời giải
Tác giả: Nguyễn Thị Vân, FB: Vân Nguyễn Thị
Chọn C.
Theo quy tắc về hiệu hai véc tơ ta c:
AB AC CB−=
nên khẳng đnh C sai.
Câu 32: Tập xc đnh của hàm số
( )
2
1
x
fx
x
=
−
là
A.
)
0; \ 1+
. B.
( )
1; +
. C.
)
0;1
. D.
\ 1;1−
.
Lời giải
Tác giả: Nguyễn Thị Vân, FB: Vân Nguyễn Thị
Chọn A.
Điều kiện xc đnh:
2
0
0
0
1
1
10
1
x
x
x
x
x
x
x
−
−
Vậy tập xc đnh của hàm số là
)
0; \ 1 .+
hanhkeo@gmail.com
Câu 33: Bảng biến thiên no dưới đây l của hàm số
2
22y x x= − + +
?
A.
B.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 25 Mã đề 388
x
+−
y
+
−
x
1+− −
y
1−
−
−
C.
x
1+−
y
3
−
−
D.
x
1+−
y
+
+
3
Lời giải
Tác giả: Nguyễn Hồng Hạnh, FB: Nguyễn Hồng Hạnh
Chọn C.
' 2 2yx= − +
' 0 1yx= =
Hàm số đồng biến trên
( )
;1−
; nghch biến trên
( )
1; +
. Chn C.
hanhkeo@gmail.com
Câu 34: Đạo hàm của hàm số
( )
2
sinf x x=
là:
A.
( )
' 2sinf x x=
. B.
( )
' 2cosf x x=
.
C.
( ) ( )
' sin 2f x x=−
. D.
( ) ( )
' sin 2f x x=
.
Lời giải
Tác giả: Nguyễn Hồng Hạnh, FB: Nguyễn Hồng Hạnh
Chọn D.
( ) ( )
' 2sin . sin ' 2sin .cos sin2f x x x x x x= = =
. Chn D.
nongdansanhdieu.tk@gmail.com
Câu 35: Tìm m để hàm số
2
4
2
()
2
2
x
khi x
fx
x
m khi x
−
−
=
+
=−
liên tục tại
2x =−
A.
4m =−
. B.
2m =
. C.
4m =
. D.
0m =
.
Lời giải
Tác giả: Nguyễn Tuấn Đạt, FB: Nguyễn Đạt
Chọn A.
Hàm số liên tục tại
2x =−
khi và chỉ khi
2
22
4
lim lim 4
2
xx
x
m m m
x
→− →−

−
= = = −

+

Chọn A.
nongdansanhdieu.tk@gmail.com
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 26 Mã đề 388
Câu 36: Tìm tất cả các giá tr của tham số m để đồ th của hàm số
39x
y
xm
−
=
+
có tiệm cận đng
A.
3m −
. B.
3m
. C.
3m =
. D.
3m =−
.
Lời giải
Tác giả: Nguyễn Tuấn Đạt, FB: Nguyễn Đạt
Chọn A.
Tập xc đnh
\Dm=−
Dễ dàng chn đưc A
Giachuan85@gmail.com
Câu 37: Tính
2019 2018
lim( 2 3 4)nn− + +
?
A.
−
. B.
+
. C.
2−
. D.
2019
.
Lời giải:
H và tên: Trần Gia Chuân
Chọn A.
Ta có
( )
2019 2018 2019
2019
.
34
lim 2 3 4 lim 2n n n
nn


− + + = − + + = −




.
Câu 38: Cho dãy số
( )
n
U
xc đnh bởi
1
*
1
2
5,
nn
u
u u n N
+
=
= +
Tính
10
u
?
A.
57
. B.
62
. C.
47
. D.
52
.
Lời giải:
H và tên: Trần Gia Chuân
Chọn C.
Cách 1 : Dùng casio 570VN
B1 : Nhập vo my tính “2”=>SHIFT=>STO=>A
B2: Nhập
5:B A A B= + =
B3: Ấn CALC rồi bấm liên tiếp dấu “=” cho kết quả
10
47u =
.
Cách 2 : Từ
1
*
1
2
5,
nn
u
u u n N
+
=
= +
.
Ta có
1
5
nn
uu
+
−=
nên dãy
( )
n
U
là một cấp số cộng với công sai
5d =
nên
10 1
9 2 45 47u u d= + = + =
.
cvtung.lg2@bacgiang.edu.vn
Câu 39: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
1 tan tan sin cot 4
2
x
x x x

+ + =


là
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 27 Mã đề 388
A.
6
−
. B.
2
. C.
6
. D.
2
−
.
Lời giải
Tác giả: Cao Văn Tùng, FB: Cao Tung
Chọn D.
Điều kiện
cos 0
sin2 0 ,
sin 0
2
x
x x k k
x
sin sin cos cos
22
1 tan tan sin cot 4 sin cot 4
2
cos cos
2
xx
xx
x
x x x x x
x
x
+

+ + = + =


cos
2
sin cot 4
cos cos
2
x
xx
x
x
+ =
tan cot 4xx + =
2
tan 4tan 1 0xx − + =
tan 2 3
1
tan 2 3
23
x
x
=+
= − =
+
5
12
12
xk
xl
=+
=+
.
Với hai h nghiệm trên dễ thấy nghiệm dương nhỏ nhất là
12
; để đưc nghiệm âm lớn nhất ta
đều cho
1kl= = −
đưc nghiệm âm
7 11
;
12 12

−−
khi đ nghiệm âm lớn nhất là
7
12
−
.
Ta có
7
12 12 2
−
+ = −
.
Câu 40: Với
0; 1aa
, giá tr của biểu thc
log 5
a
a
là
A.
5
. B.
5
. C.
25
. D.
1
5
.
Lời giải
Tác giả: Cao Văn Tùng, FB: Cao Tung
Chọn C.
Ta có
( )
2
log 5
2log 5 log 5
2
5 25
a
aa
a a a= = = =
maihuongpla@gmail.com
Câu 41: Cho hình chóp
.S ABC
có
6SA =
,
5SB =
,
4SC =
,
00
45 , 60ASB BSC ASC= = =
. Tính thể
tích khối chóp
.S ABC
.
A.
16V =
. B.
10V =
. C.
14V =
. D.
12V =
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 28 Mã đề 388
Lời giải
Tác giả: Đặng Mai Hương. FB: maihuongpla
Chọn B.
Lấy
,M SA N SB
sao cho
4SM SN==
Áp dụng đnh lý cosin cho tam giác
SMN
2 2 2
2 . .cos 32 16 2 4 2 2MN SM SN SM SN MSN MN= + − = − = −
Tương tự
4 2 2CN =−
Gi
E
l trung điểm của
CM
, tam giác
NCM
cân tại
N
nên
NE CM⊥
ta có
22
2 7 4 2NE NC CE= − = −
suy ra
1
. 4 7 4 2
2
NCM
S MC NE= = −
Gi
R
l bn kính đường tròn ngoại tiếp tam giác
NCM
ta có:
( )
4 2 2
..
4.
7 4 2
NCM
NC NM CM
RR
S
−
= =
−
Vì
4SC SM SN= = =
suy ra hình chiếu của
S
trên mp
()NCM
trùng với tâm
O
đường tròn
ngoại tiếp tam giác
NCM
2 2 2 2
4
7 4 2
h SO SN ON SN R= = − = − =
−
.
1 16
.
33
S NMC NCM
V SO S==
. Ta có
.
..
.
8 15
. 10
15 8
S NMC
S ABC S NMC
S ABC
V
SM SN
VV
V SA SB
= = = =
Cách 2 : ( Dùng cho trắc nghiệm)
Đặt
6SA a==
,
5SB b==
,
4SC c==
,
0 0 0
45 ; 60 ; 45BSC x ASC y ASB z= = = = = =
.
Ta có thể tích khối chóp
.S ABC
là :
A
B
C
S
O
M
N
E
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 29 Mã đề 388
2 2 2
. 1 2cos .cos . os cos cos os
6
abc
V x y c z x y c z= + − − −
0 0 0 2 0 2 0 2 0
6.5.4
. 1 2cos45 .cos60 . os45 cos 45 cos 60 os 45 10
6
cc= + − − − =
Câu 42: Bất phương trình
2
2 3 0xx− + +
có tập nghiệm là
A.
( ) ( )
; 1 3;− − +
. B.
( )
1;3−
. C.
1;3−
. D.
( )
3;1−
.
Lời giải
Tác giả: Đặng Mai Hương. FB: maihuongpla
Chọn B.
Ta có:
2
2 3 0 1 3x x x− + + −
Ducchinh2308@gmail.com
Câu 43: Khẳng đnh no sau đây l đúng?
A.
a b a c b c + +
. B.
22
a b a b
.
C.
a b ac bc
. D.
ab
ab
cc
.
Lời giải
Tác giả: Huỳnh Đức Chính, FB: Huỳnh Đức Chính
Chọn A.
Theo tính chất của bất đẳng thc (cộng hai vế của một bất đẳng thc với cùng một biểu thc).
Giải thích thêm :
- Khẳng đnh B sai. Ví dụ:
2; 1ab= − =
. Ta có
21−
nhưng
( )
2
2
21−
.
- Khẳng đnh C sai. Ví dụ:
2; 3; 1a b c= = = −
. Ta có
23
nhưng
( ) ( )
2. 1 3. 1− −
.
- Khẳng đnh D sai. Ví dụ:
2; 3; 1a b c= = = −
. Ta có
23
nhưng
23
11
−−
.
Câu 44: Tính diện tích xung quanh của một hình nn c bn kính đy bằng
4cm
và chiều cao bằng
3cm
A.
2
20
xq
S cm
=
. B.
2
18
xq
S cm
=
. C.
2
15
xq
S cm
=
. D.
2
12
xq
S cm
=
.
Lời giải
Tác giả: Huỳnh Đức Chính, FB: Huỳnh Đức Chính
Chọn D.
Đường sinh của hình nón:
22
5l r h cm= + =
.
Diện tích xung quanh của hình nón:
2
20
xq
S rl cm

==
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 30 Mã đề 388
vuhangltt@gmail.com
Câu 45: Khối bát diện đều có bao nhiêu cạnh?
A.
1
. B.
8
.. C.
20
. D.
12
.
Lời giải
Tác giả: Vũ Thị Hằng, FB: Đạt Lâm Huy
Khối bát diện đều có
12
cạnh
Chọn D.
Câu 46: Mô đun của số phc
34zi=+
là
A.
4
. B.
7
. C.
3
. D.
5
Lời giải
Tác giả: Vũ Thị Hằng, FB: Đạt Lâm Huy
Chọn D.
22
3 4 5.z = + =
hientam112@gmail.com
Câu 47: Có bao nhiêu số tự nhiên có hai ch số mà cả hai ch số đ đều lẻ?
A.
20.
B.
50.
C.
25.
D.
45.
Lời giải
Họ và tên: Bùi Thị Thu Hiền- Fb Hiền Tấm
Chọn C.
- Gi số tự nhiên c hai ch số cần lập thỏa mãn yêu cầu bi ton l
ab
(
, 1;3;5;7;9ab
)
+ a: c 5 cch chn
+ b: có 5 cch chn.
D đ c: 5 x 5 = 25 cch lập số c 2 ch số m cả hai ch số đều lẻ. Chn C.
Câu 48: Cho hàm số
( )
fx
c đạo hàm trên v c đồ th của hàm
( )
y f x
=
đưc cho như hình vẽ.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 31 Mã đề 388
Biết rằng
( ) ( ) ( ) ( )
3 0 4 1f f f f− + = + −
. Giá tr lớn nhất và giá tr nhỏ nhất của
( )
fx
trên
đoạn
3;4−
lần lưt là:
A.
(4)f
và
( 3)f −
. B.
( 3)f −
và
(0)f
. C.
(4)f
và
(0)f
. D.
(2)f
và
( 3)f −
.
Họ và tên: Bùi Thị Thu Hiền- Fb Hiền Tấm
Lời giải
Chọn B.
Dựa vo đồ th của hm số
( )
y f x
=
ta c bảng biến thiên của hm số
( )
y f x=
:
x
−
-3
0
4
+
( )
fx
−
−
0
+
0
−
( )
fx
( )
3f −
( )
0f
( )
4f
( ) ( )
0 4 0ff

==
nên
0x =
và
4x =
l hai điểm cực tr của
( )
y f x=
.
Từ bảng biến thiên ta c
3;4
min ( ) (0)f x f
−
=
, đồng thời
( ) ( )
10ff−
. Do đ:
( ) ( ) ( ) ( )
3 0 4 1f f f f− + = + −
( ) ( ) ( ) ( ) ( ) ( )
3 4 1 0 0 3 4f f f f f f− − = − − −
.
3;4
max ( ) ( 3)f x f
−
= −
. Chn B
nguyentuanblog1010@gmail.com
Câu 49: Tìm tất cả các giá tr của tham số
m
để phương trình
2
2 1 0x x m− + − =
có hai nghiệm trái
dấu.
A.
2m
. B.
1m
. C.
1m
. D.
2m
.
Lời giải
Tác giả: Phạm Chí Tuân, FB: Tuân Chí Phạm
Chọn B.
Xét phương trình
2
2 1 0x x m− + − =
( )
1
.
Phương trình
( )
1
có hai nghiệm trái dấu khi và chỉ khi:
( )
0 1. 1 0 1ac m m −
.
Câu 50: Trong mặt phẳng với hệ ta độ
Oxy
, cho đường tròn
( ) ( )
2
2
: 2 36C x y+ + =
. Khi đ phép v tự
tỉ số
3k =
biến đường tròn
( )
C
thnh đường tròn
( )
'C
có bán kính là:
A.
108
. B.
12
. C.
6
. D.
18
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 32 Mã đề 388
Lời giải
Tác giả: Phạm Chí Tuân, FB: Tuân Chí Phạm
Chọn D.
Theo tính chất của phép v tự thì phép v tự tỉ số
k
biến đường tròn có bán kính
R
thành
đường tròn có bán kính
kR
.
Áp dụng vào bài toán ta có phép v tự tỉ số
3k =
biến đường tròn
( )
C
có bán kính
6R =
thành
đường tròn
( )
'C
có bán kính
' . 3 .6 18R k R= = =
.
Câu 51: Bất phương trình
( )
10xx−
có bao nhiêu nghiệm nguyên thuộc
1;2018−
?
A. 1. B. 2. C. 2019. D. 2018.
Lời giải
Tác giả: Nguyễn Văn Mộng, FB: Nguyễn Văn Mộng
Chọn C.
Ta có:
( )
0
0
10
0
10
1
0
0
10
x
x
x
x
xx
x
x
x
x

−
=
−
−
Xét nghiệm nguyên của bất phương trình đã cho trên
1;2018−
thì
0;1;2;...;2018x
Do đ, số nghiệm nguyên của bất phương trình đã cho l:
2018 0 1 2019− + =
. Vậy ta chn
C.
Câu 52: Cho hình chóp
.S ABCD
c đy
ABCD
là hình bình hành tâm
O
. Gi
M
l trung điểm của
OB
,
( )
là mặt phẳng đi qua
M
, song song với
AC
và song song với
SB
. Thiết diện của
hình chóp
.S ABCD
khi cắt bởi mặt phẳng
( )
là hình gì?
A. Lục giác. B. Ngũ gic. C. Tam giác. D. T giác.
Lời giải
Tác giả: Nguyễn Văn Mộng, FB: Nguyễn Văn Mộng
Chọn B.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 33 Mã đề 388
Ta có:
( ) ( )
( ) ( )
( ) ( )
1
//
M ABCD
ABCD d
ABCD AC

=
đi qua
M
và song song với
AC
.
Trong
( )
ABCD
, gi
,IH
lần lưt l giao điểm của
1
d
với
AB
và
BC
. Khi đ,
I
và
H
lần
lưt l trung điểm của
AB
và
BC
.
Ta lại có:
( ) ( )
( ) ( )
( ) ( )
2
//
I SAB
AB d
SAB SB

=
đi qua
I
và song song với
SB
.
Trong
( )
SAB
, gi
J
l giao điểm của
2
d
với
SA
. Khi đ,
J
l trung điểm của
SA
.
Ta cũng c:
( ) ( )
( ) ( )
( ) ( )
3
//
H SBC
SBC d
SBC SB

=
đi qua
H
và song song với
SB
.
Trong
( )
SBC
, gi
L
l giao điểm của
3
d
với
SC
. Khi đ,
L
l trung điểm của
SC
.
Mặt khác:
( ) ( )
( ) ( )
( ) ( )
4
//
M SBD
SBD d
SBD SB

=
đi qua
M
và song song với
SB
.
Trong
( )
SBC
, gi
K
l giao điểm của
4
d
với
SD
.
Vậy thiết diện của hình chóp
.S ABCD
khi cắt bởi mặt phẳng
( )
l ngũ gic
HIJKL
.
nhungcvp95@gmail.com
Câu 53: Trong không gian với hệ ta độ
Oxyz
, cho hai vectơ
( )
2;1; 2a =−
v vectơ
( )
1;0;2b =
.
Tìm ta độ vectơ
c
l tích c hướng của
a
và
b
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 34 Mã đề 388
A.
( )
2;6; 1c =−
. B.
( )
4;6; 1c =−
. C.
( )
4; 6; 1c = − −
. D.
( )
2; 6; 1c = − −
.
Lời giải
Tác giả: Phùng Nhung, FB: Phùng Nhung
Chọn D.
Áp dụng công thc tính tích c hướng trong hệ trục ta độ
Oxyz
ta đưc:
( )
, 2; 6; 1c a b

= = − −

Vậy chn đp n D.
nhungcvp95@gmail.com
Câu 54: Phương trình
32xx−=
có bao nhiêu nghiệm nguyên?
A. 3. B. 0. C. 2. D. 1.
Lời giải
Tác giả: Phùng Nhung, FB: Phùng Nhung
Chọn D.
Ta có:
2
32
1
3
32
1
2
23
2
3
x x x
x
xx
x
x x x

− =
=


− =
=

− =


Vậy số nghiệm nguyên của phương trình l 1.
xuanmda@gmail.com
Câu 55: Nghiệm của phương trình
3
24
x−
=
thuộc tập no dưới đây?
A.
5;8
. B.
(
;0−
. C.
( )
0;5
. D.
( )
8;+
.
Lời giải
Chọn A.
3 3 2
2 4 2 2 3 2 5 5;8
xx
xx
−−
= = − = =
Câu 56:
n
u
đưc cho bởi công thc no dưới đây l số hạng tổng quát của một cấp số nhân?
A.
1
1
2
n
n
u
+
=
. B.
2
1
2
n
un=−
. C.
1
1
2
n
n
u =−
. D.
2
1
2
n
un=+
.
Lời giải
Chọn A.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 35 Mã đề 388
1
1
1 1 1
.
2 4 2
n
n
n
u
−
+

==


là số hạng tổng quát của một cấp số nhân có
1
1
4
u =
và
1
2
q =
.
2
1
2
n
un=−
có
1 2 3
1 7 1 17 7
; .7; .7
2 2 2 2 2
u u u= = = =
nên không phải số hạng tổng quát của một
cấp số nhân.
1
1
2
n
n
u =−
có
1 2 3
1 3 1 3 7 3 3
; . ; .
2 4 2 2 8 4 2
u u u= − = − = − = − −
nên không phải số hạng tổng quát
của một cấp số nhân.
2
1
2
n
un=+
có
1 2 3
3 9 3 19 9
; .3; .3
2 2 2 2 2
u u u= = = =
nên không phải số hạng tổng quát của một
cấp số nhân.
diephd02@gmail.com
Câu 57: Cho tích phân
1
0
( 2) x
x
x e d a be− = +
, với
;ab
. Tổng
+ab
bằng
A.
1
. B.
−3
. C.
5
. D.
1−
.
Lời giải
Họ và tên: Nguyễn Ngọc Dip, FB: Nguyễn Ngọc Dip
Chọn A.
Đặt

= − =

− = − − − + − = − +

==



11
11
00
00
2x
( 2) x ( 2) x= 2 3 2e =
x
x x x x
xx
u x du d
x e d x e e d e e a be
dv e d v e
với
= = − + =; 3, 2 1a b a b a b
Câu 58: Có bao nhiêu tiếp tuyến với đồ th hàm số
1
1
x
y
x
+
=
−
, biết tiếp tuyến đ song song với đường
thẳng
2x 7y = − +
?
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Họ và tên: Nguyễn Ngọc Dip, FB: Nguyễn Ngọc Dip
Chọn C.
2
12
1 ( 1)
x
yy
xx
+−
= =
−−
.
Phương trình tiếp tuyến tại điểm
0 0 0
( ; )M x y
của đồ th hàm số
1
1
x
y
x
+
=
−
có dạng:
0
0 ( ) 0
()
x
y y y x x
− = −
. Do tiếp tuyến song song với đường thẳng
2x 7y = − +
nên
0
()
2
x
y
=−
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 36 Mã đề 388
00
2
00
2
00
0
x 0 1
2
2 2x 0
x 2 3
( 1)
y
x
y
x
= = −
−
= − − =
= =
−
Với
0
0 0 ( )
x 0, 1, 2
x
yy
= = − = −
. Phương trình tiếp tuyến cần lập:
21yx= − −
(nhận).
Với
0
0 0 ( )
x 2, 3, 2
x
yy
= = = −
. Phương trình tiếp tuyến cần lập:
27yx= − +
(loại).
Vậy có
1
tiếp tuyến của đồ th hàm số
1
1
x
y
x
+
=
−
song song với đường thẳng
2x 7y = − +
.
Slowrock321@gmail.com
Câu 59: Hàm số no dưới đây l hm số lẻ?
A. . B. . C. . D. .
Lời giải
Tác giả: Đỗ Minh Đăng, FB: Johnson Do
Chọn A.
Xét hàm số
+ TXĐ:
Ta có .
+ với
xD
Vậy hàm số là hàm số lẻ.
Câu 60: Trong không gian với hệ ta độ Oxyz, phương trình mặt phẳng trung trực của đoạn AB với
A. . B. . C. . D. .
Lời giải
Chọn A.
Gi I l trung điểm AB ,
Mặt phẳng trung trực (P) của đoạn AB qua I và vuông góc AB nên có VTPT .
Phương trình .
diephd02@gmail.com
Câu 61: Cho tích phân
1
0
( 2) x
x
x e d a be− = +
, với
;ab
. Tổng
+ab
bằng
A.
1
. B.
−3
. C.
5
. D.
1−
.
Lời giải
44y x x= − − +
33y x x= − + +
yx=
2
51y x x= − +
( )
44y f x x x= = − − +
D =
x D x D −
( )
( )
( )
4 4 4 4f x x x x x f x− = − − − − + = − − − + = −
( )
44y f x x x= = − − +
( ) ( )
1, 3,2 , 1,5,4AB−−
4 7 0x y z− − + =
4 7 0x y z− − − =
4 18 0x y z− − − =
4 18 0x y z− − + =
( )
0,1,3I
( ) ( )
2,8,2 2 1, 4, 1AB = − = − − −
( )
1, 4, 1n = − −
( ) ( )
( ): 4 1 3 0 4 7 0P x y z x y z− − − − = − − + =
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 37 Mã đề 388
Họ và tên: Nguyễn Ngọc Dip, FB: Nguyễn Ngọc Dip
Chọn A
Đặt

= − =

− = − − − + − = − +

==



11
11
00
00
2x
( 2) x ( 2) x= 2 3 2e =
x
x x x x
xx
u x du d
x e d x e e d e e a be
dv e d v e
với
= = − + =; 3, 2 1a b a b a b
Câu 62: Có bao nhiêu tiếp tuyến với đồ th hàm số
1
1
x
y
x
+
=
−
, biết tiếp tuyến đ song song với đường
thẳng
2x 7y = − +
?
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Họ và tên: Nguyễn Ngọc Dip, FB: Nguyễn Ngọc Dip
Chọn C.
2
12
1 ( 1)
x
yy
xx
+−
= =
−−
.
Phương trình tiếp tuyến tại điểm
0 0 0
( ; )M x y
của đồ th hàm số
1
1
x
y
x
+
=
−
có dạng:
0
0 ( ) 0
()
x
y y y x x
− = −
. Do tiếp tuyến song song với đường thẳng
2x 7y = − +
nên
0
()
2
x
y
=−
00
2
00
2
00
0
x 0 1
2
2 2x 0
x 2 3
( 1)
y
x
y
x
= = −
−
= − − =
= =
−
Với
0
0 0 ( )
x 0, 1, 2
x
yy
= = − = −
. Phương trình tiếp tuyến cần lập:
21yx= − −
(nhận).
Với
0
0 0 ( )
x 2, 3, 2
x
yy
= = = −
. Phương trình tiếp tuyến cần lập:
27yx= − +
(loại).
Vậy có
1
tiếp tuyến của đồ th hàm số
1
1
x
y
x
+
=
−
song song với đường thẳng
2x 7y = − +
.
Slowrock321@gmail.com
Câu 63: Hàm số no dưới đây l hm số lẻ?
A. . B. . C. . D. .
Lời giải
Tác giả: Đỗ Minh Đăng, FB: Johnson Do
Chọn A
Xét hàm số
44y x x= − − +
33y x x= − + +
yx=
2
51y x x= − +
( )
44y f x x x= = − − +
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 38 Mã đề 388
+ TXĐ:
Ta có .
+ với
xD
Vậy hàm số là hàm số lẻ.
Câu 64: Trong không gian với hệ ta độ Oxyz, phương trình mặt phẳng trung trực của đoạn AB với
A. . B. . C. . D. .
Lời giải
Chọn A
Gi I l trung điểm AB ,
Mặt phẳng trung trực (P) của đoạn AB qua I và vuông góc AB nên có VTPT .
Phương trình .
Mar.nang@gmail.com
Câu 65: Tính tổng
1 2 3 2018
2018 2018 2018 2018
...S C C C C= + + + +
bằng.
A.
2018
2
. B.
2018
21−
. C.
2018
21+
. D.
2019
21−
.
Lời giải
Tác giả: Lê Đình Năng, FB: Lê Năng
Chọn B
Xét khai triển nh thc Niu-tơn:
( )
2018
0 1 2 2 2018 2018
2018 2018 2018 2018 2018
1 ... ...
kk
x C C x C x C x C x+ = + + + + + +
(*).
Thay
1x =
vào hai vế của (*) ta đưc:
2018 1 2 2018 1 2 2018 2018
2018 2018 2018 2018 2018 2018
2 1 ... ... 2 1C C C S C C C= + + + + = + + + = −
.
Vậy
2018
21S =−
.
Câu 66: Cho tam giác
ABC
có chu vi bằng 12 vbn kính đường tròn nội tiếp bằng 1. Diện tích của
tam giác
ABC
bằng
A.
12
. B.
3
. C.
6
. D.
24
.
Lời giải
Tác giả: Lê Đình Năng, FB: Lê Năng
Chọn C
D =
x D x D −
( )
( )
( )
4 4 4 4f x x x x x f x− = − − − − + = − − − + = −
( )
44y f x x x= = − − +
( ) ( )
1, 3,2 , 1,5,4AB−−
4 7 0x y z− − + =
4 7 0x y z− − − =
4 18 0x y z− − − =
4 18 0x y z− − + =
( )
0,1,3I
( ) ( )
2,8,2 2 1, 4, 1AB = − = − − −
( )
1, 4, 1n = − −
( ) ( )
( ): 4 1 3 0 4 7 0P x y z x y z− − − − = − − + =
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 39 Mã đề 388
Theo đề bài tam giác
ABC
có chu vi bằng 12 nên nửa chu vi là
12
2
p =
; bn kính đường tròn
nội tiếp bằng 1, tc là ta có:
1r =
.
Diện tích tam giác
ABC
là:
. 6.1 6S p r= = =
.
Maisonltt@gmail.com
Câu 67: Tính tích phân
2
0
(2 1)I x dx=+
A.
5I =
. B.
6I =
. C.
2I =
. D.
4I =
.
Lời giải
Tác giả: Nguyễn Thi Mai, FB: Mai Nguyễn
Chọn B
Ta có
( )
2
2
2
0
0
(2 1) 4 2 6I x dx x x= + = + = + =
.
Maisonltt@gmail.com
Câu 68: Tính diện tích hình phẳng giới hạn bởi đồ th hàm số
2
4y x x=−
và trục
Ox
A.
11
. B.
34
3
. C.
31
3
. D.
32
3
.
Lời giải
Tác giả:Nguyễn Thị Mai, FB: Mai Nguyễn
Chọn D
Gi
S
là diện tích hình phẳng giới hạn bởi đồ th hàm số
2
4y x x=−
và trục
Ox
.
Xét phương trình
2
0
40
4
x
xx
x
=
− =
=
.
Ta có
4
44
3
2 2 2
00
0
32
4 (4 ) (2 )
33
x
S x x dx x x dx x= − = − = − =

.
tanbaobg@gmail.com
Câu 69: Cho các số phc
z
thỏa mãn
25z =
. Biết rằng trong mặt phẳng ta độ cc điểm biểu diễn
của số phc
( )
2w i i z= + −
cùng thuộc một đường tròn cố đnh. Tính bán kính
r
của đường
tròn đ?
A.
5r =
. B.
10r =
. C.
20r =
. D.
25r =
.
Lời giải
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 40 Mã đề 388
Tác giả:Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo
Chọn B
Ta có
( ) ( )
22w i i z w i i z= + − − = −
. Suy ra
( )
2 2 . 10w i i z i z− = − = − =
.
Vậy tập hp điểm biểu diễn của số phc
w
trên mặt phẳng ta độ nằm trên đường tròn có bán
kính
10r =
.
Câu 70: Phủ đnh của mệnh đề “
2
:0xx
” l mệnh đề no sau đây?
A.
2
:0xx
. B.
2
:0xx
. C.
2
:0xx
. D.
2
:0xx
.
Lời giải
Tác giả: Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo
Chọn D
Ta sử dụng kết quả:
Mệnh đề phủ đnh của mệnh đề “
( )
:x D P x
” l mệnh đề “
( )
:x P x
”.
hakhanhhuyen229@gmail.com
Câu 71: Trong mặt phẳng với hệ ta độ
Oxy
, nếu phép tnh tiến theo vectơ
v
biến điểm
(1;2)A
thành
điểm
(1; 6)B −
thì nó biến đường thẳng
:2 3 0d x y− + =
thnh đường thẳng
'd
c phương trình
A.
2 3 0xy− − =
. B.
20xy−=
. C.
2 8 0xy− − =
. D.
2 5 0xy− − =
.
Lời giải
Tác giả:Hà Khánh Huyền, FB: Hà Khánh Huyền
Chọn D
( ) (0; 8)
v
T A B AB v v= = − =
hay
(0; 8)v =−
.
Biểu thc ta độ của phép tnh tiến
'
.
'8
v
xx
T
yy
=
=−
Lấy điểm
( ; )M x y d
thì
2 3 0 (*)xy− + =
.
Gi
( ) '( '; ')
v
T M M x y=
. Lại có
( ) '
v
T d d=
nên
''Md
.
Từ
''
.
' 8 ' 8
x x x x
y y y y
==


= − = +

Thay vào
(*)
ta có:
2 ' ( ' 8) 3 0 2 ' ' 5 0.x y x y− + + = − − =
Vậy phương trình của đường thẳng
'd
là
2 5 0xy− − =
.
Câu 72: Cho hàm số
()y f x=
có tập xc đnh là
\1
và liên tục trên mỗi khoảng xc đnh của nó.
Biết
()fx
có bảng biến thiên như sau
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 41 Mã đề 388
Số nghiệm của phương trình
( ) 6fx=
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Tác giả: Hà Khánh Huyền, FB: Hà Khánh Huyền
Chọn C
Dựa vào bảng biến thiên
2
( ) 6
( 1)
x
fx
x a a
=
=
=
Vậy phương trình
( ) 6fx=
có 2 nghiệm.
maisonltt@gmail.com
Câu 73: Xét trong không gian, mệnh đề no dưới đây l đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với
đường thẳng còn lại.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng th ba thì song song với
nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng th ba thì vuông góc với
nhau.
Lời giải
Họ và tên tác giả: Nguyễn Thị Mai. Tên FB: Mai Nguyễn
Chọn B
maisonltt@gmail.com
Câu 74: Phép quay góc
0
90
biến đường thẳng
d
thnh đường thẳng
'd
. Khi đ
A.
'd
song song với
d
. B.
'd
trùng
d
.
C.
'd
tạo với
d
góc
0
60
D.
'd
vuông góc với
d
.
Lời giải
Họ và tên tác giả: Nguyễn Thị Mai. Tên FB: Mai Nguyễn
Chọn D
bichngock36@gmail.com
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 42 Mã đề 388
Câu 75: Trong mặt phẳng ta độ điểm biểu diễn số phc
z
thỏa mãn
1 2 3zi− − =
là
A. đường tròn tâm
(1;2)I
, bán kính
9R =
. B. đường tròn tâm
(1;2)I
, bán kính
3R =
.
C. đường tròn tâm
( 1; 2)I −−
, bán kính
3R =
. D.
đường thẳng c phương trình
2 3 0xy+ − =
.
Lời giải
Tác giả: Nguyễn Mạnh Dũng, FB: dungmanhnguyen
Chọn C
Giả sử điểm
M(x;y)
l điểm biểu diễn số phc
z
. Ta có:
22
1 2 3 ( 1) ( 2)i 3 ( 1) ( 2) 9z i x y x y− − = − + − = − + − =
Vậy điểm
M(x;y)
thuộc đường tròn
22
( 1) ( 2) 9xy− + − =
có tâm
(1;2)I
, bán kính
3R =
.
Câu 76: Trong khai triển của biểu thc
8
2
1
2.x
x

−


Hệ số của
7
x
là:
A.
112
. B.
112−
. C.
1792−
. D.
1792
.
Lời giải
Tác giả: Nguyễn Mạnh Dũng, FB: dungmanhnguyen
Chọn C
Ta có:
8
2 2 8 8 16 2 8 16 3
8 8 8
11
2 . .( 2 ) .( 2) . . .( 2) .
k
k k k k k k k k k
x C x C x x C x
xx
− − − − − −
− = − = − = −
Yêu cầu bài toán
16 3 7 3kk − = =
Với
3k =
thì hệ số của
7
x
là:
3 8 3
8
.( 2) 1792C
−
− = −
tcdung.math@gmail.com
Câu 77: Để lấy nước tưới cây, ông Tráng cần xây một bể cha nước có dạng hình hộp ch nhật không
có nắp đậy. Nếu bể cần có thể tích
3
50m
và chiều dài gấp 4 lần chiều rộng thì chiều cao bằng
bao nhiêu để chi phí vật liệu thấp nhất.
A.
4,5m
. B. 5m.
C.
2,5m
. D.
2m
Lời giải
Tác giả: Trần Công Dũng, FB: trancong.dung.948
Chọn C
Gi chiều rộng của bể là
( )
,0x m x
. Khi đ chiều dài
4 ( )xm
và chiều cao
2
50 25
( ).
42
m
xx
=
Diện tích các mặt cần xây:
( ) ( )
( )
2 2 2
2
25 250
4 2 4 . 4 .
22
S x x x x x m
xx
= + + = +
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 43 Mã đề 388
( )
/3
2
250 125 5
8 0 .
2 8 2
S x x x x
x
= − = = =
Chi phí thấp nhất khi
( )
Sx
đạt giá tr nhỏ nhất trên
( )
0;+
. Do đ
( )
2,5xm=
.
tcdung.math@gmail.com
Câu 78: Trong mặt phẳng với hệ ta độ
Oxy
cho đường thẳng
:2 3 4 0d x y− + =
. Vectơ no sau đây l
một vectơ chỉ phương của d.
A.
( )
4
3; 2u =−
. B.
( )
2
2;3u =
.
C.
( )
1
2; 3u =−
. D.
( )
3
3;2u =
Lời giải
Tác giả: Trần Công Dũng, FB: trancong.dung.948
Chọn D
Ta thấy đường thẳng
d
có một vectơ php tuyến là
( )
2; 3−
. Do đ
( )
3
3;2u =
là một vectơ chỉ
phương của d.
Leminh0310@gmail.com
Câu 79: Cho
tan 2a =
. Tính giá tr biểu thc
2sin cos
sin cos
aa
P
aa
−
=
+
.
A.
2P =
. B.
1P =
. C.
5
3
P =
. D.
1P =−
.
Tác giả: Lê Hồ Quang Minh, FB: Lê Minh
Lời giải
Chọn B
Ta có:
2sin cos 2tan 1 2.2 1
1
sin cos tan 1 2 1
a a a
P
a a a
− − −
= = = =
+ + +
.
Câu 80: Khẳng đnh no sau đây l sai?
A.
( )
sin sin

− = −
. B.
( )
cot cot

− = −
. C.
( )
cos cos

− = −
. D.
( )
tan tan

− = −
.
Tác giả: Lê Hồ Quang Minh, FB: Lê Minh
Lời giải
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 44 Mã đề 388
Chọn C
Dễ thấy C sai vì
( )
cos cos

−=
.
Email: ngonguyenanhvu@gmail.com
Câu 81: Trong mặt phẳng với hệ ta độ
Oxy
, cho đường thẳng
: 4 15 0d x y− + =
v điểm
( )
2; 0A
.
Tìm ta độ điểm
M
thuộc
d
để đoạn
AM
c độ dài nhỏ nhất.
A.
( )
15; 0M −
. B.
( )
5; 5M
. C.
( )
0; 3M
. D.
( )
1; 4M
.
Lời giải
Tác giả: Ngô Nguyễn Anh Vũ, FB: Euro Vu
Chọn D
Điểm
( )
4 15;M d M t t −
Ta có:
( )
( )
( )
22
22
4 17 17 8 17 17 4 1 17AM t t t t t

= − + = − + = − +


,
t
.
=min AM
17
, đạt đưc tại
4t =
. Khi đ
( )
1; 4M
.
Câu 82: Thể tích khối lăng trụ tam gic đều có tất cả các cạnh đều bằng
a
là
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
2
12
a
. D.
3
2
4
a
.
Lời giải
Tác giả: Ngô Nguyễn Anh Vũ, FB: Euro Vu
Chọn B
Hình lăng trụ tam gic đều l hình lăng trụ đng c đy l tam gic đều
23
' ' '
33
= '. .
44
ABC A B C ABC
aa
V AA S a
==
.
Thuylinh133c3@gmail.com
Câu 83: Cho t diện đều
ABCD
c độ di cạnh bằng
a
. Tính tích vô hướng của hai vectơ
AB
v
CD
.
A.
.0AB CD =
. B.
2
.AB CD a=
. C.
2
.
2
a
AB CD =
. D.
2
.AB CD a=−
.
Lời giải
Tác giả: Nguyễn Thùy Linh, FB: Nguyễn Thùy Linh
Chọn A
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề KT Năng Lực GV Bắc Giang 2018-2019
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 45 Mã đề 388
Gi
M
l trung điểm của
DC
.
Do
ABCD
l t diện đều nên ta c:
( )
DC AM
DC AMB DC AB
DC BM
⊥
⊥ ⊥
⊥
. 0.AB CD =
Thuylinh133c3@gmail.com
Câu 84: Một hộp đựng 9 quả cầu đưc đnh số lần lưt từ 1 đến 9. Lấy ngu nhiên một quả cầu từ hộp
đ. Tính xc suất lấy đưc quả cầu mang số chn.
A.
2
3
. B.
5
9
. C.
4
5
. D.
4
9
.
Lời giải
Tác giả: Nguyễn Thùy Linh, FB: Nguyễn Thùy Linh
Chọn D
Xét phép thử: “Lấy ngu nhiên một quả cầu từ hộp đựng 9 quả cầu”
Ta c:
( )
1
9
9.nC = =
Gi
A
là biến cố: “ Lấy đưc quả cầu mang số chn
"
( ) ( )
( )
( )
4
4.
9
nA
n A P A
n
= = =
| 1/45
| | Tải xuống

Có thể bạn quan tâm:

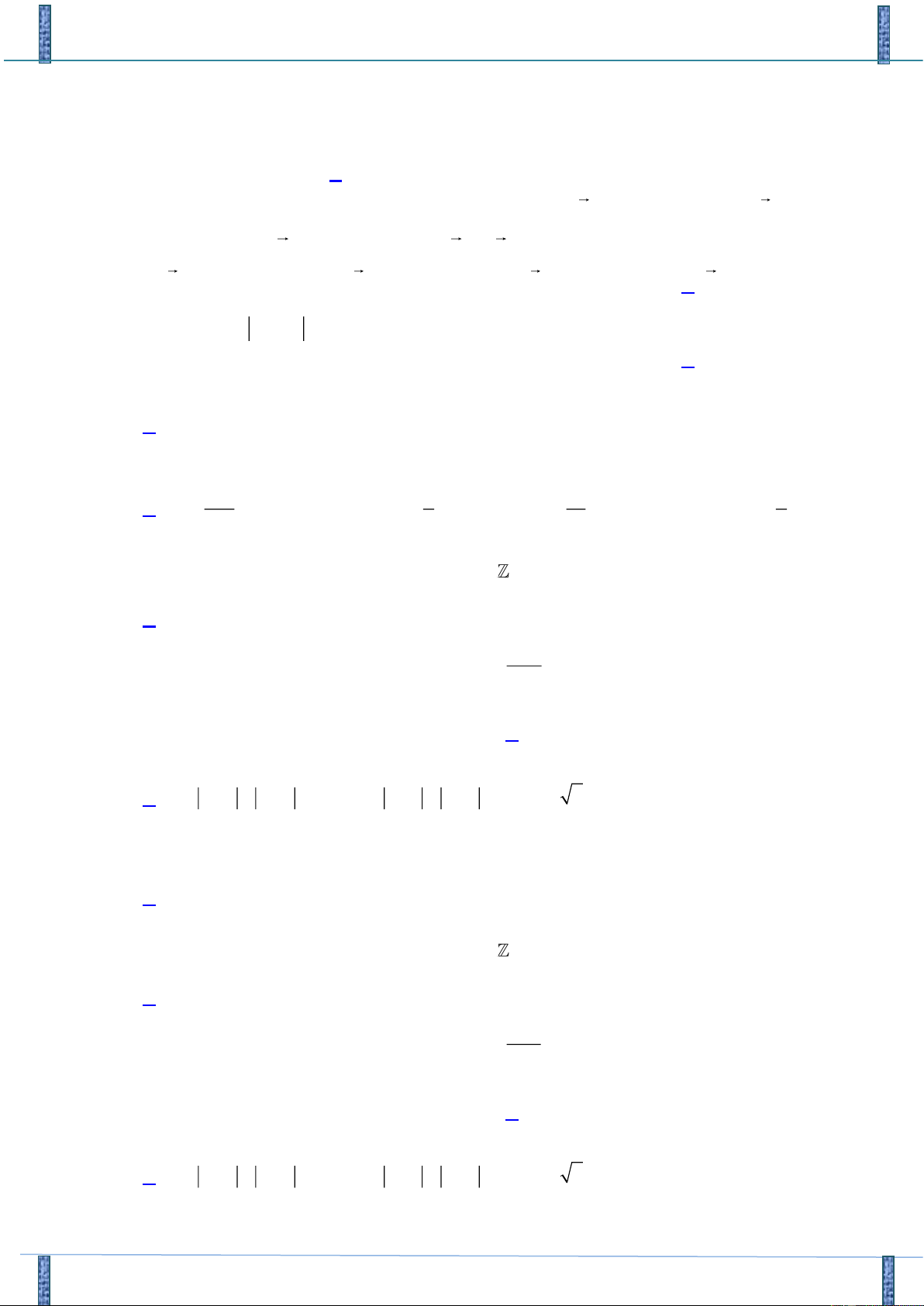
Preview text:

Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
SỞ GD&ĐT BẮC GIANG
ĐỀ THI TRẮC NGHIỆM
HỘI ĐỒNG KTKT GIÁO VIÊN MÔN TOÁN THPT NĂM HỌC 2018 - 2019
Thời gian làm bài: 90 phút (80 câu trắc nghiệm) ------------------ MÃ ĐỀ: 385
(Giáo viên không được sử dụng tài liệu)
Họ tên giáo viên: ............................................................................... Ngày sinh: ................. SBD: .................
Trường: ......................................................................................... .... Huyện / thành phố: ...............................
Tuonganh0209@gmail.com Câu 1:
Trong mặt phẳng với hệ trục Oxy , cho hai đường tròn (C ) ( x − )2 2 : 1 + y = 4 và
(C) (x − )2 +( y − )2 : 4 3
=16 cắt nhau tại hai điểm phân biệt A và B . Lập phương trình đường thẳng AB
A. x + y − 2 = 0 .
B. x − y + 2. = 0
C. x + y + 2 = 0 .
D. x − y − 2 = 0 . Câu 2:
Một hình trụ có diện tích xung quanh bằng 16 và thiết diện qua trục của hình trụ này là một
hình vuông. Thể tích V A. 32 2 . B. 18 . C. 16 . D. 24 . Câu 3:
Một cấp số cộng gồm 5 số hạng. Hiệu số hạng đầu và số hạng cuối bằng 20 . Tìm công sai d
của cấp số cộng đã cho A. d = 5 − . B. d = 4 . C. d = 4 − . D. d = 5. Câu 4:
Với hai véc tơ không cùng phương a và b . Xét hai véc tơ u = 2a − 3b và v = a + (x −1)b . Tìm
x để u và v cùng phương. 3 1 1 3 A. x = . B. x = . C. x = − . D. x = − . 2 2 2 2 Câu 5:
Giá trị lớn nhất của hàm số y = 2 sin x +1 là 1 A. −1. B. 1. C. − . D. 3 . 2 Câu 6:
Cho tứ diện ABCD. Gọi M , N lần lượt là trung điểm của BC , AD . Biết AB = 2a ,
CD = 2a 2 và MN = a 5. Số đo góc giữa hai đường thẳng AB và CD là A. 60 . B. 30 . C. 90 . D. 45 . Câu 7:
Điều kiện xác định của phương trình x − 2 = 8 − x là
A. x 2;8  . B. x  8 . C. x  2 . D. x  8 . Câu 8:
Mẹ hơn Minh 25 tuổi. Biết rằng 4 năm về trước tuổi của mẹ gấp 6 lần tuổi của Minh. Hãy
tính tuổi của Minh hiện nay. A. 9 tuổi. B. 5 tuổi. C. 8 tuổi. D. 10 tuổi.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 1 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 x x 2
log x − 3log x + 2 = 0 P = x + x Câu 9:
Gọi 1 , 2 là hai nghiệm của phương trình 2 2 . Tính 1 2 . A. 6 . B. 3 − . C. 2 . D. 3 . Câu 10: Cho hàm số 3 2
y = x − 3x − 2x −1 có đồ thị (C ) . Phương trình tiếp tuyến với (C ) tại giao điểm
của (C ) với trục tung là A. y = 2 − x −1.
B. y = 2x −1.
C. y = 2x +1. D. y = 2 − x +1.
Câu 11: Trong mặt phẳng với hệ trục tọa độ ( ;
O i, j ) , cho hai vectơ a = 2i − j và b = ( 4 − ;2) . Khẳng
định nào sau đây là đúng?
A. a và b cùng hướng.
B. a và b ngược hướng. C. a = ( 1 − ;2) . D. a = (2; ) 1 .
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA ⊥ ( ABCD) và
SA = a . Gọi M là trung điểm của cạnh SC . Khoảng cách từ M đến mặt phẳng (SBD) bằng: a a 4a 2a A. . B. . C. . D. . 2 3 3 3 Câu 13: Biết ( 2 lim
4x + ax +1 + bx = − . Tính giá của biểu thức 2 3
P = a − 2b . →− ) 1 x A. P = 32 . B. P = 0 . C. P = 16 . D. P = 8 .
Câu 14: Xếp 6 học sinh gồm 3 học sinh nam và 3 học sinh ngồi vào hai dãy ghế đối diện nhau, mỗi
dãy có 3 ghế (mỗi học sinh ngồi một ghế, các ghế đều khác nhau). Hỏi có bao nhiêu cách xếp
sao cho không có hai học sinh cùng giới ngồi đối diện nhau. A. 720. B. 36. C. 288. D. 72.
Câu 15: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy. Tính diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD 2 4 a 2 7 a A. 2 S = 3 a . B. S = . C. S = . D. 2 S = 7 a . 3 3
Câu 16: Tìm x để hai vectơ a = ( ;
x 2) và b = (2; 3
− ) có giá vuông góc với nhau. A. 3. B. 0. C. 3 − . D. 2. x y
Câu 17: Trong mặt phẳng với hệ tọa độ Oxy, cho elip ( E ) 2 2 : +
= 1. Tiêu cự của (E) bằng 25 9 A. 10. B. 16. C. 4. D. 8.
Câu 18: Cho hai tập hợp A = −1;3) và B = 1;5 . Giao của A và B là tập hợp nào sau đây? A. −1;5 . B. 1;3) . C. 1;  3 . D. 1;  2 .  
Câu 19: Biết các nghiệm của phương trình 1 cos 2x = − có dạng x =
+ k và x = − + k , k  ; 2 m n với ,
m n là các số nguyên dương. Khi đó m + n bằng A. 4. B. 3. C. 5. D. 6. 2 
Câu 20: Cho số phức z = 1− 2i . Tìm số phức =1+ z − z .
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 2 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 1 5 A.  = + i . B.  = 1 − − 6i .
C.  = 5 + 2i .
D.  = 3 − 2i . 2 2
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Giao tuyến của hai mặt
phẳng ( SAB) và ( SCD) là đường thẳng nào dưới đây?
A. Đường thẳng SO .
B. Đường thẳng AC .
C. Đường thẳng đi qua S và song song AB .
D. Đường thẳng đi qua S và song song với AD .
Câu 22: Hàm số nào dưới đây đồng biển trên ? 2x +1 A. 4 2
y = x + x . B. 3
y = x + 3x . C. y = . D. 3
y = −x − x . x + 3
Câu 23: Biết rằng với mọi giá trị thực của tham số m , các đường thẳng d : y = (m − 2)x + 2m − 3 cùng m
đi qua một điểm cố định là I (a; b) . Tính giá trị của biểu thức: S = a + b A. S = 3 − . B. S = 1 − . C. S = 1. D. S = 3.
Câu 24: Hàm số nào dưới đây đồng biến trên khoảng (0; + ) ? A. y = log x .
B. y = log x .
C. y = log x .
D. y = log x . 3  e 1 6 3 4
Câu 25: Trong không gian với hệ tọa độ Oxyz , cho
mặt cầu (S ) có phương trình 2 2 2
x + y + z + 4x − 2 y − 4 = 0 .Tính bán kính R của (S ). A. 1. B. 9 . C. 2 . D. 3 .
Câu 26: Điểm cực đại của hàm số 3 2
y = x − 3x + 2019 là A. y = 2019 .
B. M (0; 2019) . C. x = 0 . D. x = 2 .
Câu 27: Tập xác định của hàm số y = cot x là:   A.
\ k 2 , k   . B.
\  + k , k   .  2    C.
\ k , k   . D.
\  + k2 , k   .  2 
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : x + y − z −1 = 0 và đường thẳng x + 2 y − 4 z +1 d : = = 2 2 −
. Viết phương trình đường thẳng d là hình chiếu vuông góc của d trên 1 (P) . x + 2 y z +1 x − 2 y z −1 A. d : = = . B. d : = = . 7 5 − 2 7 5 − 2 x + 2 y z +1 x − 2 y z −1 C. d  : = = . D. d  : = = . 7 5 2 7 5 2
Câu 29: Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai điểm A(−3; 4) và B (5;6) . Trung điểm của
đoạn thẳng AB có tọa độ là A. (1;5) . B. (4; ) 1 . C. (5; ) 1 . D. (8; 2) .
Câu 30: Một nguyên hàm của hàm số f ( x) 2 = 3x là
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 3 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 A. ( ) 3
F x = x + x . B. F ( x) 3 = x +1.
C. F ( x) = 6x . D. F ( x) 3 = 3x .
Câu 31: Cho tam giác ABC . Khẳng định nào sau đây là sai?
A. AB − AC = CB .
B. AB + BA = 0 .
C. AB − AC = BC .
D. AB + BC = AC . x
Câu 32: Tập xác định của hàm số f ( x) = là 2 x −1
A. 0; +) \   1 . B. (1; +) . C. 0; ) 1 . D. \ −1;  1 .
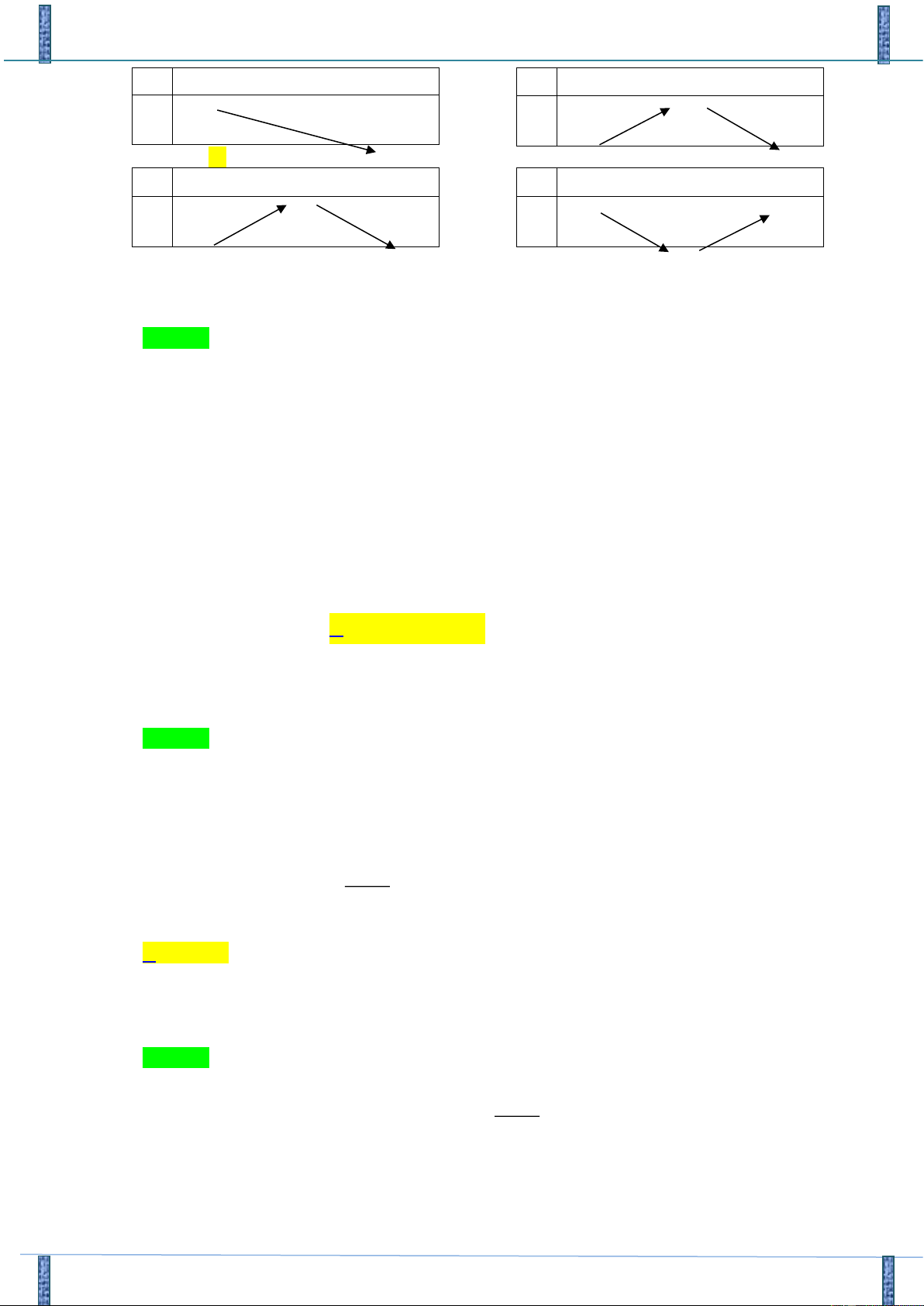
Câu 33: Bảng biến thiên nào dưới đây là của hàm số 2
y = −x + 2x + 2 ? A. B. x − + x − −1 + + − y y 1 − − − C. D. x − 1 + x − 1 + 3 + + y y − − 3
Câu 34: Đạo hàm của hàm số f ( x) 2 = sin x là:
A. f '( x) = 2sin x .
B. f '( x) = 2 cos x .
C. f '( x) = − sin (2x) . D. f '( x) = sin (2x) . 2  x − 4  khi x  2 −
Câu 35: Tìm m để hàm số f (x) =  x + 2
liên tục tại x = 2 −  m khi x = 2 − A. m = 4 − . B. m = 2 . C. m = 4 . D. m = 0 . x −
Câu 36: Tìm tất cả các giá trị của tham số m để đồ thị của hàm số 3 9 y = có tiệm cận đứng x + m A. m  3 − . B. m  3 . C. m = 3 . D. m = 3 − . 2019 2018 − + +
Câu 37: Tính lim( 2n 3n 4) ? A. − . B. + . C. 2 − . D. 2019 . u  = 2  1
Câu 38: Cho dãy số (U xác định bởi  Tính u ? n ) * 10 u
= u + 5, nNn 1+ n A. 57 . B. 62 . C. 47 . D. 52 .
Câu 39: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình  x  1+ tan x tan
sin x + cot x = 4   là  2      A. − . B. . C. . D. − . 6 2 6 2 log 5
Câu 40: Với a  0; a  1 , giá trị của biểu thức a a là 1 A. 5 . B. 5 . C. 25 . D. . 5
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 4 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Câu 41: Cho hình chóp S.ABC có SA = 6 , SB = 5 , SC = 4 , 0 0
ASB = BSC = 45 , ASC = 60 . Tính thể
tích khối chóp S.ABC . A. V = 16 . B. V = 10 . C. V = 14 . D. V = 12 .
Câu 42: Bất phương trình 2
−x + 2x + 3  0 có tập nghiệm là A. ( ; − − )
1  (3; +) . B. ( 1 − ;3) . C. −1;3 . D. (−3; ) 1 .
Câu 43: Khẳng định nào sau đây là đúng?
A. a b a + c b + c . B. 2 2
a b a b . a b
C. a b ac bc .
D. a b   . c c
Câu 44: Tính diện tích xung quanh của một hình nón có bán kính đáy bằng 4cm và chiều cao bằng 3cm A. 2 S = 20 cm . B. 2 S = 18 cm . C. 2 S = 15 cm . D. 2 S = 12 cm . xq xq xq xq
Câu 45: Khối bát diện đều có bao nhiêu cạnh? A. 1. B. 8 .. C. 20 . D. 12 .
Câu 46: Mô đun của số phức z = 3 + 4i là A. 4 . B. 7 . C. 3 . D. 5
Câu 47: Có bao nhiêu số tự nhiên có hai chữ số mà cả hai chữ số đó đều lẻ? A. 20. B. 50. C. 25. D. 45.
Câu 48: Cho hàm số f ( x) có đạo hàm trên
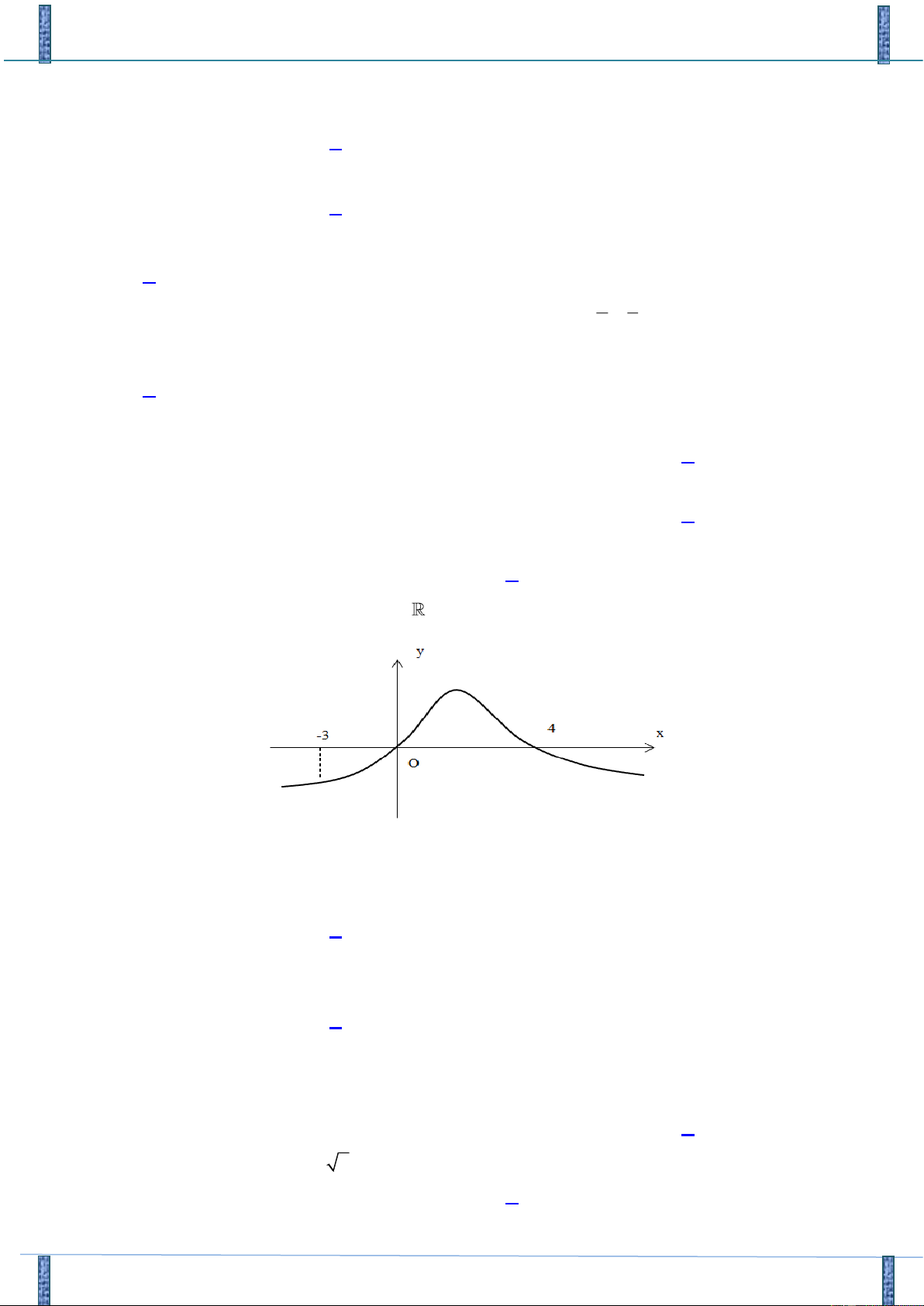
và có đồ thị của hàm y = f ( x) được cho như hình vẽ.
Biết rằng f (−3) + f (0) = f (4) + f (− )
1 . Giá trị lớn nhất và giá trị nhỏ nhất của f ( x) trên
đoạn −3;4 lần lượt là:
A. f (4) và f (−3) .
B. f (−3) và f (0) .
C. f (4) và f (0) .
D. f (2) và f (−3) .
Câu 49: Tìm tất cả các giá trị của tham số m để phương trình 2
x − 2x + m −1 = 0 có hai nghiệm trái dấu. A. m  2 . B. m  1. C. m  1. D. m  2 .
Câu 50: Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn (C ) x + ( y + )2 2 : 2
= 36 . Khi đó phép vị tự
tỉ số k = 3 biến đường tròn (C ) thành đường tròn (C ') có bán kính là: A. 108 . B. 12 . C. 6 . D. 18 .
Câu 51: Bất phương trình ( x − ) 1
x  0 có bao nhiêu nghiệm nguyên thuộc −1; 2018 ? A. 1. B. 2. C. 2019. D. 2018.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 5 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Câu 52: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của
OB , ( ) là mặt phẳng đi qua M , song song với AC và song song với SB . Thiết diện của
hình chóp S.ABCD khi cắt bởi mặt phẳng ( ) là hình gì? A. Lục giác. B. Ngũ giác. C. Tam giác. D. Tứ giác.
Câu 53: Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a = (2;1; 2
− ) và vectơ b = (1;0;2).
Tìm tọa độ vectơ c là tích có hướng của a và b .
A. c = (2;6;− ) 1 .
B. c = (4;6;− ) 1 . C. c = (4; 6 − ;− ) 1 . D. c = (2; 6 − ;− ) 1 .
Câu 54: Phương trình 3x − 2 = x có bao nhiêu nghiệm nguyên? A. 3. B. 0. C. 2. D. 1. −
Câu 55: Nghiệm của phương trình x 3 2
= 4 thuộc tập nào dưới đây? A. 5;8. B. ( ; − 0 . C. (0;5) . D. (8; +) .
Câu 56: u được cho bởi công thức nào dưới đây là số hạng tổng quát của một cấp số nhân? n 1 1 1 1 A. u = . B. 2 u = n − . C. u = −1. D. 2 u = n + . n n 1 2 + n 2 n 2n n 2 1
Câu 57: Cho tích phân ( − 2) x x
e dx = a + be  , với ;
a b . Tổng a + b bằng 0 A. 1. B. −3 . C. 5 . D. 1 − . x +1
Câu 58: Có bao nhiêu tiếp tuyến với đồ thị hàm số y =
, biết tiếp tuyến đó song song với đường x −1 thẳng y = 2 − x + 7 ? A. 2 . B. 0 . C. 1. D. 3 .
Câu 59: Hàm số nào dưới đây là hàm số lẻ? 2
A. y = x − 4 − x + 4 .
B. y = 3 − x + 3 + x . C. y = x .
D. y = x − 5x +1 .
Câu 60: Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng trung trực của đoạn AB với A(1, 3 − , 2), B( 1 − ,5, 4)
A. x − 4 y − z + 7 = 0 .
B. x − 4 y − z − 7 = 0 . C. x − 4 y − z −18 = 0 . D. x − 4 y − z +18 = 0 . 1
Câu 61: Cho tích phân ( − 2) x x
e dx = a + be  , với ;
a b . Tổng a + b bằng 0 A. 1. B. −3 . C. 5 . D. 1 − . x +1
Câu 62: Có bao nhiêu tiếp tuyến với đồ thị hàm số y = x − , biết tiếp tuyến đó song song với đường 1 thẳng y = 2 − x + 7 ? A. 2 . B. 0 . C. 1. D. 3 .
Câu 63: Hàm số nào dưới đây là hàm số lẻ? A. 2
y = x − 4 − x + 4 .
B. y = 3 − x + 3 + x . C. y = x .
D. y = x − 5x +1 .
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 6 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Câu 64: Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng trung trực của đoạn AB với A(1, 3 − , 2), B( 1 − ,5, 4)
A. x − 4 y − z + 7 = 0 .
B. x − 4 y − z − 7 = 0 . C. x − 4 y − z −18 = 0 . D. x − 4 y − z +18 = 0 . Câu 65: Tính tổng 1 2 3 2018 S = C + C + C +...+ C bằng. 2018 2018 2018 2018 A. 2018 2 . B. 2018 2 −1. C. 2018 2 +1. D. 2019 2 −1.
Câu 66: Cho tam giác ABC có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác ABC bằng A. 12 . B. 3 . C. 6 . D. 24 . 2
Câu 67: Tính tích phân I = (2x + 1)dx  0 A. I = 5 . B. I = 6 . C. I = 2 . D. I = 4 .
Câu 68: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = 4x − x và trục Ox 34 31 32 A. 11. B. . C. . D. . 3 3 3
Câu 69: Cho các số phức z thỏa mãn z = 2 5 . Biết rằng trong mặt phẳng tọa độ các điểm biểu diễn
của số phức w = i + (2 − i) z cùng thuộc một đường tròn cố định. Tính bán kính r của đường tròn đó? A. r = 5 . B. r = 10 . C. r = 20 . D. r = 2 5 .
Câu 70: Phủ định của mệnh đề “ 2 x
  : x  0 ” là mệnh đề nào sau đây? A. 2 x   : x  0 . B. 2 x   : x  0 . C. 2 x   : x  0 . D. 2 x   : x  0 .
Câu 71: Trong mặt phẳng với hệ tọa độ Oxy , nếu phép tịnh tiến theo vectơ v biến điểm ( A 1; 2) thành
điểm B(1; −6) thì nó biến đường thẳng d : 2x − y + 3 = 0 thành đường thẳng d 'có phương trình
A. 2x − y − 3 = 0 .
B. 2x − y = 0 .
C. 2x − y − 8 = 0 .
D. 2x − y − 5 = 0 .
Câu 72: Cho hàm số y = f (x) có tập xác định là \  
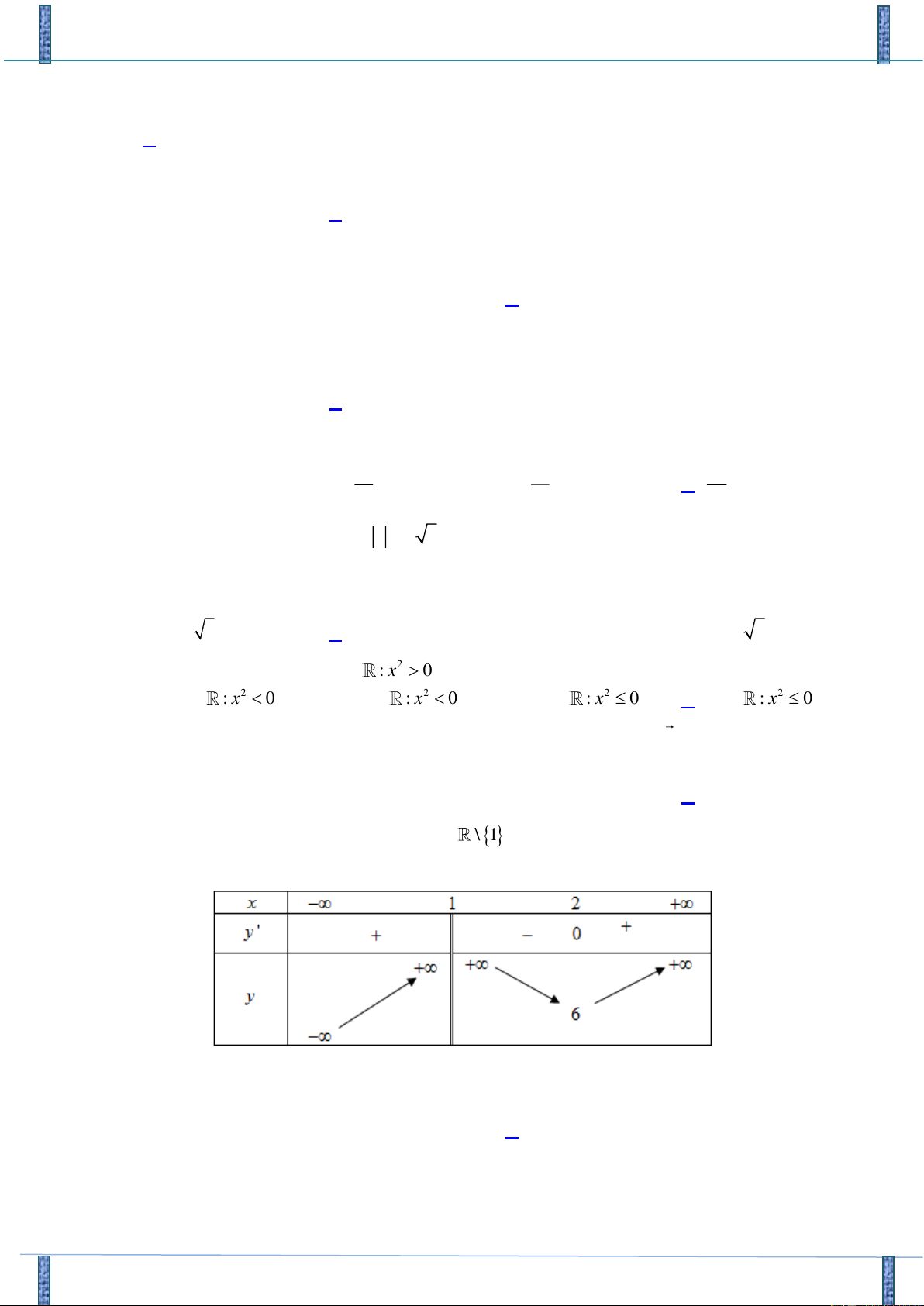
1 và liên tục trên mỗi khoảng xác định của nó.
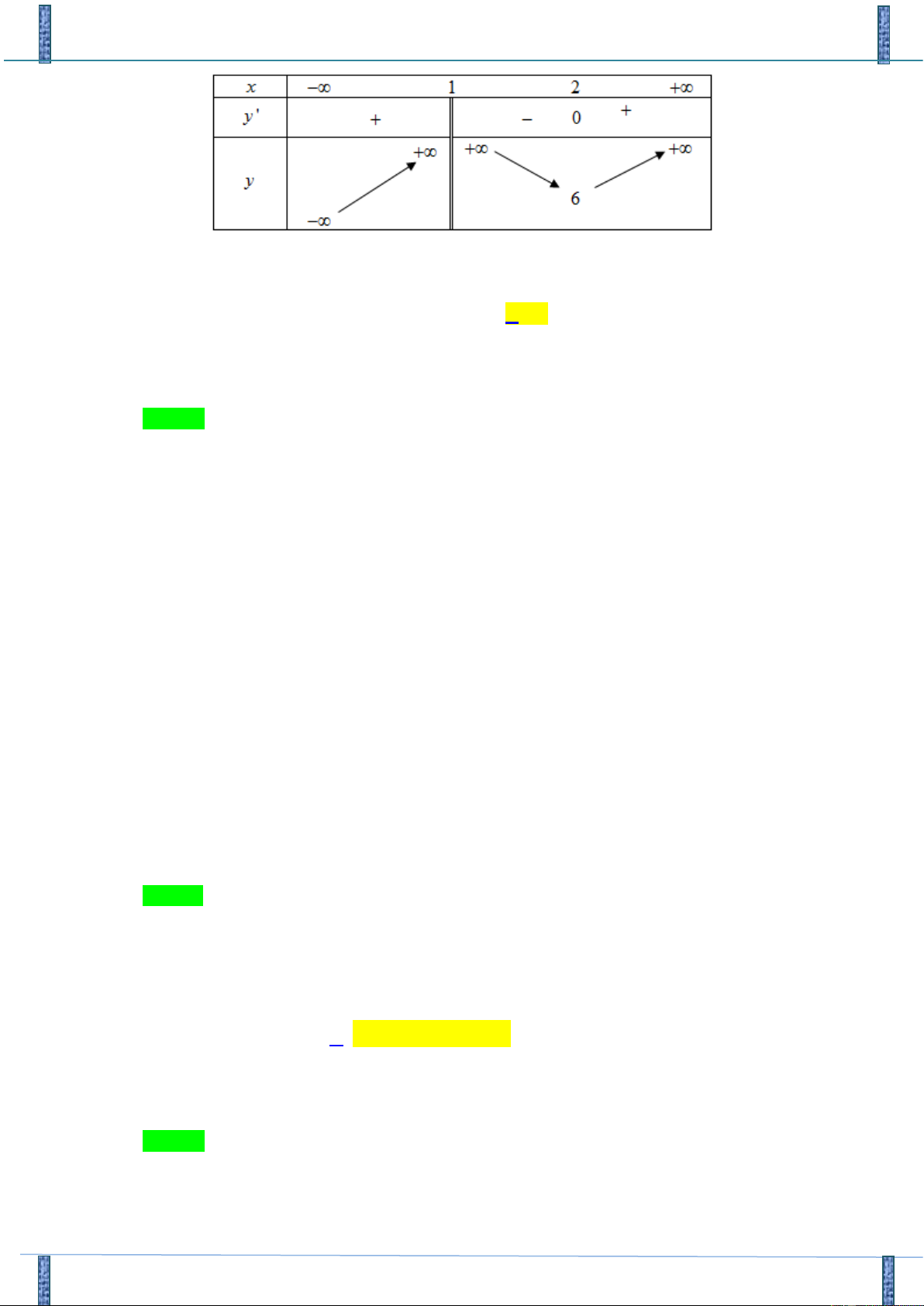
Biết f (x) có bảng biến thiên như sau
Số nghiệm của phương trình f (x) = 6 là A. 0 . B. 1. C. 2 . D. 3 .
Câu 73: Xét trong không gian, mệnh đề nào dưới đây là đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 7 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
B. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì vuông góc với nhau.
Câu 74: Phép quay góc 0
90 biến đường thẳng d thành đường thẳng d ' . Khi đó
A. d ' song song với d . B. d ' trùng d .
C. d ' tạo với d góc 0
60 D. d ' vuông góc với d .
Câu 75: Trong mặt phẳng tọa độ điểm biểu diễn số phức z thỏa mãn z −1− 2i = 3 là
A. đường tròn tâm I (1; 2) , bán kính R = 9 .
B. đường tròn tâm I (1; 2) , bán kính R = 3 .
C. đường tròn tâm I (−1; −2) , bán kính R = 3 . D. đường thẳng có phương trình x + 2 y − 3 = 0 . 8  1 
Câu 76: Trong khai triển của biểu thức 2 − 2x .   Hệ số của 7 x là:  xA. 112 . B. 112 − . C. 1792 − . D. 1792 .
Câu 77: Để lấy nước tưới cây, ông Tráng cần xây một bể chứa nước có dạng hình hộp chữ nhật không
có nắp đậy. Nếu bể cần có thể tích 3
50m và chiều dài gấp 4 lần chiều rộng thì chiều cao bằng
bao nhiêu để chi phí vật liệu thấp nhất. A. 4, 5m . B. 5m. C. 2, 5m . D. 2m
Câu 78: Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d : 2x − 3y + 4 = 0 . Vectơ nào sau đây là
một vectơ chỉ phương của d. 2sin a − cos a
Câu 79: Cho tan a = 2 . Tính giá trị biểu thức P = . sin a + cos a 5 A. P = 2 . B. P = 1 . C. P = . D. P = 1 − . 3
Câu 80: Khẳng định nào sau đây là sai? A. sin ( 
− ) = −sin . B. cot ( 
− ) = −cot . C. cos( 
− ) = −cos . D. tan (  − ) = − tan .
Câu 81: Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d : x − 4y + 15 = 0 và điểm A (2; 0) .
Tìm tọa độ điểm M thuộc d để đoạn AM có độ dài nhỏ nhất. A. M ( 1 − 5;0) . B. M (5; 5) . C. M (0; 3) . D. M (1; 4) .
Câu 82: Thể tích khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là 3 a 3 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 12 4 12 4
Câu 83: Cho tứ diện đều ABCD có độ dài cạnh bằng a . Tính tích vô hướng của hai vectơ AB và CD . 2 a A. A . B CD = 0 . B. 2 A . B CD = a . C. A . B CD = . D. 2 A . B CD =− a . 2
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 8 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Câu 84: Một hộp đựng 9 quả cầu được đánh số lần lượt từ 1 đến 9. Lấy ngẫu nhiên một quả cầu từ hộp
đó. Tính xác suất lấy được quả cầu mang số chẵn. 2 5 4 4 A. . B. . C. . D. . 3 9 5 9
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC. Trang 9 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
SỞ GD&ĐT BẮC GIANG
ĐỀ THI TRẮC NGHIỆM
HỘI ĐỒNG KTKT GIÁO VIÊN MÔN TOÁN THPT NĂM HỌC 2018 - 2019
Thời gian làm bài: 90 phút (80 câu trắc nghiệm) ------------------ MÃ ĐỀ: 385
(Giáo viên không được sử dụng tài liệu)
Họ tên giáo viên: ............................................................................... Ngày sinh: ................. SBD: .................
Trường: ......................................................................................... .... Huyện / thành phố: ...............................
Tuonganh0209@gmail.com Câu 1:
Trong mặt phẳng với hệ trục Oxy , cho hai đường tròn (C ) ( x − )2 2 : 1 + y = 4 và
(C) (x − )2 +( y − )2 : 4 3
=16 cắt nhau tại hai điểm phân biệt A và B . Lập phương trình đường thẳng AB
A. x + y − 2 = 0 .
B. x − y + 2. = 0
C. x + y + 2 = 0 .
D. x − y − 2 = 0 . Lời giải
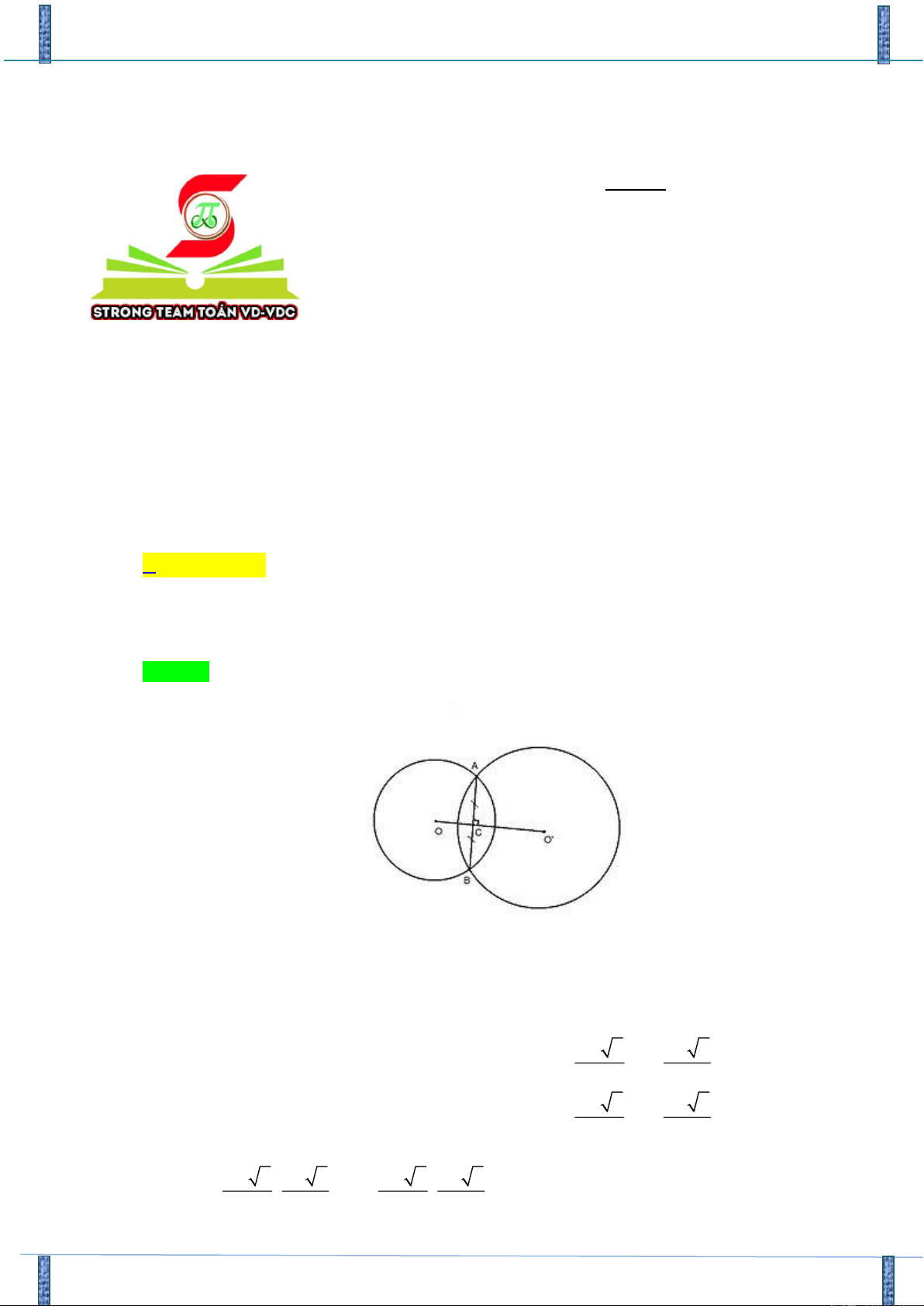
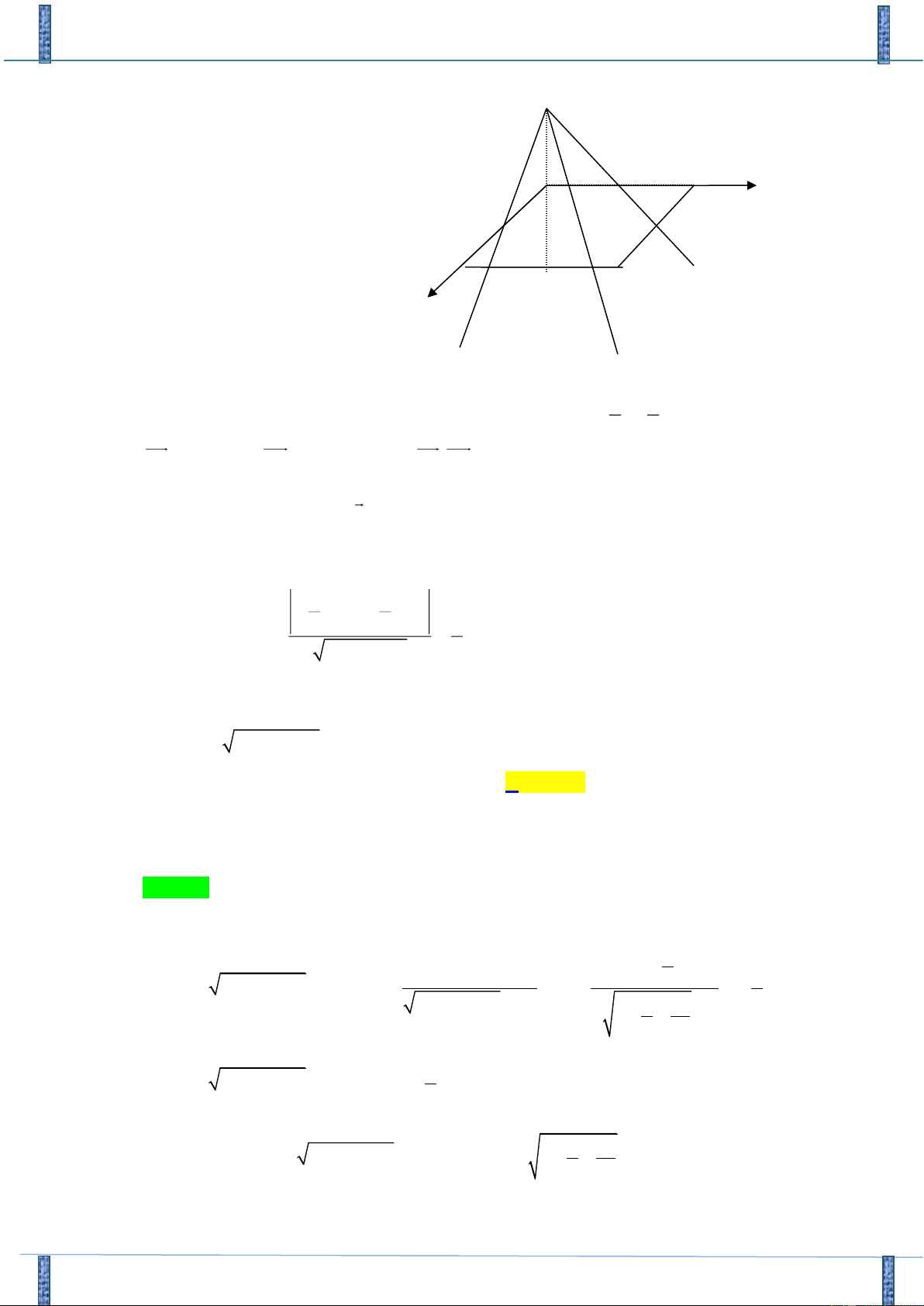
Tác giả: Nguyễn Ngọc Thảo, FB: Nguyễn Ngọc Thảo Chọn A. (  x −  )2 2 2 2 1 + y = 4
x + y − 2x −3 = 0 Cách 1: Xét hệ    (  x −  )2 +( y − )2 2 2 =
x + y −8x − 6y + 9 = 0 4 3 16  3 + 7 1− 7  = − x = , = 2 y y x   y = 2 − x  2 2       2 x +  (2− x)2 2 − 2x − 3 = 0
2x − 6x +1 = 0  3 − 7 1+ 7 x = , y =  2 2  3+ 7 1− 7   3− 7 1+ 7  Suy ra A ,    , B  ,    . 2 2   2 2  
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 10 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
(C) có tâm O(1;0) , (C) có tâm O(4;3)  OO = (3;3)
Nên đường thẳng AB qua A và nhận n (1; ) 1 là vécto pháp tuyến.  +   −  Phương trình: 3 7 1 7 1 x −  +1 y −
 = 0  x + y − 2 = 0     . Chọn A . 2 2     2 2
Cách 2: Giả sử hai đường tròn (C ) ( x − )2 2 :
1 + y = 4 và (C) : ( x − 4) + ( y − 3) = 16 cắt nhau
tại hai điểm phân biệt A và B khi đó tọa độ của A và thỏa mãn hệ phương trình: (  x −  )2 2 2 2 1 + y = 4
x + y − 2x − 3 = 0 (1)    (  x −  )2 +( y − )2 2 2 =
x + y −8x − 6y + 9 = 0 (2) 4 3 16
Lấy (1) trừ (2) ta được: 6x + 6 y −12 = 0  x + y − 2 = 0 là phương trình đường thẳng đi qua 2
điểm A và B Câu 2:
Một hình trụ có diện tích xung quanh bằng 16 và thiết diện qua trục của hình trụ này là một
hình vuông. Thể tích V A. 32 2 . B. 18 . C. 16 . D. 24 . Lời giải
Tác giả: Nguyễn Ngọc Thảo, FB: Nguyễn Ngọc Thảo Chọn C.
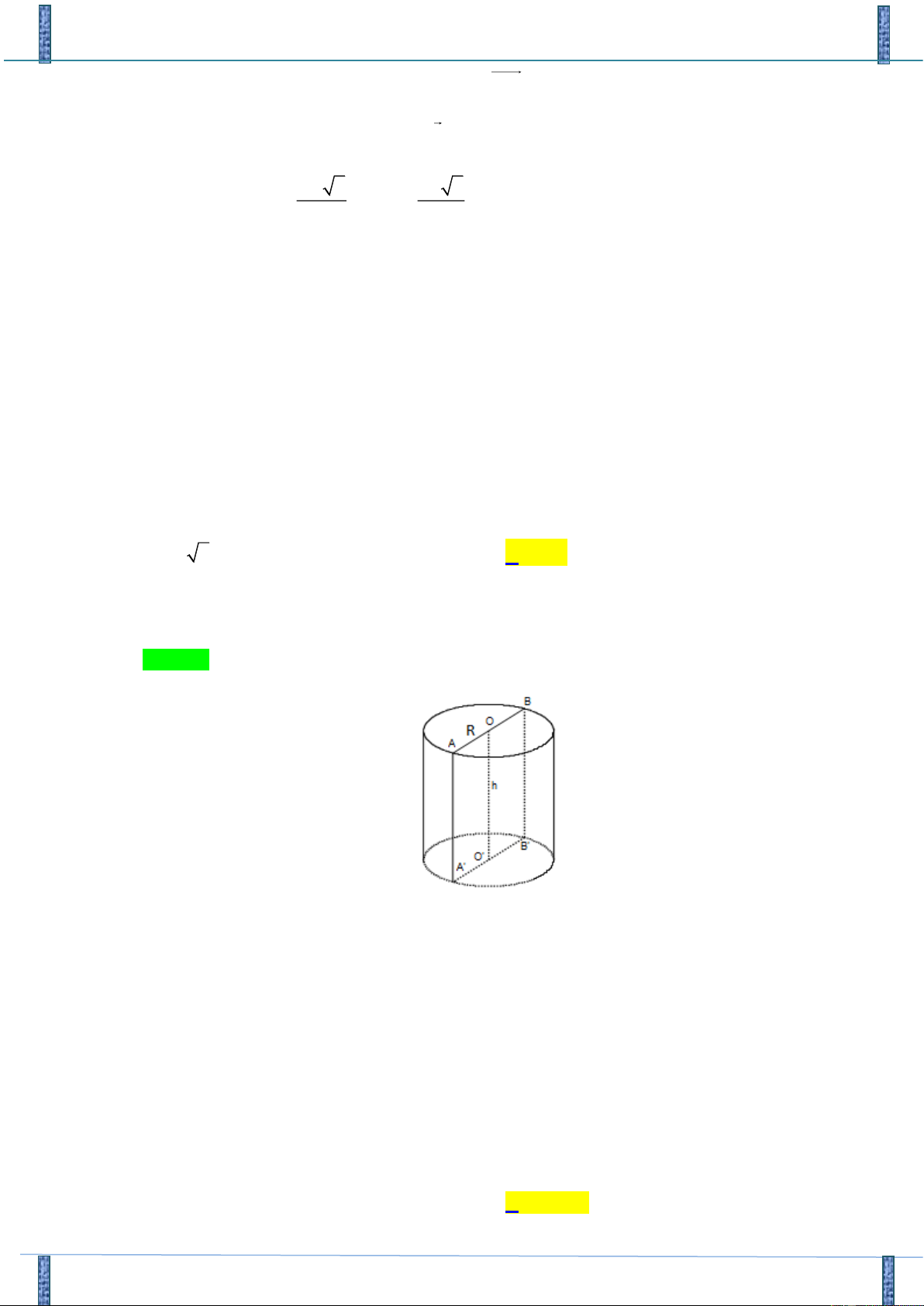
Ta có diện tích xung quanh: S = 2 Rl =16 xq
Thiết diện qua trục là một hình vuông nên: l = 2R = h 2 2
S = 2 Rl =16 = 2.2R R = 4  R = 2 xq Thể tích khối trụ là: 2 2 2
V =  R .h =  .R .2R =  .2 .2.2 = 16 . Chọn C .
buichithanh1987@gmail.com Câu 3:
Một cấp số cộng gồm 5 số hạng. Hiệu số hạng đầu và số hạng cuối bằng 20 . Tìm công sai d
của cấp số cộng đã cho A. d = 5 − . B. d = 4 . C. d = 4 − . D. d = 5. Lời giải
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 11 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Tác giả: Bùi Chí Thanh, FB: Thanh bui Chọn C.
Gọi năm số hạng của cấp số cộng đã cho là: u ;u ;u ;u ;u . 1 2 3 4 5
Theo đề bài ta có: u − u = 20  u − (u + 4d) = 20  d = 5 − 1 5 1 1 Câu 4:
Với hai véc tơ không cùng phương a và b . Xét hai véc tơ u = 2a − 3b và v = a + (x −1)b . Tìm
x để u và v cùng phương. 3 1 1 3 A. x = . B. x = . C. x = − . D. x = − . 2 2 2 2 Lời giải
Tác giả: Bùi Chí Thanh, FB: Thanh bui Chọn B.
Do hai véc tơ a và b không cùng phương nên điều kiện để hai véc tơ u = 2a − 3b và
v = a + (x −1)b cùng phương là: k = 2 2 = k.1  u = kv     1  3 − = k.(x −1) x = −  2
kenbincuame@gmail.com Câu 5:
Giá trị lớn nhất của hàm số y = 2 sin x +1 là 1 A. −1. B. 1. C. − . D. 3 . 2 Lời giải
Tác giả: Nguyễn Việt Thảo, FB: Việt Thảo Chọn D.
Vì sin x  1, x
  nên y = 2sin x +1  3 , x   . 
y = 3 khi sin x = 1  x =
+ k2 , (k  ) . 2
Vậy giá trị lớn nhất của hàm số y = 2 sin x +1 là 3 . Câu 6:
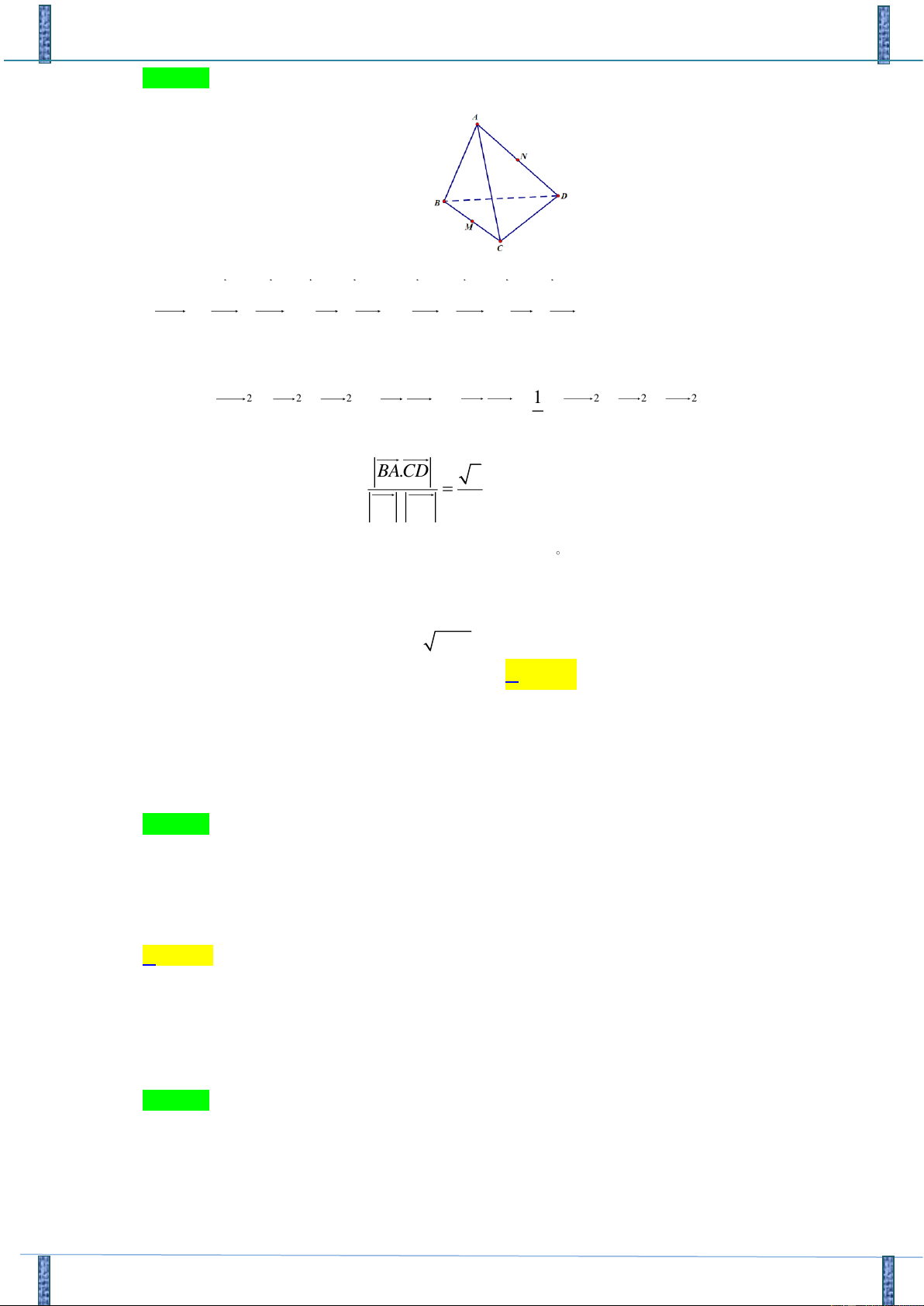
Cho tứ diện ABCD. Gọi M , N lần lượt là trung điểm của BC , AD . Biết AB = 2a ,
CD = 2a 2 và MN = a 5. Số đo góc giữa hai đường thẳng AB và CD là A. 60 . B. 30 . C. 90 . D. 45 . Lời giải
Tác giả: Nguyễn Việt Thảo, FB: Việt Thảo
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 12 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 Chọn D.
Ta có: MN = MB + BA + AN và MN = MC + CD + DN . Suy ra
2MN = (MB + MC) + (BA+ CD) + ( AN + DN ) = BA+ CD (Vì M là trung điểm BC và N là trung điểm AD ). 2 2 2 1 Khi đó 2 2 2
: 4MN = BA + CD + 2 . BA CD B . A CD =
(4MN −BA −CD ) 2 = 4a . 2 BA CD Do vậy ta có: (AB CD) . 2 cos , = = . BA . CD 2
Vậy, số đo góc giữa hai đường thẳng AB và CD là 45 .
hungvn1985@gmail.com Câu 7:
Điều kiện xác định của phương trình x − 2 = 8 − x là
A. x 2;8  . B. x  8 . C. x  2 . D. x  8 . Lời giải
Tác giả: Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn C.
ĐK: x − 2  0  x  2 Câu 8:
Mẹ hơn Minh 25 tuổi. Biết rằng 4 năm về trước tuổi của mẹ gấp 6 lần tuổi của Minh. Hãy
tính tuổi của Minh hiện nay. A. 9 tuổi. B. 5 tuổi. C. 8 tuổi. D. 10 tuổi. Lời giải
Tác giả: Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn A.
Gọi tuổi hiện nay của Minh là x , ( x  0) . Khi đó hiện nay tuổi của mẹ là 25 + x .
Do 4 năm về trước tuổi của mẹ gấp 6 lần tuổi Minh nên ta có
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 13 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
25 + x − 4 = 6(x − 4)  x = 9.
Vậy Minh hiện nay là 9 tuổi.
Phamquoctoan87@gmail.com x x 2
log x − 3log x + 2 = 0 P = x + x Câu 9:
Gọi 1 , 2 là hai nghiệm của phương trình 2 2 . Tính 1 2 . A. 6 . B. 3 − . C. 2 . D. 3 . Lời giải
Tác giả: Phạm Quốc Toàn, FB: Phạm Quốc Toàn Chọn A. log x = 1 x = 2 2
log x − 3log x + 2 = 0 2 1     . 2 2 log x = 2 x = 4  2  2
Vậy P = x + x = 2 + 4 = 6 . 1 2
Phamquoctoan87@gmail.com Câu 10: Cho hàm số 3 2
y = x − 3x − 2x −1 có đồ thị (C ) . Phương trình tiếp tuyến với (C ) tại giao điểm
của (C ) với trục tung là A. y = 2 − x −1.
B. y = 2x −1.
C. y = 2x +1. D. y = 2 − x +1. Lời giải
Tác giả: Phạm Quốc Toàn, FB: Phạm Quốc Toàn Chọn A. Ta có 2
y = 3x − 6x − 2 .
Đồ thị (C ) cắt trục tung tại điểm M (0;− ) 1 .
Phương trình tiếp tuyến với (C ) tại M (0;− )
1 là y = y(0) ( x − 0) + (− ) 1  y = 2 − x −1.
phuongthu081980@gmail.com
Câu 11: Trong mặt phẳng với hệ trục tọa độ ( ;
O i, j ) , cho hai vectơ a = 2i − j b = ( 4 − ;2) và . Khẳng
định nào sau đây là đúng?
A. a và b cùng hướng.
B. a và b ngược hướng. C. a = ( 1 − ;2) . D. a = (2; ) 1 . Lời giải
Tác giả:Nguyễn Thị Phương Thu, FB: Nguyễn Phương Thu Chọn B.
Ta có a = 2i − j a = (2; − ) 1  b = 2 − a
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 14 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
a và b ngược hướng.
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA ⊥ ( ABCD) và
SA = a . Gọi M là trung điểm của cạnh SC . (SBD)
Khoảng cách từ M đến mặt phẳng bằng: a a 4a 2a A. . B. . C. . D. . 2 3 3 3 Lời giải
Tác giả:Nguyễn Thị Phương Thu, FB: Nguyễn Phương Thu Chọn B.
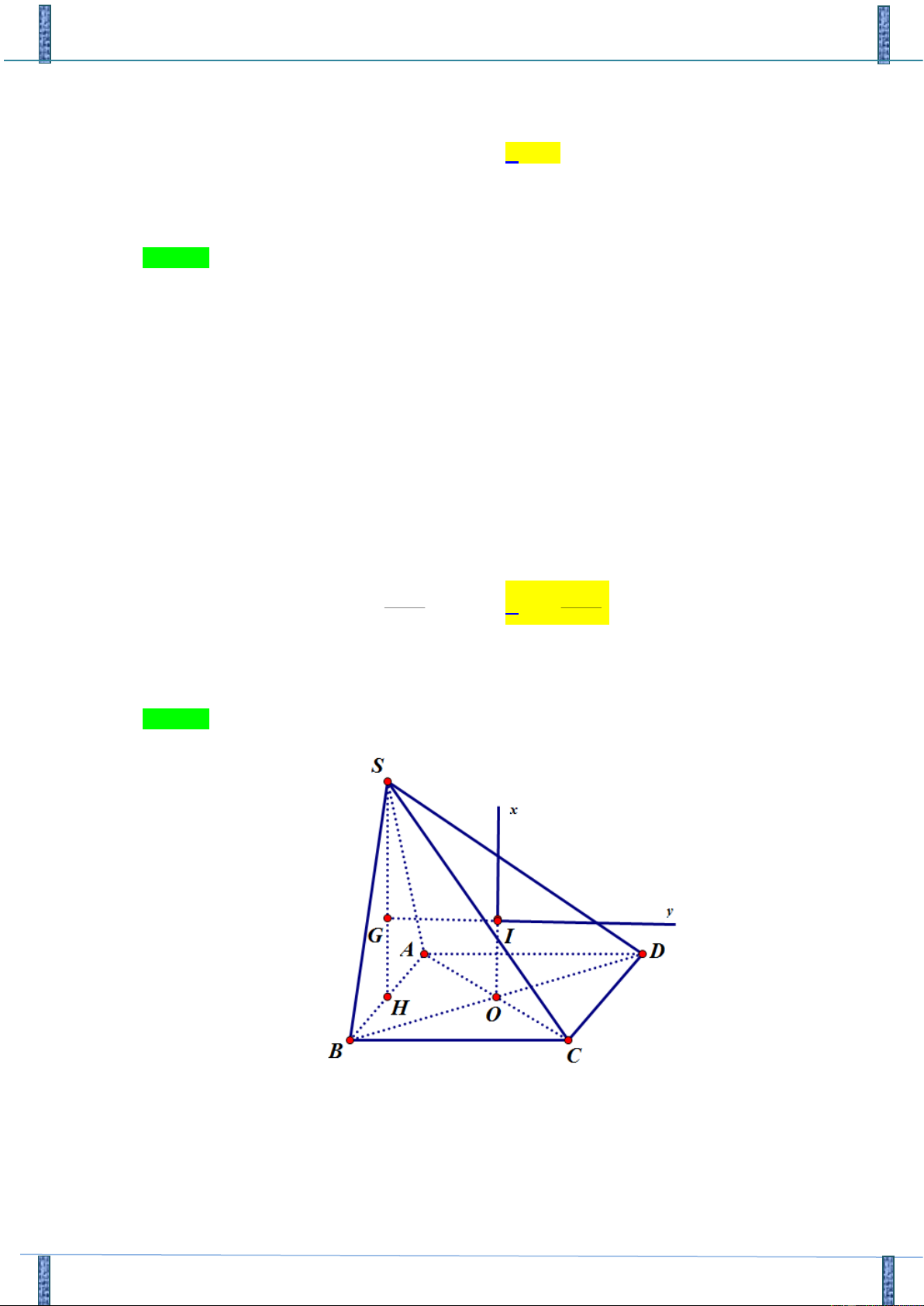
Cách 1: S K G M A D H O B C
AH ⊥ DB, H DB
Ta dựng: AK ⊥ SH,K SH
SA ⊥ ( ABCD)  SA ⊥ BD
BD ⊥ (SAH )  BD ⊥ AK AH ⊥ BD AK ⊥ BD
AK ⊥ (SBD), K (SBD)  d ( ,
A (SBD)) = AKAK ⊥ SH 1 1 1 1 1 5 ABD  : = + = + = 2 2 2 2 AH AB AD a (2a)2 2 4a 1 1 1 5 1 9 2a AHK : = + = + =  AK = 2 2 2 2 2 2 AK AH AS 4a a 4a 3 MG 1 +) SAC
: AM SO = G  = AG 2
d (M , SBD ) AM  ( SBD) ( ) MG 1 = G  = = d ( , A (SBD)) AG 2 ( (SBD)) 1 1 2a a d M , = AK = . = 2 2 3 3
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 15 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 Cách 2: z S M A D y O B C x
Chọn hệ trục tọa độ như hình vẽ: (  a a
A 0; 0; 0), B (a;0;0),C (a; 2a;0); D (0; 2a;0), S (0;0; a)  M ; a;    2 2 
BS = (−a;0; a); DS = (0; 2
− a;a)  BS; DS  =   ( 2 2 2
2a ; a ; 2a )
Suy ra VTPT của (SBD) là n = (2;1; 2) và phương trình mp (SBD) là:
2( x − a) + ( y − 0) + 2( z − 0) = 0  2x + y + 2z − 2a = 0 a a 2. + a + 2. − 2a  ( (SBD)) 2 2 a d M , = = 2 2 2 + + 3 2 1 2
Thutrangtc1@gmail.com Câu 13: Biết ( 2 lim
4x + ax +1 + bx = − . Tính giá của biểu thức 2 3
P = a − 2b . →− ) 1 x A. P = 32 . B. P = 0 . C. P = 16 . D. P = 8 . Lời giải
Tác giả: Nguyễn Thị Thu Trang, FB: Nguyễn Thị Thu Trang Chọn D. TH1: b = 2 1 a + ax + a  lim x
x + ax + + x = = = − x→− ( 1 2 4 1 2 ) lim lim . x→− 2 4x + ax +1 − 2 x x →− a 1 4 − 4 + + − 2 2 x x a
x + ax + + bx = −  − = −  a = . x→− ( 2 lim 4 1 ) 1 1 4 4   a 1
 − neáu b > 2 TH2: b  2  lim
x + ax + + bx = x − + + + b =    x→− ( 2 4 1 ) lim 4 2 x→−  x x  
 + neáu b < 2 Vậy 2 3
a = 4,b = 2  P = a − 2b = 0 .
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 16 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Câu 14: Xếp 6 học sinh gồm 3 học sinh nam và 3 học sinh ngồi vào hai dãy ghế đối diện nhau, mỗi
dãy có 3 ghế (mỗi học sinh ngồi một ghế, các ghế đều khác nhau). Hỏi có bao nhiêu cách xếp
sao cho không có hai học sinh cùng giới ngồi đối diện nhau. A. 720. B. 36. C. 288. D. 72. Lời giải
Tác giả: Nguyễn Thị Thu Trang, FB: Nguyễn Thị Thu Trang Chọn D.
Xếp chỗ ngồi cho bạn nam thứ nhất có 6 cách xếp.
Xếp chỗ ngồi cho bạn nam thứ hai có 4cách xếp (Trừ chỗ của bạn thứ nhất và ghế đối diện).
Xếp chỗ ngồi cho bạn nam thứ ba có 2 cách xếp.
Xếp chỗ ngồi cho 3 bạn nữ có 3! = 6 cách xếp (3 bạn nữ xếp ngẫu nhiên vào 3 chỗ còn lại).
Vậy có 6.4.2.6 = 288 cách xếp chỗ ngồi cho 6 bạn thỏa mãn yêu cầu bài toán.
ptpthuyedu@gmail.com
Câu 15: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy. Tính diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD 2 4 a 2 7 a A. 2 S = 3 a . B. S = . C. S = . D. 2 S = 7 a . 3 3 Lời giải
Tác giả: Phạm Thị Phương Thúy, FB: thuypham Chọn C.
+) Xác định mặt cầu ngoại tiếp hình chóp S.ABCD
Gọi SH là đường cao của tam giác SAB. Vì SAB là tam giác đều và nằm trong mặt phẳng vuông
góc với mặt đáy nên SH là đường cao của hình chóp S.ABCD.
Gọi O là tâm của hình vuông ABCD, từ O dựng Ox ⊥ ( ABCD) .
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 17 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Từ trọng tâm G của tam giác SAB dựng Gy ⊥ (SAB) .
Gọi I = Ox Gy . Vậy I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD .
+) Chứng minh I là tâm mặt cầu cần tìm
Vì I Ox , mà Ox ⊥ ( ABCD) , O là tâm hình vuông ABCD nên I cách đều A, B, C, D (1).
Mặt khác G là trọng tâm của tam giác đều SAB, I Gy , mà Gy ⊥ (SAB) nên I cách đều S, A, B (2).
Từ (1) và (2) suy ra I cách đều S, A, B, C, D. Nên I là tâm mặt cầu ngoại tiếp hình chóp
S.ABCD, bán kính R=IB
+) Tìm độ dài bán kính mặt cầu
Vì OI ⊥ ( ABCD) , SH ⊥ ( ABCD) nên OI / /GH vì G SH (3)
Mặt khác Gy ⊥ (SAB) , I Gy mà OH ⊥ (SAB) (vì OH ⊥ AB, OH ⊥ SH ) nên GI / / O H (4) 1 1 a 3 a 3
Từ (3) và (4) suy ra GHOI là hình bình hành OI = GH = SH = . = . 3 3 2 6
Vì OI ⊥ ( ABCD)  OI ⊥ OB BOI vuông tại B
Xét BOI vuông tại B ta có 2 2  a 3   a 2  7 21 2 2 2 2
IB = IO + OB =   +   = a IB = a = R . 6 2 12 6      7 Diện tích mặt cầu là 2 2 S = 4 R = a . 3
ptpthuyedu@gmail.com
Câu 16: Tìm x để hai vectơ a = ( ;
x 2) và b = (2; 3
− ) có giá vuông góc với nhau. A. 3. B. 0. C. 3 − . D. 2. Lời giải
Tác giả: Phạm Thị Phương Thúy, FB: thuypham Chọn A. Vectơ a = ( ;
x 2) và b = (2; 3
− ) có giá vuông góc với nhau  .
a b = 0  2x − 6 = 0  x = 3 Vậy x = 3.
kimoanh0102@gmail.com x y
Câu 17: Trong mặt phẳng với hệ tọa độ Oxy, cho elip ( E ) 2 2 : +
= 1. Tiêu cự của (E) bằng 25 9 A. 10. B. 16. C. 4. D. 8. Lời giải
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 18 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Tác giả:Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn D. 2 2 Phương x y
trình chính tắc của elip có dạng: +
=1 a  0,b  0 . 2 2 ( ) a ba = 5 Do đó elip (E) có 2 2 
c = a − b = 4 . b  = 3
Tiêu cự của elip (E) bằng 2c = 8 .
Câu 18: Cho hai tập hợp A = −1;3) và B = 1;5 . Giao của A và B là tập hợp nào sau đây? A. −1;5 . B. 1;3) . C. 1;  3 . D. 1;  2 . Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn B.
A B = −1;3) 1;5 = 1;3) .
Quachthuy.tranphu@gmail.com. 1  
Câu 19: Biết các nghiệm của phương trình cos 2x = − có dạng x =
+ k và x = − + k , k  ; 2 m n với ,
m n là các số nguyên dương. Khi đó m + n bằng A. 4. B. 3. C. 5. D. 6. Lời giải
Tác giả: Quách Phương Thúy, FB: Phương Thúy Chọn D.  2   2x = + k2 x = + k 1 2   3 3 cos 2x = −  cos 2x = cos     (k  ) 2 3 2    2x = − + k2 x = − + k  3  3
m + n = 3+ 3 = 6 . 2
Câu 20: Cho số phức z = 1− 2i . Tìm số phức  = 1+ z − z . 1 5 A.  = + i . B.  = 1 − − 6i .
C.  = 5 + 2i .
D.  = 3 − 2i . 2 2 Lời giải
Tác giả: Quách Phương Thúy, FB: Phương Thúy Chọn C.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 19 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
z = 1− 2i z = ( − i)2 2 1 2 = 3
− − 4i  =1+1− 2i +3+ 4i = 5+ 2i
Phản biện: Email: Dangvanquanggb1@gmail.com - FB: DangQuang
trichinhsp@gmail.com
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Giao tuyến của hai mặt
phẳng ( SAB) và ( SCD) là đường thẳng nào dưới đây?
A. Đường thẳng SO .
B. Đường thẳng AC .
C. Đường thẳng đi qua S và song song AB .
D. Đường thẳng đi qua S và song song với AD . Lời giải
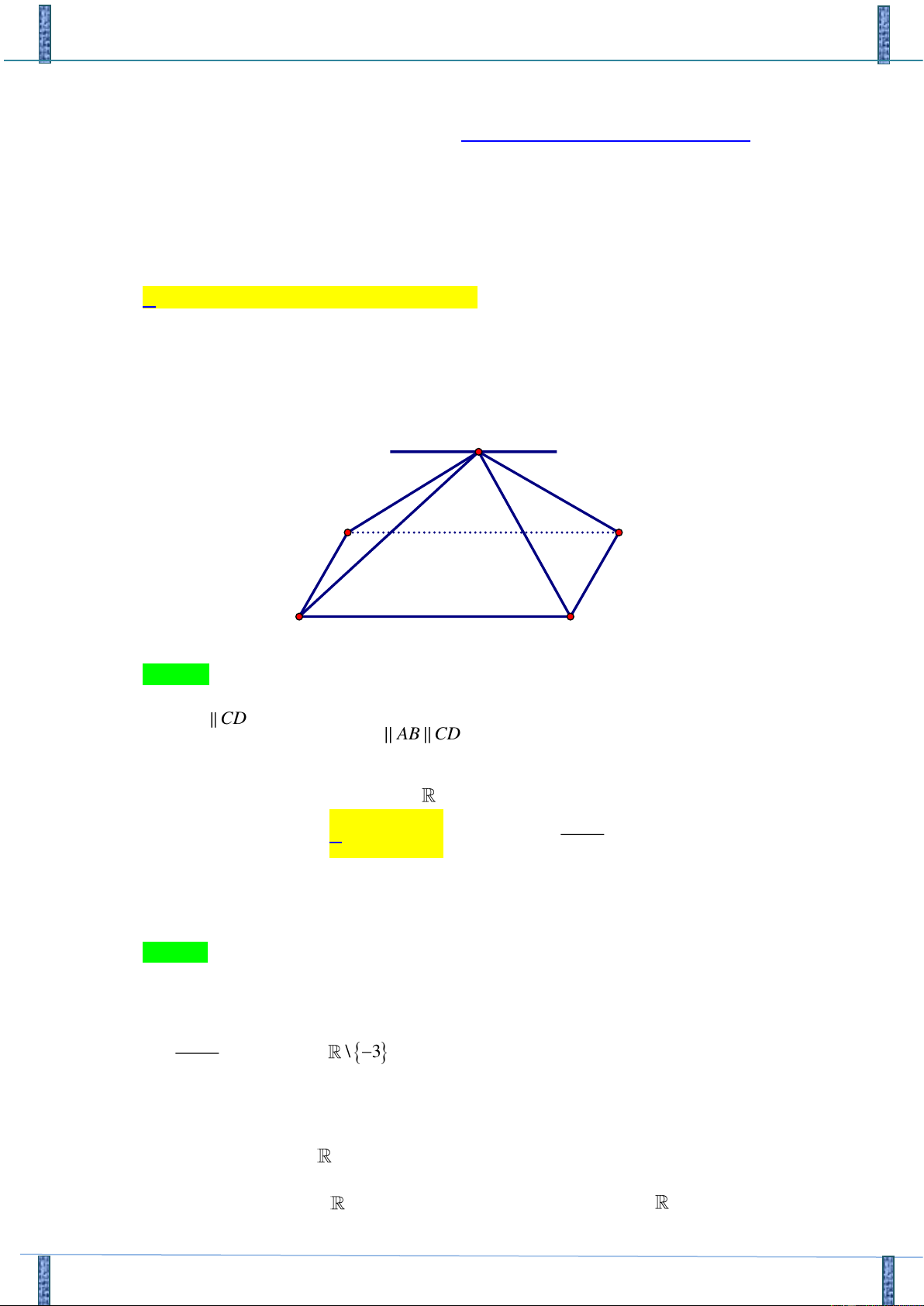
Tác giả: Nguyễn Trí Chính, FB: Nguyễn trí Chính S A B D C Chọn C. AB CD  Có ( . Chọn C  )( )  Sx AB CD SAB SDC = Sx
Câu 22: Hàm số nào dưới đây đồng biển trên ? 2x +1 A. 4 2
y = x + x . B. 3
y = x + 3x . C. y = = − − . x + . D. 3 y x x 3 Lời giải
Tác giả: Nguyễn Trí Chính, FB: Nguyễn trí Chính Chọn B. 4 2
y = x + x có .
a b  0 nên có 1 cực trị (loại) 2x +1 y = có TXĐ D = \ −  3 (loại) x + 3 3
y = −x − x có a  0 (loại) 3
y = x + 3x , TXĐ D = Có / 2
y = 3x + 3  0, x   . Suy ra 3
y = x + 3x luôn đồng biển trên
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 20 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
nvthang368@gmail.com
Câu 23: Biết rằng với mọi giá trị thực của tham số m , các đường thẳng d : y = (m − 2)x + 2m − 3 cùng m
đi qua một điểm cố định là I (a; b) . Tính giá trị của biểu thức: S = a + b A. S = 3 − . B. S = 1 − . C. S = 1. D. S = 3. Lời giải
Tác giả: Nguyễn Văn Thắng, Facebook: Nguyễn Thắng Chọn B.
Ta có phương trình của đường thẳng đã cho: d : y = (m − 2)x + 2m − 3 = (x + 2)m − 2x − 3 m
Vì các đường thẳng d luôn đi qua điểm I nên ta tìm x để m bị triệt tiêu ⇒ I ( 2 − ; 1)  S = 1 − m ⇒ Chọn B
nvthang368@gmail.com
Câu 24: Hàm số nào dưới đây đồng biến trên khoảng (0; + ) ? A. y = log x .
B. y = log x .
C. y = log x .
D. y = log x . 3  e 1 6 3 4 Lời giải
Tác giả: Nguyễn Văn Thắng, Facebook: Nguyễn Thắng Chọn A.
Hàm số y = log x đồng biến trên khoảng (0; + ) ⇔ a  1 ⇒ Chọn A a
tranquocan1980@gmail.com
Câu 25: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S ) có phương trình 2 2 2
x + y + z + 4x − 2 y − 4 = 0 .Tính bán kính R của (S ). A. 1. B. 9 . C. 2 . D. 3 . Lời giải
Tác giả:Trần Quốc An, FB: TranQuocAn Chọn D.
Giả sử phương trình mặt cầu 2 2 2 2 2 2
(S) : x + y + z − 2ax − 2by − 2cz + d = 0 (a + b + c − d  0) Ta có: a = 2
− ,b = 1,c = 0, d = 4 −  Bán kính 2 2 2 R =
a + b + c − d = 3 .
Câu 26: Điểm cực đại của hàm số 3 2
y = x − 3x + 2019 là A. y = 2019 .
B. M (0; 2019) . C. x = 0 . D. x = 2 . Lời giải
Tác giả:Trần Quốc An, FB: TranQuocAn Chọn C.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 21 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019x = 0 Ta có: 2
y = 3x − 6x = 0  x = 2 Bảng biến thiên: x − 0 2 + f (  x) + 0 − 0 + 2019 + f (x) 2015 −
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực đại tại điểm x = 0.
Thuyhung8587@gmail.com
Câu 27: Tập xác định của hàm số y = cot x là:   A.
\ k 2 , k   . B.
\  + k , k   .  2    C.
\ k , k   . D.
\  + k2 , k   .  2  Lời giải
Tác giả: Cấn Việt Hưng, FB: Viet Hung Chọn C.
+)Điều kiện: sin x  0  x k , k  , suy ra tập xác định của hàm số y = cot x là D =
\ k , k  .
Thuyhung8587@gmail.com
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : x + y − z −1 = 0 và đường thẳng x + 2 y − 4 z +1 d : = = 2 2 −
. Viết phương trình đường thẳng d  là hình chiếu vuông góc của d trên 1 (P) . x + 2 y z +1 x − 2 y z −1 A. d : = = d : = = 7 5 − . B. 2 7 5 − . 2 x + 2 y z +1 x − 2 y z −1 C. d  : = = . D. d  : = = . 7 5 2 7 5 2 Lời giải
Tác giả: Cấn Việt Hưng, FB: Viet Hung Chọn B.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 22 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 d N M M' d' Px = −2 + 2t
+) Phương trình tham số của d : y = 4 − 2t , t R . Gọi M = (−2 + 2t;4 − 2t; 1 − + t ) là giao z = −1+ t
điểm của d và (P)  (−2 + 2t) + (4 − 2t) − (−1+ t) −1 = 0  t = 2  M = (2;0; ) 1 .
+) Mặt phẳng ( P) có 1 vector pháp tuyến là n = (1;1; − )
1 . Điểm N = (0; 2;0) d . P
Gọi  là đường thẳng qua N (0; 2; 0) và vuông góc với mặt phẳng ( P)   nhận vector n = (1;1; − )
1 làm vector chỉ phương. Suy ra phương trình của  là: Px = c
( ) x −0 y − 2 z −0   : = =
 () : y = 2 + c , cR . Gọi M  = ( ; c 2 + ;
c −c) là giao điểm của  1 1 1 − z = −c   
với mặt phẳng ( P)  c + ( + c) − (−c) 1 2 −1 = 0  c = − 1 5 1  M  − ; ;   . 3  3 3 3   7 5 2  +) MM  = − ; ; − 
 , đường thẳng d là hình chiếu vuông góc của d trên mặt phẳng (P)  3 3 3 
nên d  chính là đường thẳng MM ' , suy ra d  đi qua M (2; 0; ) 1 và nhận vector u = 3 − MM  = (7; 5
− ;2) làm vector chỉ phương nên phương trình của d là: x − 2 y z −1 d : = = 7 5 − . 2
luongthanh80tm@gmail.com
Câu 29: Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai điểm A(−3; 4) và B (5;6) . Trung điểm của
đoạn thẳng AB có tọa độ là A. (1;5) . B. (4; ) 1 . C. (5; ) 1 . D. (8; 2) . Lời giải
Tác giả: Nguyễn Lương Thành, FB: Luong Thanh Nguyen Chọn A.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 23 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019x + x −3 + 5 A B x = = = 1  I  2 2
Gọi I là trung điểm của đoạn thẳng AB . Khi đó ta có:   I (1;5) . y + y 4 + 6  A B y = = = 5 I  2 2
Câu 30: Một nguyên hàm của hàm số f ( x) 2 = 3x là A. ( ) 3
F x = x + x . B. F ( x) 3 = x +1.
C. F ( x) = 6x . D. F ( x) 3 = 3x . Lời giải
Tác giả: Nguyễn Lương Thành, FB: Luong Thanh Nguyen Chọn B. Ta có: f  (x) 2 3
dx = 3x dx = x + C
với C là một hằng số.
Do đó các phương án A, C, D bị loại.
Ta chọn phương án B (trong trường hợp C = 1).
vannguyen30031981@gmail.com
Câu 31: Cho tam giác ABC . Khẳng định nào sau đây là sai?
A. AB − AC = CB .
B. AB + BA = 0 .
C. AB − AC = BC .
D. AB + BC = AC . Lời giải
Tác giả: Nguyễn Thị Vân, FB: Vân Nguyễn Thị Chọn C.
Theo quy tắc về hiệu hai véc tơ ta có: AB − AC = CB nên khẳng định C sai. x
Câu 32: Tập xác định của hàm số f ( x) = là 2 x −1
A. 0; +) \   1 . B. (1; +) . C. 0; ) 1 . D. \ −1;  1 . Lời giải
Tác giả: Nguyễn Thị Vân, FB: Vân Nguyễn Thị Chọn A. x  0 x  0  x  0
Điều kiện xác định: 
 x  −1  2 x −1  0  x  1 x  1 
Vậy tập xác định của hàm số là 0; +) \   1 .
hanhkeo@gmail.com
Câu 33: Bảng biến thiên nào dưới đây là của hàm số 2
y = −x + 2x + 2 ? A. B.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 24 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 x − + x − −1 + + − y y 1 − − − C. D. x − 1 + x − 1 + + + y 3 y − − 3 Lời giải
Tác giả: Nguyễn Hồng Hạnh, FB: Nguyễn Hồng Hạnh Chọn C. y ' = 2 − x + 2
y ' = 0  x = 1
Hàm số đồng biến trên ( ; − )
1 ; nghịch biến trên (1; + ) . Chọn C.
hanhkeo@gmail.com
Câu 34: Đạo hàm của hàm số f ( x) 2 = sin x là:
A. f '( x) = 2sin x .
B. f '( x) = 2 cos x .
C. f '( x) = − sin (2x) . D. f '( x) = sin (2x) . Lời giải
Tác giả: Nguyễn Hồng Hạnh, FB: Nguyễn Hồng Hạnh Chọn D. f '( x) = 2sin .
x (sin x)' = 2sin .
x cos x = sin 2x . Chọn D.
nongdansanhdieu.tk@gmail.com 2  x − 4  khi x  2 −
Câu 35: Tìm m để hàm số f (x) =  x + 2
liên tục tại x = 2 −  m khi x = 2 − A. m = 4 − . B. m = 2 . C. m = 4 . D. m = 0 . Lời giải
Tác giả: Nguyễn Tuấn Đạt, FB: Nguyễn Đạt Chọn A. 2  x − 4 
Hàm số liên tục tại x = 2 − khi và chỉ khi lim 
 = lim m = m m = 4 − Chọn A. x→ 2 − x→−2  x + 2 
nongdansanhdieu.tk@gmail.com
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 25 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 x −
Câu 36: Tìm tất cả các giá trị của tham số m để đồ thị của hàm số 3 9
y = x + có tiệm cận đứng m A. m  3 − . B. m  3 . C. m = 3 . D. m = 3 − . Lời giải
Tác giả: Nguyễn Tuấn Đạt, FB: Nguyễn Đạt Chọn A. Tập xác định D = \ −  m
Dễ dàng chọn được A
Giachuan85@gmail.com 2019 2018 − + +
Câu 37: Tính lim( 2n 3n 4) ? A. − . B. + . C. 2 − . D. 2019 . Lời giải:
Họ và tên: Trần Gia Chuân Chọn A.   3 4  Ta có lim ( 2019 2018 2 − n + 3n + 4) 2019 = lim n . 2 − + + = −    . 2019   n n  u  = 2  1
Câu 38: Cho dãy số (U xác định bởi  Tính u ? n ) * 10 u
= u + 5, nNn 1+ n A. 57 . B. 62 . C. 47 . D. 52 . Lời giải:
Họ và tên: Trần Gia Chuân Chọn C.
Cách 1 : Dùng casio 570VN
B1 : Nhập vào máy tính “2”=>SHIFT=>STO=>A
B2: Nhập B = A + 5 : A = B
B3: Ấn CALC rồi bấm liên tiếp dấu “=” cho kết quả u = 47 . 10 u  = 2  1 Cách 2 : Từ  . * u
= u + 5, nNn 1+ n Ta có u
−u = 5 nên dãy (U là một cấp số cộng với công sai d = 5 nên n ) n 1 + n
u = u + 9d = 2 + 45 = 47 . 10 1
cvtung.lg2@bacgiang.edu.vn
Câu 39: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình  x  1+ tan x tan
sin x + cot x = 4   là  2 
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 26 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019     A. − . B. . C. . D. − . 6 2 6 2 Lời giải
Tác giả: Cao Văn Tùng, FB: Cao Tung Chọn D. cos x  0  Điều kiện 
 sin 2x  0  x k ,k  s  in x  0 2 x x sin x sin + cos x cos  x  2 2 1+ tan x tan
sin x + cot x = 4 
sin x + cot x = 4    2 x  cos x cos 2 x cos 2 
sin x + cot x = 4  tan x + cot x = 4 2
 tan x − 4 tan x +1 = 0 x cos x cos 2   5 tan x = 2 + 3 = +   x k   12 1    . tan x = 2 − 3 =    2 + 3  x = + l  12 
Với hai họ nghiệm trên dễ thấy nghiệm dương nhỏ nhất là
; để được nghiệm âm lớn nhất ta 12 7 −  11 −  7 − 
đều cho k = l = 1 − được nghiệm âm ;
khi đó nghiệm âm lớn nhất là . 12 12 12 7 −    Ta có + = − . 12 12 2 log 5
Câu 40: Với a  0; a  1 , giá trị của biểu thức a a là 1 A. 5 . B. 5 . C. 25 . D. . 5 Lời giải
Tác giả: Cao Văn Tùng, FB: Cao Tung Chọn C. Ta có a a = = ( a a a a )2 log 5 2log 5 log 5 2 = 5 = 25
maihuongpla@gmail.com
Câu 41: Cho hình chóp S.ABC có SA = 6 , SB = 5 , SC = 4 , 0 0
ASB = BSC = 45 , ASC = 60 . Tính thể
tích khối chóp S.ABC . A. V = 16 . B. V = 10 . C. V = 14 . D. V = 12 .
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 27 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 Lời giải
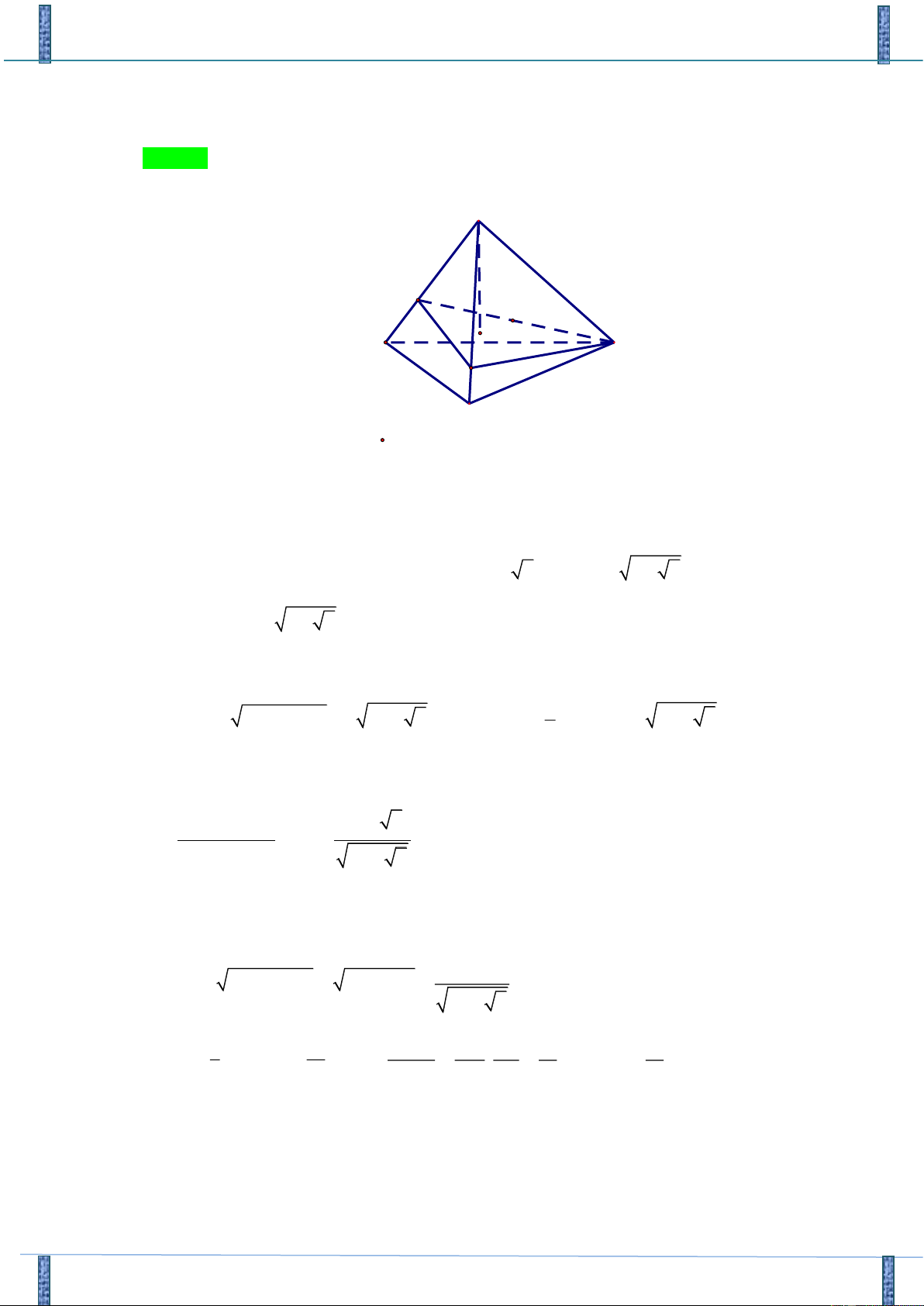
Tác giả: Đặng Mai Hương. FB: maihuongpla Chọn B. S M E A C O N B Lấy M  ,
SA N SB sao cho SM = SN = 4
Áp dụng định lý cosin cho tam giác SMN 2 2 2
MN = SM + SN − 2SM .SN.cos MSN = 32 −16 2  MN = 4 2 − 2
Tương tự CN = 4 2 − 2
Gọi E là trung điểm của CM , tam giác NCM cân tại N nên NE ⊥ CM 1 ta có 2 2 NE =
NC − CE = 2 7 − 4 2 suy ra S
= MC.NE = 4 7 − 4 2 NCM 2
Gọi R là bán kính đường tròn ngoại tiếp tam giác NCM ta có: 4 − NC NM CM (2 2 . . ) R =  R = 4.SNCM 7 − 4 2
Vì SC = SM = SN = 4suy ra hình chiếu của S trên mp (NCM ) trùng với tâm O đường tròn
ngoại tiếp tam giác NCM 4 2 2 2 2
h = SO = SN − ON = SN − R = 7 − 4 2 1 16 V SM SN 8 15 V = S . O S = . Ta có S.NMC = . =  V = V = 10 S .NMC 3 NCM 3 S . ABC S . V SA SB 15 8 NMC S . ABC
Cách 2 : ( Dùng cho trắc nghiệm)
Đặt SA = 6 = a , SB = 5 = b , SC = 4 = c , 0 0 0
BSC = x = 45 ; ASC = y = 60 ; ASB = z = 45 .
Ta có thể tích khối chóp S.ABC là :
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 28 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 abc 2 2 2 V = . 1+ 2 cos . x cos . y o
c sz − cos x − cos y − o c s z 6 6.5.4 0 0 0 2 0 2 0 2 0 = . 1+ 2 cos 45 .cos 60 . o
c s45 − cos 45 − cos 60 − o c s 45 = 10 6
Câu 42: Bất phương trình 2
−x + 2x + 3  0 có tập nghiệm là A. ( ; − − )
1  (3; +) . B. ( 1 − ;3) . C. −1;3 . D. (−3; ) 1 . Lời giải
Tác giả: Đặng Mai Hương. FB: maihuongpla Chọn B. Ta có: 2
−x + 2x + 3  0  1 −  x  3
Ducchinh2308@gmail.com
Câu 43: Khẳng định nào sau đây là đúng?
A. a b a + c b + c . B. 2 2
a b a b . a b
C. a b ac bc .
D. a b   . c c Lời giải
Tác giả: Huỳnh Đức Chính, FB: Huỳnh Đức Chính Chọn A.
Theo tính chất của bất đẳng thức (cộng hai vế của một bất đẳng thức với cùng một biểu thức). Giải thích thêm :
- Khẳng định B sai. Ví dụ: a = 2 − ;b = 1 . Ta có 2 − 1 nhưng (− )2 2 2 1 .
- Khẳng định C sai. Ví dụ: a = 2; b = 3; c = −1. Ta có 2  3 nhưng 2.(− ) 1  3.(− ) 1 . 2 3
- Khẳng định D sai. Ví dụ: a = 2;b = 3; c = −1 . Ta có 2  3 nhưng  1 − 1 − .
Câu 44: Tính diện tích xung quanh của một hình nón có bán kính đáy bằng 4cm và chiều cao bằng 3cm A. 2 S = 20 cm . B. 2 S = 18 cm . C. 2 S = 15 cm . D. 2 S = 12 cm . xq xq xq xq Lời giải
Tác giả: Huỳnh Đức Chính, FB: Huỳnh Đức Chính Chọn D.
Đường sinh của hình nón: 2 2 l =
r + h = 5cm .
Diện tích xung quanh của hình nón: 2 S
=  rl = 20 cm . xq
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 29 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
vuhangltt@gmail.com
Câu 45: Khối bát diện đều có bao nhiêu cạnh? A. 1. B. 8 .. C. 20 . D. 12 . Lời giải
Tác giả: Vũ Thị Hằng, FB: Đạt Lâm Huy
Khối bát diện đều có 12 cạnh Chọn D.
Câu 46: Mô đun của số phức z = 3 + 4i là A. 4 . B. 7 . C. 3 . D. 5 Lời giải
Tác giả: Vũ Thị Hằng, FB: Đạt Lâm Huy Chọn D. 2 2 z = 3 + 4 = 5.
hientam112@gmail.com
Câu 47: Có bao nhiêu số tự nhiên có hai chữ số mà cả hai chữ số đó đều lẻ? A. 20. B. 50. C. 25. D. 45. Lời giải
Họ và tên: Bùi Thị Thu Hiền- Fb Hiền Tấm Chọn C.
- Gọi số tự nhiên có hai chữ số cần lập thỏa mãn yêu cầu bài toán là ab ( a, b 1;3;5;7;  9 )
+ a: có 5 cách chọn + b: có 5 cách chọn.
Dó đó có: 5 x 5 = 25 cách lập số có 2 chữ số mà cả hai chữ số đều lẻ. Chọn C.
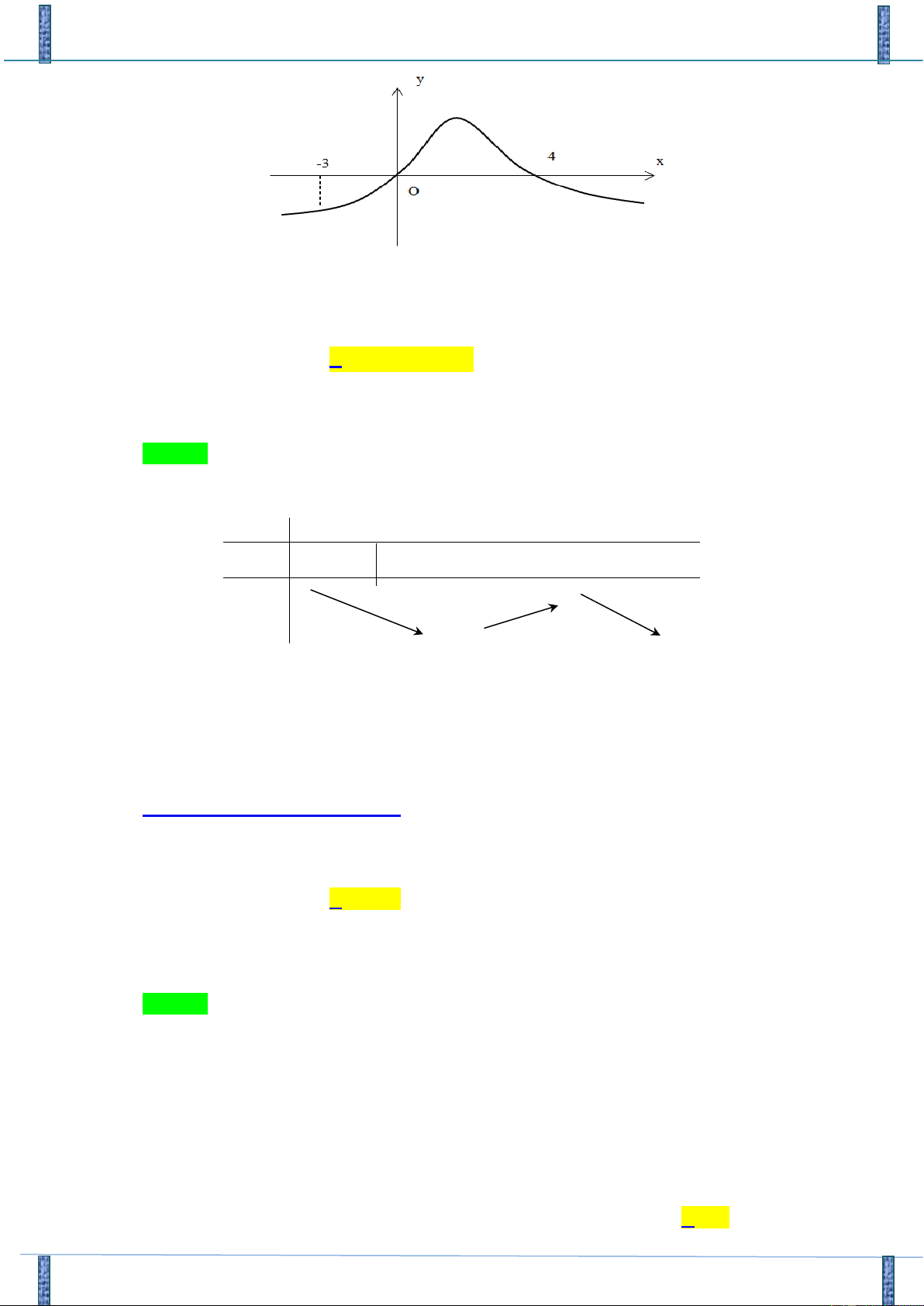
Câu 48: Cho hàm số f ( x) có đạo hàm trên
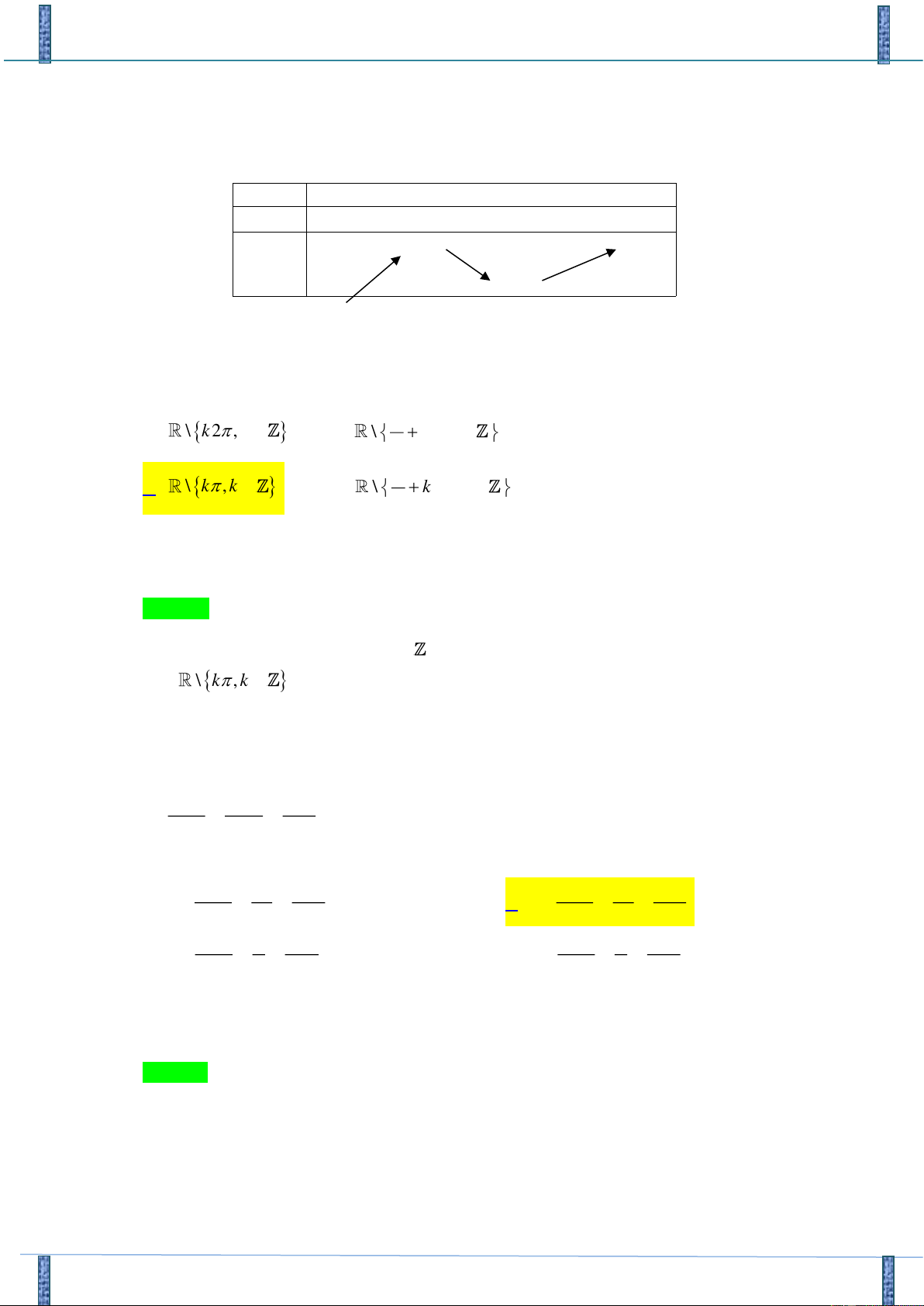
và có đồ thị của hàm y = f ( x) được cho như hình vẽ.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 30 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Biết rằng f (−3) + f (0) = f (4) + f (− )
1 . Giá trị lớn nhất và giá trị nhỏ nhất của f ( x) trên
đoạn −3;4 lần lượt là:
A. f (4) và f (−3) .
B. f (−3) và f (0) .
C. f (4) và f (0) .
D. f (2) và f (−3) .
Họ và tên: Bùi Thị Thu Hiền- Fb Hiền Tấm Lời giải Chọn B.
Dựa vào đồ thị của hàm số y = f ( x) ta có bảng biến thiên của hàm số y = f ( x) : x − -3 0 4 + f ( x) − − 0 + 0 − f (4) f ( x) f (−3) f (0)
f (0) = f (4) = 0 nên x = 0 và x = 4 là hai điểm cực trị của y = f ( x) .
Từ bảng biến thiên ta có min f (x) = f (0) , đồng thời f (− ) 1  f (0) . Do đó:  3 − ;4
f (−3) + f (0) = f (4) + f (− )
1  f (−3) − f (4) = f (− )
1 − f (0)  0  f (−3)  f (4) .
 max f (x) = f ( 3
− ) . Chọn B  3 − ;4
nguyentuanblog1010@gmail.com
Câu 49: Tìm tất cả các giá trị của tham số m để phương trình 2
x − 2x + m −1 = 0 có hai nghiệm trái dấu. A. m  2 . B. m  1. C. m  1. D. m  2 . Lời giải
Tác giả: Phạm Chí Tuân, FB: Tuân Chí Phạm Chọn B. Xét phương trình 2
x − 2x + m −1 = 0 ( ) 1 . Phương trình ( )
1 có hai nghiệm trái dấu khi và chỉ khi: ac  0  1.(m − ) 1  0  m  1.
Câu 50: Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn (C ) x + ( y + )2 2 : 2
= 36 . Khi đó phép vị tự
tỉ số k = 3 biến đường tròn (C ) thành đường tròn (C ') có bán kính là: A. 108 . B. 12 . C. 6 . D. 18 .
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 31 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 Lời giải
Tác giả: Phạm Chí Tuân, FB: Tuân Chí Phạm Chọn D.
Theo tính chất của phép vị tự thì phép vị tự tỉ số k biến đường tròn có bán kính R thành
đường tròn có bán kính k R .
Áp dụng vào bài toán ta có phép vị tự tỉ số k = 3 biến đường tròn (C ) có bán kính R = 6 thành
đường tròn (C ') có bán kính R ' = k .R = 3 .6 = 18 .
Câu 51: Bất phương trình ( x − ) 1
x  0 có bao nhiêu nghiệm nguyên thuộc −1; 2018 ? A. 1. B. 2. C. 2019. D. 2018. Lời giải
Tác giả: Nguyễn Văn Mộng, FB: Nguyễn Văn Mộng Chọn C. x  0   x  0 x −1 0  x = 0 Ta có: ( x − ) 1 x  0     x  0 x 1   x  0 x−1 0 
Xét nghiệm nguyên của bất phương trình đã cho trên −1; 2018 thì x 0;1; 2;...; 201  8
Do đó, số nghiệm nguyên của bất phương trình đã cho là: 2018 − 0 +1 = 2019. Vậy ta chọn C.
Câu 52: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của
OB , ( ) là mặt phẳng đi qua M , song song với AC và song song với SB . Thiết diện của
hình chóp S.ABCD khi cắt bởi mặt phẳng ( ) là hình gì? A. Lục giác. B. Ngũ giác. C. Tam giác. D. Tứ giác. Lời giải
Tác giả: Nguyễn Văn Mộng, FB: Nguyễn Văn Mộng Chọn B.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 32 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 Ta có: M   ( )( ABCD)   ( ) ( ABCD) (
= đi qua M và song song với AC .  ABCD  )  AC ( ) d1 / /
Trong ( ABCD) , gọi I, H lần lượt là giao điểm của d với AB và BC . Khi đó, I và H lần 1
lượt là trung điểm của AB và BC . Ta lại có: I   ( )(SAB)   ( ) ( AB) ( =
đi qua I và song song với SB .  SAB  )  SB ( ) d2 / /
Trong ( SAB) , gọi J là giao điểm của d với SA . Khi đó, J là trung điểm của SA . 2 Ta cũng có: H   ( )(SBC)   ( ) (SBC) ( =
đi qua H và song song với SB .  SBC  )  SB ( ) d3 / /
Trong ( SBC ) , gọi L là giao điểm của d với SC . Khi đó, L là trung điểm của SC . 3 Mặt khác: M   ( )(SBD)   ( ) (SBD) ( =
đi qua M và song song với SB .  SBD  )  SB ( ) d4 / /
Trong ( SBC ) , gọi K là giao điểm của d với SD . 4
Vậy thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng ( ) là ngũ giác HIJKL .
nhungcvp95@gmail.com
Câu 53: Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a = (2;1; 2
− ) và vectơ b = (1;0;2) .
Tìm tọa độ vectơ c là tích có hướng của a và b .
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 33 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
A. c = (2;6;− ) 1 .
B. c = (4;6;− ) 1 . C. c = (4; 6 − ;− ) 1 . D. c = (2; 6 − ;− ) 1 . Lời giải
Tác giả: Phùng Nhung, FB: Phùng Nhung Chọn D.
Áp dụng công thức tính tích có hướng trong hệ trục tọa độ Oxyz ta được:
c = a,b = (2; 6 − ;− ) 1  
Vậy chọn đáp án D.
nhungcvp95@gmail.com
Câu 54: Phương trình 3x − 2 = x có bao nhiêu nghiệm nguyên? A. 3. B. 0. C. 2. D. 1. Lời giải
Tác giả: Phùng Nhung, FB: Phùng Nhung Chọn D. Ta có:   2 
3x − 2 = x x     x =1  3 
3x − 2 = x     1   2  x =
2 − 3x = x x      2   3 
Vậy số nghiệm nguyên của phương trình là 1.
xuanmda@gmail.com −
Câu 55: Nghiệm của phương trình x 3 2
= 4 thuộc tập nào dưới đây? A. 5;8. B. ( ; − 0 . C. (0;5) . D. (8; +) . Lời giải Chọn A. x−3 x−3 2 2 = 4  2
= 2  x − 3 = 2  x = 55;8
Câu 56: u được cho bởi công thức nào dưới đây là số hạng tổng quát của một cấp số nhân? n 1 1 1 1 A. u = . B. 2 u = n − . C. u = −1. D. 2 u = n + . n n 1 2 + n 2 n 2n n 2 Lời giải Chọn A.
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 34 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 n 1 − 1 1  1  1 1 u = = .
là số hạng tổng quát của một cấp số nhân có u = và q = . n   n 1 2 + 4  2  1 4 2 1 1 7 1 17 7 2 u = n − có u = ;u = = .7;u =
 .7 nên không phải số hạng tổng quát của một n 2 1 2 3 2 2 2 2 2 cấp số nhân. 1 1 3 1 3 7 3 3 u =
−1có u = − ;u = − = − . ;u = −  − . nên không phải số hạng tổng quát n 2n 1 2 3 2 4 2 2 8 4 2 của một cấp số nhân. 1 3 9 3 19 9 2 u = n + có u = ;u = = .3;u =
 .3 nên không phải số hạng tổng quát của một n 2 1 2 3 2 2 2 2 2 cấp số nhân.
diephd02@gmail.com 1
Câu 57: Cho tích phân ( − 2) x x
e dx = a + be  , với ;
a b . Tổng a + b bằng 0 A. 1. B. −3 . C. 5 . D. 1 − . Lời giải
Họ và tên: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn A. Đặt
u = x − 2 du = 1 1 dx 1 1   x e d x e e d e e a be x
 ( − 2) x x = ( − 2) x −
x x= − + 2 − x = 3 − 2e = + x  0  dv = e dx v = 0 e 0 0 với ;
a b  a = 3,b = −2  a + b = 1 x +1
Câu 58: Có bao nhiêu tiếp tuyến với đồ thị hàm số y = x − , biết tiếp tuyến đó song song với đường 1 thẳng y = 2 − x + 7 ? A. 2 . B. 0 . C. 1. D. 3 . Lời giải
Họ và tên: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn C. x +1 2 − y =  y = 2 x −1 (x − . 1) x +1
Phương trình tiếp tuyến tại điểm M (x ; y ) của đồ thị hàm số y = 0 0 0 x − có dạng: 1
y − y = y (x − x ) . Do tiếp tuyến song song với đường thẳng y = 2 − x + 7 nên y = 2 − 0 ( 0 x ) 0 ( 0 x )
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 35 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 2 − x = 0  y = 1 − 2 0 0  = 2
−  x − 2x = 0   2 0 0 (x −1) x = 2  y = 3  0 0 0 Với x = 0, y = 1 − , y = 2
− . Phương trình tiếp tuyến cần lập: y = 2 − x −1 (nhận). 0 0 ( 0 x )
Với x = 2, y = 3, y = 2
− . Phương trình tiếp tuyến cần lập: y = 2 − x + 7 (loại). 0 0 ( 0 x ) x +1
Vậy có 1 tiếp tuyến của đồ thị hàm số y = y = − + .
x − song song với đường thẳng 2x 7 1
Slowrock321@gmail.com
Câu 59: Hàm số nào dưới đây là hàm số lẻ? A. 2
y = x − 4 − x + 4 .
B. y = 3 − x + 3 + x . C. y = x .
D. y = x − 5x +1 . Lời giải
Tác giả: Đỗ Minh Đăng, FB: Johnson Do Chọn A.
Xét hàm số y = f ( x) = x − 4 − x + 4 + TXĐ: D = Ta có x
  D  −x D .
+ f (−x) = −x − 4 − −x + 4 = − ( x − 4 − x + 4 ) = − f ( x) với x   D
Vậy hàm số y = f ( x) = x − 4 − x + 4 là hàm số lẻ.
Câu 60: Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng trung trực của đoạn AB với A(1, 3 − , 2), B( 1 − ,5, 4)
A. x − 4 y − z + 7 = 0 .
B. x − 4 y − z − 7 = 0 . C. x − 4 y − z −18 = 0 . D. x − 4 y − z +18 = 0 . Lời giải Chọn A.
Gọi I là trung điểm AB  I (0,1,3) , AB = ( 2 − ,8, 2) = 2 − (1, 4 − , − ) 1
Mặt phẳng trung trực (P) của đoạn AB qua I và vuông góc AB nên có VTPT n = (1, 4 − , − ) 1 .
Phương trình (P) : x − 4( y − )
1 − ( z − 3) = 0  x − 4 y − z + 7 = 0 .
diephd02@gmail.com 1
Câu 61: Cho tích phân ( − 2) x x
e dx = a + be  , với ;
a b . Tổng a + b bằng 0 A. 1. B. −3 . C. 5 . D. 1 − . Lời giải
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 36 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Họ và tên: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn A Đặt
u = x − 2 du = 1 1 dx 1 1   x e d x e e d e e a be x
 ( − 2) x x = ( − 2) x −
x x= − + 2 − x = 3 − 2e = + x  0  dv = e dx v = 0 e 0 0 với ;
a b  a = 3,b = −2  a + b = 1 x +1
Câu 62: Có bao nhiêu tiếp tuyến với đồ thị hàm số y = x − , biết tiếp tuyến đó song song với đường 1 thẳng y = 2 − x + 7 ? A. 2 . B. 0 . C. 1. D. 3 . Lời giải
Họ và tên: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn C. x +1 2 − y =  y = . 2 x −1 (x −1) x +1
Phương trình tiếp tuyến tại điểm M (x ; y ) của đồ thị hàm số y = 0 0 0 x − có dạng: 1
y − y = y (x − x ) . Do tiếp tuyến song song với đường thẳng y = 2 − x + 7 nên y = 2 − 0 ( 0 x ) 0 ( 0 x ) 2 − x = 0  y = 1 − 2 0 0  = 2
−  x − 2x = 0   2 0 0 (x −1) x = 2  y = 3  0 0 0 Với x = 0, y = 1 − , y = 2
− . Phương trình tiếp tuyến cần lập: y = 2 − x −1 (nhận). 0 0 ( 0 x )
Với x = 2, y = 3, y = 2
− . Phương trình tiếp tuyến cần lập: y = 2 − x + 7 (loại). 0 0 ( 0 x ) x +1
Vậy có 1 tiếp tuyến của đồ thị hàm số y = y = − + .
x − song song với đường thẳng 2x 7 1
Slowrock321@gmail.com
Câu 63: Hàm số nào dưới đây là hàm số lẻ? A. 2
y = x − 4 − x + 4 .
B. y = 3 − x + 3 + x . C. y = x .
D. y = x − 5x +1 . Lời giải
Tác giả: Đỗ Minh Đăng, FB: Johnson Do Chọn A
Xét hàm số y = f ( x) = x − 4 − x + 4
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 37 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 + TXĐ: D = Ta có x
  D  −x D .
+ f (−x) = −x − 4 − −x + 4 = − ( x − 4 − x + 4 ) = − f ( x) với x   D
Vậy hàm số y = f ( x) = x − 4 − x + 4 là hàm số lẻ.
Câu 64: Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng trung trực của đoạn AB với A(1, 3 − , 2), B( 1 − ,5, 4)
A. x − 4 y − z + 7 = 0 .
B. x − 4 y − z − 7 = 0 . C. x − 4 y − z −18 = 0 . D. x − 4 y − z +18 = 0 . Lời giải Chọn A
Gọi I là trung điểm AB  I (0,1,3) , AB = ( 2 − ,8, 2) = 2 − (1, 4 − , − ) 1
Mặt phẳng trung trực (P) của đoạn AB qua I và vuông góc AB nên có VTPT n = (1, 4 − ,− ) 1 .
Phương trình (P) : x − 4( y − )
1 − ( z − 3) = 0  x − 4 y − z + 7 = 0 .
Mar.nang@gmail.com Câu 65: Tính tổng 1 2 3 2018 S = C + C + C +...+ C bằng. 2018 2018 2018 2018 A. 2018 2 . B. 2018 2 −1. C. 2018 2 +1. D. 2019 2 −1. Lời giải
Tác giả: Lê Đình Năng, FB: Lê Năng Chọn B
Xét khai triển nhị thức Niu-tơn: (1+ x)2018 0 1 2 2 k k 2018 2018 = C + C x + C x + ... + C x + ... + C x (*). 2018 2018 2018 2018 2018
Thay x = 1 vào hai vế của (*) ta được: 2018 1 2 2018 1 2 2018 2018 2 =1+ C + C +...+ CS = C + C +...+ C = 2 −1. 2018 2018 2018 2018 2018 2018 Vậy 2018 S = 2 −1.
Câu 66: Cho tam giác ABC có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác ABC bằng A. 12 . B. 3 . C. 6 . D. 24 . Lời giải
Tác giả: Lê Đình Năng, FB: Lê Năng Chọn C
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 38 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 Theo đề 12
bài tam giác ABC có chu vi bằng 12 nên nửa chu vi là p = ; bán kính đường tròn 2
nội tiếp bằng 1, tức là ta có: r = 1.
Diện tích tam giác ABC là: S = . p r = 6.1 = 6 .
Maisonltt@gmail.com 2
Câu 67: Tính tích phân I = (2x + 1)dx  0 A. I = 5 . B. I = 6 . C. I = 2 . D. I = 4 . Lời giải
Tác giả: Nguyễn Thi Mai, FB: Mai Nguyễn Chọn B 2 2
Ta có I = (2x + 1)dx = 
( 2x + x) = 4+ 2 = 6. 0 0
Maisonltt@gmail.com
Câu 68: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = 4x − x và trục Ox 34 31 32 A. 11. B. . C. . D. . 3 3 3 Lời giải
Tác giả:Nguyễn Thị Mai, FB: Mai Nguyễn Chọn D 2
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 4x − x và trục Ox . x = 0 Xét phương trình 2
4x − x = 0   . x = 4 4 4 4 3 x 32 2 2 2 Ta có S = 4x − x dx =
(4x − x )dx = (2x − ) =   . 3 3 0 0 0
tanbaobg@gmail.com
Câu 69: Cho các số phức z thỏa mãn z = 2 5 . Biết rằng trong mặt phẳng tọa độ các điểm biểu diễn
của số phức w = i + (2 − i) z cùng thuộc một đường tròn cố định. Tính bán kính r của đường tròn đó? A. r = 5 . B. r = 10 . C. r = 20 . D. r = 2 5 . Lời giải
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 39 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Tác giả:Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo Chọn B
Ta có w = i + (2 − i) z w − i = (2 − i) z . Suy ra w − i = (2 − i) z = 2 − i . z = 10 .
Vậy tập hợp điểm biểu diễn của số phức w trên mặt phẳng tọa độ nằm trên đường tròn có bán kính r = 10 .
Câu 70: Phủ định của mệnh đề “ 2 x
  : x  0 ” là mệnh đề nào sau đây? A. 2 x   : x  0 . B. 2 x   : x  0 . C. 2 x   : x  0 . D. 2 x   : x  0 . Lời giải
Tác giả: Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo Chọn D Ta sử dụng kết quả:
Mệnh đề phủ định của mệnh đề “ x
  D : P (x) ” là mệnh đề “ x
  : P(x) ”.
hakhanhhuyen229@gmail.com
Câu 71: Trong mặt phẳng với hệ tọa độ Oxy , nếu phép tịnh tiến theo vectơ v biến điểm ( A 1; 2) thành
điểm B(1; −6) thì nó biến đường thẳng d : 2x − y + 3 = 0 thành đường thẳng d 'có phương trình
A. 2x − y − 3 = 0 .
B. 2x − y = 0 .
C. 2x − y − 8 = 0 .
D. 2x − y − 5 = 0 . Lời giải
Tác giả:Hà Khánh Huyền, FB: Hà Khánh Huyền Chọn D T ( )
A = B AB = v  (0; 8
− ) = v hay v = (0; 8 − ) . vx ' = x
Biểu thức tọa độ của phép tịnh tiến T  . vy ' = y −8 Lấy điểm M ( ;
x y)  d thì 2x − y + 3 = 0 (*) .
Gọi T (M ) = M '(x '; y ') . Lại có T (d ) = d ' nên M ' d ' . v vx ' = xx = x ' Từ   
. Thay vào (*) ta có: 2x '− ( y '+ 8) + 3 = 0  2x '− y '− 5 = 0. y ' = y −8 y = y '+ 8
Vậy phương trình của đường thẳng d ' là 2x − y − 5 = 0 .
Câu 72: Cho hàm số y = f (x) có tập xác định là \  
1 và liên tục trên mỗi khoảng xác định của nó.
Biết f (x) có bảng biến thiên như sau
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 40 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Số nghiệm của phương trình f (x) = 6 là A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Tác giả: Hà Khánh Huyền, FB: Hà Khánh Huyền Chọn C x = 2
Dựa vào bảng biến thiên f (x) = 6  x = a (a 1)
Vậy phương trình f (x) = 6 có 2 nghiệm.
maisonltt@gmail.com
Câu 73: Xét trong không gian, mệnh đề nào dưới đây là đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì vuông góc với nhau. Lời giải
Họ và tên tác giả: Nguyễn Thị Mai. Tên FB: Mai Nguyễn Chọn B
maisonltt@gmail.com
Câu 74: Phép quay góc 0
90 biến đường thẳng d thành đường thẳng d ' . Khi đó
A. d ' song song với d . B. d ' trùng d .
C. d ' tạo với d góc 0
60 D. d ' vuông góc với d . Lời giải
Họ và tên tác giả: Nguyễn Thị Mai. Tên FB: Mai Nguyễn Chọn D
bichngock36@gmail.com
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 41 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Câu 75: Trong mặt phẳng tọa độ điểm biểu diễn số phức z thỏa mãn z −1− 2i = 3 là
A. đường tròn tâm I (1; 2) , bán kính R = 9 .
B. đường tròn tâm I (1; 2) , bán kính R = 3 .
C. đường tròn tâm I (−1; −2) , bán kính R = 3 . D. đường thẳng có phương trình x + 2 y − 3 = 0 . Lời giải
Tác giả: Nguyễn Mạnh Dũng, FB: dungmanhnguyen Chọn C
Giả sử điểm M(x; y) là điểm biểu diễn số phức z . Ta có: 2 2
z −1− 2i = 3  (x −1) + ( y − 2) i = 3  (x −1) + ( y − 2) = 9 Vậy điểm M(x; y) 2 2
thuộc đường tròn (x −1) + ( y − 2) = 9 có tâm I (1; 2) , bán kính R = 3 . 8  1 
Câu 76: Trong khai triển của biểu thức 2 − 2x .   Hệ số của 7 x là:  xA. 112 . B. 112 − . C. 1792 − . D. 1792 . Lời giải
Tác giả: Nguyễn Mạnh Dũng, FB: dungmanhnguyen Chọn C 8 k  1    k 1 − − − − − − Ta có: 2 2 8 k k 8 k k 16 2k k 8 k 16 3 − 2 = . .( 2 − ) = .( 2 − ) . . = .( 2 − ) . k x C x C x x C x   8   8 8  x   x
Yêu cầu bài toán 16 − 3k = 7  k = 3 Với −
k = 3thì hệ số của 7 x là: 3 8 3 C .( 2 − ) = 1 − 792 8
tcdung.math@gmail.com
Câu 77: Để lấy nước tưới cây, ông Tráng cần xây một bể chứa nước có dạng hình hộp chữ nhật không
có nắp đậy. Nếu bể cần có thể tích 3
50m và chiều dài gấp 4 lần chiều rộng thì chiều cao bằng
bao nhiêu để chi phí vật liệu thấp nhất. A. 4, 5m . B. 5m. C. 2, 5m . D. 2m Lời giải
Tác giả: Trần Công Dũng, FB: trancong.dung.948 Chọn C 50 25
Gọi chiều rộng của bể là x (m) , x  0 . Khi đó chiều dài 4x(m) và chiều cao = (m). 2 4x 2x 25 250
Diện tích các mặt cần xây: S ( x) 2
= 4x + 2(x + 4x) 2 . = 4x + ( 2 m . 2 ) 2x 2x
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 42 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
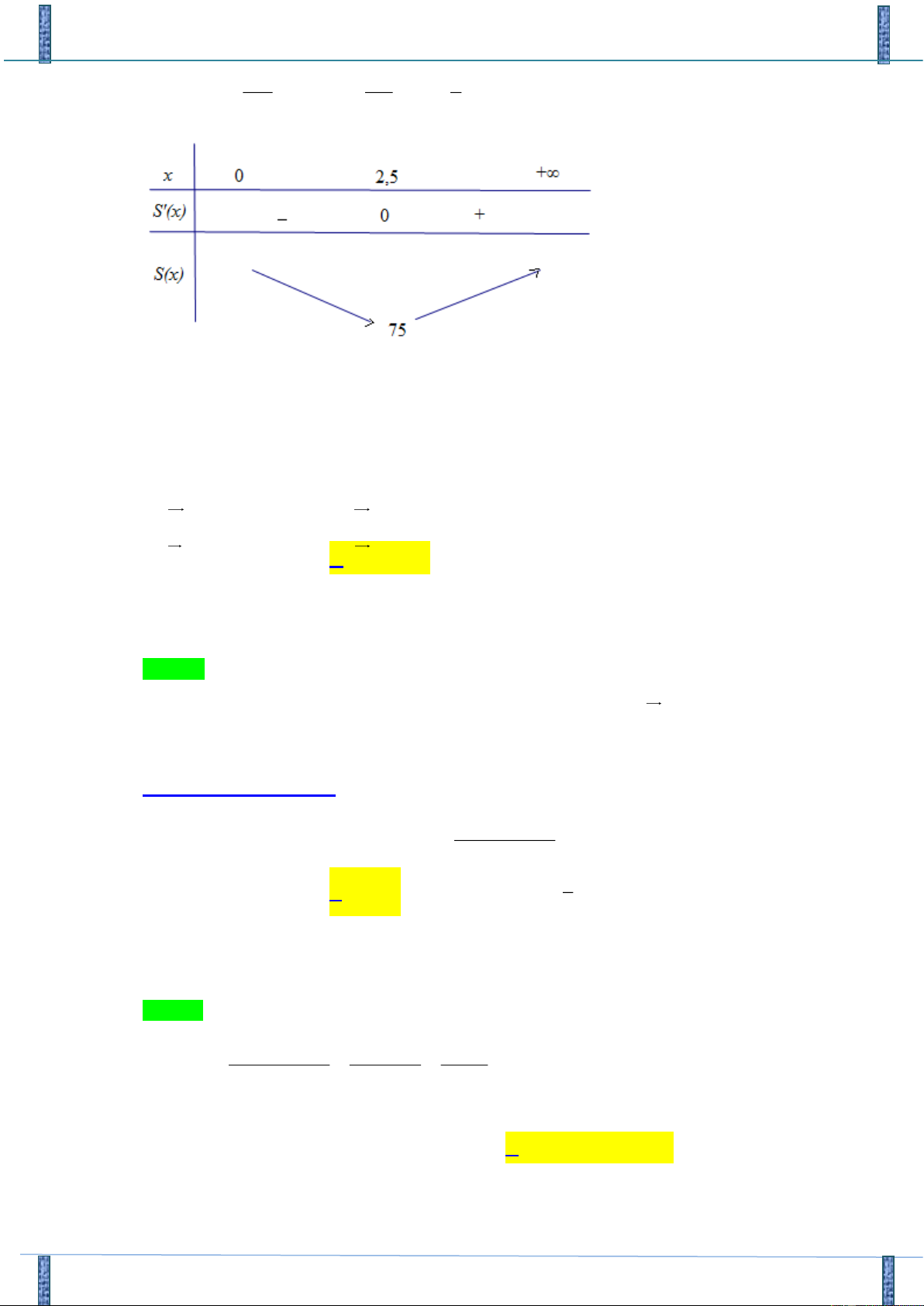
Đề KT Năng Lực GV Bắc Giang 2018-2019 250 125 5 / S ( x) 3 = 8x − = 0  x =  x = . 2 2x 8 2
Chi phí thấp nhất khi S ( x) đạt giá trị nhỏ nhất trên (0; +) . Do đó x = 2,5(m) .
tcdung.math@gmail.com
Câu 78: Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d : 2x − 3y + 4 = 0 . Vectơ nào sau đây là
một vectơ chỉ phương của d. A. u = 3; 2 − . B. u = 2;3 . 2 ( ) 4 ( ) C. u = 2; 3 − . D. u = 3; 2 3 ( ) 1 ( ) Lời giải
Tác giả: Trần Công Dũng, FB: trancong.dung.948 Chọn D
Ta thấy đường thẳng d có một vectơ pháp tuyến là (2; −3) . Do đó u = 3; 2 là một vectơ chỉ 3 ( ) phương của d.
Leminh0310@gmail.com 2sin a − cos a
Câu 79: Cho tan a = 2 . Tính giá trị biểu thức P = sina + . cos a 5 A. P = 2 . B. P = 1 . C. P = . D. P = 1 − . 3
Tác giả: Lê Hồ Quang Minh, FB: Lê Minh Lời giải Chọn B 2sin a − cos a 2 tan a −1 2.2 −1 Ta có: P = = = =1 sin a + cos a tan a +1 2 + . 1
Câu 80: Khẳng định nào sau đây là sai? A. sin ( 
− ) = −sin . B. cot ( 
− ) = −cot . C. cos( 
− ) = −cos . D. tan (  − ) = − tan .
Tác giả: Lê Hồ Quang Minh, FB: Lê Minh Lời giải
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 43 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019 Chọn C
Dễ thấy C sai vì cos (  − ) = cos .
Email: ngonguyenanhvu@gmail.com
Câu 81: Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d : x − 4y + 15 = 0 và điểm A (2; 0) .
Tìm tọa độ điểm M thuộc d để đoạn AM có độ dài nhỏ nhất. A. M ( 1 − 5;0) . B. M (5; 5) . C. M (0; 3) . D. M (1; 4) . Lời giải
Tác giả: Ngô Nguyễn Anh Vũ, FB: Euro Vu Chọn D
Điểm M d M (4t −15;t) 2 2  
Ta có: AM = ( t − ) 2 + t = ( 2 4 17
17 t − 8t + 17) = 17 (t − 4) +1  17   , t   .
 min AM = 17 , đạt được tại t = 4 . Khi đó M (1;4) .
Câu 82: Thể tích khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là 3 a 3 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 12 4 12 4 Lời giải
Tác giả: Ngô Nguyễn Anh Vũ, FB: Euro Vu Chọn B
Hình lăng trụ tam giác đều là hình lăng trụ đứng có đáy là tam giác đều 2 3  a 3 a 3 V =AA'.S = . a = .
ABC A' B'C' ABC 4 4
Thuylinh133c3@gmail.com
Câu 83: Cho tứ diện đều ABCD có độ dài cạnh bằng a . Tính tích vô hướng của hai vectơ AB và CD . 2 a A. A . B CD = 0 . B. 2 A . B CD = a . C. A . B CD = . D. 2 A . B CD =− a . 2 Lời giải
Tác giả: Nguyễn Thùy Linh, FB: Nguyễn Thùy Linh Chọn A
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 44 Mã đề 388
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề KT Năng Lực GV Bắc Giang 2018-2019
Gọi M là trung điểm của DC .
Do ABCD là tứ diện đều nên ta có: DC ⊥ AM
DC ⊥ ( AMB)  DC ⊥ AB A . B CD = 0. DC ⊥ BM
Thuylinh133c3@gmail.com
Câu 84: Một hộp đựng 9 quả cầu được đánh số lần lượt từ 1 đến 9. Lấy ngẫu nhiên một quả cầu từ hộp
đó. Tính xác suất lấy được quả cầu mang số chẵn. 2 5 4 4 A. . B. . C. . D. . 3 9 5 9 Lời giải
Tác giả: Nguyễn Thùy Linh, FB: Nguyễn Thùy Linh Chọn D
Xét phép thử: “Lấy ngẫu nhiên một quả cầu từ hộp đựng 9 quả cầu” Ta có: n () 1 = C = 9. 9
Gọi A là biến cố: “ Lấy được quả cầu mang số chẵn "
n( A) =  P( A) n( A) 4 4 = = n () . 9
Chia sẻ bởi Nguyễn Văn Quý Admin Group FB: STRONG TEAM TOÁN VD-VDC.
Trang 45 Mã đề 388
Document Outline

  • Đề-GV-Bắc-Giang-2018-2019
  • [STRONG TEAM TOÁN VD-VDC]-Đề-GV-Bắc-Giang-2018-2019-2