lOMoARcPSD|45315597
Kiểm tra điều kiện
Môn: Xác suất – Thống kê Thời gian: 60 phút
Câu 1. Cho A, B là hai biến cố của một phép thử ngẫu nhiên nào đó. Biết rằng P ( A) ý 0, 4 , P ( B) ý 0, 5 và P ( A  B) ý 0, 65 . Giá trị của
P ( AB) bằng A. 0,4. B. 0,25. C. 0,2. D. 0,5.
Câu 2. Một lô hàng gồm 80 sản phẩm loại I và 40 sản phẩm loại II. Xác suất để khi lấy ngẫu nhiên một sản phẩm từ lô hàng ta
được sản phẩm loại II là A. 1 . B. 1 . C. 2 . D. 2 . 2 3 3 5
Câu 3. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất là f ( x) với mọi x þ . Khẳng định nào dưới đây là sai? 2  2
A. P ( X ü 2) ý  f (x )dx .
B. f ( x)  0 , với mọi x þ .
C.  f (x )dx ý 1. D. P ( X ü 2) ý  f (x )dx .   0
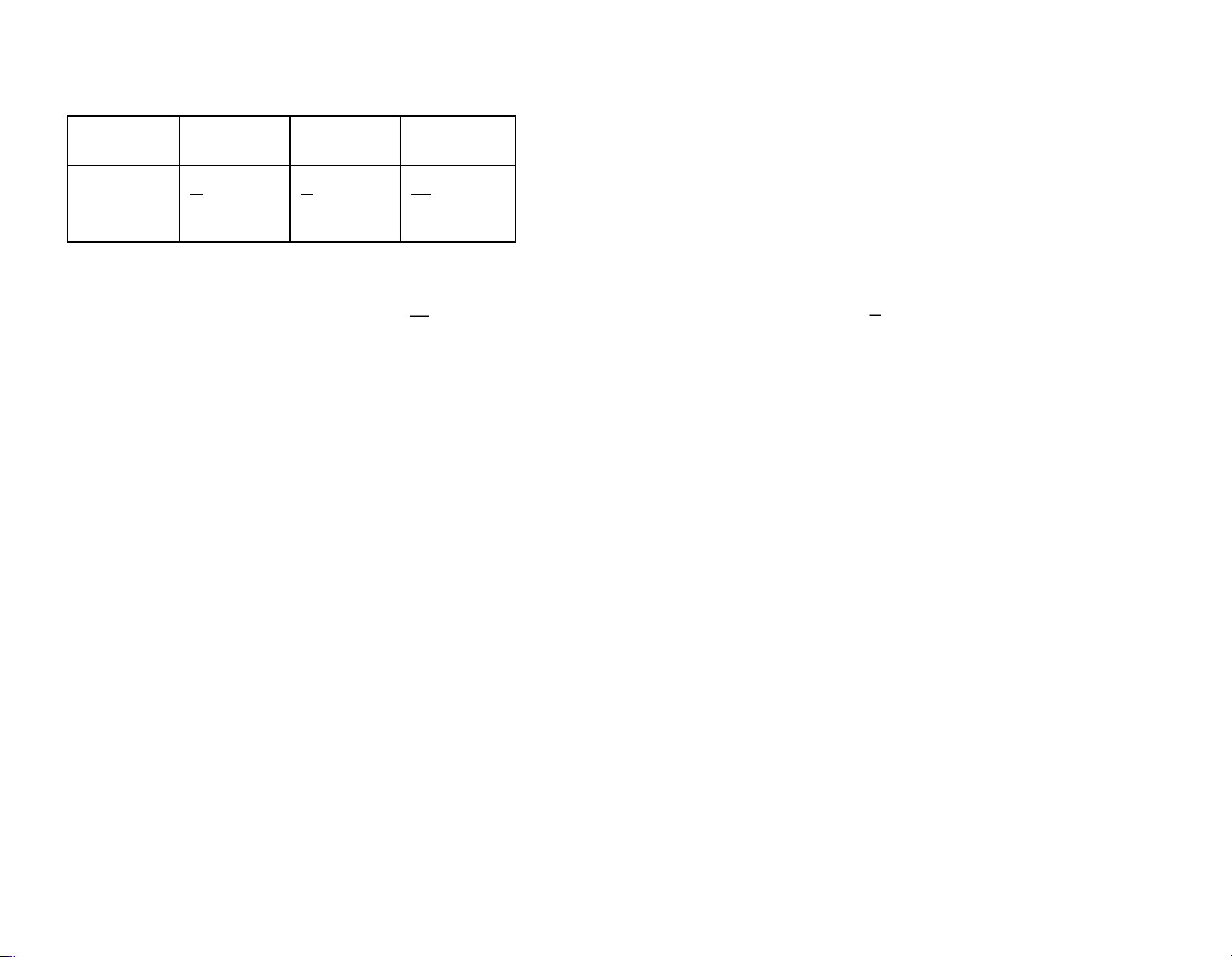
Câu 4. Cho X là biến ngẫu nhiên có bảng phân phối xác suất x 1 2 3 4 p 0,3 0,2 0,4 0,1
Xác suất để X ý 2, 5 là
A. P(X ý 2,5) ý 0,2.
B. P(X ý 2,5) ý 0,5 .
C. P(X ý 2,5) ý 0,3 .
D. P(X ý 2,5) ý 0.
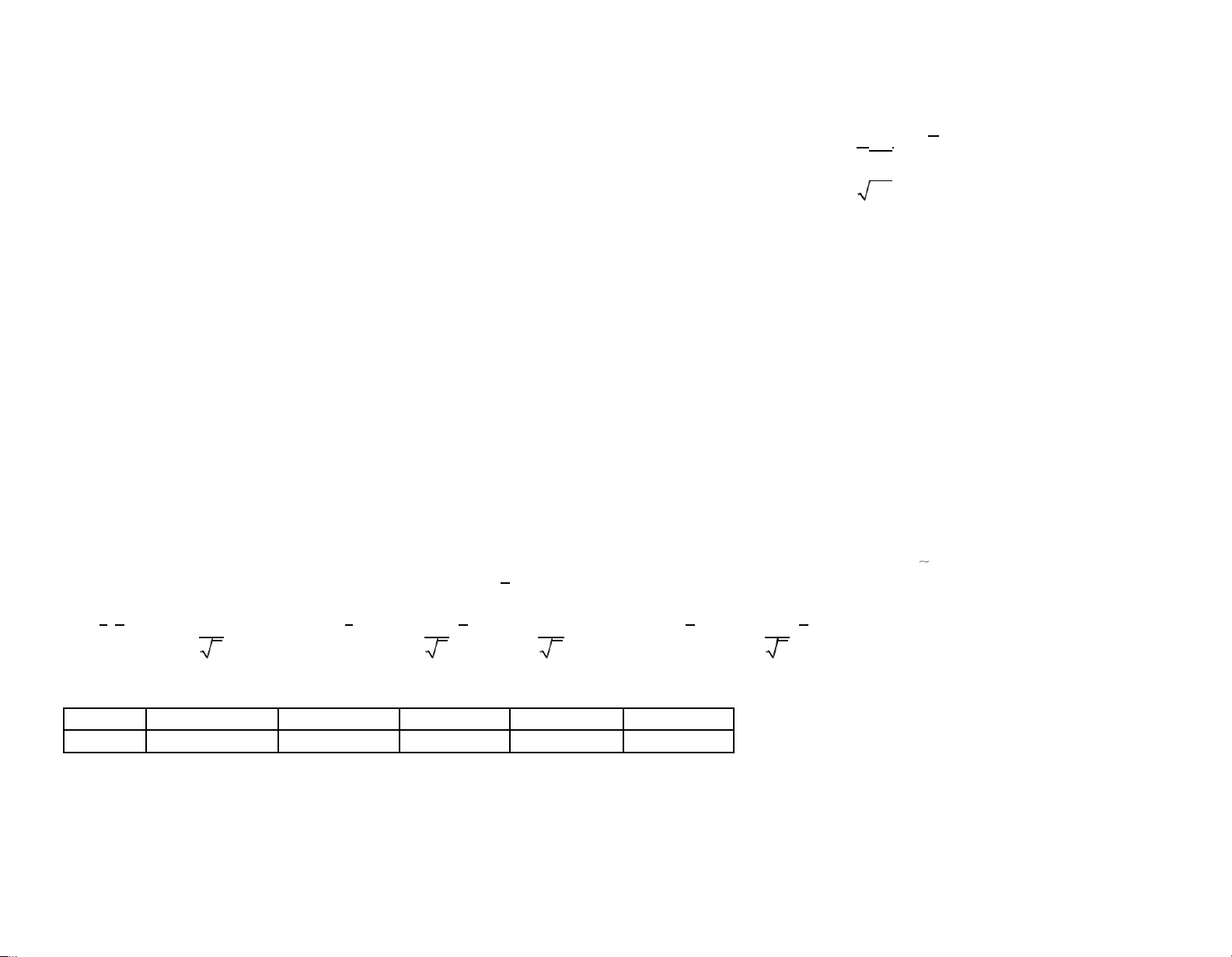
Câu 5. Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất lOMoARcPSD|45315597 x -2 1,5 4 p 1 1 7 4 6 12
mod ø X ù nhận giá trị nào trong các giá trị sau?
D. mod ø X ù ý 1 .
A. mod ø X ù ý 4 .
B. mod ø X ù ý 7 . C. mod ø X ù ý 2 . 12 4
Câu 6. Đo chỉ số K trong chất lỏng ở khu A (đơn vị: ppm) của 7 mẫu thử từ các địa điểm khác nhau ta thu được 182, 187, 174,
252, 280, 197, 158. Tính kỳ vọng của mẫu đã cho (Kết quả làm tròn đến số thập phân thứ nhất). A. 204,3. B. 46,6. C. 204,1. D. 43,3.
Câu 7. Xét nghiệm ngẫu nhiên 500 người trong khu vực A để đánh giá về sự truyền nhiễm b ệnh V. Các chuyên gia nhận được 20% s ố ca có
kết quả nghi ngờ và 25% các ca nghi ngờ có kết quả chính xác là nhiễm bệnh V. Tỷ lệ phần trăm số người nhiễm bệnh V trong mẫu đã cho là A. 5%. B. 0.5%. C. 10%. D. 15%.
Câu 8. Trọng lượng sản phẩm do nhà máy sản xuất ra là một biến ngẫu nhiên có phân phối chuẩn N (  ,  2 ) với trọng lượng trung bình theo
quy định là 50 kg. Nghi ngờ máy hoạt động không bình thường làm thay đổi trọng lượng trung bình của sản phẩm, người ta cân thử một
số sản phẩm và thu được trọng lượng trung bình là 50,5 kg. Giả thuyết H 0 và đối thuyết H1 được đạt ra trong bài toán kiểm định này là
A. Giả thuyết H0 :  ý 50 và đối thuyết H1 :   50 .
B. Giả thuyết H0 :  ý 50 và đối thuyết H1 :  þ 50 .
C. Giả thuyết H0 :  ý 50, 5 và đối thuyết H1 :  þ 50, 5 .
D. Giả thuyết H0 :  ý 50, 5 và đối thuyết H1 :   50, 5 .
Câu 9. Tỷ lệ khách hàng tiêu dùng một loại sản phẩm A ở thành phố B không vượt quá 55%. Các nhà phân phối sản phẩm A muốn tăng tỷ lOMoARcPSD|45315597 x 1 t 2  
lệ này lên. Họ đã thực hiện chiến dịch quảng cáo mới liên quan đến sản phẩm này. Biết rằng  ( x ) ý e d
2 t với mọi số thực x , 2 
 (1, 96) ý 0, 975 và  (1, 645) ý 0, 95 . Với mức ý nghĩa 5%, miền bác bỏ W trong bài toán kiểm định tính hiệu quả của quảng cáo mới là
A. W ý (1,96; ) .
B. W ý (1,96; ) .
C. W ý (1, 645; ) .
D. W ý (1, 645; ) .
Câu 10. Xác suất thi qua môn Toán cao cấp của một sinh viên ở lần 1 và lần 2 lần lượt là 0,4 và 0,8. Biết rằng mỗi sinh viên được
thi tối đa 2 lần. Hỏi xác suất để sinh viên thi qua môn Toán cao cấp là bao nhiêu? A. 0,6. B. 0,4. C. 0,32. D. 0,88.
Câu 11. Một lớp học có 30 sinh viên đăng kí thi môn Toán T. Biết rằng tỷ lệ thi qua môn là 45%. Xác suất để có đúng một nửa số
sinh viên của lớp thi qua môn Toán T là A. 0,124. B. 0,45. C. 0,225. D. 0,876.
N (  ,  2 ) (với 
Câu 12. Công thức ước lượng khoảng tin cậy đối xứng (với độ tin cậy 1  ñ ) cho kỳ vọng của biến ngẫu nhiên X đã
biết ; mẫu quan sát có cỡ n và giá trị của kỳ vọng mẫu là x ; uò là phân vị chuẩn mức ò ) là ö  ö ö   ö ö  ö
A. ÷ x; x  u1(ñ / 2)  ÷ .
B. ÷ x  u1 (ñ / 2) .
; x  u1( ñ / 2) . ÷.
C. ÷ x  u1( ñ / 2) . ; x ÷ . D. ( ; ). ø n ø ø n n ø ø n ø
Câu 13. Cho biến ngẫu nhiên X có bảng phân phối xác suất X 1 2 3 4 5 p 0,2 0,1 0,2 0,1 0,4
Gọi F ( x) là hàm phân phối xác suất của X . Giá trị của F (3, 5) là A. 0,6. B. 0,2. C. 0,3. D. 0,5. lOMoARcPSD|45315597
Câu 14. Cho biến ngẫu nhiên liên tục X
có hàm mật độ xác suất là ÿ  
ük . x2 khi x þ 0; 2
f ø x ù ý ý
(với k là tham số). ÿ0 khi x ÿ 0; 2 þ
Giá trị của k bằng: A. k ý 8 . B. k ý 3 . C. k ý 1 . D. k ý 1 . 3 8 8 4
Câu 15. Trọng lượng (đơn vị: kg) của mỗi sản phẩm do nhà máy T sản xuất là một biến ngẫu nhiên X có phân phối chuẩn. Cân ngẫu nhiên 25
sản phẩm, người ta thu được trọng lượng trung bình bằng 4,5 kg và phương sai mẫu hiệu chỉnh bằng 0,2025 kg2. Biết rằng Tò( k ) là phân vị
Student với k bậc tự do và mức xác suất bằng ò , T (24) (24) 0,95
ý 2, 711 và T0,975
ý 2, 064 . Với độ tin cậy 95%, khoảng tin cậy đối xứng cho trọng
lượng trung bình của sản phẩm là A. (4,42062; 4,57938). B. (4,3236; 4,6764). C. (4,31424; 4,68576). D. (4,416408; 4,583592).
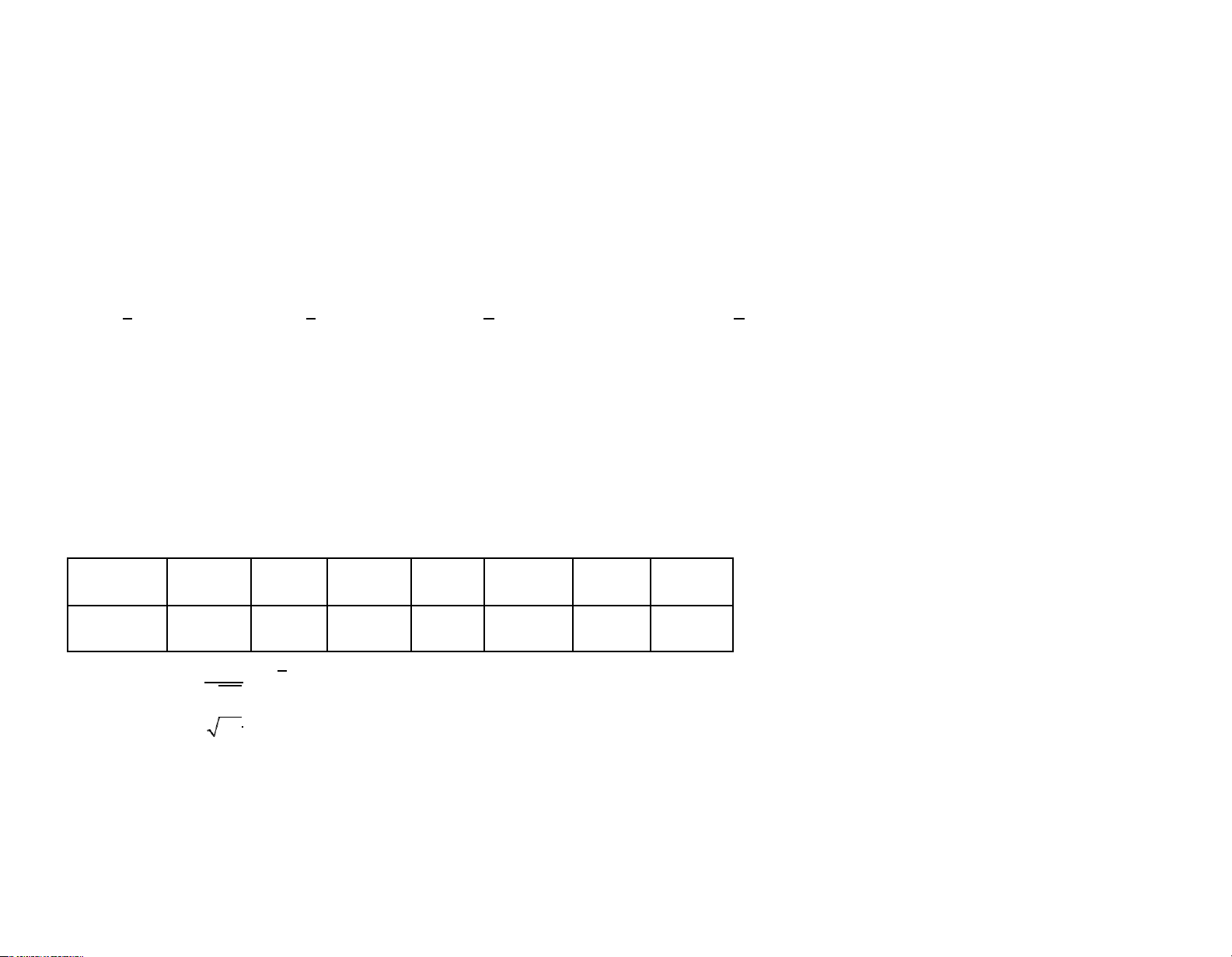
Câu 16. Đo ngẫu nhiên chiều cao (đơn vị: mét) của 100 cây keo trồng được một năm tuổi, người nghiên cứu thu được bảng số liệu sau: Chiều cao 1,62 1,65 1,74 1,82 1,95 2,0 2,15 Số cây 5 10 10 30 20 20 5 x t 2 1  
Biết rằng  ( x )
 (1, 96) ý 0, 975 ,  (1, 645) ý 0, 95 và một cây được một năm tuổi được gọi là ý e
2 dt với mọi số thực x , đạt 2 
chuẩn nếu chiều cao của nó lớn hơn 1,8 mét. Với độ tin cậy 95%, khoảng tin cậy đối xứng cho tỷ lệ cây được một năm tuổi đạt chuẩn là A. (0,75; 0,83487). B. (0,71325; 0,78675). C. (0,66513; 0,83487). D. (0,66513; 0,75). lOMoARcPSD|45315597
Câu 17. Một trang trại nuôi gà tuyên bố rằng tỷ lệ gà có trọng lượng trên 2,5 kg là 95%. Nhiều người mua gà của trang trại nghi
ngờ rằng rằng tỷ lệ này phải thấp hơn. Họ đã cân ngẫu nhiên một số lượng lớn các con gà và thu được tỷ lệ gà có trọng lượng trên 2,5 kg là 93%. x t 2
Biết rằng  ( x ) 1 ý
 e  2 dt với mọi số thực x ,  (2, 326) ý 0, 99 và  (2, 576) ý 0, 995 . Gọi p là tỷ lệ gà có trọng lượng trên 2,5 kg của 2 
trang trại. Với mức ý nghĩa 1%, giả thuyết H 0 , đối thuyết H1 và miền bác bỏ W để tiến hành kiểm định là H
A. ýü : p ý 0, 95 0
và W ý ( ; 2, 326) .
B. ýüH 0 : p ý 0, 93 và W ý ( ; 2, 326) .
þH 1 : p ü 0, 95
þH 1 : p ü 0, 93 H H
C. ýü : p ý 0, 95 : p ý 0, 93 0
và W ý ( ; 2, 576)(2,576; ) . D. ýü 0
và W ý ( ; 2, 576) (2, 576; ) .
þH 1 : p  0,
þH 1 : p  0, 95 93
Câu 18. Trọng lượng sản phẩm A do nhà máy T sản xuất là một đại lượng ngẫu nhiên X có quy luật phân phối chuẩn N (  , 
2 ) . Nhà máy tuyên bố rằng trọng lượng trung bình của sản phẩm là 1,45 kg. Một người mua hàng nghi ngờ rằng trọng lượng
trung bình của sản phẩm thấp hơn mức công bố. Người đó đã cân ngẫu nhiên 100 sản phẩm và thu được trọng lượng trung bình
mỗi sản phẩm trong mẫu là 1,43 x 1 t 2  
kg, độ lệch mẫu hiệu chỉnh là 0,3 kg. Biết rằng  ( x ) e ý
2 dt với mọi số thực x ,  (1, 96) ý 0, 975 ,  (1, 645) ý 0, 95 . Với mức ý 2 
nghĩa 5%, giá trị tiêu chuẩn kiểm định Z (Kết quả làm tròn đến chữ số thập phân thứ tư) và miền bác bỏ W để tiến hành kiểm định là (1, 96;
A. Z ý 0, 6667 và W= ( ; 1, 645) .
B. Z ý 0, 6667 và W= ( ; 1, 96) ) . (1, 96;
C. Z ý 0, 6667 và W= ( ; 1, 645) .
D. Z ý 0, 6667 và W= ( ; 1, 96) ) .
Câu 19. Thời gian hoàn thành của một chi tiết máy do nhà máy T sản xuất là một đại lượng ngẫu nhiên có quy luật phân phối chuẩn N (
 ,  2 ) với thời gian hoàn thành trung bình là 30 phút. Nhà máy muốn giảm bớt thời gian hoàn thành của một chi tiết máy nên đã áp
dụng phương pháp sản xuất mới. Sau một thời gian áp dụng, nhà máy đã kiểm tra ngẫu nhiên 20 chi tiết máy và thu được thời gian hoàn
thành trung bình là 28,35 phút và độ lệch mẫu hiệu chỉnh là 1,5 phút. Biết rằng T (
ò k ) là phân vị Student với k bậc tự do và mức xác suất lOMoARcPSD|45315597
bằng ò , T (19) (19) 0,95
ý 1, 729 và T0,975
ý 2, 093. Với mức ý nghĩa 5%, giá trị tiêu chuẩn kiểm định Z (Kết quả làm tròn đến chữ số
thập phân thứ tư) và miền bác bỏ W để tiến hành kiểm định là
A. Z ý 4, 9193 và W= ( ; 2, 093) .
B. Z ý 4, 9193 và W= ( ; 1, 729) .
C. Z ý 4, 9193 và W= ( ; 2, 093) .
D. Z ý 4, 9193 và W= ( ; 1, 729) .
Câu 20. Trọng lượng mỗi chi tiết máy B do nhà sản xuất M sản xuất là đại lượng ngẫu nhiên X tuân theo phân phối chuẩn N (  ,  2 ) với độ
lệch chuẩn là  ý 1, 2 gam. Nhà máy tuyên bố rằng trọng lượng trung bình của chi tiết máy là 15 gam. Người ta nghi ngờ con số này phải cao
hơn mức công bố. Người đó đã điều tra ngẫu nhiên 90 chi tiết máy và thu được trọng lượng trung bình là 15,2 gam. Giả thuyết H 0 ,
đối thuyết H1 và giá trị tiêu chuẩn kiểm định Z (Kết quả làm tròn đến chữ số thập phân thứ ba) được xác định theo phương án nào trong các phương án sau? H A. ýü :
0  ý15 và Z ý 1, 581 .
B. ýüH0 :  ý15,2 và Z ý 1, 581 . H
þH1 :  þ 1 : þ15 þ15,2 H H C. ýü :
0 : ý15 và Z ý 1, 581 .
D. ýü 0  ý15,2 và Z ý 1, 581
þH1 : 
þH1 :  þ15 þ15,2
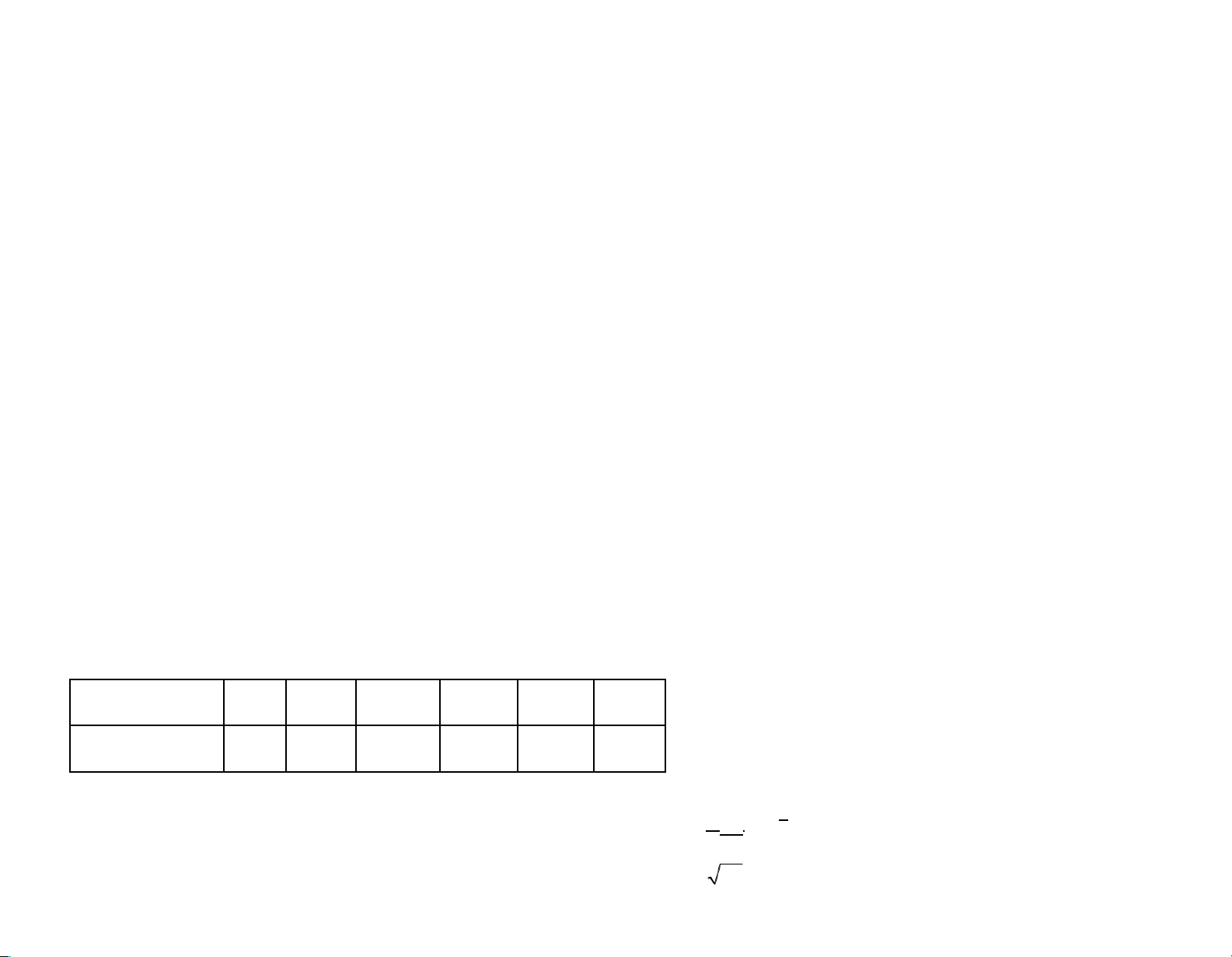
Câu 21. Cân ngẫu nhiên 400 sản phẩm được sản xuất bởi nhà máy H và thu được bảng số liệu sau: Trọng lượng (kg) 1 1,2 1,4 1,6 1,8 2 Số sản phẩm 22 66 160 120 22 10
Biết rằng trọng lượng của mỗi sản phẩm được sản xuất bởi nhà máy H là một biến ngẫu nhiên có phân phối chuẩn với kỳ vọng là EX và x 1 t 2  
 (1, 96) ý 0, 975 ,  (1, 645) ý 0, 95 ,  (2, 326) ý 0, 99 ,  (2, 576) ý 0, 995 (với  (
dt x ). Với độ tin cậy 99%, khoảng x ) ý e 2 ước 2  lOMoARcPSD|45315597
lượng đối xứng cho trọng lượng trung bình của mỗi sản phẩm là A. 1,442 < EX < 1,4689. B. 1,4364 < EX < 1,442. C. 1,4364 < EX < 1,4476. D. 1,4151 < EX < 1,4689.
Câu 22. Để ước lượng số lượng của loài sinh vật A trong khu vực X , người ta tiến hành như sau: Đầu tiên, họ thả thêm 500 con sinh
vật A có đánh dấu vào khu vực này. Sau đó, bắt ngẫu nhiên 400 con sinh vật A từ khu vực này và thấy có 50 con sinh vật A có đánh
dấu. Cuối cùng, họ sử dụng khoảng tin cậy đối xứng cho tỷ lệ sinh vật A có đánh dấu trong khu vực để ước lượng được số lượng sinh
vật A ban đầu x 1 t 2 
trong khu vực nằm trong khoảng nào. Biết rằng  ( x ) ý
 e 2dt với mọi số thực x ,  (1, 96) ý 0, 975 ,  (1, 645) ý 0, 95 . Với độ tin 2 
cậy 95%, số lượng sinh vật A trong khu vực ban đầu (ký hiệu là N) nằm trong khoảng nào sau đây?
A. 3177 ü N ü 5400 .
B. 3177  N ü 5400 .
C. 2677  N ü 4900 .
D. 2677  N  4900 .
Câu 23. Lượng nước sạch (tính theo m3 ) của một gia đình 4 người ở thành phố H sử dụng trong 6 tháng năm ngoái là 17 m3 . Theo dõi lượng
nước sạch sử dụng trong 6 tháng năm nay của 60 gia đình 4 người, người ta thấy lượng nước sạch trung bình của các gia đình là 17,38 m3 và độ
lệch mẫu hiệu chỉnh là 1,12 m3 . Có ý kiến cho rằng lượng nước tiêu thụ năm nay tăng lên. Với mức ý nghĩa 5%, kết luận nào sau đây là đúng?
Biết rằng, lượng nước sạch tiêu thụ của các gia đình 4 người là một biến ngẫu nhiên có phân phối chuẩn, miền bác bỏ x 1 t 2 
để tiến hành kiểm được ký hiệu là W ,   ( x )
dt với mọi số thực x ,  (1, 96) ý 0, 975 ,  (1, 645) ý 0, 95 ý e 2 . 2 
A. W ý (1, 645; ) và lượng nước tiêu thụ năm nay đã tăng lên.
B. W ý ( ; 1, 96)  (1, 96; ) và lượng nước tiêu thụ năm nay đã tăng lên.
C. W ý (1, 645; ) và lượng nước tiêu thụ năm nay không tăng lên.
D. W ý ( ; 1, 96)  (1, 96; ) và lượng nước tiêu thụ năm nay không tăng lên. lOMoARcPSD|45315597
Câu 24. Độ dài một chi tiết máy là một đại lượng ngẫu nhiên X có quy luật phân phối chuẩn N (  ,  2 ) với độ dài trung bình là 10
cm. Một người mua hàng nghi ngờ rằng con số này phải thấp hơn. Anh ta đo thử 28 chi tiết máy và tính được tiêu chuẩn thống kê
là Z ý 1, 642 . Biết rằng Tò( k ) là phân vị Student với k bậc tự do và mức xác suất bằng ò , T0,95(27) ý 1, 703 và T0,975(27) ý 2, 052. Với
mức ý nghĩa 5%, lựa chọn nào là đúng?
A. Giả thuyết H 0 :  ý 10 , đối thuyết H1 :  þ 10 và thông tin về chi tiết máy là đúng.
:  ý 10 , đối
B. Giả thuyết H 0 thuyết
H1: ü10 và thông tin về chi tiết máy là sai.
:  ý 10 , đối
C. Giả thuyết H 0 thuyết
H1: 10 và thông tin về chi tiết máy là đúng.
D. Giả thuyết H 0 :  ý 10 , đối thuyết H1 :  ü 10
và thông tin về chi tiết máy là đúng.
Câu 25. Dây chuyền lắp ráp nhận được các chi tiết do 2 máy sản xuất. Trung bình máy thứ nhất cung cấp 60% chi tiết, máy thứ
hai cung cấp 40% chi tiết. Khoảng 90% chi tiết do máy thứ nhất sản xuất đạt tiêu chuẩn, còn 70% chi tiết do máy thứ hai sản
xuất đạt tiêu chuẩn. Lấy ngẫu nhiên từ dây chuyền một sản phẩm, xác suất để sản phẩm này đạt tiêu chuẩn là A. 0,8. B. 0,82. C. 0,5. D. 0,78.
Câu 26. Theo thống kê về tỉ lệ mắc bệnh A trong khu vực B, nếu một người đã tiêm vắc-xin phòng bệnh A thì tỉ lệ nhiễm bệnh là
1%. Nếu chưa tiêm vắc-xin thì tỉ lệ nhiễm bệnh là 6%. Biết trong 1000 người thì có 800 người được tiêm vắc-xin. Chọn ngẫu nhiên
một người, hỏi khả năng người này mắc bệnh A là bao nhiêu? A. 3,5%. B. 2%. C. 2,8%. D. 1,2%.
Câu 27. Xác suất để xạ thủ A bắn một viên đạn trúng đích là 0,8. Để xác suất có ít nhất một viên không trúng đích lớn hơn 0,7 thì
xạ thủ này phải bắn tối thiểu bao nhiêu viên đạn? lOMoARcPSD|45315597 A. 5 viên. B. 6 viên. C. 7 viên. D. 8 viên.
Câu 28. Một lô hàng gồm rất nhiều sản phẩm được tuyển chọn để xuất khẩu, biết rằng nó có tỉ lệ phế phẩm là 5%. Lấy ngẫu nhiên 10 sản
phẩm để kiểm tra, biết rằng xác suất để trong 10 sản phẩm lấy ra có nhiều nhất k phế phẩm là không nhỏ hơn 95%. Giá trị của k tối thiểu là A. k ý 1 . B. k ý 2 . C. k ý 3 . D. k ý 4 . x 1 t 2 
dt với mọi số thực x , e  ( 2, 3) ý 0,
Câu 29. Cho X là biến ngẫu nhiên có phân phối chuẩn N ø1; 0,12 ù . Biết rằng  ( x ) ý 2  20107
. Giá trị thực của tham số a để p  X ü a ý 0, 9893 là A. a ý 2, 3. B. a ý 1, 23 . C. a ý 0, 23 . D. a ý 1, 023 .
Câu 30. Cho X là biến ngẫu nhiên có phân phối chuẩn với kỳ vọng của X bằng 4 và độ lệch chuẩn của X bằng 0,2. Xác suất để 1 x t 2 
X  4, 32 bằng bao nhiêu? Biết rằng  ( x ) ý 2  
dt với mọi số thực x , e
 (1, 6) ý 0, 9452 và  (4, 32) ý 0, 999 . 2  A. 0,999. B. 0,0548. C. 0,9452. D. 0,001.