Đề KSCL đội tuyển HSG Toán 10 năm 2018 – 2019 trường Yên Lạc 2 – Vĩnh Phúc

SỞ GD&ĐT VĨNH PHÚC
KỲ THI KSCL ĐỘI TUYỂN HỌC SINH GIỎI KHỐI 10 TRƯỜNG THPT YÊN LẠC 2 ĐỀ THI MÔN: TOÁN NĂM HỌC 2018-2019
Thời gian làm bài: 180 phút, không kể thời gian giao đề. 1
Câu 1 (2,0 điểm). Tìm tập xác định của hàm số 2 y 
 x  7x  6 1 1 2x
Câu 2 (2,0 điểm). Cho hàm số 2
y  x  2mx  3m và hàm số y  2
 x  3. Tìm m để hai đồ
thị đã cho cắt nhau tại hai điểm phân biệt A và B sao cho AB  4 5 .
Câu 3 (2,0 điểm). Tìm m để phương trình 2
2x  2x  m  x  1 có nghiệm. x 1
Câu 4 (2,0 điểm). Tìm tham số m để bất phương trình
 1 có tập nghiệm là  . 2
mx  4x  m  3
Câu 5 (2,0 điểm). Giải phương trình 2 2x 6x 1   4x 5
 4x 10y  2x 2y  4 
Câu 6 (2,0 điểm). Giải hệ phương trình  2 2 
2 2x  7xy  5y x  2y   24  3
Câu 7 (2,0 điểm). Cho tam giác ABC đều cạnh 3a. Lấy các điểm M, N lần lượt trên các cạnh
BC, CA sao cho BM =a, CN=2a. Gọi P là điểm nằm trên cạnh AB sao cho AM vuông góc với
PN. Tính độ dài PN theo a.
Câu 8 (2,0 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có BC  2 AB , 
phương trình đường trung tuyến xuất phát từ đỉnh B là d  : x  y  2  0 . Biết 0 ABC  120 và A3; 
1 . Tìm tọa độ các đỉnh còn lại của tam giác.
Câu 9 (2,0 điểm). Cho tam giác ABC gọi I là tâm đường tròn nội tiếp A
 BC , biết IG  IC .
a  b  c 2ab Chứng minh rằng 
(Với AB  c, BC  a,CA  b ). 3 a  b 3
Câu 10 (2,0 điểm). Cho các số thực a, ,
b c  0 thỏa mãn a  b  c 
. Tìm giá trị nhỏ nhất 2 2 1 2 1 2 1 của S  a   b   c  . 2 2 2 b c a ------Hết------
Thí sinh không được sử dụng tài liệu.Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………….………..…….…….….….; Số báo danh………………… SỞ GD&ĐT VĨNH PHÚC
KỲ THI KSCL ĐỘI TUYỂN HỌC SINH GIỎI KHỐI 10
(Đáp án có 05 trang) ĐỀ THI MÔN: TOÁN NĂM HỌC 2018-2019 I. LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài học sinh làm
theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn. II. ĐÁP ÁN: Câu Nội dung trình bày Điểm 1 1
(2,0 điểm). Tìm tập xác định của hàm số 2 y 
 x  7x  6 1 1 2x 2
x 7x 6  0 
Hàm số có xác định khi và chỉ khi  0,5 1   12x  0  x 1 2
x 7x 6  0          x  6  0,5 1   12x  0    1  12x 1  x 1      x  6  0  x 1   0,5 0   x 1 
Vậy tập xác định của hàm số là: D  0  ;1 0,5 (2,0 điểm). Cho hàm số 2
y  x  2mx  3m và hàm số y  2
 x  3. Tìm m để hai 2
đồ thị đã cho cắt nhau tại hai điểm phân biệt A và B sao cho AB  4 5 .
Phương trình hoành độ giao điểm của hai đồ thị là: 2
x  2mx 3m  2  x 3 0,5 2
 x  2m  
1 x  3m  3  0 (*)
Hai đồ thị cắt nhau tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt m 1   '  0    .  0,5 m  4 
Gọi Ax ;2x  3 ; B x ;2x  3 với x ; x là nghiệm phương trình (*) 1 1   2 2  1 2 x  x  2  m 1  1 2   Theo Vi-et ta có:  x .x  3  m 1   1 2   0,5 2 2 2
Ta có: AB  5 x  x  5 x  x  20x .x 
20 m 1  60 m 1 1 2   1 2  1 2     AB   m  2  m     m  2 4 5 20 1 60 1 4 5 1  2m   1  4  0 0,5
 m  0; m  5
 . So sánh với điều kiện ta được m=0 và m=-5 3
(2,0 điểm). Tìm m để phương trình 2
2x  2x  m  x  1 có nghiệm. x  1 Ta có 2
2x  2x  m  x  1   0,5 2
x  4x  m  1  0(*)   2 (*)
x  4x  1  m . Xét y  2
x  4x và y  1  m 0,5 x 1 2 + ∞ -3 + ∞ y 0,5 -4
Ta có bảng biến thiên hàm số y  2 x  4x là:
Phương trình đã cho có nghiệm khi và chỉ khi (*) phải có nghiệm x  1 hay 0,5
1  m  4  m  5 x 1
(2,0 điểm). Tìm tham số m để bất phương trình  1 có tập 2 4
mx  4x  m  3 nghiệm là  .
Để bất phương trình có tập nghiệm  ta cần có 2
mx  4x  m  3  0 với x    m  0 m  0 m  1 0,5
( m =0 không thỏa mãn)      2    0 
m  3m  4  0 m  4   Với m  1  . Khi đó ta có 2
mx  4x  m  3  0 với x    Bpt 2 2
 x 1  mx  4x  m  3  mx  5x  m  4  0 (1)  4  41 m   2 Bpt có tập nghiệm  2  
 0  4m 16m  25  0   (1) 0,5  4  41 m   2 4  41
Mà m  1  m  2
Với m  4 . Khi đó ta có 2
mx  4x  m  3  0 với x    Bpt 2 2
 x 1  mx  4x  m  3  mx  5x  m  4  0 (2)  4  41 m   2 Bpt có tập nghiệm  2  
 0  4m 16m  25  0   0,5 ( 2)  4  41 m   2 4  41
Mà m  4  m  2 4  41 4  41 KL: m  ; m  0,5 2 2 5
(2,0 điểm). Giải phương trình 2 2x 6x 1   4x 5 4
Điều kiện: x   . 5 0,5
Đặt t  4x  5  t  0 2 t 5 Ta có x 
thay vào ta được phương trình sau: 4 0,5 4 2 t 10  t  25 6 2.   2t   4 2 5 1
  t  t 22t 8t 77  0 16 4
  2t  t   2 2 7 t  2t 1   1  0 0,5 t  1  2 2  1  t 1 2 2     t  1   2 2 x 1 2 2 t 0            0,5 t  1 2 3 t 1 2 3 x  2 3 3     t 12 3  4
 4x 10y  2x 2y  4  6
(2,0 điểm). Giải hệ phương trình  2 2 
2 2x  7xy  5y x  2y   24  3
Đặt a  4x 10 y;b  2x  2 y a,b  0
ab  4 
ab  4   0,5 Khi đó hệ trở thành 2 2 a b ab   2 2     24
a b  2ab 144   6 3
ab  4 a  8      
ab  4
a b 12  b   4      a  8  a,b 0            0,5 a  b  2 144    a b  4    a  4 b   4       
 a  b  12   b   8     a  8
 4x 10y  8   
2x  5y  32   Với      0,5 b   4       x  y  8 2x 2 y 4   8 16
Giải hệ trên ta được x  ; y  . 0,5 3 3
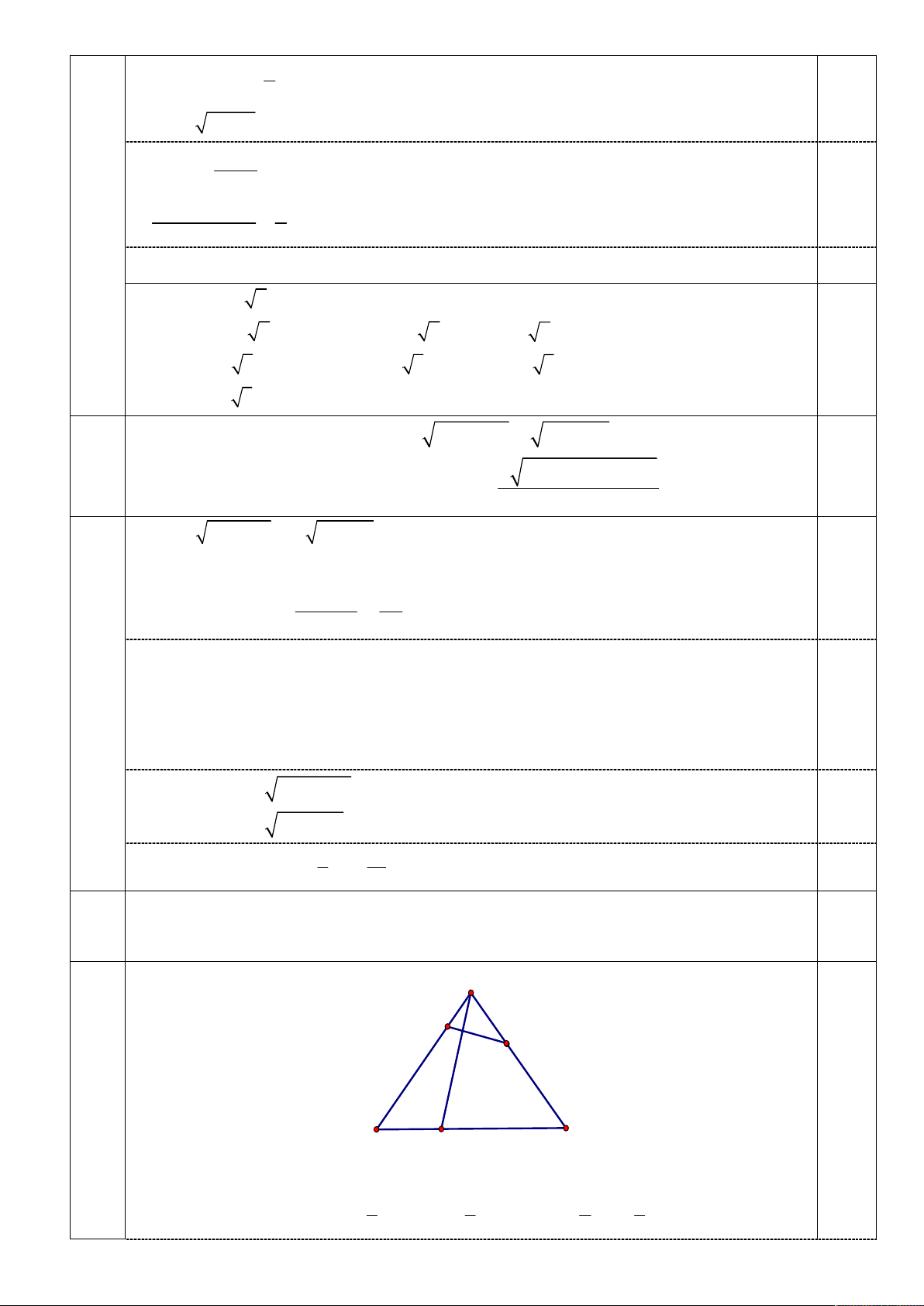
(2,0 điểm). Cho tam giác ABC đều cạnh 3a. Lấy các điểm M, N lần lượt trên các 7
cạnh BC, CA sao cho BM =a, CN=2a. Gọi P là điểm nằm trên cạnh AB sao cho
AM vuông góc với PN. Tính độ dài PN theo a. A P N 0,5 B C M  
Đặt AP  x AB  x  0   
 1   1   2  1 
Ta có: AM  AB BM  AB  BC  AB   AC  AB  AB  AC 3 3 3 3     1 
PN  PA  AN  x AB  AC 3    2  1     1 
AM  PN  AM .PN  0   AB  AC  x AB  AC  0      3 3   3  2x 1    2
x   2  a  2 2    a  a   AB.AC  0 2 0   A .
B AC  a cos 60    0,5 3 9  9 3  2   2 2x 1  2 x  a 2x 1  2 x  1 4 2 2   a  a    0       0  x      3 9  9 3  2 3 9  9 3  2 15 2  4  1   4  1   Khi đó 2 PN   AB 
AC  PN   AB  AC   15 3  15 3  0,5 2 16 1 8 a 21 2 2  a  a  .  225 9 45 2 225 21  PN  0,5 15
(2,0 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có
BC  2 AB , phương trình đường trung tuyến xuất phát từ đỉnh B là 8  
d  : x  y  2  0 . Biết 0
ABC  120 và A3; 
1 . Tìm tọa độ các đỉnh còn lại của tam giác. B A C M 0,5
Đặt AB  a a  0 Ta có: 2 2 0 AC 
AB  AC  2 A .
B ACcos120  a 7 2 2 2 2 2 2 AB  BC AC a 4a 7a a 3  BM      2 4 2 4 2 2 2 3a 7a Ta có 2 2 2 2
AB  BM  a    AM 4 4 0,5
Suy ra tam giác ABM vuông tại B.
Khi đó phương trình AB: x  y  2  0
B là giao của AB và BM  B 2; 0 0,5 6
Ta có: AB  d  ,
A BM   2  a  2  BM  2 6 3 0,5 Gọi M  ;
m 2  m . BM   m  2  2 2
M là trung điểm AC nên C 2  3;4  3 hoặc C 2  3;4  3
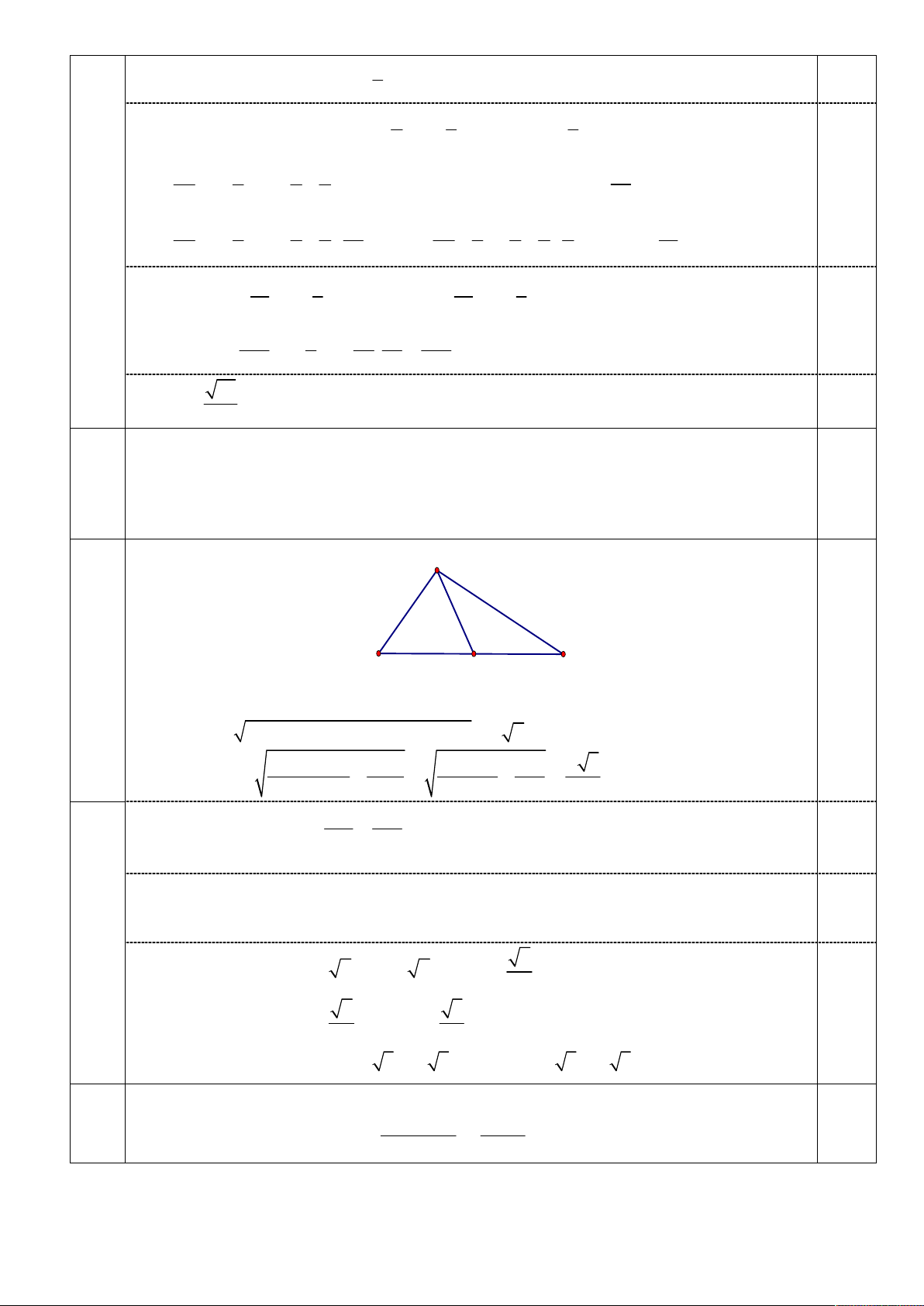
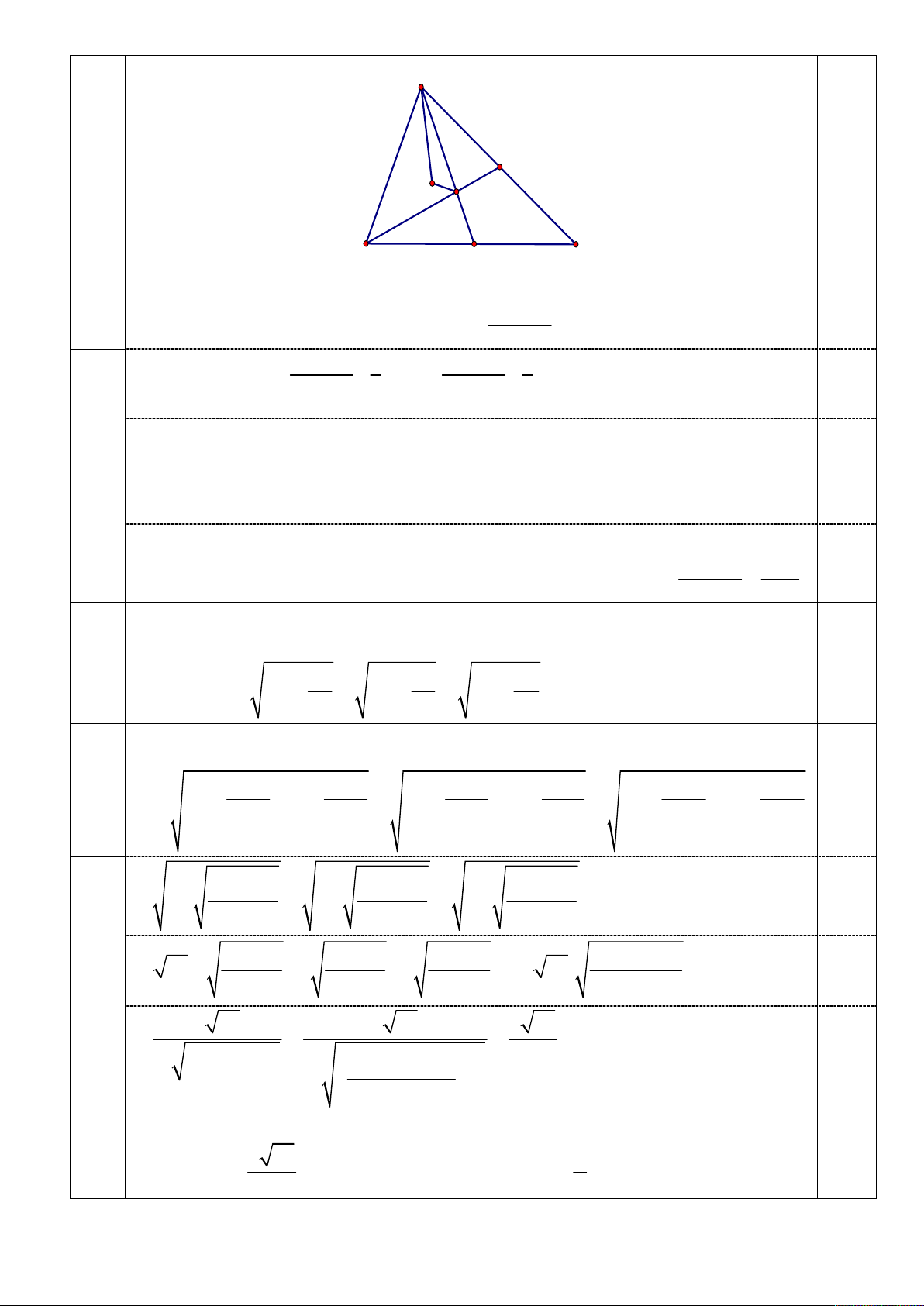
(2,0 điểm). Cho tam giác ABC gọi I là tâm đường tròn nội tiếp A  BC , biết 9
a  b  c 2ab
IG  IC . Chứng minh rằng 
(Với AB  c, BC  a,CA  b ). 3 a  b C N I G 0,5 A B M    
Ta chứng minh a IA  bIB  c IC  0         
 a IC  CA  bIC  CB 1
 cIC  0  CI 
 .aCA .bCB
a  b  c     a 1    b 1  
 GI  CI  CG   CA   CB    
 a  b  c 3 
 a  b  c 3  0,5     
Khi đó  2a  b  cCA  2b  a  cCB 
 aCA  bCB  0  
 ab  C .
A CB  b2a  b  c  a 2b  a  c  0 0,5     Do ab  C .
A CB  ab  ab cos C  ab 1 cos C   0
Nên ta có: b 2a  b  c  a 2b  a  c  0
a  b  c 2ab 0,5
 b 3a  a  b  c  a 3b  a  b  c  0  6ab  a  ba  b  c   3 a  b 3
(2,0 điểm). Cho các số thực a, ,
b c  0 thỏa mãn a  b  c  . Tìm giá trị nhỏ 2 10 2 1 2 1 2 1 nhất của S  a   b   c  . 2 2 2 b c a Ta thấy 2 1 1 2 1 1 2 1 1 S  a   ...   b   ...   c   ...  0,5 2 2 2 2 2 2 16b 16b 16c 16c 16a 16a    16 16 16 2 2 2 a a a 17 17 17  17  17  17 0,5 16 32 16 32 16 32 16 b 16 b 16 b  a b c  1  17 17  17  17  3 1717  0,5 8 16 8 16 8 16  8 5 5 5 16 b 16 c 16 a 16 a b c   3 17 3 17 3 17     a b c5 15 17 2 2 2 2 2
 2a  2b  2c 17  2    3  0,5 3 17 1 Vậy MinS 
. Dấu “=” xảy ra  a  b  c  . 2 2