Đề KSCL HSG Toán 12 lần 2 năm 2024 – 2025 khối THPT Triệu Sơn & Lê Lợi – Thanh Hóa
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề khảo sát chất lượng học sinh giỏi liên trường môn Toán 12 lần 2 năm học 2024 – 2025 khối THPT Triệu Sơn & THPT Lê Lợi, tỉnh Thanh Hóa. Đề thi gồm 20 câu trắc nghiệm nhiều phương án lựa chọn + 06 câu trắc nghiệm đúng sai + 06 câu trắc nghiệm trả lời ngắn, thời gian làm bài 90 phút. Kỳ thi được diễn ra vào ngày 22 tháng 11 năm 2024. Đề thi có đáp án và lời giải chi tiết mã đề 121.
Chủ đề: Đề HSG Toán 12 360 tài liệu
Môn: Toán 12 4.3 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI THANH HÓA
LIÊN TRƯỜNG LẦN 2 NĂM HỌC 2024 – 2025
KHỐI THPT TRIỆU SƠN - THPT LÊ LỢI MÔN: TOÁN.
Thời gian làm bài: 90 phút (ĐỀ CHÍNH THỨC) Ngày khảo sát: 22/11/2024 MÃ ĐỀ: 121. (Đề gồm 06 trang)
Họ tên thí sinh……………………………….; SBD………….… ;.Chữ kí của CBCT:………….………….
PHẦN I. (8,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến
câu 20. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Cho hàm số y = f (x) liên tục trên và có đạo hàm f ′(x) = (x + )2 (x − )3 1 1 (2 − x) . Hàm x số y = f +
1 đồng biến trên khoảng nào dưới đây? 2 A. ( 1; − ) 1 . B. (0; ) 1 . C. ( ; −∞ − ) 1 . D. (2;+∞).
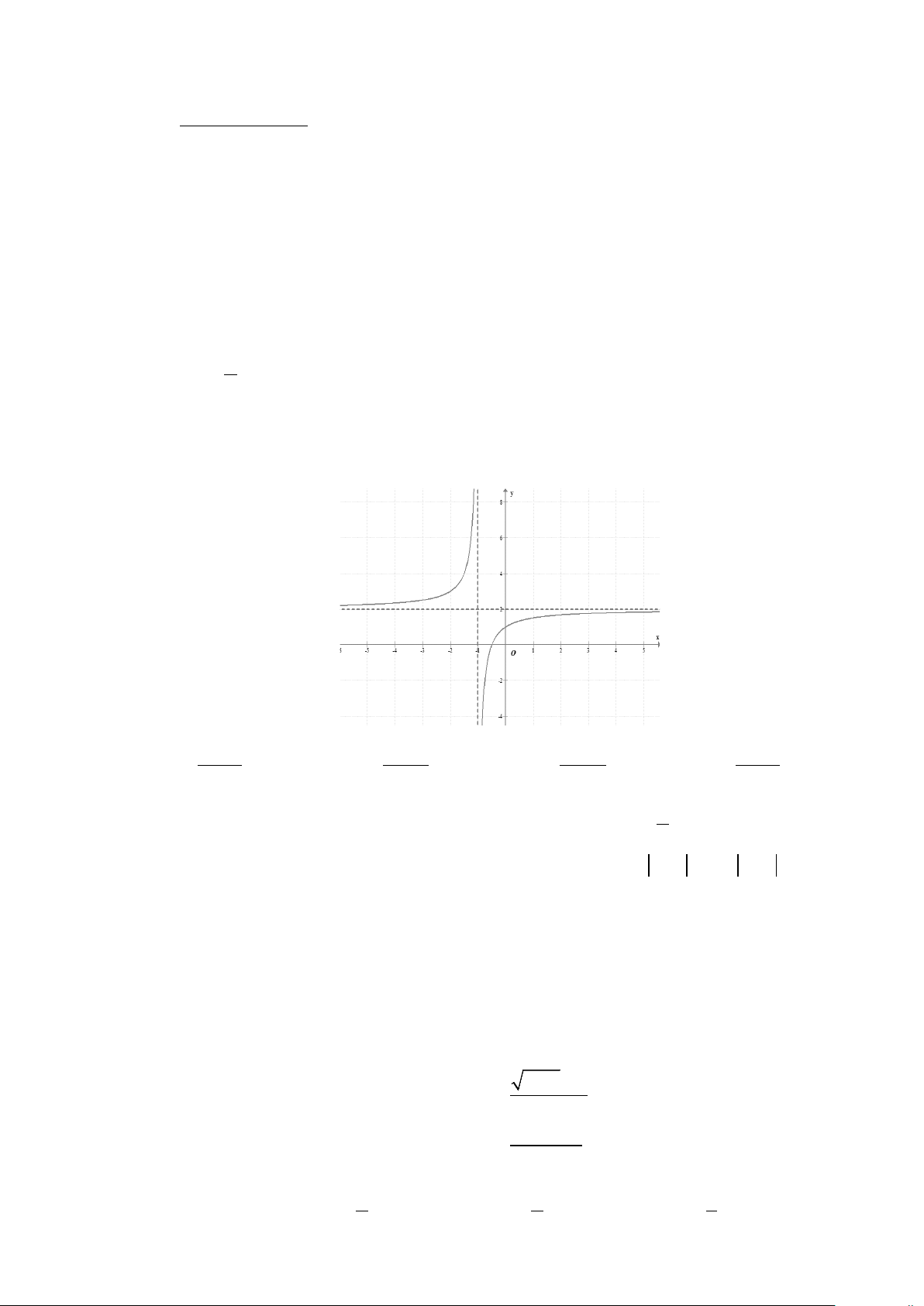
Câu 2: Hình vẽ bên dưới là đồ thị của hàm số nào A. 2x −1 y x − + x + = . B. 2 3 y = . C. 2x 3 y = . D. 2 1 y = . x +1 x +1 x +1 x +1 Câu 3: Cho hàm số 5 3
f (x) = ax + bx + cx (a > 0,b > 0) thỏa mãn 7
f (3) = − ; f (9) = 81. Gọi S là tập 3
hợp tất cả các giá trị của tham số m sao cho max g(x) + min g(x) = 86 với [ 1 − ;5] [ 1 − ;5]
g(x) = f (1− 2x) + 2 f (x + 4) + m . Tổng các phần tử của S là A. 74 − . B. 11. C. 5. D. 75 − .
Câu 4: Cho một cấp số nhân với công sai q = 3,u =12 . Tìm tổng của số hạng thứ tư và số hạng thứ 5
tám của cấp số nhân đó. A. 324. B. 332. C. 328. D. 976. x + 4 − 2 khi x > 0
Câu 5: Giá trị của tham số m sao cho hàm số ( ) x f x =
liên tục tại x = 0 là m(8 − 5x) khi x ≤ 0 4 A. 3 . B. 4 . C. 1 . D. 1 . 3 2 8
Trang 1/6 - Toán - Mã đề 121
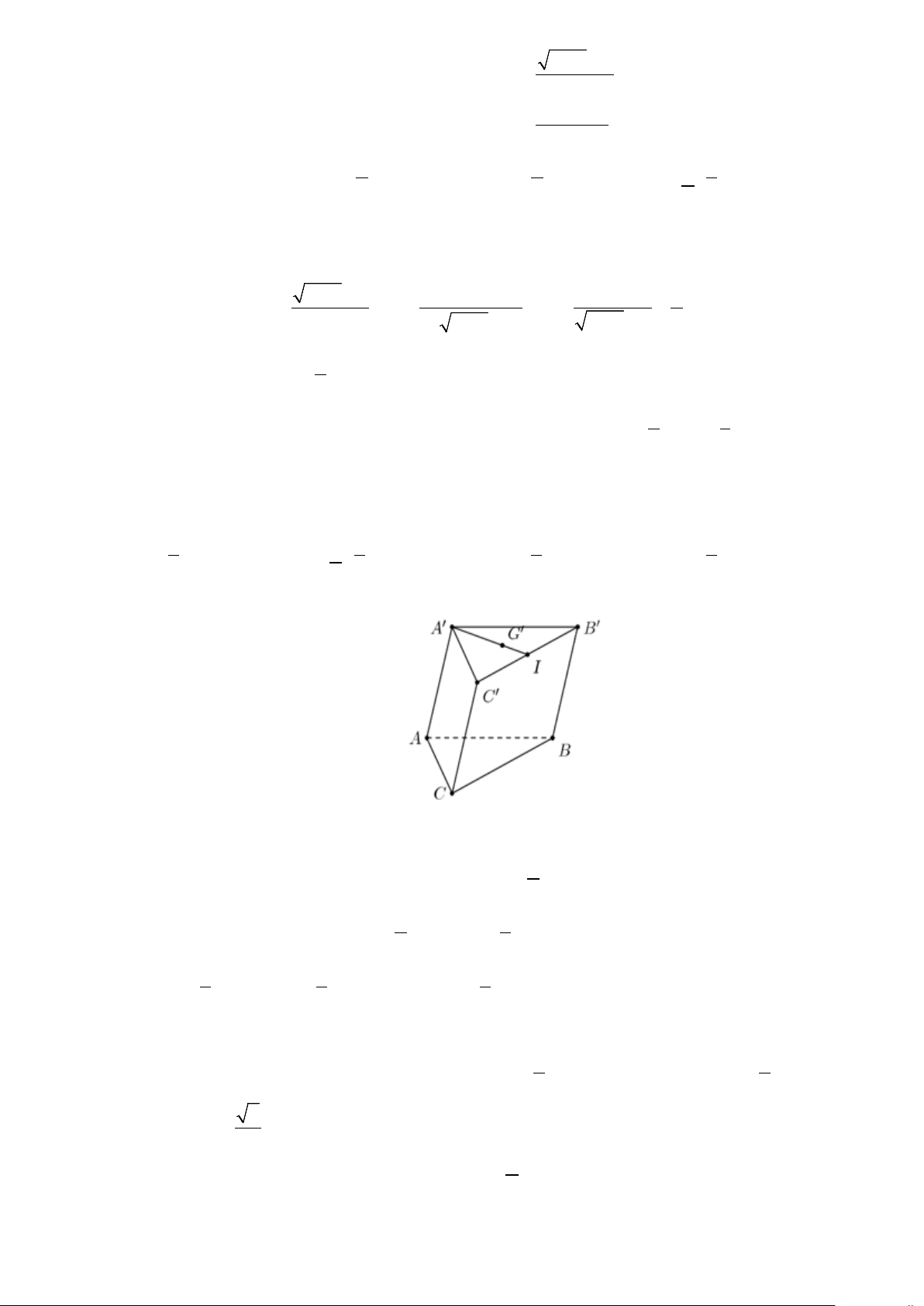
Câu 6: Cho hình lăng trụ ABC.A′B C
′ ′. Đặt a = AA ,′b = AB,c = AC . Gọi G′ là trọng tâm của tam giác A′B C
′ ′ . Véc tơ AG′ bằng
A. 1 (a +3b + c) .
B. 1 (3a +b + c) .
C. 1 (a +b +3c) .
D. 1 (a +b + c). 3 3 3 3
Câu 7: Cho hình hộp chữ nhật ABC .
D EFGH có AB = AE = 2, AD = 3 và đặt
a = AB,b = AD,c = AE . Lấy điểm M thỏa 1
AM = AD và điểm N thỏa 2
EN = EC , độ dài 5 5 đoạn a MN = với a ,b + ∈
∈ . Tính a + b b A. 64 . B. 65. C. 66 . D. 68.
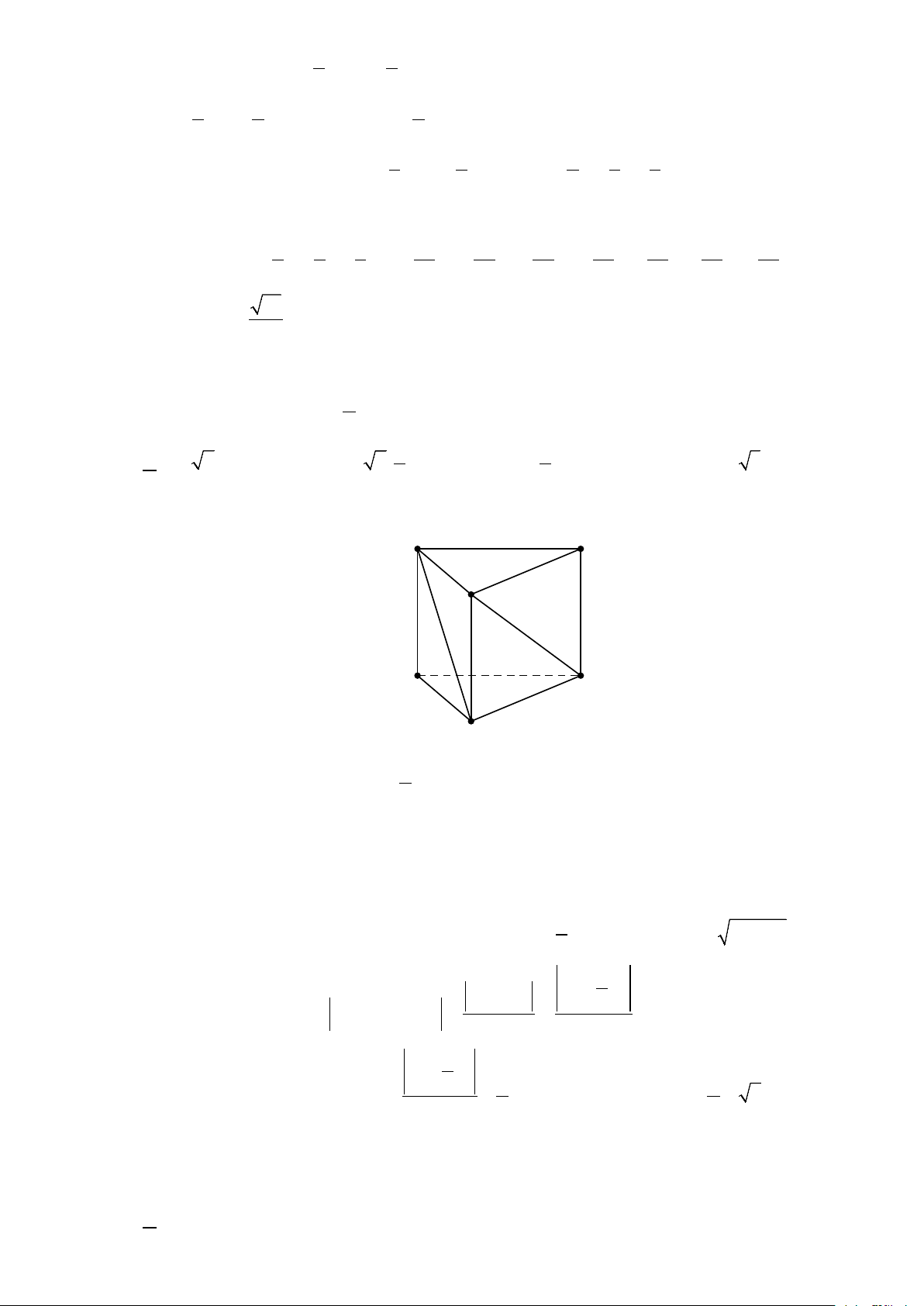
Câu 8: Cho hình lăng trụ tam giác đều ABC.A B C
1 1 1 có cạnh đáy bằng x và chiều cao bằng y . Để
Góc ( AC ,CB > 60° thì y thuộc khoảng nào 1 1 ) x A. (0; 2). B. 3 2; . C. 3 ;2 . D. (2;2 3) . 2 2
Câu 9: Trong không gian với hệ tọa độ Oxyz , cho OM = (1;5;2), ON = (3;7; 4 − ) , K ( 1; − 3; ) 1 . Gọi
P là điểm đối xứng với M qua N . Tìm tọa độ vectơ KP . A. KP = (6;6; 1 − ) 1 . B. KP = (8;6; 1 − )
1 . C. KP = (6;6; 4
− ). D. KP = (3;3; 2 − ).
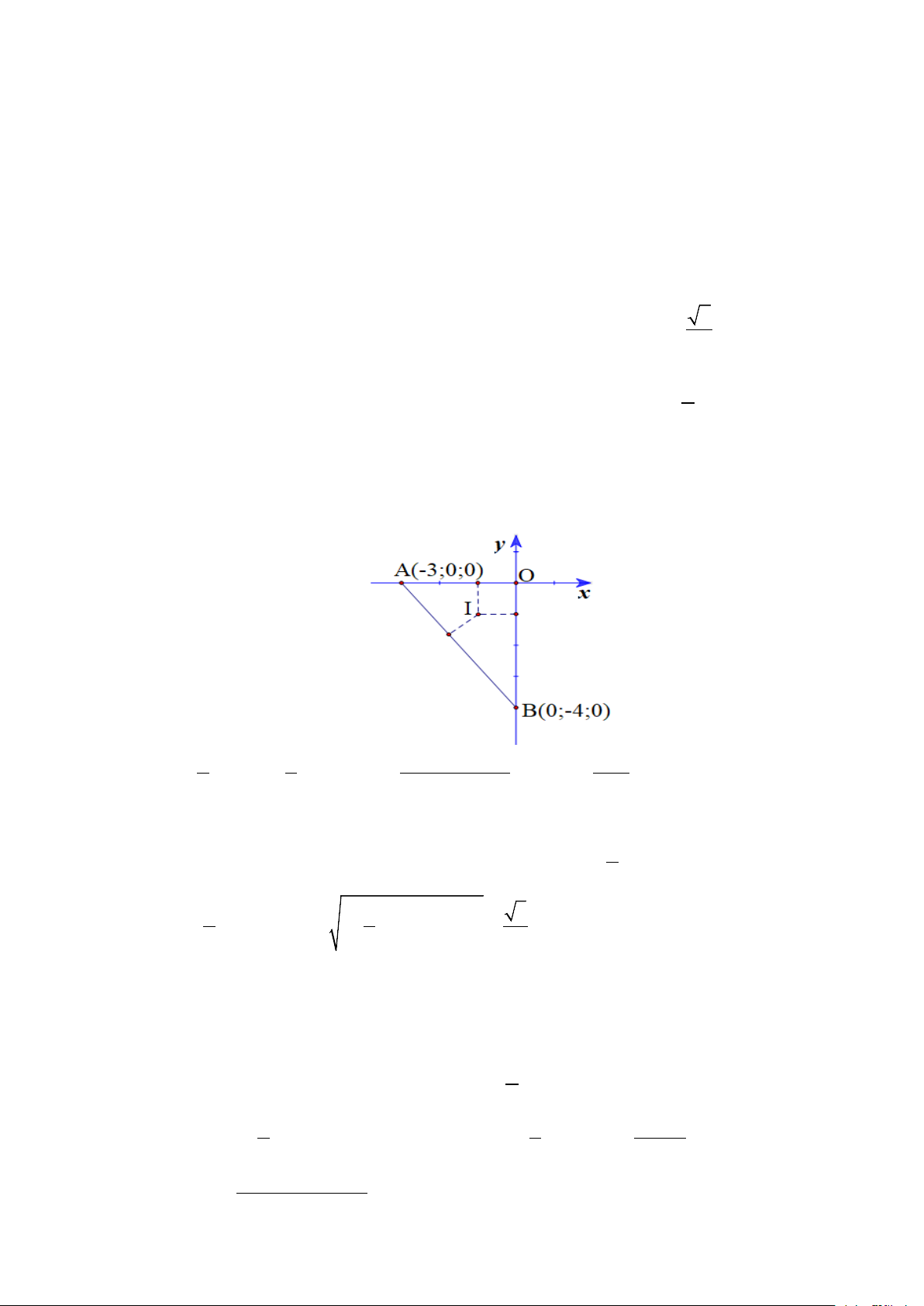
Câu 10: Trong không gian Oxyz , cho điểm A( 3 − ;0;0) , B(0; 4;
− 0) . Gọi I , J lần lượt là tâm đường
tròn nội tiếp và ngoại tiếp của tam giác OAB . Độ dài đoạn thẳng a IJ = với a ,b + ∈ ∈ . b Tính 2a + b A. 8 . B. 9 . C. 10. D. 12.
Câu 11: Trong không gian với hệ toạ độ Oxyz , cho ba điểm A( 2 − ;3; )
1 , B(2;1;0) , C ( 3 − ;−1; ) 1 . Biết
tọa độ điểm D( ;
x y; z) sao cho ABCD là hình thang có đáy AD và S = S .Tính ABCD 3 ABC ∆
x + y + z A. 8 . B. 9 − . C. 10 − . D. 12.
Câu 12: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a . Gọi I là trung điểm của AB ,
hình chiếu của S lên mặt phẳng ABC là trung điểm của CI , góc giữa SA và mặt đáy bằng
45. Gọi G là trọng tâm tam giác SBC . Khoảng cách giữa hai đường thẳng SA và CG bằng
a m ( ,mn∈,m <100).Tính m+n? n A. 35. B. 22 . C. 99. D. 28 .
Trang 2/6 - Toán - Mã đề 121
Câu 13: Cho mẫu số liệu về chiều cao (cm) của các học sinh nữ trong khối 11 của một trường như sau:
Giá trị đại diện của nhóm [155;160) là A. 157,5. B. 155 . C. 157 . D. 160.
Câu 14: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một chi nhánh của doanh
nghiệp được ghi lại dưới bảng sau ( đơn vị: triệu đồng):
Hãy tính tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm)? A. 7,86. B. 7,68. C. 7,81. D. 7,56.
Câu 15: Gọi M ,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số π f (x) 2 4cos x 2 sin 2x = + −
. Tính giá trị biểu thức 2 2
T = M + m . 4 A. T =14 . B. T =15 . C. T =12 . D. T =17 .
Câu 16: Cho phương trình 2 π 2 π
sin x sin 5x 2cos x 2cos 2x + = − − +
. Số vị trí biểu diễn các 4 4
nghiệm của phương trình trên đường tròn lượng giác là ? A. 1. B. 2 . C. 4 . D. 6 . x
Câu 17: Cho hàm số f (x) 9 =
, x ∈ R . Nếu a + b = 3 thì f (a) + f (b − 2) có giá trị bằng 3+ 9x A. 1. B. 2 . C. 1 D. 3 . 4 4
Câu 18: Có bao nhiêu giá trị nguyên thuộc khoảng ( 9;
− 9) của tham số m để bất phương trình x ≤ ( 2 3log
2log m x − x − (1− x) 1− x ) có nghiệm thực? A. 6 . B. 7 . C. 10. D. 11.
Câu 19: Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26 . Bạn Hải rút ngẫu nhiên cùng một lúc
bốn tấm thẻ trong hộp . Hỏi có bao nhiêu cách rút bốn tấm thẻ sao cho bất kỳ hai trong bốn tấm
thẻ lấy ra đó có hai số tương ứng trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị? A. 2024. B. 8855. C. 7315. D. 10626.
Câu 20: Gọi A là tập hợp tất cả các số tự nhiên có tám chữ số. Chọn ngẫu nhiên một số thuộc A , tính
xác suất để số tự nhiên được chọn chia hết cho 7 ?(Kết quả làm tròn đến hàng phần trăm) A. 0,17 . B. 0,14. C. 0,21. D. 0,12.
Trang 3/6 - Toán - Mã đề 121
PHẦN II. (7,2 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 6. Trong mỗi
ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. 2
Câu 1: Cho hàm số y = f (x) x + x −5 = . x + 3
a) Hàm số nghịch biến trên ( 7; − − 3) .
b) Đồ thị hàm số có đường tiệm cận xiên tạo với 2 trục tọa độ một tam giác có diện tích bằng 2 .
c) Có 15 giá trị nguyên của tham số p thuộc khoảng (0;20) để đồ thị hàm số số 2024 y = f (x) + p
có đúng ba đường tiệm cận.
d) Có 2022 giá trị nguyên của tham số m thuộc [ 2024 − ;2025] để hàm số
g (x) = f ( 2x − 2x − m) có 5 điểm cực trị.
Câu 2: Trong không gian Oxyz , cho ba điểm A(0;0;− ) 1 , B( 1; − 1;0), C (1;0; ) 1 . − − a) Điểm 1 1 1
I( ; ; ) là trung điểm của đoạn thẳng AB . 2 2 2
b) Khi tứ giác ABCD là hình bình hành thì D O = 6 . c) Điểm H ( ; a ;
b c) là chân đường cao kẻ từ A xuống cạnh BC của tam giác ABC . Khi đó 5
a + b + c = . 3
d) Biết điểm M ( ;
x y; z) để biểu thức 2 2 2
3MA + 2MB − MC đạt giá trị nhỏ nhất, khi đó
4x-2y+z = 2024 .
Câu 3: Cho hình hộp chữ nhật ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh bằng a . Gọi M ,
N , P theo thứ tự là trung điểm của các cạnh A′B′ , CC′ , AD . Biết rằng BM và NP vuông góc với nhau.
a) Góc giữa hai đường thẳng AC và MP bằng 90° .
b) Khoảng cách giữa hai đường thẳng BP và MC′ bằng a 2 .
c) Nếu ϕ là góc giữa hai mặt phẳng (MNP) và ( ABCD) thì 3 cosϕ = . 3
d) Thể tích khối tứ diện AMNP bằng 1 3 a . 16
Câu 4: Một hộp đựng 9 tấm thẻ được đánh số từ 1 đến 9. Ký hiệu X = {1;2;3;4;5;6;7;8; } 9 . Xét phép
thử: “Rút ngẫu nhiên n tấm thẻ từ hộp đã cho”.
a) Mỗi tập con gồm 3 thẻ được lấy từ hộp là số tổ hợp chập 3 của 9.
b) Mỗi số có 3 chữ số đôi một khác nhau lập từ X là một chỉnh hợp chập 3 của 9.
c) Số tập con của tập X là 256 .
d) Gọi A là biến cố: “Có ít nhất một thẻ ghi số chia hết cho 3”. Số lần rút tấm thẻ để xác suất
của biến cố A bằng 83 là 6 . 84
Trang 4/6 - Toán - Mã đề 121
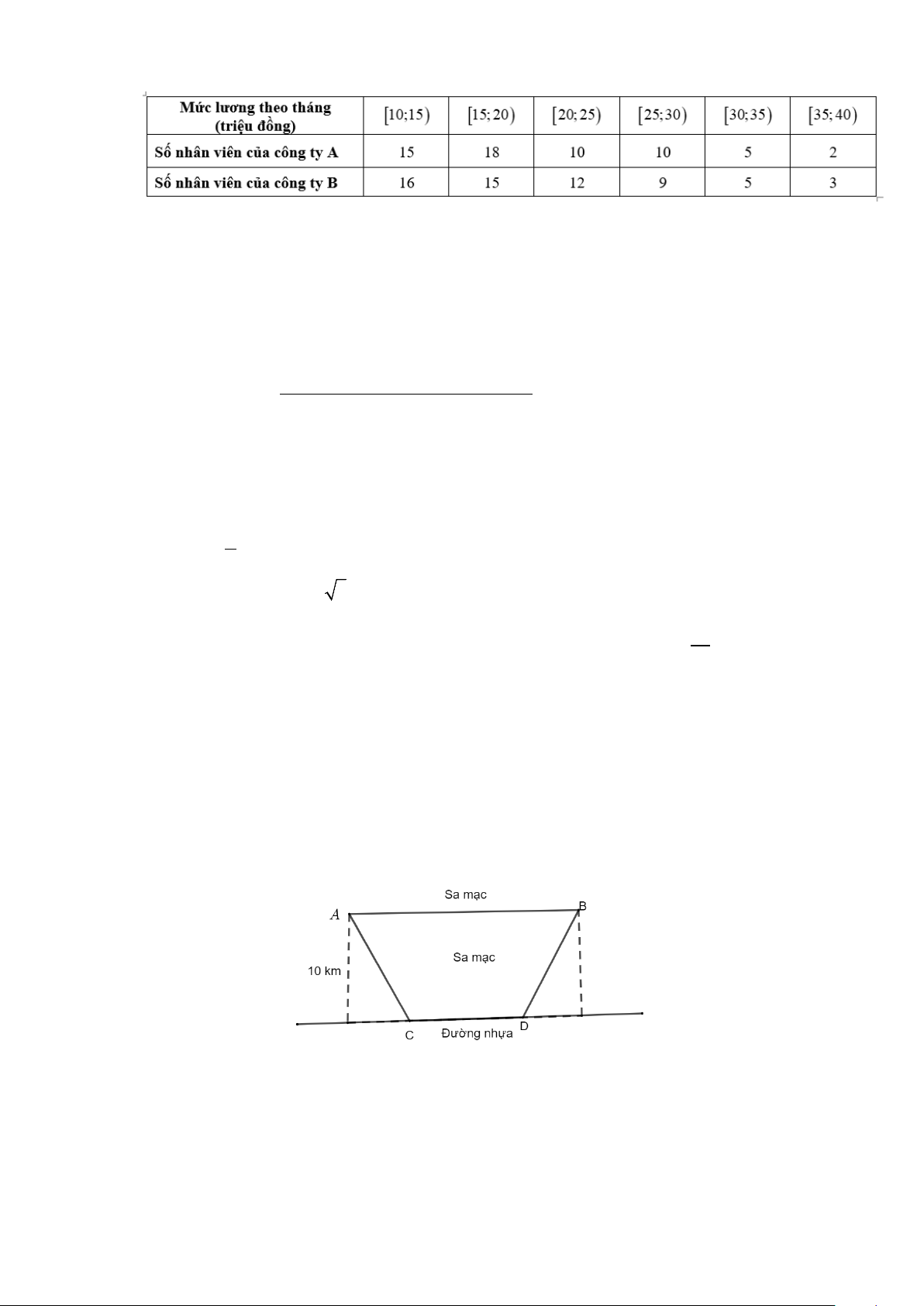
Câu 5: Mức lương theo tháng (đơn vị: triệu đồng) của nhân viên ở hai công ty A, B như sau:
a) Mức lương trung bình theo tháng của nhân viên ở công ty A là 20,67 triệu đồng (làm tròn đến hàng phần trăm).
b) Đối với công ty A, nhân viên có mức lương tối đa khoàng 18 triệu đồng.
c) Đối với công ty B, 25% số nhân viên có mức lương từ 26,11 triệu đồng trở lên (làm tròn đến hàng phần trăm).
d) Công ty A có mức lương đồng đều hơn công ty B? Câu 6: cos . x cos2x − .
m cos x + cos2x − m Cho phương trình
= 0 với m là tham số. sin x
a) Điều kiện xác định của phương trình là x ≠ kπ (k ∈).
b) Với m =1, phương trình đã cho có 2 nghiệm thuộc [0;2π ] 1
c) Khi m = các nghiệm của phương trình được biểu diễn trên đường tròn lượng giác là một đa giác. 2
Diện tích đa giác đó bằng 3 . 2
d) Có hai giá trị m để 4m nguyên và phương trình có đúng 2 nghiệm x π ;0 ∈ 3 .
PHẦN III. (4,8 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Một nhà địa chất học đang ở tại điểm A trên sa mạc. Anh ta muốn đến điểm B và cách A một
đoạn là 70km . Trong sa mạc thì xe anh ta chỉ có thể di chuyển với vận tốc là 30km/h . Nhà địa
chất phải đến được điểm B sau 2 giờ. Vì vậy, nếu anh ta đi từ A đến B sẽ không thể đến đúng
giờ được. May mắn thay, có một con đường nhựa song song với đường nối A và B và cách AB
một đoạn 10km . Trên đường nhựa đó thì xe nhà địa chất này có thể di chuyển với vận tốc
50km/h . Thời gian ngắn nhất để nhà địa chất di chuyển từ A đến B là bao nhiêu phút. Câu 2: Cho hàm số
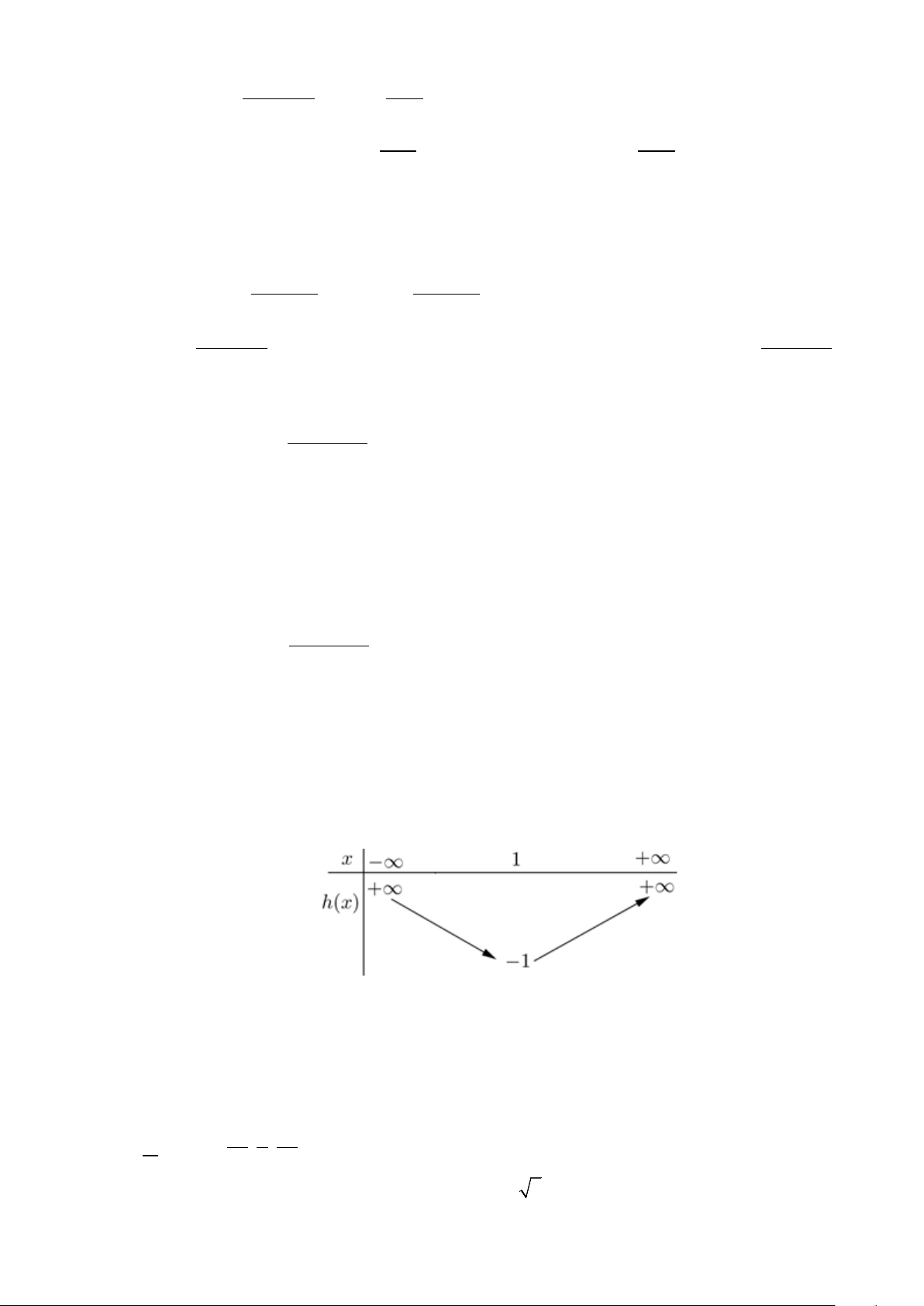
y = f (x) liên tục trên tập R , biết 2024 2025
f ′ x = x x − ( 2 2 ( ) ( 2)
x −8x + m − 3m − 4), x
∀ ∈ R . Gọi S là tập tất cả các giá trị nguyên
của tham số m để đồ thị hàm số y = f (| x |) có 5 điểm cực trị. Tính tổng tất cả các giá trị của các
phần tử của tập hợp S .
Trang 5/6 - Toán - Mã đề 121
Câu 3: Trong không gian với hệ tọa độOxyz , cho hai điểm A(2;2;0), B(2;0; 2 − ) và điểm
M (a,b,c) với a,b,c là các số thực thay đổi thỏa mãn a + 2b − c −1 = 0 . Biết MA = MB và góc
AMB có số đo lớn nhất. Tính S = . a .
b c (kết quả làm tròn đến hàng phần chục)
Câu 4: Bạn Hoa chọn ngẫu nhiên 3 số phân biệt trong tập hợp {1,2,3,4,5,6,7,8, } 9 và sắp xếp chúng
theo thứ tự giảm dần để tạo thành một số gồm ba chữ số. Bạn Bình chọn ngẫu nhiên 3 số phân
biệt trong tập hợp {1,2,3,4,5,6,7, }
8 và sắp xếp chúng theo thứ tự giảm dần để tạo thành một số
gồm ba chữ số. Tìm xác suất sao cho số của Hoa lớn hơn số của Bình (Kết quả làm tròn đến hàng phần trăm).
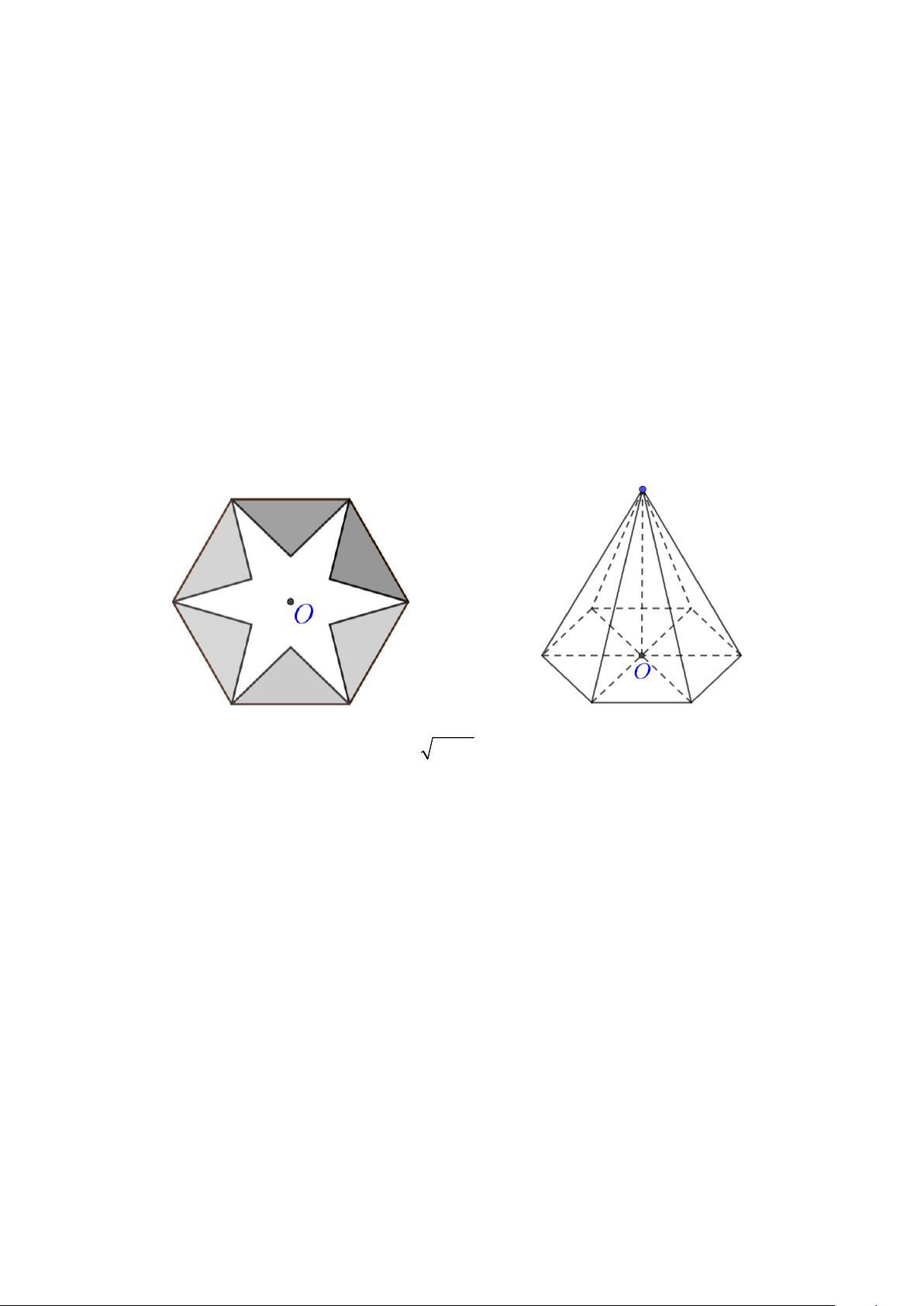
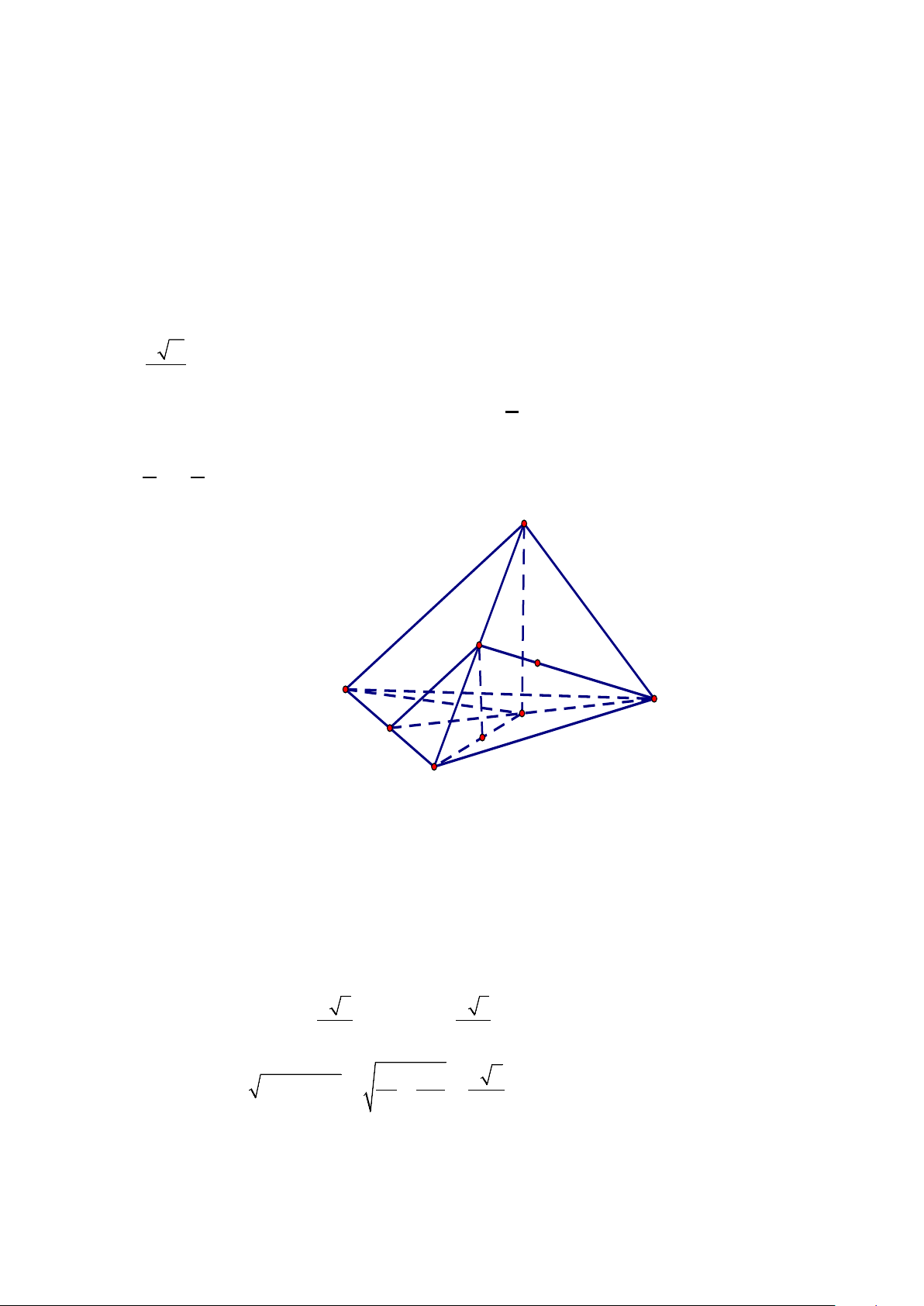
Câu 5: Cho tấm tôn hình lục giác đều cạnh 24cm . Người ta cần làm một hình chóp lục giác đều bằng
cách cắt bỏ đi các phần tô đậm là các tam giác cân, sau đó gập và hàn lại (các đường hàn không
đáng kể) thành hình chóp lục giác đều (như hình vẽ dưới đây). Thể tích lớn nhất khối chóp tạo
thành bằng bao nhiêu? (Kết quả làm tròn đến hàng đơn vị)
Câu 6: Cho hàm số ( ) − x x f x = − − ( 2 4
4 ln x + 1+ x ) . Tìm số giá trị nguyên m∈[ 2024 − ;2024] để bất phương trình f ( 2
x + 2mx + sin x) + f (4x −sin x − 2m +1 )
1 ≥ 0 nghiệm đúng x ∀ ∈[2;6] ? …………HẾT………
Thí sinh thực hiện nghiêm túc Quy chế thi. CBCT không giải thích gì thêm
Trang 6/6 - Toán - Mã đề 121
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI THANH HÓA
LIÊN TRƯỜNG LẦN 2 NĂM HỌC 2024 – 2025
KHỐI THPT TRIỆU SƠN - THPT LÊ LỢI MÔN: TOÁN
(ĐÁP ÁN CHÍNH THỨC)
I. ĐÁP ÁN ĐỂ CHẤM BÀI Câu Mã đề 121 1 B 2 D 3 A 4 C 5 D 6 B 7 C 8 A 9 A 10 D 11 C 12 C 13 A 14 A 15 C 16 D 17 A 18 B 19 B 20 B 1 SĐSĐ 2 ĐSSS 3 ĐSĐĐ 4 SĐSĐ 5 ĐSĐĐ 6 ĐSĐĐ 1 116 2 9 3 0 4 0,66 5 1142 6 2013 1
II. HDG CÁC CÂU VẬN DỤNG VÀ VẬN DỤNG CAO.
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 20.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: [2] Cho hàm số y = f (x) liên tục trên và có đạo hàm f ′(x) = (x + )2 (x − )3 1 1 (2 − x) . x
Hàm số y = f +
1 đồng biến trên khoảng nào dưới đây? 2 A. ( 1; − ) 1 . B. (0; ) 1 . C. ( ; −∞ − ) 1 . D. (2;+∞). Lời giải Chọn B x = 1 − Ta có f (x) 0 (x )2 1 (x )3 1 (2 x) 0 ′ = ⇔ + − − = ⇔ x =1 . x = 2
Lập bảng xét dấu của f ′(x) ta được: x x
Ta có 1 < +1 < 2 ⇔ 0 < x < 2 y f =
+ đồng biến trên khoảng (0; ) 1 . 2 suy ra hàm số 1 2
Câu 2: [1] Hình vẽ bên dưới là đồ thị của hàm số nào A. 2x −1 y x − + x + = . B. 2 3 y = . C. 2x 3 y = . D. 2 1 y = . x +1 x +1 x +1 x +1
Chọn D Đồ thị hàm số cắt trục Oy tai điểm có tọa độ(0; ) 1 nên chọn phương 2 Câu 3: Cho hàm số 5 3
f (x) = ax + bx + cx (a > 0,b > 0) thỏa mãn 7
f (3) = − ; f (9) = 81. Gọi S là tập 3
hợp tất cả các giá trị của tham số m sao cho max g(x) + min g(x) = 86 với [ 1 − ;5] [ 1 − ;5]
g(x) = f (1− 2x) + 2 f (x + 4) + m . Tổng các phần tử của S là A. 74 − . B. 11. C. 5. D. 75 − . Lời giải Chọn A
Ta có g '(x) = 2
− f '(1− 2x) + 2 f '(x + 4); g '(x) = 0 ⇔ f '(1− 2x) = f '(x + 4) 4 2
f '(x) = 5ax + 3bx + c ⇒ f '(x + 4) = f '(1− 2x)
⇔ a(x + )4 + b(x + )2 = a( − x)4 + b( − x)2 5 4 3 4 5 1 2 3 1 2
⇔ (x + 4)2 − (1− 2x)2 5a
( x + 4)2 + (1− 2x)2 ) + 3b = 0 . ⇔ ( = −
x + )2 = ( − x)2 x 1 4 1 2 ⇔ x =5
Do đó g '(x) không đổi dấu trên [ 1; − 5] . g( 1
− ) = f (3) + 2 f (3) + m = m − 7 . g(5) = f ( 9)
− + 2 f (9) + m = m + 81. Vì 5 3
f (−x) = −ax − bx − cx = − f (x) .
Suy ra m − 7 ≤ g(x) ≤ 81+ m với x ∀ ∈[ 1; − 5].
TH1: m ≥ 7 ⇒ m − 7 ≥ 0;m + 81 > 0.
max g(x) + min g(x) = 81+ m + m − 7 = 86 ⇔ m = 6 (loại) [ 1 − ;5] [ 1 − ;5] TH2: m ≤ 81
− ⇒ m − 7 < 0;m + 81≤ 0
max g(x) + min g(x) = 7 − m − m −81 = 86 ⇔ m = 80 − (loại) [ 1 − ;5] [ 1 − ;5]
TH3: 81 < m < 7⇒ m + 81 > 0; m − 7 < 0 .
max g(x) + min g(x) = 81+ m + 0 = 86 ⇔ m = 5 (thỏa mãn) [ 1 − ;5] [ 1 − ;5]
Hoặc max g(x) + min g(x) = 7 − m + 0 = 86 ⇔ m = 7 − 9 (thỏa mãn). [ 1 − ;5] [ 1 − ;5] Vậy m = 7
− 9;m = 5 . Suy ra tổng các giá trị của các phần tử của S là 79 − + 5 = 74 −
Câu 4: [1] Cho một cấp số nhân với công sai q = 3,u =12 . Tìm tổng của số hạng thứ tư và số hạng 5
thứ tám của cấp số nhân đó. A. 324. B. 332. C. 328. D. 976. Lời giải Chọn C Ta có: n 1 − 4 4 4
u = u q ⇒ u = u ⇔ = u ⇔ u = . Suy ra: 3 4 3
u = u .q = .3 = 4 và n .3 12 .3 1 5 1 1 1 27 4 1 27 7 4 7
u = u .q =
.3 = 324 . Từ đó suy ra: u + u = 4 + 324 = 328 . 8 1 27 4 8 3 x + 4 − 2 khi x > 0
Câu 5: [2] Giá trị của tham số m sao cho hàm số ( ) x f x =
liên tục tại x = 0 là m(8 − 5x) khi x ≤ 0 4 A. 3 . B. 4 . C. 1 . D. 1 . 3 2 8 Lời giải Chọn D Có f (x) x + 4 − 2 lim 1 1 = lim = lim x = lim = . x 0+ x 0+ → → x x 0+ →
x( x + 4 + 2) x 0+ → x + 4 + 2 4 lim 5
f ( x) lim 2m x = − =
2m và f (0) = 2m . x 0− → x 0− → 4
Hàm số liên tục tại x = 0 ⇔ lim f ( x) = lim f ( x) = f (0) 1 1
⇔ 2m = ⇔ m = . x 0+ x 0− → → 4 8
Câu 6: [1] Cho hình lăng trụ ABC.A′B C
′ ′. Đặt a = AA ,′b = AB,c = AC . Gọi G′ là trọng tâm của tam giác A′B C
′ ′ . Véc tơ AG′ bằng
A. 1 (a +3b + c) .
B. 1 (3a +b + c) .
C. 1 (a +b +3c) .
D. 1 (a +b + c). 3 3 3 3 Lời giải
Gọi I là trung điểm của B C ′ ′
Vì G′ là trọng tâm của tam giác A′B C ′ ′ 2
⇒ A′G′ = A′I 3
Ta có : 2
AG′ = AA′ + A′G′ = AA′ + A′I 1
= AA′ + ( A′B′+ A′C′) 3 3
1
= AA + ( AB + AC) 1
= ( AA+ AB + AC) 1 3
= (3a +b + c). 3 3 3
Câu 7: [2] Cho hình hộp chữ nhật ABC .
D EFGH có AB = AE = 2, AD = 3 và đặt
a = AB,b = AD,c = AE . Lấy điểm M thỏa 1
AM = AD và điểm N thỏa 2
EN = EC , độ dài 5 5 đoạn a MN = với a ,b + ∈
∈ . Tính a + b b A. 64 . B. 65. C. 66 . D. 68. Lời giải 4 Ta có 1 1
MA = −AM = − AD = − b . 5 5
2 2
EN = EC = (EF + EH + EA) 2
= (a + b − c). 5 5 5
Ta có 1 2
MN = MA + AE + EN = − b + c + (a + b − c) 2 1 3
= a + b + c . 5 5 5 5 5
Vì a,b,c đôi một vuông góc nên . a b = . b c = . a c = 0 . 2 2 2 2 2 2 2 1 3 4 1 9 4 1 9 61 MN = MN =
a + b + c = a + b + c = .4 + .9 + .4 = . 5 5 5 25 25 25 25 25 25 25 Suy ra 61 MN =
nên a + b = 66. 5
Câu 8: [3] Cho hình lăng trụ tam giác đều ABC.A B C
1 1 1 có cạnh đáy bằng x và chiều cao bằng y . Để
Góc ( AC ,CB > 60° thì y thuộc khoảng nào 1 1 ) x A. (0; 2). B. 3 2; . C. 3 ;2 . D. (2;2 3) . 2 2 Lời giải A B C A1 B1 C1 Ta có 1 2 A . B AC = A .
B AC.cos60° = x . 2
AC = AC + AA 1 1
ACC A
1 1 là hình chữ nhật nên ta có AC = AC + AA . 1 1
CB = CB + CC = AB − AC + AA . 1 1 1
Ta có AC .CB = ( AC + AA ).( AB − AC + AA ) 2 1 2 = y − x và 2 2
AC = CB = x + y . 1 1 1 1 2 1 1 2 1 2 . y − x AC CB Khi đó ( AC CB ) = (AC CB ) 1 1 2 cos , cos , = = . 1 1 1 1 2 2 AC .CB x + y 1 1 2 1 2 y − x
Theo đề ( AC ,CB 2 1 y > 60° , suy ra 4 2 2
< ⇔ 3y − 6x y < 0 ⇔ 0 < < 2 . 1 1 ) 2 2 x + y 2 x
Câu 9: [1] Trong không gian với hệ tọa độ Oxyz , cho OM = (1;5;2), ON = (3;7; 4 − ) , K ( 1; − 3; ) 1 .
Gọi P là điểm đối xứng với M qua N . Tìm tọa độ vectơ KP . A. KP = (6;6; 1 − ) 1 . B. KP = (8;6; 1 − )
1 . C. KP = (6;6; 4
− ). D. KP = (3;3; 2 − ). 5 Lời giải
Ta có: OM = (1;5;2) ⇒ M (1;5;2) , ON = (3;7; 4 − ) ⇒ N (3;7; 4 − ) .
Vì P là điểm đối xứng với M qua N nên N là trung điểm của MP , ta suy ra được
x − x = x − x x = P 5 N M P N MN
= NP ⇔ y − y = y − y ⇔ y = ⇒ P − . P 9 (5;9; 10) N M P N
z − z = z − z z = − P 10 N M P N Khi đó KP = (6;6; 1 − ) 1 .
Câu 10: [2] Trong không gian Oxyz , cho điểm A( 3 − ;0;0) , B(0; 4;
− 0) . Gọi I , J lần lượt là tâm đường
tròn nội tiếp và ngoại tiếp của tam giác OAB . Độ dài đoạn thẳng a IJ = với a ,b + ∈ ∈ . b Tính 2a + b A. 8 . B. 9 . C. 10. D. 12. Lời giải Đáp số: 12. Ta có: OA = ( 3
− ;0;0) ⇒ OA = 3; OB = (0; 4;
− 0) ⇒ OB = 4; AB = (3; 4 − ;0) ⇒ AB = 5. OA ∆
B vuông tại O , nằm trong mặt phẳng (Oxy) . 1 1 S S = OAOB = = ; OA OB AB p + + = = 6 ABC ⇒ r = =1. OAB . . .3.4 6 2 2 2 p ⇒ I ( 1; − 1;
− 0) là tâm đường tròn nội tiếp OA ∆ B . Do OA ∆
B vuông tại O nên J là trung điểm của AB 3 J ; 2;0 ⇒ − − . 2 2 1 1 IJ IJ = − − ⇒ = − + (− )2 2 5 ; 1;0 1 + 0 =
.Nên 2a + b =12. 2 2 2
Câu 11: [3] Trong không gian với hệ toạ độ Oxyz , cho ba điểm A( 2 − ;3; )
1 , B(2;1;0) , C ( 3 − ;−1; ) 1 . Biết
tọa độ điểm D( ;
x y; z) sao cho ABCD là hình thang có đáy AD và S = S .Tính ABCD 3 ABC ∆
x + y + z A. 8 . B. 9 − . C. 10 − . D. 12. Lời giải Ta có: 1 S = AD + BC d A BC 1 S S AD BC ∆ ⇔ = + . ABCD ( ) 2 . ABC ABCD ( ). ( , ) 2 2 BC
(AD + BC).S ⇔ 3 ABC S ∆ =
⇔ 3BC = AD + BC ⇔ AD = 2BC . ABC ∆ BC 6
Mà ABCD là hình thang có đáy AD nên AD = 2BC ( ) 1 . BC = ( 5; − − 2; )
1 , AD = (x + y − z − . D 2; D 3; D ) 1 x + = − x = − D 12 D 2 10 ( )1 ⇔
y − = − ⇔ y = − . D 1 D 3 4 z − = z = D 3 D 1 2 Vậy D( 1 − 2;−1;3) .
Câu 12: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a . Gọi I là trung điểm của AB , hình
chiếu của S lên mặt phẳng ABC là trung điểm của CI , góc giữa SA và mặt đáy bằng 45.
Gọi G là trọng tâm tam giác SBC . Khoảng cách giữa hai đường thẳng SA và CG bằng
a m ( ,mn∈,m <100).Tính m+n? n A. 35. B. 22 . C. 99. D. 28 . Lời giải Chọn C S M G A C H I E a B
Gọi giao điểm của CG với SB là M . Suy ra M là trung điểm của SB .
Gọi E là chân đường vuông góc hạ từ M xuống mặt phẳng ABC.
Ta có AS / /IM AS / /IMC. Suy ra d S ,
A CG d S ,
A IMC d S,IMC d B,IMC. Theo bài ra ta có a 3 CI a suy ra 3 IH . 2 4 2 2 Suy ra 2 2 a 3a a 7
AH AI IH . 4 16 4 Do góc S , A ABC
45 suy ra tam giác S
HA vuông cân tại H . 7 Suy ra a 7 SH a AH . Suy ra 14 SA AH 2 . 4 4 Xét tam giác S BC : dễ thấy a 14 SB SA . 4 2 2 2 2SC 2BC SB a 38 2 2 a 10
SC SI SH IH . Suy ra CM . 4 4 8 Xét tam giác IMC : SA a 14 IM a a 33 , 38 CM , 3 CI . Suy ra 2 S . a 2 8 8 2 IMC 32
Thể tích khối chóp MIBC là: 1 1 SH 1 1 a 7 1 a a 3 21 3 V ME S . IC IB a MIBC . IBC . . . . . . . 3 3 2 2 3 8 2 2 2 192 21 3 3. a
Suy ra d S,MIC d B,MIC 3VMIBC 192 77 a . S IMC 33 22 2 a 32
Vậy m + n = 99 .
Câu 13: Cho mẫu số liệu về chiều cao (cm) của các học sinh nữ trong khối 11 của một trường như sau:
Giá trị đại diện của nhóm [155;160) là A. 157,5. B. 155 . C. 157 . D. 160.
Câu 14: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một chi nhánh của doanh
nghiệp được ghi lại dưới bảng sau ( đơn vị: triệu đồng):
Hãy tính tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên? (giá trị gần nhất) A. 7,86. B. 7,68. C. 7,81. D. 7,56.
Câu 15: [1] Gọi M ,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số π f (x) 2 4cos x 2 sin 2x = + −
. Tính giá trị biểu thức 2 2
T = M + m . 4 A. T =14 . B. T =15 . C. T =12 . D. T =17 . Lời giải Chọn C
Tập xác định: D = R . Ta có π f (x) 2 4cos x 2 sin 2x = + −
= 2 + 2cos 2x + sin 2x − cos 2x 4 8 π sin 2x cos 2x 2 2 sin 2x = + + = + + 2 . 4 π π 2 2 sin 2x 2 2 2 2 sin 2x − ≤ + ≤ ⇔ − + ≤ + + 2 ≤ 2 + 2 4 4
⇔ − 2 + 2 ≤ f ( x) ≤ 2 + 2 .
Giá trị lớn nhất của hàm số π π
f (x) bằng 2 + 2 khi sin 2x + = 1 ⇔ x = + kπ . 4 8
Giá trị nhỏ nhất của hàm số π π
f (x) bằng − 2 + 2 khi 3 sin 2x + = 1 − ⇔ x = − + kπ . 4 8
M + m = ( + )2 +( − )2 2 2 2 2 2 2 =12 .
Câu 16: [2] Cho phương trình 2 π 2 π
sin x sin 5x 2cos x 2cos 2x + = − − +
. Số vị trí biểu diễn các 4 4
nghiệm của phương trình trên đường tròn lượng giác là ? A. 1. B. 2 . C. 4 . D. 6 . Lời giải Chọn D 2 π π 2cos x 1 cos 2x − = + − = 1+ sin 2x 4 2 Ta có 2 π π 2cos + 2x =1+ cos + 4x =1− sin 4x 4 2
Do đó phương trình tương đương với sin x + sin 5x = sin 2x + sin 4x ⇔ 2sin 3 .
x cos 2x = 2sin 3 .xcos x kπ x = 3 sin 3x = 0 kπ k2π ⇔ ⇔
x = k2π ⇔ x = = (k ∈ )
cos 2x = cos x 3 6 k2π x = 3
Vậy có 6 điểm biểu diễn trên đường tròn lượng giác. x
Câu 17: [2] Cho hàm số f (x) 9 =
, x ∈ R . Nếu a + b = 3 thì f (a) + f (b − 2) có giá trị bằng 3+ 9x A. 1. B. 2 . C. 1 D. 3 . 4 4 Lời giải Chọn A
Ta có: b − 2 =1− a 9 a 1−a f (a) 9 =
f b − = f − a = = a ( ) ( ) 9 3 ; 2 1 1 3+ 9 3+ 9 −a 3+ 9a a
⇒ f (a) + f (b − ) 9 3 2 = + = 1 3+ 9a 3+ 9a
Câu 18: [3] Có bao nhiêu giá trị nguyên thuộc khoảng ( 9;
− 9) của tham số m để bất phương trình x ≤ ( 2 3log
2log m x − x − (1− x) 1− x ) có nghiệm thực? A. 6 . B. 7 . C. 10. D. 11. Lời giải Chọn B 0 < x < 1 0 < x <1 0 < x <1 Điều kiện ⇔ ⇔ (1− x) . 2 m x − x −
(1− x) 1− x > 0 m x − (1− x) > 0 m > > 0 x
Bất phương trình đã cho tương đương x ≤
(m x−x −( −x) −x)2 3 2 log log 1 1
⇔ x ≤ (m x − x −( − x) − x)2 3 2 1 1 ⇔ x x ≤ ( 2
m x − x − (1− x) 1− x )
x x + (1− x) 1− x x 1− x ⇔ m ≥ = + . 2 x − x 1− x x
Áp dụng bất đẳng thức cô si ta có x 1 1 − x x x + − + + ≥ 2 x + 2 1− x . 1− x x
Vì vậy m ≥ x + 1− x .
Khảo sát hàm số f (x) = x + 1− x trên (0; )
1 ta được f (x) ≥ 2 ≈1,414 .
Vậy m có thể nhận được các giá trị 2,3,4,5,6,7,8.
Câu 19: [3] Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26 . Bạn Hải rút ngẫu nhiên cùng một lúc
bốn tấm thẻ trong hộp . Hỏi có bao nhiêu cách rút bốn tấm thẻ sao cho bất kỳ hai trong bốn tấm
thẻ lấy ra đó có hai số tương ứng trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị? A. 2024. B. 8855. C. 7315. D. 10626. Lời giải Chọn B 10
Số cách rút 4 tấm thẻ trong 26 tấm thẻ sao cho bất kỳ hai trong bốn tấm thẻ lấy ra đó có hai số
tương ứng trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị bằng cách bỏ thêm 4 tấm thẻ vào
hàng ngang gồm 22 tấm thẻ sao cho hai tấm thẻ bỏ vào không kề nhau.
22 tấm thẻ kề nhau sinh ra 23 ô trống, nên số cách rút thẻ thẻ thoả mãn là: 4 C = 8855 (cách) 23
Câu 20: [2] Gọi A là tập hợp tất cả các số tự nhiên có tám chữ số. Chọn ngẫu nhiên một số thuộc A ,
tính xác suất để số tự nhiên được chọn chia hết cho 7 ?(Kết quả làm tròn đến hàng phần trăm) A. 0,17 . B. 0,14. C. 0,21. D. 0,12. Lời giải Chọn B
Gọi số có tám chữ số là a a ...a 1 2 8 Ta có: n(Ω) 7 = 9.10
Gọi biến cố B : “Số tự nhiên lấy được chia hết cho 7”
Khi đó: 10000004 ≤ a a ...a ≤ 99999998 1 2 8 n(B) =12857143
Vậy P(B) 12857143 = ≈ 0,14 7 9.10
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 6. Trong mỗi ý a),b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai. 2
Câu 1: Cho hàm số y = f (x) x + x −5 = . x + 3
a) Hàm số nghịch biến trên ( 7; − − 3) .
b) Đồ thị hàm số có đường tiệm cận xiên tạo với 2 trục tọa độ một tam giác có diện tích bằng 2 .
c) Có 15 giá trị nguyên của tham số p thuộc khoảng (0;20) để đồ thị hàm số số 2024 y = f (x) + p
có đúng ba đường tiệm cận.
d) Có 2022 giá trị nguyên của tham số m thuộc [ 2024 − ;2025] để hàm số
g (x) = f ( 2x − 2x − m) có 5 điểm cực trị. Lời giải a) b) c) d) S Đ S Đ
a) TXĐ: D = \{− } 3 . 2
x + x −5 ′ (2x + ) 1 (x + 3) 2 2
− x − x + 5 x + 6x +8 Ta có y′ = = = x + 3 (x +3)2 (x +3)2 2 x + 6x + 8 4 − < x < 3 − y′ = ⇒ y′ < 0 ⇔ (x +3)2 3 − < x < 2 −
Hàm số nghịch biến trên các khoảng ( 4; − − 3) và ( 4; − − 2). 11
Vậy mệnh đề a) là SAI. 2 + − b) x x 5 1 Ta có y = = x − 2 + . x + 3 x + 3 Khi đó y − (x − ) 1 lim 2 = lim = 0 ; y − (x − ) 1 lim 2 = lim = 0 . x→+∞ x→+∞ x + 3 x→−∞ x→−∞ x + 3
Vậy đồ thị có tiệm cận xiên d : y = x − 2.
Gọi A = d ∩Ox ⇒ A(2;0); B = d ∩Oy ⇒ B(0; 2 − ) . Vậy S = . OA ∆ B 2
Vậy mệnh đề b) là ĐÚNG. c)) Ta có 2024 lim = 0 và 2024 lim
= 0 với mọi giá trị của tham số p nên đồ thị hàm
x→+∞ f (x) + p
x→−∞ f (x) + p số 2024 y =
luôn có đường tiệm cận ngang y = 0 do đó để đồ thị hàm số 2024 y = có f (x) + p f (x) + p
đúng ba đường tiệm cận thì phương trình f (x) + p = 0 ⇔ f (x) = − p có hai nghiệm phân biệt. 2 x + 6x + 8 x = 2 − ⇒ f ( 2) − = 3 −
Ta có y′ = f ′(x) =
⇒ f ′ x = 0 ⇔ 2 ( ) (x +3) x = 4 − ⇒ f ( 4) − = 7 −
Căn cứ vào bảng biến thiên của hàm số đã cho suy ra phương trình trên có đúng hai nghiệm phân − p > 3 − ⇒ 0 < p < 3 biệt khi và chỉ khi
đồng thời p là một số nguyên nên ta tìm được tất cả
− p < 7 ⇒ 7 < p < 20 14giá trị thỏa mãn.
Vậy mệnh đề c) là mệnh đề SAI. 2 x + 6x + 8 x = 2 −
d) Do y′ = f ′(x) =
⇒ f ′ x = 0 ⇔ nên 2 ( ) (x +3) x = 4 − 2
x − 2x − m ≠ 3 − x =1 x g′(x) = = 2(x − ) 1 f ′( 1 2
x − 2x − m) ⇒ g′(x) 2 = 0 ⇔
⇔ x − 2x = m − 2 . 2 x 2x m 2 − − = − 2
x − 2x = m − 4 2
x − 2x − m = 4 − Xét h(x) 2
= x − 2x có bảng biến thiên
Để thỏa mãn thì m − 4 > 1 − ⇔ m > 3.
Do m nguyên thuộc [ 2024 −
;2025] nên có 2022 giá trị thỏa mãn Chọn ĐÚNG.
Câu 2: Trong không gian Oxyz , cho ba điểm A(0;0;− ) 1 , B( 1; − 1;0), C (1;0; ) 1 . − − a) Điểm 1 1 1
I( ; ; ) là trung điểm của đoạn thẳng AB . 2 2 2
b) Khi tứ giác ABCD là hình bình hành thì D O = 6 . 12 c) Điểm H ( ; a ;
b c) là chân đường cao kẻ từ A xuống cạnh BC của tam giác ABC . Khi đó 5
a + b + c = . 3
d) Biết điểm M ( ;
x y; z) để biểu thức 2 2 2
3MA + 2MB − MC đạt giá trị nhỏ nhất, khi đó
4x-2y+z = 2024 . Lời giải a) b) c) d) Đ S S S + − + − −
a) Toạ độ trung điểm 1
I của đoạn thẳng AB là 0 1 0 1 1 0 1 1 I − ; ; hay I ; ; . 2 2 2 2 2 2 Vậy a) đúng. b) Gọi D( ;
x y; z). Để tứ giác ABCD là hình bình hành thì 1 − = 1− x AB DC 1 =
⇒ = 0 − y ⇒ D(2;−1;0) ⇒ D O = 5. 1 =1− z Vậy b) sai.
c) Ta có BC = (2; 1; − 1). Gọi H ( ;
x y; z) là chân đường cao kẻ từ A xuống cạnh BC của tam giác ABC .
Suy ra BH = (x +1; y −1; z) . BH / /BC
x +1 = 2t; y −1 = t − ; z = t ( ) 1
Ta có ⇔ AH ⊥ BC AH ⋅ BC = 0 (2) ( )
1 ⇒ H (2t −1; t
− +1;t) ⇒ AH = (2t −1; t − +1;t +1) . ( − 2) 1
⇒ 2.(2t −1) − ( t
− +1) + t +1 = 0 ⇔ 6t = 2 ⇔ t = ⇒ 1 2 1 H( ; ; ) nên 2
a + b + c = . 3 3 3 3 3 Vậy c) sai. d)
AM = ( ;x y; z + ) 2 2 2 1
AM = x + y + (z + )2 1 M ( ; x y; z)
⇒ BM = (x +1; y −1; z) 2
⇒ BM = (x + )2 1 + ( y − )2 2 1 + z CM =
(x −1; y;z − ) 2 1 CM = (x − )2 2
1 + y + (z − )2 1 2 2 2
⇒ P = 3MA + 2MB − MC 2 2
= x + y + (z + )2 + (x + )2 + ( y − )2 2
+ z − (x − )2 2 3 1 2 1 1
1 + y + (z − )2 1 2 2 2 2 3 x y z x y z x = + + + − + + = + +
( y − )2 +( z + )2 9 9 4 4 4 6 4 8 5 2 2 1 2 2 − ≥ − . 2 4 4 9 ⇒ MinP = − 3 ⇔ x = − , 1 y = , z = 1 − , khi đó 3 1 M ; ; 1 − − . 4 4 2 4 2
Vậy P = 4x-2y + z = -3-1-1= -5. Vậy d) Sai.
Câu 3: Cho hình hộp chữ nhật ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh bằng a . Gọi M ,
N , P theo thứ tự là trung điểm của các cạnh A′B′ , CC′ , AD . Biết rằng BM và NP vuông góc với nhau. 13
a) Góc giữa hai đường thẳng AC và MP bằng 90° .
b) Khoảng cách giữa hai đường thẳng BP và MC′ bằng a 2 .
c) Nếu ϕ là góc giữa hai mặt phẳng (MNP) và ( ABCD) thì 3 cosϕ = . 3
d) Thể tích khối tứ diện AMNP bằng 1 3 a . 16 Lời giải Câu 3 a) b) c) d) Đ S Đ Đ A' D' M B' C' G N A P D B C a)
AC = AB + AD
MP = MA′ + A′A + AP Ta có
AC MP = ( AB + AD) 1 . BA + A A + AP ′ 2 1 2 1
= − AB + A . D BA + A .
B A' A + A .
D A′A + A . B AP + A . D AP 2 2 1 2 1 2 = − a + a = 0 2 2
Vậy góc giữa AC và MP bằng 90° .
MC′ ⊂ ( A′B C ′ D ′ ′)
b) Khẳng định sai, vì:
⇒ d (MC ,′ BP) = d ((BCD),( A′B C ′ D ′ ′)) = ′ ⊂ ( ) AA BP ABCD
Đặt AA′ = h . +) 1
BM = − AB + AA′ . 2
+) 1 1
PN = PD + DC + CN = AB + AD + AA′ . 2 2 +) 1 1 1
BM ⊥ PN ⇒ BM.PN = 0 ⇔ − AB + AA . AB + AD + AA ′ ′ = 0 2 2 2 14