Đề mẫu ôn tập - Toán cao cấp c2 | Trường Đại Học Duy Tân

Đề mẫu ôn tập - Toán cao cấp c2 | Trường Đại Học Duy Tân được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

7 4 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Toán cao cấp c2 (mth 102)

Trường: Đại học Duy Tân

Thông tin:

4 trang 1 tháng trước

Tác giả:

Profile Mai Nguyệt
Page of 1 4
ĐỀ Ẫ M U TOÁN CAO CẤP A2
Phầ ỏ ắ ện 1: Câu h i tr c nghi m ( ) mỗi câu đúng 0,2 điể ổng 4,0 điểm ; t m
1. T nh c a hàm s ập xác đị ủ ố
2 2 2
( , ) 9 16f x y x y x= − + − +
là:
A.
3,3 4,4D = − −
B.
9,9 16,16D = − −
C.
9,9 4,4D = − −
D.
3,3 16,16D = − −
2. Cho hàm s ố
3 2 3
( , ) 4 2 5f x y x xy y= + − +
. Đạo hàm riêng cấp 1 của hàm số
( , )f x y
theo bi n là: ế x
A.
2 2 2
( , ) 3 4 6
x
f x y x y y= + −
B.
C.
2
( , ) 8 6
x
f x y xy y= −
D.
3. Cho hàm s ố
4 2 3 4
( , ) 2 3 1f x y x x y xy y= − + +
. Ch n câu tr l ọ ả ời đúng:
A.
3 2
( , ) 4 4 3
xy
f x y x xy y= − +
B.
2
( , ) 12 4
xy
f x y x y= −
C.
2
( , ) 4 9
xy
f x y x y= − +
D.
2
( , ) 4 9
xy
f x y x y= − −
4. Cho hàm s ố
4 4
( , ) 4 1f x y x xy y= + + +
. Ch n câu tr l : ọ ả ời đúng
A. Hàm s m t i h n B. Hàm s m t i h n ố có 1 điể ớ ạ ố có 2 điể ớ ạ
C. Hàm s m t i h n D. Hàm s m t i h n ố không có điể ớ ạ ố có 3 điể ớ ạ
5. Cho hàm s ố
4 3
( , ) 4 3 1f x y x xy y= + + +
. Ch n câu tr ọ ả lười đúng:
A.
2
( , ) 4 9
y
f x y x y= +
B.
3 2
( , ) 4 4 9
y
f x y x x y= + +
C.
3
( , ) 4 4
y
f x y x y= +
D.
3 2
( , ) 4 4 9 1
y
f x y x x y= + + +
6. M t ph ng ti p xúc v hàm s ặ ẳ ế ới đồ thị ố
3 3
( , ) 3 1f x y x xy y= + − +
tại điểm
(0,1,2)M
có phương trình là:
A.
3 3 5z x y= − − +
B.
3 3 5z x y= − +
C.
3 3 5z x y= + +
D.
3 3 5z x y= − −
7. Bi u th hi n là m t hình ch nh t trong h t vuông góc ? ể ức nào sau đây thể ệ D ộ ữ ậ ệ ọa độ Oxy
A.
( )
, | 0 1;0 1D x y x y x= +
B.
( )
, | 0 1;0 1D x y y x y= +
C.
( )
, | 0 1;0 1D x y x y=
D.
( )
, | 0 1; 1 1D x y x x y x= − +
8. K t qu c a tích phân ế ả ủ
1 2
0 0
8I xydy dx
=
b ng: ằ
A. 2 B. 4 C. 6 D. 8
9. K t qu c a tích phân ế ả ủ
1 2 3
0 0 0
2I xdz dy d
=
b ng: ằ
Page of 2 4
A. 6 B. 4 C. 10 D. 8
10. Cho là mi n có d ), bi u th c bi u di n là: D ề ạng hình tam giác (như hình vẽ ể ứ ể ễ D
A.
( )
, |1 4;0D x y x y=
B.
( )
, |1 4;1D x y x y x=
C.
( )
, |1 4; 4D x y y y x= −
D.
( )
, |1 4;1 4D x y y x=
11. Bi u th hi n là m t kh i h p trong h t vuông góc ? ể ức nào sau đây thể ệ E ộ ố ộ ệ ọa độ Oxyz
A.
( )
, , | 0 1;0 ;1 3E x y z x y x z=
B.
( )
, , | 0 1;0 ; 3E x y z x y x y z= −
C.
( )
, , | 0 1;0 2;1 3E x y z x y z=
D.
( )
, , | 0 1;0 2;E x y z x y x y z x= − +
12. K t qu c a tích phân ế ả ủ
2
D
I xdA
=
, với
0,1 0, 2D =
là:
A. 1 B. 3 C. 5 D. 2
13. K t qu c a tích phân ế ả ủ
4
E
I xydV
=

, với
0,1 0,2 0,3E =
là:
A. 12 B. 10 C. 14 D. 21
14. ng tham s Cho đường cong (C) có phương trình dạ ố
1 3
,0 1
2 4
x t
t
y t
= +
= +
. K t qu c ng ế ả ủa tích phân đườ
( )
2
C
x y ds+
b ng: ằ
A. 42 B. 45 C. 54 D. 24
15. Cho đường cong (C) có phương trình dạng tham số
1 3
,0 1
2 4
x t
t
y t
= +
= +
. K t qu c ng ế ả ủa tích phân đườ
( )
2
C
x y dx+
b ng: ằ
Page of 3 4
A. 17 B. 18 C. 27 D. 28
16. Cho đường cong (C) có phương trình dạng tham số
1 3
,0 1
2 4
x t
t
y t
= +
= +
. K t qu c ng ế ả ủa tích phân đườ
( )
2
C
x y dy+
b ng: ằ
A. 16 B. 26 C. 6 D. 36
17. Trường vector nào sau đây bảo toàn?
A.
( ) ( )
2 7
( , ) 7 7F x y x y i x y= + + +
B.
( ) ( )
2 7
( , ) 7F x y x y i x y= + + +
C.
( ) ( )
2 7
( , ) 7 7F x y x y i x y= − + −
D.
( ) ( )
2 7
( , ) 7 7F x y x y i x y= − + +
18. Gradient c a hàm s ủ ố
2
( , , )f x y z x y= +
b ng: ằ
A.
( , , ) 2f x y z xi yj z = + +
B.
( , , ) 2f x y z xi zj y = + +
C.
( , , )f x y z xi yj z = + +
D.
( , , )f x y z xi zj y = + +
19. Cho hàm s ố
( , ) 2 1f x y x y= + +
ng vector và đường cong (C) có phương trình dạ
( )
( ) 1 2r t t i t= + +
,
0 1t
. Ch n câu tr l ọ ả ời đúng:
A.
4
C
f dr = −
B.
5
C
f dr =
C.
5
C
f dr = −
D.
4
C
f dr =
20. Công ng vector y d cho b i m t hàm vecto ( ), sinh ra khi cho trườ F chạ ọc đường cong trơn C ở ộ r t
a t b
được xác đị ức nào sau đây?nh bằng công th
A.
( )
'
b
C a
d t dt =
F r r
B.
( )
( )
( )
b
C a
d t t dt =
F r F r r
C.
( )
( )
b
C a
d t dt =
F r F r
D.
( )
( )
( )
'
b
C a
d t t dt =
F r F r r
Phầ ỏ ả ờ ắn 2: Câu h i tr l i ng n ( ) mỗi câu đúng 0,5 điể ổng 3,0 điểm ; t m
1. Cho hàm s ố
3 2 3
( , ) 3f x y x x y= − +
. Tính
(0,1)
xy
f
?
2. Tính tích phân
2
D
I ydA
=
, v là mi c g i h n b nh là ới D ền đượ ớ ạ ởi tam giác có 3 đỉ
( ) ( ) ( )
0,0 ; 0,1 ; 1,1
.
3. Tính tích phân
6
E
I xyzdV
=

, với
0,1 0,2 0,3E =
.
4. S d ng nh lý Green ử ụ đị t ng : ính tích phân đườ
(sin 2022 ) (5 2023 )
x y
C
I y dx x dy= − + +
với
( )C
là
đường tròn
2 2
9x y+ =
.
5. Tích tích phân m t ặ
S
y dS
trong đó S là mặt 𝑧 = 3𝑥 + 4𝑦; 0 ≤ 𝑥 ≤ 1; 0 ≤ 𝑦 ≤ 2.
Page of 4 4
6. M t ch m chuy n th ng t ộ ất điể ển động trên đoạ ẳ ừ
(1,2)A
n đế
(4,3)B
i tác d ng c ng ldướ ụ ủa trườ ực
( , ) ( ) (2 5)F x y x y i x= + + +
. Tính công sinh ra.
Phầ ỏ ự ận 3: Câu h i t lu n ( ) tổng 3,0 điểm
1. Tính tích phân (1,5 điểm)
2
10
D
I x ydA
=
, v . ới 𝐷 =
{(
𝑥, 𝑦
)|
0 ≤ 𝑥 ≤ 1; 0 ≤ 𝑦 ≤ 2𝑥
}
2. Tìm c c tr (1,5 điểm) ự ị địa phương và điểm yên ngựa (nếu có) của hàm số sau:
2 5
( , ) 2 405f x y x y x y= + − −
.
------------------------------- H ------------------------------- ẾT
Ghi chú : + Sinh viên ch c phép s d ng tài li i tích Calculus 7e tỉ đượ ử ụ ệu là sách in “Giả ập 2” c a tác gi ủ ả
James Stewart, nhóm biên d ch c i h c Duy Tân. ị ủa Trường Đạ ọ
+ Cán b coi thi không gi i thích gì thêm. ộ ả
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ MẪU TOÁN CAO CẤP A2
Phần 1: Câu hỏi trắc nghiệm (mỗi câu đúng 0,2 điểm ; tổng 4,0 điểm)
1. Tập xác định của hàm s ố 2 2 2 (f ,x )y =9 x − +16 −y + x là: A. D = 3, −  3  4, − 4 B. D = 9, −  9  16 − ,  16 C. D = 9, −  9  4 − , 4 D. D = 3, −  3  16, −  16 2. Cho hàm s ố 3 2 3 (f ,x )y =x 4+ xy 2 − y 5
+. Đạo hàm riêng cấp 1 của hàm sốf ( , x )y theo biến là: x A. 2 2 2 f (x , ) y 3 = x 4 + y 6 − y B. 2 2 f (x , ) y 3 = x +4 y x x C. 2 f (x , ) y 8 = xy 6 − y D. 2 2 f (x , ) y 3 = x 4 − y x x 3. Cho hàm s ố 4 2 3 4 (f ,x )y x = 2− x 3 y + xy + y 1. Ch n câu tr ọ ả lời đúng: A. 3 2 f (x , y) 4 = x 4 − xy +3y B. 2 f (x , ) y 12 = x −4 y xy xy C. 2 f (x , ) y = 4 − x +9y D. 2 f ( x , ) y = 4 − x 9 − y xy xy 4. Cho hàm s ố 4 4 (f , x )y =x 4 + xy + y 1+. Ch n câu tr ọ ả lời đúng: A. Hàm s ố có 1 điểm tới hạn B. Hàm s ố có 2 điểm tới hạn C. Hàm s
ố không có điểm tới hạn D. Hàm s ố có 3 điểm tới hạn 5. Cho hàm s ố 4 3
(f ,x )y =x 4+ xy 3+ y 1+. Ch n câu tr ọ ả lười đúng: A. 2 f ( x , ) y 4 = x 9 + y B. 3 2 f ( x , ) y 4 = x 4 + x 9 + y y y C. 3 f ( x , ) y 4 = x +4 y D. 3 2 f ( x , ) y 4 = x 4 + x 9 + y 1 + y y
6. Mặt phẳng tiếp xúc với đồ thị hàm s ố 3 3 (f ,
x )y =x 3+ xy − y 1+ tại điểm (
M 0,1,2) có phương trình là: A. z 3 = − x 3 − y 5 + B. z 3= x 3 − y 5 + C. z 3= x 3 + y 5 + D. z 3= x 3 − y 5 −
7. Biểu thức nào sau đây thể hiện D là m t hình ch ộ
ữ nhật trong hệ tọa độ vuông góc Oxy? A. D (
= ,x ) |y 0 x 1;0  y  x1+ B. D (
= ,x ) |y 0 y 1;0 x  y1+ C. D (
= ,x ) |y 0 x 1;0  y1 D. D (
= ,x ) |y 0 x 1; x 1−  y  x1+ 1 2  
8. Kết quả của tích phân I = 8xydy dx    bằng: 0  0  A. 2 B. 4 C. 6 D. 8 1 2 3    
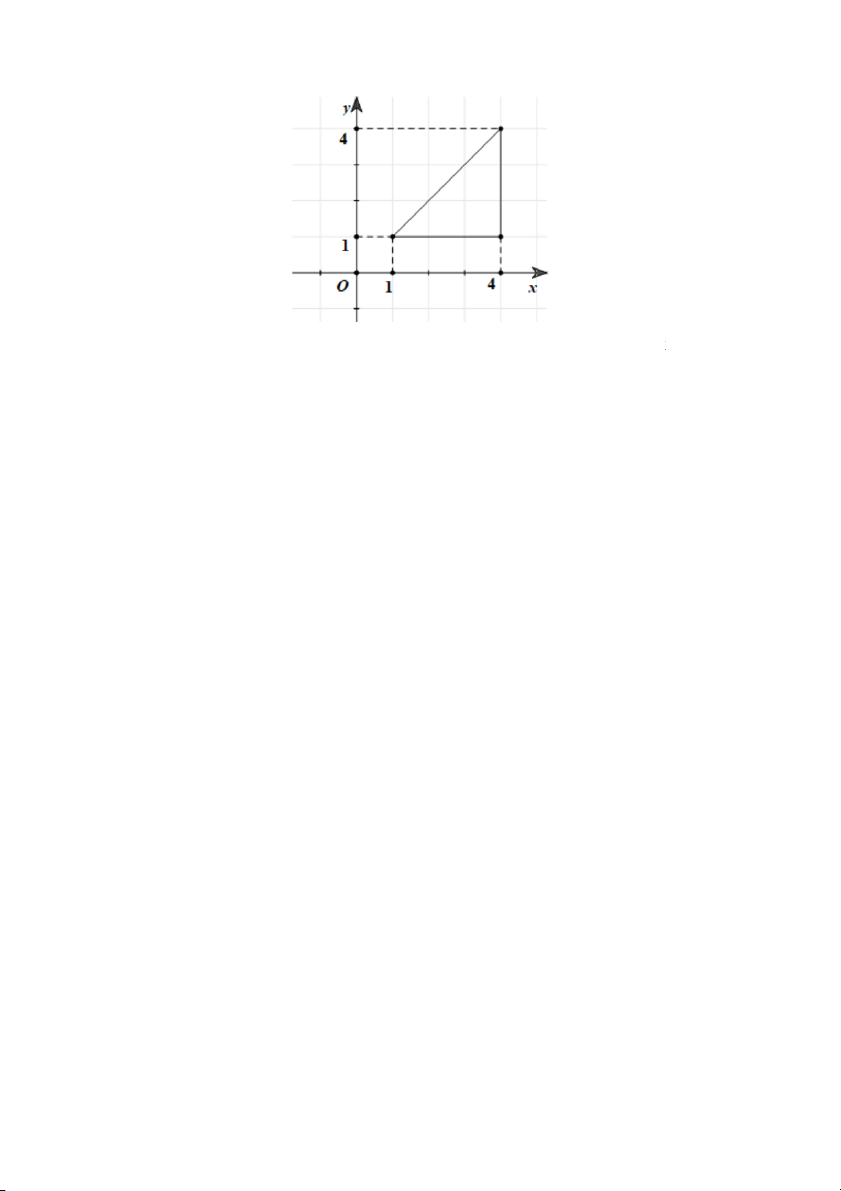
9. Kết quả của tích phân I = 2xdz dy d      bằng: 0  0 0   Page 1 of 4 A. 6 B. 4 C. 10 D. 8 10. Cho D là miền có d ), bi
ạng hình tam giác (như hình vẽ ểu th c bi ứ ểu diễn D là: A. D (
= ,x ) |y1 x 4;0  y  B. D (
= ,x ) |y1 x 4;1  y x C. D (
= ,x ) |y1 y 4; −y  x 4 D. D (
= ,x ) |y1  y 4;1  x 4
11. Biểu thức nào sau đây thể hiện là m E t kh ộ i h ố p trong h ộ
ệ tọa độ vuông góc Oxyz? A. E ( ,x = , )y | 0 z  1 x ;0  y ;1 x  3 z B. E ( ,x = ,y) |z 0 x 1;0  y ;x  y −  3 z C. E( ,=x, )y | 0 z  1 x ;0   2 y ;1   3 z D. E ( , =x ,y) |z 0 x  1;0  y  2; x −y z   x +
12. Kết quả của tích phân I = 2 xdA  , với D 0, = 1 0, 2 là: D A. 1 B. 3 C. 5 D. 2
13. Kết quả của tích phân I = 4 xydV  , với E 0, =  1  0,2   0,3 là: E A. 12 B. 10 C. 14 D. 21 x = 1+ 3t
14.Cho đường cong (C) có phương trình dạng tham s ố ,0 
 t  1. Kết quả của tích phân đường y = 2 + 4t  (2x y +  ) ds bằng: C A. 42 B. 45 C. 54 D. 24 x = 1+ 3t
15. Cho đường cong (C) có phương trình dạng tham số ,0 
 t  1. Kết quả của tích phân đường y = 2 + 4t  (2x y +  ) dx bằng: C Page 2 of 4 A. 17 B. 18 C. 27 D. 28 x = 1+ 3t
16. Cho đường cong (C) có phương trình dạng tham số ,0 
 t  1. Kết quả của tích phân đường y  = 2 + 4t (2x y +  ) dy bằng: C A. 16 B. 26 C. 6 D. 36
17. Trường vector nào sau đây bảo toàn? A. F x y ( 2 = x + )y i( 7 ( , ) 7 +7 x + )y B. F x y ( 2 = x + )y i ( 7 ( , ) 7 + x + )y C. F x y ( 2 = x − )y i( 7 ( , ) 7 7 + x − )y D. F x y ( 2 = x − )y i ( 7 ( , ) 7 7 + x + )y 18. Gradient của hàm s ố 2 (f , x , y )z =x +y bằng: A. (f , x , y )z 2 = xi +yj +z B. (f , x , y )z 2 = xi +zj + y C. (f , x , y )z =xi +yj +z D. (f , x , y )z =xi +zj + y 19. Cho hàm số (f , x )y = x 2 + y 1 + ng vector
và đường cong (C) có phương trình dạ (r )t (= 1 ) + t i +2 t, 0  t 1. Ch n câu tr ọ ả lời đúng: A. f   dr = 4 −  B. f   dr 5 =  C. f   dr = 5 −  D. f   dr 4 =  C C C C
20. Công sinh ra khi cho trường vector F chạy dọc đường cong trơn C cho bởi m t hàm vecto ộ ( r t a ),  t  b
được xác định bằng công thức nào sau đây? A. b F d r = 'r (t) dt   B. b
F dr = F ( (r )t) r ( t) dt   C a C a C. b F dr = F ( r(t)) dt   D. b
F dr = F( (r t)) r '( t) dt   C a C a
Phần 2: Câu hỏi trả ờ l ắ
i ng n (mỗi câu đúng 0,5 điểm ; tổng 3,0 điểm) 1. Cho hàm s ố 3 2 3 (f , x )y x = 3− x y +. Tính f (0,1)? xy 2. Tính tích phân I = 2 ydA  , với D là mi c g ền đượ ới hạn b nh là ởi tam giác có 3 đỉ (0,0);(0, )1 (; 1),1. D
3. Tính tích phân I = 6 xyzdV  , với E  0,
= 1  0,2   0,3. E 4. S d
ử ụng định lý Green tính tích phân đường I: = (sin 2022 x y − )dx + (5x + 202y3 )dy  với (C) là C đường tròn 2 2 x + y =9.
5. Tích tích phân mặt y dS 
trong đó S là mặt 𝑧 = 3𝑥 + 4𝑦; 0 ≤ 𝑥 ≤ 1; 0 ≤ 𝑦 ≤ 2. S Page 3 of 4 6. M t ch ộ m chuy ất điể n th ển động trên đoạ ẳng từ ( A1,2) đến ( B 4,3) dưới tác d ng c ụ ủa trường lực ( F , x ) y (= x + )y i (2 + x 5 + ) . Tính công sinh ra.
Phần 3: Câu hỏi tự luận (tổng 3,0 điểm)
1. (1,5 điểm) Tính tích phân 2 I = 10x ydA 
, với 𝐷 = {(𝑥, 𝑦)|0 ≤ 𝑥 ≤ 1; 0 ≤ 𝑦 ≤ 2𝑥}. D
2. (1,5 điểm) Tìm cực trị địa phương và điểm yên ngựa (nếu có) của hàm số sau: 2 5 (f ,x )y =x +y 2− x40 − 5 y .
------------------------------- HẾT -------------------------------
Ghi chú : + Sinh viên chỉ c phép s đượ
ử dụng tài liệu là sách in “Giải tích Calculus 7e t
ập 2” của tác gi ả
James Stewart, nhóm biên dịch của Trường Đại h c Duy ọ Tân. + Cán b coi thi không gi ộ i thích gì thêm. ả Page 4 of 4