











Preview text:
lOMoARcPSD|45315597 lOMoARcPSD|45315597
TRƯỜNG ĐH KIẾN TRÚC HÀ NỘI
KỲ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN NĂM HỌC 2020-2021 ĐỀ MINH HỌA
Môn: Xác Suất Thống Kê
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Mã đề thi 001
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:.....................................................................
Lớp: .............................
Câu 1: Một lô hàng gồm 100 sản phẩm trong đó có 95 sản phẩm đạt tiêu chuẩn và còn lại là các sản
phẩm không đạt tiêu chuẩn. Xác suất để lấy được một sản phẩm không đạt tiêu chuẩn từ lô hàng bằng A. 0,05 B. 0,5 C. 0,95 D. 0,095
Câu 2: Cho A, B là hai biến cố của một phép thử ngẫu nhiên nào đó. Biết rằng P(A)=0,4; P(B)=0,2 và
P(AB)=0,1 Giá trị của P(A+B) là A. 0,6 B. 0,5 C. 0,7 D. 0,4
Câu 3: Tung một con xúc xắc đồng chất hai lần liên tiếp. Xác suất để tung được cả hai lần đều ra mặt 6 chấm là 1 1 1 1 A. B. C. D. 12 6 36 13
Câu 4: Tung một con xúc x ắc đông chất 8 lần liên tiếp. Gọi X là số lần xuất hiện mặt có số chấm bằng 5. Tập
giá trị của X là A. 1, 2,3, 4,5, 6, 7,8 B.0,1, 2,3, 4,5, 6, 7 C. 0,1, 2,3, 4, 6, 7,8
D.0,1, 2,3, 4,5, 6, 7,8
Câu 5: Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau x x x X 1 2 3 P(X=x) 0,4 0,1 0,5
Phương sai của X bằng
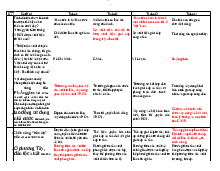
A. 0, 4.( x1 ) 2 0,1.( x2 ) 2 0, 5.( x3 ) 2 0, 4. x1 0,1. x2 0, 5.x32
0, 4. x1 0,1. x2 0, 5. 2 0, 4.( 2 2 2 B. x3 x1 )
0,1.( x2 ) 0, 5.( x3 )
C. (0, 4) 2 . x1 (0,1) 2 . x2 (0, 5) 2 . x3 0, 4. x1 0,1. x2 0, 5.x32
D. 0, 4. x1 0,1. x2 0, 5. x32 (0, 4) 2 . x1 (0,1) 2 . x2 (0, 5) 2.x3
Câu 6: Cho X là một biến ngẫu nhiên liên tục có hàm mật xác suất được cho như sau lOMoARcPSD|45315597 2 ( x[0,1] 3 x ) . f ( x) 0 ( x[0,1])
Kỳ vọng của X bằng 1 1
A. x.(3x 2 )dx
B. x.(3 x 2)dx C. 3x 2dx D. 3x 2dx 0 0
Câu 7: Cho biến ngẫu nhiên X
N (2;0, 04) . Ký hiệu EX, DX lần lượt là kỳ vọng và phương sai của X. Khi đó,
kỳ vọng và phương sai của X bằng
A. EX=2 và DX không xác định được
B. EX không xác định được và DX=0,04 C. EX=2 và DX=0,04
D. Cả EX và DX đều không xác định được
Câu 8: Tìm hiểu ngẫu nhiên 200 cây được một năm tuổi của giống cây T, thấy có 60 cây đượ c một năm không
đạt tiêu chuẩn. Với độ tin cậy 95%, khoảng tin cậy đối xứng theo tỷ lệ ( p ) các cây được một năm tuổi của
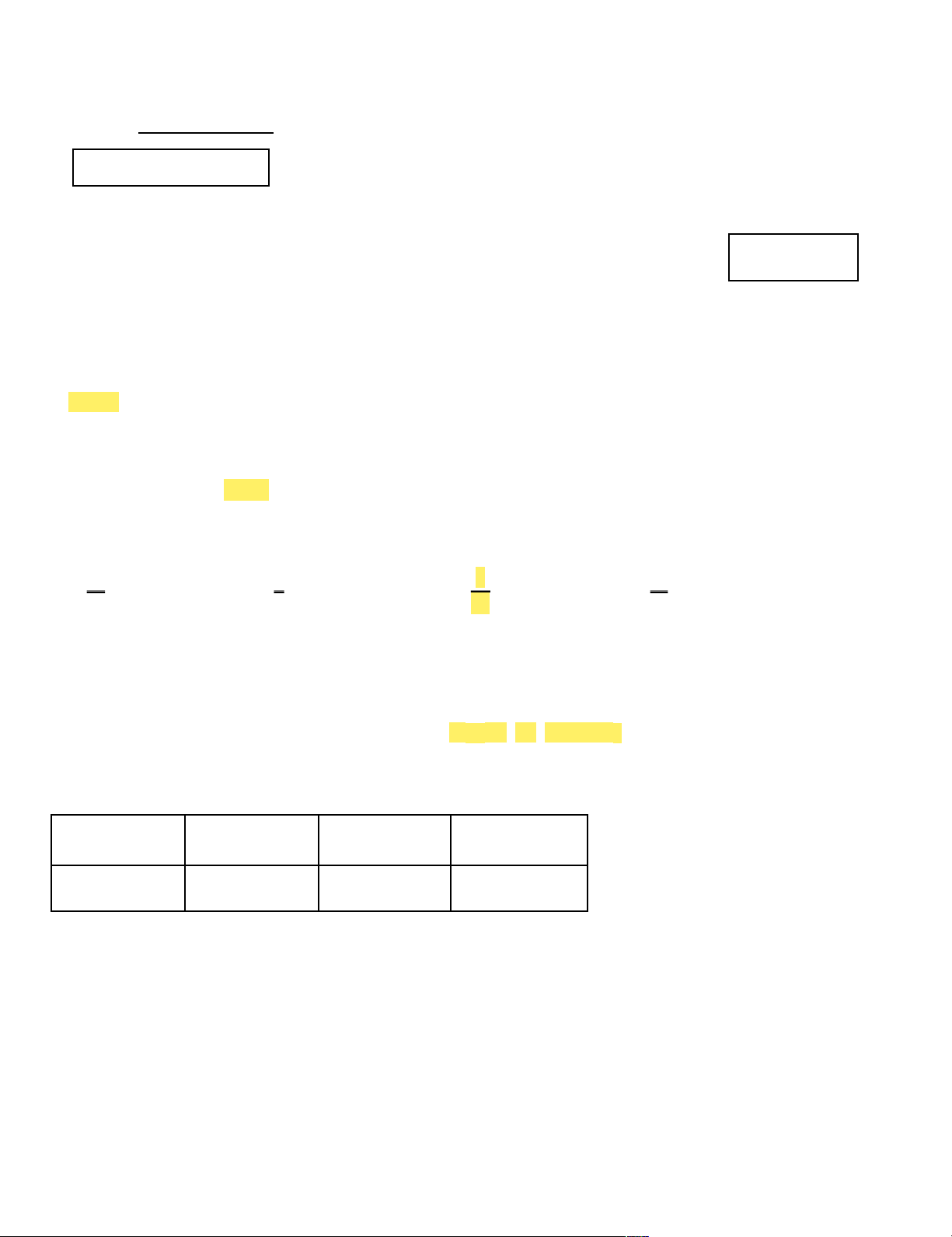
giống cây T không đạt tiêu chuẩn là? Biết rằng (1,96) và (1,645) 0,95 . 0,975 0, 3.0, 7 0, 3.0, 7 0,3.0,7 0,3.0,7 A. 0,31,96.
p 0, 31, 96. B. 0,31,645.
p 0, 31, 645. 200 200 200 200 0, 3.0, 7 0, 3.0, 7 0,3.0,7 0,3.0,7 C. 0, 3 1, 645.
p 0, 31, 645. D. 0,31,96.
p 0, 31, 96. 200 200 200 200
Câu 9: Cho X là biến ngẫu nhiên có phân phối chuẩn. Thực hiện một mẫu ngẫu nhiên cỡ n 30 quan sát về X
và thu được kỳ vọng của mẫu bằngx
và phương sai mẫu hiệu chỉnh bằng (s ')
. Công thức ước lượng 2
khoảng tin cậy đối xứng (với độ tin cậy 1 ) cho kỳ vọng của biến ngẫu nhiên X (với phương sai của X chưa biết ) là: s ' ; x s ' ; x s ' A. x T . T B. T ( n1) ( n1) ( n1) . 1( /2) 1( /2) . 1( /2) n n n C. x T . s ' D. ( ( n ;) 1) ; 1( /2) n
Câu 10: Đo ngẫu nhiên chiều cao (đơn vị: mét) của 10 cây được hai năm tuổi của giống cây X và thu được
các số liệu: 2; 2,2; 2,2; 2; 2,4; 2; 2; 2,2; 2,2 và 2,4. Tỷ lệ các cây được hai năm tuổi trong mẫu có chiều cao
lớn hơn kỳ vọng của mẫu là A. 40% B. 60% C. 20% D. 80%
Câu 11: Cân ngẫu nhiên 9 bao gạo do một đại lý cung ứng và thu được trong lượng (đơn vị: kg) của các bao
như sau: 50; 49,8; 50; 49,7; 50,1; 49,8; 50; 49,8 và 49,7. Kỳ vọng của mẫu đã cho bằng: A. 49,8778 (kg) B. 49,8779 (kg)
C. Xấp xỉ 49,8778 (kg)
D. Xấp xỉ 49,8779 (kg)
Câu 12: Một nhà máy tuyên bố rằng tỷ lệ sản phẩm không đạt tiêu chuẩn do họ sản suất ra luôn bằng 3%.
Người ta nghi ngờ rằng tỷ lệ này phải lớn hơn. Họ tiến hành kiểm tra ngẫu nhiên một số lượng lớn các sản
phẩm do nhà máy này sản xuất và thấy tỷ lệ sản phẩm được kiểm tra không đạt tiêu chuẩn bằng 4%. Gọi p là tỷ lệ
sản phẩm không đạt tiêu chuẩn do nhà máy sản xuất. Giả thuyết không (ký hiệu H 0 ) và đối giả thuyết (ký
hiệu H ) cho tỷ lệ sản phẩm không đạt tiêu chuẩn do nhà máy sản xuất là lOMoARcPSD|45315597 : p 0,
H : p 0, 04
H : p 0, 03
H : p 0, 04 H 03 0 0 0 0 A. B. C. D. : p 0,
H : p 0, 04
H : p 0, 03
H : p 0, 04 H 03
Câu 13: Một chuyên gia lai tạo giống cây trồng giống lúa than cao chống lụt vừa được lai tạo có chiều cao
trung bình là a (cm). Người ta cần kiểm định lại tuyên bố này. Họ chọn ngẫu nhiên n cây đo thử, với n 100 ,
thì được chiều cao trung bình bằng
x cm và phương sai mẫu hiệu chỉnh bằng (s ')
2. Giá trị của tiêu chuẩn kiểm
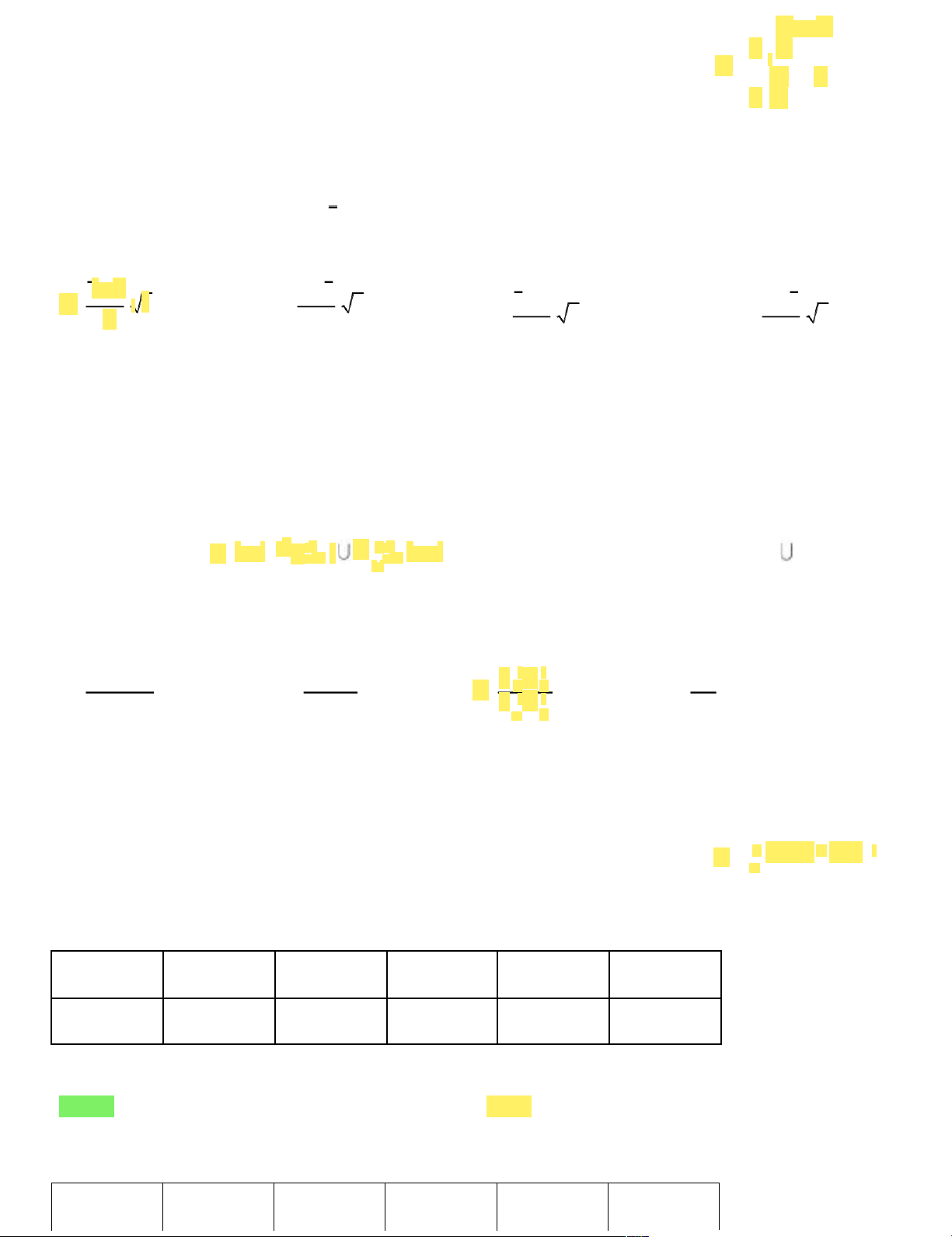
định (hoặc tiêu chuẩn thống kê) để tiến hành kiểm định bằng x a a x x a A. a x . n B. . n C. D. s ' s ' . n . n ( s ') 2 ( s ') 2
Câu 14: Chiều cao (đơn vị: mét) của một loại cây T được 1 năm tuổi là một biến ngẫu nhiên có phân phối
chuẩn. Theo số liệu cũ ghi lại, chiều cao trung bình của loại cây T được 1 năm tuổi là a mét. Các nhà nghiên
cứu nghi ngờ rằng số liệu này không còn đúng. Họ khảo sát đo đạc ngẫu nhiên n cây được 1 năm tuổi, với
n 30 và sử dụng giá trị của mức ý nghĩa bằng để trả lời câu hỏi nghi ngờ của họ. Khi đó, miền bác bỏ để
tiến hành kiểm định là khoảng ) (T ;) ) (T ;)
A. ( ; T ( n1)
B. (; T ( n1) 1) ; ) C. ( n1)
D. ( ; T ( n1) ( n1) 1 1 ( /2) ) (T ( n /2) 1 1 1 1 (
Câu 15: Thùng trái cây 1 gồm 25 quả loại I và 5 quả loại II. Thùng trái cây 2 gồm 26 quả loại I và 3 quả
loại II. Lấy ngẫu nhiên đồng thời mỗi thùng trái cây 2 quả. Xác suất để lấy được 4 quả loại I bằng C 2 C 2 C 4 C 2.C 2 C 4 A. C 25 25 26 C26 B. 51 C. D. 51 2 2 C 2 .C2 C 2.C 2 C 4 30 29 30 29 30 29 59
Câu 16: Tỷ lệ nảy mầm của loại hạt giống X là 95%. Người ta đem ngẫu nhiên 50 hạt của loại hat giống X đi
ươm một cách độc lập nhau và trong cùng điều kiện hoàn cảnh. Xác suất để có đúng 45 hạt nảy mầm trong số
50 hạt được ươm bằng: A. (0,95)45 .(0,5)5
B. C45 .[(0,95) 45 (0,5) 5 ] C. (0,95)45 (
D. C 45 .(0,95)45 .(0,5) 5 50 0,5) 50 5
Câu 17: Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau X -1 0 0,5 1 2 P(X=x) 0,2 0,4 0,1 0,2 0,1
Giá trị trung bình của X bằng A. 0,25 B. 2,5 C. 0,5 D. 0,7
Câu 18: Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau X -1 0 0,5 1,5 2 lOMoARcPSD|45315597 P(X=x) 0,2 0,1 0,3 0,2 0,2
Gọi F(x) là hàm phân phối xác suất của X. Khi đó, giá trị của F(0) bằng A. 0,3 B. 0,2 C. 0,1
D. Không xác định được
Câu 19: Biến ngẫu nhiên liên tục X có hàm mật độ xác suất được cho bởi 0 ( x[0, 3])
f ( x) 2 ( x[0,
( k là tham số). k . x 3])
Khi đó, giá trị của k bằng 1 1 1 1 A. B. C. D. 3 81 9 27
Câu 20: Biến ngẫu nhiên liên tục X có hàm mật độ xác suất được cho bởi 3x 2 x (x[0,1])
f (x) 2 0 (x[0,1])
Hàm nào dưới đây là hàm phân phối xác suất của X? 0 (x 0) 0 (x 0) A.
F (x) 3x
F (x) x x 2 3 B. 3 x 2 (x 0) (x 0) 2 2 0 ( x 0) 0 ( x 0) x 2 x 3 3x D. F ( x 3 F ( (0 x 2 (0 x C. ) x ) 1) x 1) 2 2 1 ( x 1) 1 ( x 1)
Câu 21: Chiều cao (đơn vị: cm) của một loài cây trồng được một 1 tháng tuổi là biến ngẫu nhiên liên tục X có phân
phối chuẩn. Biết rằng chiều cao trung bình và độ lệch chuẩn về chiều cao của loài cây trồng được 1 tháng tuổi này
lần lượt bằng 40 cm và 0,2 cm.Khi đó, xác suất để X nhận các giá trị trong khoảng (40,1; 40,5) bằng A. (2,5)(0,5 B. (40,5)(40,1) C. (0,5) (0
D.(12,5)(2,5) ) ,1)
Câu 22: Trọng lượng (đơn vị: kg) của một loại gia súc T là một biến ngẫu nhiên X có phân phối chuẩn. Biết rằng
trọng lượng trung bình của loại gia súc này bằng EX và phương sai của X bằng 0,36. Cân ngẫu nhiên 25 con gia
súc T, người ta thu được kỳ vọng của mẫu bằng 20 kg và đô lệch mẫu hiệu chỉnh bằng 0,3 kg. Biết rằng
(2,326) 0,99 và (2,576) 0,995 . Với độ tin cậy 99%, khoảng tin cậy đối xứng cho kỳ vọng của X bằng.
A. EX(19,84544; 20,15456)
B. EX(19,69088; 20,30912)
C. EX(19,814528; 20,185472)
D. EX(19,953632;20,046368) lOMoARcPSD|45315597
Câu 23: Tuổi thọ (đơn vị: tháng) của một loài côn trùng T là một biến ngẫu nhiên X có phân phối chuẩn và
bình phương độ lệch chuẩn bằng 0,04. Các chuyên gia khảo sát ngẫu nhiên 100 con côn trùng T và thu được
tháng. Biết rằng (1,96)
tuổi thọ trung bình bằng 12,5 tháng và độ lệch mẫu hiệu chỉnh bằng 0,25 0,975 , (1,645) 0,95
. Với độ tin cậy 95%, độ dài của khoảng ước lượng tin cậy đối xứng cho tuổi thọ trung bình
của loài côn trùng T là: A. 0, 0392 (tháng) B. 0,049 (tháng) C. 0,0784 (tháng) D. 0,098 (tháng)
Câu 24: Cân ngẫu nhiên 100 con gà thịt thuộc giống gà T và thu được bảng số liệu sau: Trọng lượng (kg) 1,5 1,6 1,7 1,8 1,9 2,0 2,1 Số con gà 5 10 10 30 25 15 5
Biết rằng (1,96) 0,975 , (1,645)
và một con gà thịt được gọi là đạt chuẩn nếu trọng lượng của nó 0,95
lớn hơn 1,75 kg. Với độ tin cậy 95%, khoảng tin cậy đối xứng cho tỷ lệ gà thịt đạt chuẩn bằng. A. (0,75; 0,83487) B. (0,71325; 0,78675) C. (0,66513; 0,83487) D. (0,66513; 0,75)
Câu 25: Một công ty B tuyên bố rằng có 60% hộ gia đình trong khu vực A thích sử dụng sản phẩm của họ. Một
đối thủ cạnh tranh nghi ngờ tuyên bố này và nghĩ rằng tỷ lệ này là thấp hơn. Để kiểm chứng nghi ngờ của mình,
đối thủ cạnh tranh này đã sử dụng mức ý nghĩa 5% và dựa thông tin điều tra ngẫu nhiên 400 hộ trong
khu vực A. Biết rằng tỷ lệ hộ gia đình thích sử dụng sản phẩm của công ty B trong mẫu điều tra là 55% và
(1,96) 0,975 , (1,645) 0,95 . Gọi p là tỷ lệ hộ gia đình trong khu vực A thích sử dụng sản phẩm
củacông ty B. Khi đó, giả thuyết không H 0 , đối giả thuyết H và miền bác bỏ W để tiến hành kiểm định được xác định như sau: : p 0, : p 0, H 6
và W (;1,645) B. . H 55
và W (;1,645) 0 A. 0 : p 0, : p 0, H 6 H 55 : p 0, : p 0, H 55
và W (;1,645) H 6
và W (;1,645) 0 C. 0 D. : p 0, : p 0, H 55 H 6
Câu 26: Tuổi thọ (đơn vị: tháng) của một loại pin do nhà máy A sản xu ất là một biến ngẫu nhiên X có phân
phối chuẩn với kỳ vọng là và độ lệch chuẩn là 0,2. Theo một số liệu cũ do nhà máy A cung cấp, tuổi thọ
trung bình của loại pin này là 15 tháng. Các chuyên gia nghi ngờ rằng số liệu này không còn đúng và nghĩ rằng
tuổi thọ trung bình của loại pin này đã thấp hơn. Để kiểm chứng nghi ngờ này, các chuyên gia đã sử dụng mức
ý nghĩa 5% và dựa vào thông tin khảo sát ngẫu nhiên 25 quả pin. Biết rằng mẫu khảo sát có tuổi thọ trung bình
bằng 14,5 tháng, độ lệch mẫu hiệu chỉnh bằng 0,3 và (1,96) ,(1,645) 0,975 0,95
. Giá trị của tiêu chuẩn
kiểm định (ký hiệu bởi tqs ) và miền bác bỏ W để tiến hành kiểm được 14,51
A. t qs 14,515. 25 và W= (;1, 645) B. t 5
. 25 và W= (;1, 645) qs 0, 2 0, 3 1514, C. t 5 .25 và W= (;1,96)
D. t 1514,5 . 25 và W= (;1,96) qs qs 0, 2 0, 3 lOMoARcPSD|45315597
Câu 27: Thời gian sử dụng (đơn vị: tháng) của một loại sản phẩm do nhà máy A sản xuất là một biến ngẫu
nhiên X có phân phối chuẩn với kỳ vọng là . Nhà máy A tuyên bố rằng sản phẩm này có thời gian sử dụng
trung bình là 4 tháng. Một người tiêu dùng nghi ngờ về tuyên bố này. Để kiểm chứng nghi ngờ này, người tiêu
dùng đã sử dụng mức ý nghĩa 1% và dựa vào thông tin khảo sát ngẫu nhiên 25 sản phẩm. Biết rằng mẫu khảo
sát có thời gian sử dụng trung bình bằng 4,8 tháng, độ lệch mẫu hiệu chỉnh bằng 0,2, T ( 24) 2, 797 và 0,995 T ( 24) 2, 492
. Giá trị của tiêu chuẩn kiểm định (ký hiệu bởi t
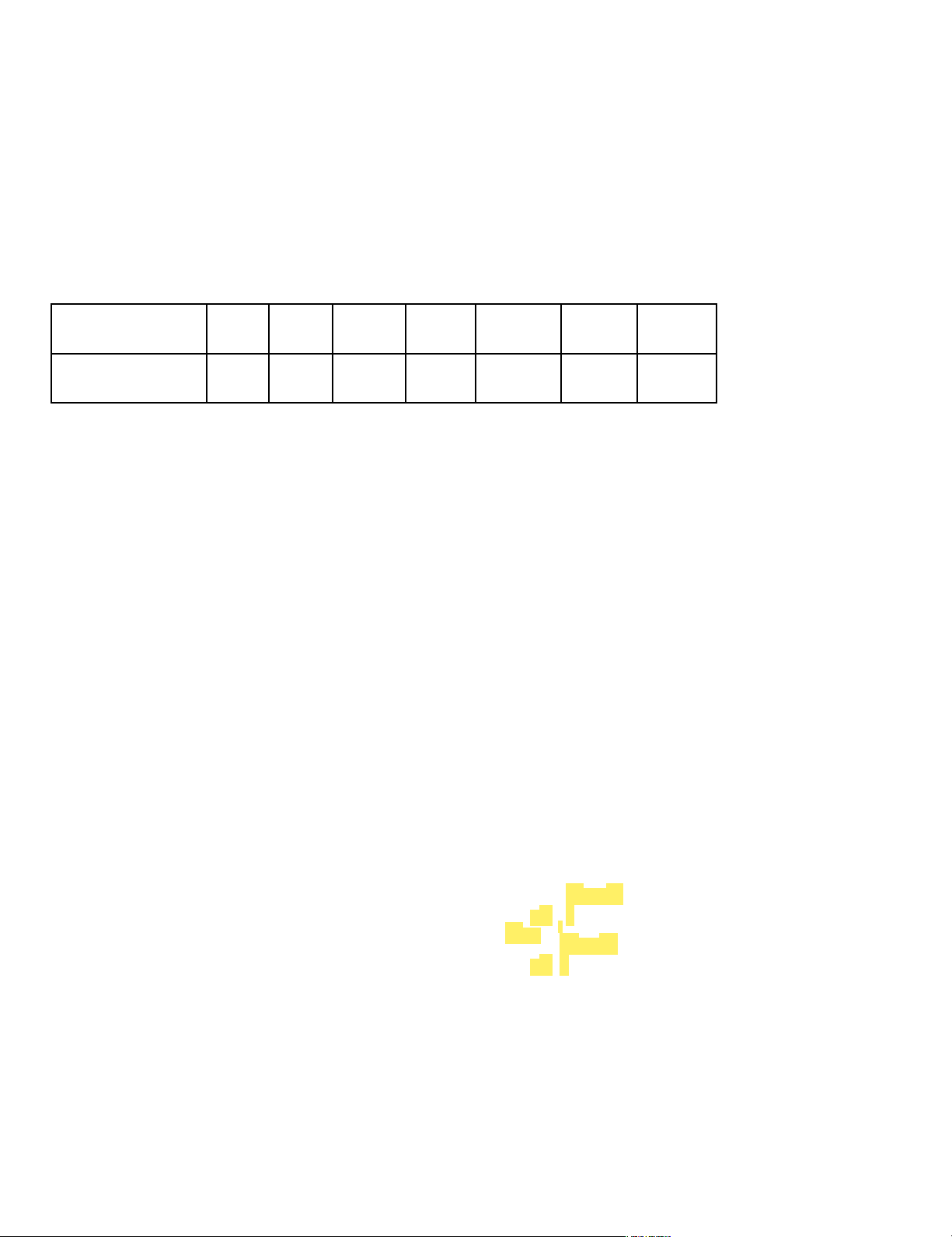
) và miền bác bỏ W để tiến hành kiểm được 0,99 qs 4,8 4 A. t
và W= (;2, 492) (2, 492;) qs . 25 0, 2 4,8 4 B. t qs
. 25 và W= (;2, 797) (2,797;) 0, 2 4 4,8 C. t
. 25 và W= (;2,797) (2,797;) qs 0, 2 4 4,8 D. t . 25 và W= (; 2,797) (2,797;) qs 0, 2
Câu 28: Thời gian bảo quản (đơn vị: ngày) của một loại sản phẩm Z là một biến ngẫu nhiên X với kỳ vọng là
. Theo số liệu cũ, thời gian bảo quản trung bình của loại sản phẩm này bằng 20 ngày. Để tăng thời gian bảo
quản trung bình lên, người ta đã thực hiện nhiều biện pháp bảo quản tân tiến. Sau một thời gian áp dụng các
biện pháp bảo quản mới, người ta kiểm tra ngẫu nhiên 225 sản phẩm và thu được thời gian bảo quan trung
bình bằng 28 ngày. Giả sử người kiểm tra muốn kiểm định với mức ý nghĩa 1%. Biết rằng (2,326) 0,99
và (2,576) 0,995 . Giả thuyết không H 0 , đối giả thuyết H và miền bác bỏ W để tiến hành kiểm định, được xác định như sau: H : H : A. 20 28 0
và W (2,326;) B. . 0
và W (2,326;)
H : 20
H : 28 H : H : C. 20 28 0
và W (2,326;) D. 0
và W (2,326;)
H : 20
H : 28
Câu 29: Đo ngẫu nhiên chiều cao (đơn vị: cm) của một số thanh niên trong khu vực A (có mật độ dân cư
rất đông), người ta thu được bảng dữ liệu sau; Chiều cao 161 163 165 167 169 171 173 Số cây 6 10 16 10 68 20 14
(1,96) (1,645)
, (2,326) 0,99 và (2,576) 0,995 . Với độ tin cậy Biết rằng 0,975 , 0,95 95%,
khoảng tin cậy đối xứng cho tỷ lệ thanh niên có chiều cao lớn hơn 168 cm là: A. (0,70833; 0,74208) B. (0,70833; 0,78257) C. (0,67459; 0,74208) D. (0,63409; 0,78257)
Câu 30: Đo ngẫu nhiên chiều cao (đơn vị: cm) của 144 cây thuộc một loại giống cây H được 1 tháng tuổi,
người ta thu được bảng dữ liệu sau; lOMoARcPSD|45315597 Chiều cao 14 14,2 14,4 14,6 14,8 15 15,2 Số cây 6 10 16 10 68 20 14
Biết rằng chiều cao của giống cây này được 1 tháng tuổi là một biến ngẫu nhiên có phân phối chuẩn và (1,645) ,(1,96) ,(2,326) 0,95 0,975 0,99
,(2,576) 0,995 . Với độ tin cậy 95%, khoảng tin cậy
đối xứng cho trung bình chiều cao của giống cây H được 1 tháng tuổi là: A. (14,6844; 14,7822) B. (14,7333; 14,7822) C. (14,694; 14,762) D. (14,6844; 14,7333)
Câu 31: Nhà máy H chuyên sản xuất một loại sản phẩm G. Một sản phẩm G được gọi là đạt chuẩn nếu trọng
lượng của nó thuộc khoảng (1,36; 1,62). Nhà máy H tuyên bố rằng tỷ lệ sản phẩm đạt tiểu chuẩn luôn là 80%.
Người ta nghi ngờ tỷ lệ này không đúng và nghĩ rằng nó thấp hơn. Cân ngẫu nhiên một số sản phẩm được
sản xuất bởi nhà máy H và thu được bảng số liệu sau: Trọng lượng (kg) 1 1,2 1,4 1,6 1,8 2 Số sản phẩm 22 66 160 120 22 10
Biết rằng (1,96) (1,645) , (2,326) 0,99
0,995 . Với mức ý nghĩa 5% , (2,576) 0,975 , 0,95 và
lựa chọn nào dưới đây là đúng. Trong đó p là tỷ lệ sản phẩm đạt chuẩn. : p 0, : p 0, H 8 H 8
và lời tuyên bố của nhà máy là sai A.
và lời tuyên bố của nhà máy là đúng 0 0 B.
H : p 0, 8
H : p 0, 8 0 : p 0,
và lời tuyên bố của nhà máy là sai C.
H 0 : p 0, 8 và lời tuyên bố của nhà máy là đúng H 8 H D. : p 0, 8
H : p 0, 8
Câu 32: Giả sử tuổi thọ của một loại pin A có phân phối chuẩn với kỳ vọng là . Theo như tuyên bố của hãng
sản xuất pin A đã công bố , tuổi thọ trung bình của mỗi quả pin A là 12 tháng. Nghi nghờ tuổi thọ trung bình
không còn như tuyên bố. Người ta kiểm tra ngẫu nhiên 25 quả pin thì tìm được tuổi thọ trung bình là 11,15 (25) (25) (24)
tháng và độ lệch mẫu hiệu chỉnh là 0,5 tháng. Biết rằng
T0,99 2, 485; T0,995 2, 787; T0,99 2, 492 và (24) T0,995 2, 797 .
Với mức ý nghĩa 1%, lựa chọn nào đúng? H 0 :12 A. và
lời tuyên bố của hãng sản xuất là sai 1 H : 2 H 0 :12 B. và
lời tuyên bố của hãng sản xuất là đúng H : 12 H 0 :12 C.
và lời tuyên bố của hãng sản xuất là sai H :12 H 0 :12 D.
và lời tuyên bố của nhà máy là đúng 1 H : 2 lOMoARcPSD|45315597
Câu 33: Trọng lượng của mỗi bao ngũ cốc loại A của một đại lý là một bi ến ngẫu nhiên có phân phối chuẩn
với kỳ vọng là . Đại lý tuyên bố rằng trọng lượng trung bình của mỗi bao ngũ cốc là 50 kg. Một người mua
hang nghi ngờ rằng trọng lượng trung bình của mỗi bao phải thấp hơn 50 kg. Người đó cân ngẫu nhiên 144 bao
ngũ cốc loại A và thu được trọng lượng trung bình của mỗi bao là 49,88 kg và độ lệch mẫu hiệu chỉnh là 2 kg.
Biết rằng (1,96) (1,645) 0,95 , (2,326)
và (2,576) 0,995 . Với mức ý nghĩa 5%, lựa 0,975 , 0,99
chọn nào dưới đây là đúng? H : A. 5 0 0
và lời tuyên bố của đại lý là sai.
H : 50 H :50 0 B.
và lời tuyên bố của đại lý là đúng H : 50 H0 :50 C.
và lời tuyên bố của đại lý là đúng H :50 H :50 0 D.
và lời tuyên bố của đại lý là sai H : 50
Câu 34: Có 6 hộp phấn loại 1 và 4 hộp phấn loại 2. Mỗi hộp phấn loại 1 gồm 16 viên phấn màu trắng và 4 viên
phấn màu vàng. Mỗi hộp phấn loại 2 gồm 15 viên phấn màu trắng và 5 viên phấn màu vàng. Lấy ngẫu nhiên một
hộp phấn và sau đó rút ngẫu nhiên một viên phấn từ hộp đã lấy. Xác suất để lấy được viên phấn màu trắng là A. 3 B. 12 C. 31 39 D. 10 15 40 50
Câu 35: Sản phẩm của nhà X được sản xuất bởi hai phân xưởng I và II. Tỷ lệ đóng góp sản phẩm trong tổng
sản phẩm được sản xuất bởi nhà máy của phân xưởng I và II lần lượt là 60% và 40%. Tỷ lệ sản phẩm không
đạt tiêu chuẩn do phân xưởng I và II sản xuất lần lượt là 2% và 3%. Lấy ngẫu nhiên một sản phẩm kiểm tra.
Xác suất để lấy được sản phẩm đạt tiêu chuẩn là A. 0,976 B. 0,588 C. 0,388 D. 0,975
Câu 36: Mệnh đề nào dưới đây là sai
A. Biến ngẫu nhiên là đại lượng lấy giá trị là một số thực bất kỳ. B.
với X là một biến ngẫu nhiên nào đó và là độ lệch chuẩn của X. 2
X (EX)2E( X X )
F (a) , ở đây X có thể là một biến ngẫu nhiên rời rạc hoặc liên tục và F(x) là hàm phân
C. P (a X b ) F
(b ) phối xác suất của X.
D. Nếu X N (a; 2 ) thì biến ngẫu nhiên X a có phân phối chuẩn tắc
Câu 37: Biến ngẫu nhiên liên tục X có hàm mật độ xác suất được cho bởi lOMoARcPSD|45315597 k (x[1, 2]) f 3
(x) x
( k là tham số). 0 (x[1, 2])
Phương sai của X bằng 16 8 A. .ln 2 8 8 16 D. 18 .ln 2 9 3 B. .l n 2 1 C. .ln 2 3 3 3 9
Câu 38: Lượng tiêu thụ năng lượng G của mỗi hộ gia đình tại khu vực A là một biến ngẫu nhiên X có
phân phối chuẩn với lượng tiêu thụ năng lượng trung bình là 80 (đơn vị năng lượng) và độ lệch chuẩn là
0,6 (đơn vị năng lượng). Xác suất để một hộ gia đình tại khu vực A có lượng tiêu thụ năng lượng trong
đoạn [79,7; 81,176] bằng A. Xấp xỉ 0,38 B. Xấp xỉ 0,975
C. Xấp xỉ 0,695
D. Xấp xỉ 0,67
Câu 39: Thực hiện tung một con xúc xắc đồng chất 20 lần liên tiếp và độc lập. Xác suất để tung được ít nhất
16 lần ra mặt 6 chấm biết rằng 15 lần tung đầu tiên đều ra mặt 6 chấm bằng: 11 4651 617 91 A. B. C. D. 36 7776 1296 216
Câu 40: Người ta cân ngẫu nhiên 200 quả trứng vịt trong một trang trại nuôi vịt và được số liệu sau:
Trọng lượng (gam) [50;52) [52;54) [54;56) [56;58) [58;60) [60;62) [62;64)
Số quả trứng 5 10 20 20 33 80 32 (1,645) (1,96)
Biết rằng trọng lượng của mỗi quả trứng vịt có phân phối chuẩn, 0,95 , 0,975 , (2,326) 0,99 (2,576) và 0,995
. Sử dụng mẫu đã cho, hỏi cần cân tối thiểu bao nhiêu quả trứng gà để
độ dài của khoảng tin cậy đối xứng (với độ tin cậy 95%) cho trọng lượng trung bình của mỗi quả trứng vịt
không vượt quá 0,2?
A. 3647 quả trứng vịt
B. 3646 quả trứng vịt
C. 3628 quả trứng vịt
D. 3629 quả trứng vịt
----------- HẾT ----------
Thí sinh được phép sử dụng bảng tra số liệu.Cán bộ coi thi không giải thích gì thêm.